华师大版数学八年级上册同步课时练习:14.2 勾股定理的应用(2课时、word、含答案)
文档属性
| 名称 | 华师大版数学八年级上册同步课时练习:14.2 勾股定理的应用(2课时、word、含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-18 21:03:50 | ||
图片预览




文档简介
14.2 第1课时 勾股定理在现实生活中的应用
知识点 利用勾股定理解决实际问题
1.如图果梯子的底端离建筑物9 m,那么15 m长的梯子可以到达建筑物的高度是( )
A.10 m B.11 m C.12 m D.13 m
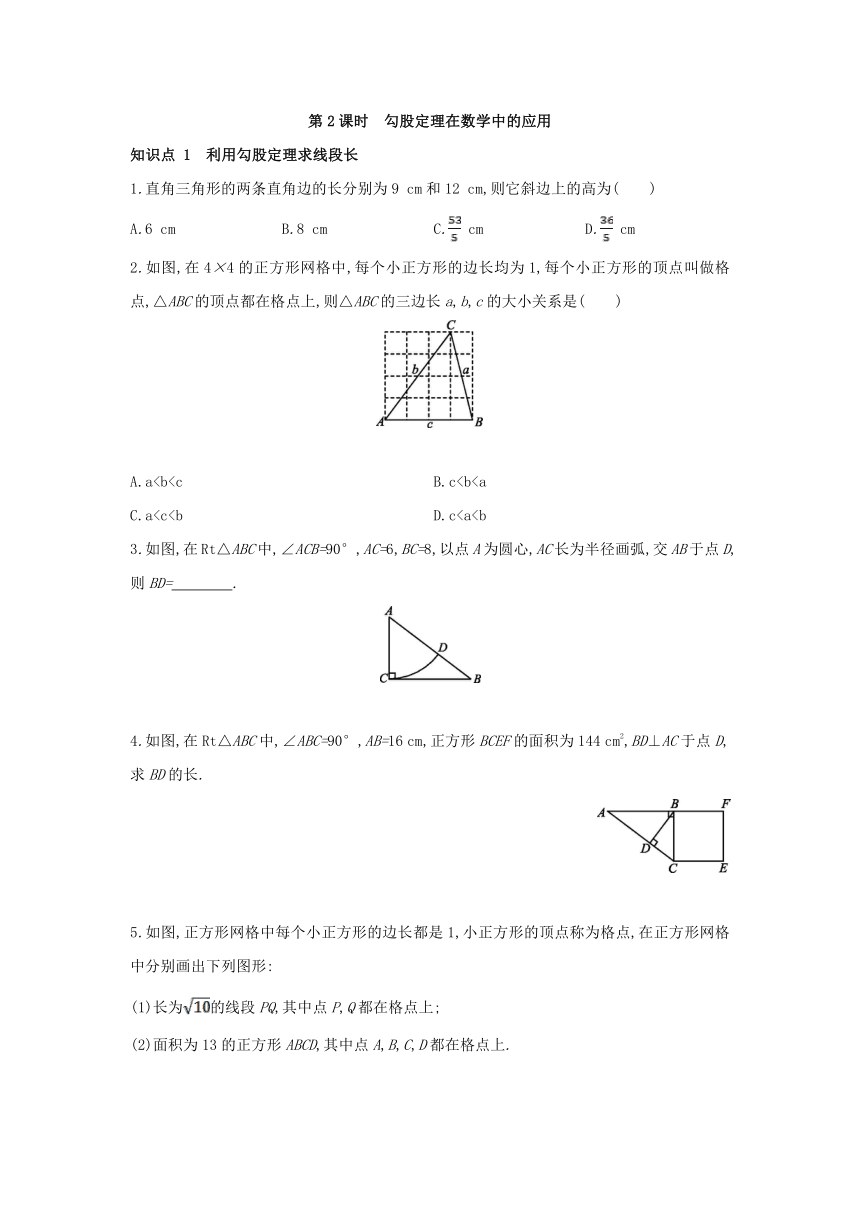
2.如图图,若圆柱的底面周长是30 cm,高是40 cm,从圆柱底部A处沿侧面缠绕一圈丝线到顶部B处做装饰,则这条丝线的最小长度是( )
A.80 cm B.70 cm
C.60 cm D.50 cm
3.《九章算术》是我国古代最重要的数学著作之一,在“勾股”章中记载了一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去本三尺,问折者高几何.”翻译成数学问题是:如图图所示,在△ABC中,∠ACB=90°,AC+AB=10,BC=3,求AC的长.若设AC=x,则可列方程为 .
4.如图图,一根12米高的电线杆AC两侧各用15米长的铁丝AB,AD固定(B,C,D三点共线),两个固定点B,D之间的距离是 米.
5.小东拿着一根长竹竿进一个宽 3米的长方形城门,他先横着拿,进不去,又竖起来拿,结果竿比城门高1米,当他把竹竿斜着拿时,两端正好顶着城门的对角,则竿长几米
6.假设小汽车在城市街道上的行驶速度不得超过70千米/时,如图图,一辆小汽车在一条城市街道上沿直线行驶,某一时刻刚好行驶到路面车速检测仪A的正前方30米的C处,过了2秒后,测得小汽车在与车速检测仪距离为50米的B处,那么这辆小汽车超速了吗
7.[教材练习第2题变式] 如图图,甲轮船以16海里/时的速度离开港口O向东南方向航行,乙轮船同时同地出发向西南方向航行.已知两船离开港口一个半小时后分别到达B,A两点,且AB=30海里,则乙轮船每小时航行多少海里
8.如图图,有两棵树,一棵高10米,另一棵高4米,两树相距8米(树的粗细忽略不计).一只小鸟从一棵树的树梢飞到另一棵树的树梢,则小鸟至少飞行( )
A.8米 B.10米 C.12米 D.14米
9.如图图所示,有一个由传感器控制的灯A,要装在门上方离地面4.5 m的墙上,任何东西只要移至距该灯5 m及5 m以内时,灯就会自动发光,则一个身高1.5 m的人走到离墙多远的地方灯刚好发光( )
A.4 m B.3 m C.5 m D.7 m
10.如图图所示,长方形零件上两孔中心A,B的距离约是 .(单位:cm,结果精确到个位)
11.如图图,一架2.5 m长的梯子斜靠在垂直于地面的墙AO上,这时AO为2 m.如图果梯子的顶端A沿墙下滑0.5 m,那么梯子的底端B向外移动 m.
12.如图是一块四边形木板,其中AB=16 cm,BC=24 cm,CD=9 cm,AD=25 cm,∠B=∠C=90°.李师傅找到BC边的中点P,连结AP,DP,发现△APD是直角三角形,请你通过计算说明理由.
13.如图,一个牧童在距小河南岸MN 4 km的A处牧马,而他正位于他的小屋B的西8 km、北7 km处,他想把他的马牵到小河边去饮水,然后回小屋,他要完成这件事情所走的最短路线的长为多少
14.如图,某沿海城市A接到台风警报,在该市正南方向120 km处有一台风中心正在B处形成,并沿着北偏东45°的方向以15 km/h的速度向点C移动.若在距台风中心150 km的区域内都将受到台风的影响,则
(1)画图计算说明:台风会影响到A市;
(2)画图计算说明:台风中心从B处出发后,经过几小时会影响到A市,对A市持续影响的时间是多少小时 经过几小时对A市的影响最大 [提示:(120)2=28800]
第2课时 勾股定理在数学中的应用
知识点 1 利用勾股定理求线段长
1.直角三角形的两条直角边的长分别为9 cm和12 cm,则它斜边上的高为( )
A.6 cm B.8 cm C. cm D. cm
2.如图,在4×4的正方形网格中,每个小正方形的边长均为1,每个小正方形的顶点叫做格点,△ABC的顶点都在格点上,则△ABC的三边长a,b,c的大小关系是( )
A.aC.a3.如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,以点A为圆心,AC长为半径画弧,交AB于点D,则BD= .
4.如图,在Rt△ABC中,∠ABC=90°,AB=16 cm,正方形BCEF的面积为144 cm2,BD⊥AC于点D,求BD的长.
5.如图,正方形网格中每个小正方形的边长都是1,小正方形的顶点称为格点,在正方形网格中分别画出下列图形:
(1)长为的线段PQ,其中点P,Q都在格点上;
(2)面积为13的正方形ABCD,其中点A,B,C,D都在格点上.
知识点 2 利用勾股定理求面积
6.在△ABC中,∠C=90°,AB=25,BC=24,则△ABC的面积等于 .
7.某市在“旧城改造”中计划在市内一块如图所示的三角形空地上种植某种草皮以美化环境.已知这种草皮每平方米售价a元,则购买这种草皮至少需要 元.
8.有一块四边形土地的形状如图所示,∠B=∠D=90°,AB=20米,BC=15米,CD=7米,计算这块土地的面积.
9.在Rt△ABC中,∠B=90°,BC=15,AC=17,以AB的长为直径作半圆,则此半圆的面积为( )
A.4π B.8π
C.16π D.以上都不对
10.如图所示,在Rt△ABC中,∠C=90°,AB=10 cm,BC=8 cm,BD平分∠ABC交AC于点D,DE⊥AB,垂足为E,则DE= cm.
11.如图,已知在△ABC中,∠ABC=90°,AB=BC,三角形的顶点分别在相互平行的三条直线l1,l2,l3上,且相邻两平行线之间的距离均为1,则AC的长是 .
12.如图,已知等腰直角三角形ABC的直角边长为1,以△ABC的斜边为直角边,画第二个等腰直角三角形ACD,再以△ACD的斜边为直角边,画第三个等腰直角三角形ADE……依次类推,直到第五个等腰直角三角形AFG.求由这五个等腰直角三角形所构成的图形的面积.
13.如图,已知△ABC中,∠B=90°,AB=16 cm,BC=12 cm,P,Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为1 cm/s,点Q从点B开始沿B→C→A方向运动,且速度为2 cm/s,两点同时出发,设运动的时间为t s.
(1)出发2 s后,求PQ的长;
(2)当点Q在边BC上运动时,出发几秒后,△PQB是等腰三角形
(3)当点Q在边CA上运动时,求能使△BCQ是等腰三角形的运动时间.
答案
生活中的应用
1.C 先构造直角三角形模型,然后利用勾股定理,在直角三角形中已知斜边和一条直角边求另一条直角边.
2.D 如图图,把圆柱的侧面展开,得到长方形ACBD,则从圆柱底部A处沿侧面缠绕一圈丝线到顶部B处做装饰,这条丝线的最小长度是长方形的对角线AB的长.
∵圆柱的底面周长是30 cm,高是40 cm,
∴AB===50(cm).
故选D.
3.x2+32=(10-x)2 已知AC=x,则AB=10-x,再根据勾股定理即可得出结论.
∵AC=x,AC+AB=10,∴AB=10-x.
∵在△ABC中,∠ACB=90°,
∴AC2+BC2=AB2,即x2+32=(10-x)2.
故答案为x2+32=(10-x)2.
4.18
5.解:设竿长x米,则城门高(x-1)米.
根据题意列方程,得(x-1)2+32=x2,
解得x=5.
答:竿长5米.
6.解:根据题意,得AC=30米,AB=50米,∠C=90°.
在Rt△ACB中,根据勾股定理,得BC===40(米),
小汽车2秒行驶了40米,则1小时行驶40×30×60=72000(米),
即小汽车的行驶速度为72千米/时.
因为72>70,所以这辆小汽车超速了.
7.解:∵甲轮船向东南方向航行,乙轮船向西南方向航行,∴AO⊥BO.
∵甲轮船以16海里/时的速度航行了一个半小时,∴BO=16×1.5=24(海里).
又∵AB=30海里,∴在Rt△AOB中,AO===18(海里),
∴乙轮船每小时航行18÷1.5=12(海里).
8.B
9.A 如图图.由题意可知,BE=CD=1.5 m,AE=AB-BE=4.5-1.5=3(m),AC=5 m.
由勾股定理,得CE==4(m),
故该人走到离墙4 m远的地方灯刚好发光.
故选A.
10.67 cm 分别过A,B两点作长方形长和宽的垂线并交于点C,构造Rt△ABC,利用勾股定理,得AB2=AC2+BC2=192+642=4457,AB≈67(cm).
11.0.5 ∵Rt△OAB中,AB=2.5 m,AO=2 m,
∴OB===1.5(m);
同理,Rt△OCD中,
∵CD=2.5 m,OC=2-0.5=1.5(m),
∴OD===2(m),
∴BD=OD-OB=2-1.5=0.5(m).
故答案为0.5.
12.解:∵P为BC的中点,
∴BP=CP=BC=12(cm).
在Rt△ABP中,根据勾股定理可得:AB2+BP2=AP2,
即162+122=AP2,解得AP=20(cm).
同理可得:DP=15(cm).
∵152+202=252,∴DP2+AP2=AD2,
∴△APD是直角三角形.
13.解:如图图,
作点A关于MN的对称点A',连结A'B交MN于点P,则AP+PB就是最短路线.
∵A'P=AP,
∴AP+PB=A'P+PB=A'B.
∵AC=7 km,AA'=2×4=8(km),
∴A'C=AA'+AC=15 km.
在Rt△A'CB中,根据勾股定理,得
A'B===17(km).
故他要完成这件事情所走的最短路线的长为17 km.
14.解:(1)如图图,过点A作AD⊥BC于点D.
由题意得∠B=45°,
∴∠BAD=45°,则AD=BD.
∵AD2+BD2=AB2=(120)2,
∴AD=BD=120 km<150 km,
∴台风会影响到A市.
(2)如图图,在BC上取两点E,F,使AE=AF=150 km.
在Rt△ADE中,
DE===90(km),
∴BE=120-90=30(km).
∵=2(h),=12(h),=8(h),
∴台风中心从B处出发后,经过2 h会影响到A市,对A市持续影响的时间是12 h,经过8 h对A市的影响最大.
答案
1.D 根据题意,画出图形,结合题中已知条件求解.
∵在Rt△ABC中,AC=9 cm,BC=12 cm,
∴AB=15 cm.
如图图,过点C作CD⊥AB于点D.
∵S△ABC=AC·BC=CD·AB,
∴×9×12=×15×CD,∴CD=(cm).
故选D.
2.D 由勾股定理可得a==,b==5.
又∵c=4,∴c3.4
4. 由正方形BCEF的面积可求BC的长,又知AB可求AC,因此可由面积求出斜边上的高BD.
解:∵S正方形BCEF=144 cm2,
即BC2=144 cm2,
∴BC=12 cm.
在Rt△ABC中,由勾股定理,得
AC===20(cm).
∵S△ABC=AC·BD=AB·BC,
即×20×BD=×16×12,
∴BD=9.6(cm).
5. (1)由勾股定理可知当直角边长分别为1和3时,斜边长为,由此可得线段PQ;
(2)由勾股定理可知当直角边长分别为2和3时,斜边长为,把斜边长作为正方形的边长即可得到面积为13的正方形ABCD.
解:(1)(2)如图图所示(所画的线段PQ、正方形ABCD的形状、大小相同,位置可能不同):
6.84
7.60a 先求出该三角形空地的面积,由已知三边长,可判断此三角形为直角三角形,用两条直角边的乘积的一半可求出其面积.
8.解:如图图,连结AC,将四边形ABCD分割成两个三角形,其面积为两个三角形的面积之和.
在Rt△ABC中,AC为斜边,
则AC===25(米).
在Rt△ACD中,AC为斜边,
则AD===24(米).
故四边形ABCD的面积=AB·BC+AD·CD=234(米2).
答:这块土地的面积为234平方米.
9.B 在Rt△ABC中,AB2=AC2-BC2=172-152=82,∴AB=8,
∴S半圆=πR2=π×2=8π.
10. 在Rt△ABC中,∠C=90°,AB=10 cm,BC=8 cm,
则由勾股定理得AC===6(cm).
∵BD平分∠ABC,DE⊥AB,DC⊥BC,
∴DE=DC.
在Rt△BDC和Rt△BDE中,
∵BD=BD,DC=DE,
∴Rt△BDC≌Rt△BDE,
∴BC=BE.
∵BC=8 cm,∴BE=8 cm,∴AE=2 cm.
设DE=DC=x cm,则AD=(6-x)cm.
在Rt△ADE中,由勾股定理,得AD2=AE2+ED2,即(6-x)2=22+x2,解得x=,
即DE= cm.
故答案是.
11. 如图图,过点A作AD⊥l3于点D,过点C作CE⊥l3于点E.
∵∠ABC=90°,
∴∠ABD+∠CBE=90°.
又∵∠BAD+∠ABD=90°,
∴∠BAD=∠CBE.
又∵AB=BC,∠ADB=∠BEC=90°,
∴△ABD≌△BCE,
∴AD=BE=1.
在Rt△BCE中,根据勾股定理,得BC==.
在Rt△ABC中,根据勾股定理,得AC==.
12.解:第一个等腰直角三角形的面积为×12=,第二个等腰直角三角形的面积为×()2=1,第三个等腰直角三角形的面积为×22=2,第四个等腰直角三角形的面积为×()2=4,第五个等腰直角三角形的面积为×42=8,所以由这五个等腰直角三角形所构成的图形的面积为.
13.解:(1)∵BQ=2×2=4(cm),BP=AB-AP=16-2×1=14(cm),∠B=90°,
∴PQ==(cm).
(2)当点Q在边BC上运动时,若△PQB是等腰三角形,则BQ=BP.由题意,得BQ=2t cm,BP=(16-t)cm,∴2t=16-t,解得t=,
即当点Q在边BC上运动时,出发 s后,△PQB是等腰三角形.
(3)①若CQ=BQ,如图图(a)所示,
则∠C=∠CBQ.
∵∠ABC=90°,
∴∠CBQ+∠ABQ=90°,
∠A+∠C=90°,
∴∠A=∠ABQ,
∴BQ=AQ,
∴CQ=AQ.
在Rt△ABC中,由勾股定理,得AC==20(cm),
∴CQ=AQ=10(cm),
则BC+CQ=22(cm),
∴t=22÷2=11.
②若CQ=BC,如图图(b)所示,
则BC+CQ=24(cm),
∴t=24÷2=12.
③若BC=BQ,如图图(c)所示.
过点B作BE⊥AC于点E,
则BE===(cm),
∴CE===(cm).
∵BC=BQ,BE⊥CQ,∴CQ=2CE=14.4(cm),
则BC+CQ=26.4(cm),
∴t=26.4÷2=13.2.
综上所述,当运动时间为11 s或12 s或13.2 s时,△BCQ是等腰三角形.
知识点 利用勾股定理解决实际问题
1.如图果梯子的底端离建筑物9 m,那么15 m长的梯子可以到达建筑物的高度是( )
A.10 m B.11 m C.12 m D.13 m
2.如图图,若圆柱的底面周长是30 cm,高是40 cm,从圆柱底部A处沿侧面缠绕一圈丝线到顶部B处做装饰,则这条丝线的最小长度是( )
A.80 cm B.70 cm
C.60 cm D.50 cm
3.《九章算术》是我国古代最重要的数学著作之一,在“勾股”章中记载了一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去本三尺,问折者高几何.”翻译成数学问题是:如图图所示,在△ABC中,∠ACB=90°,AC+AB=10,BC=3,求AC的长.若设AC=x,则可列方程为 .
4.如图图,一根12米高的电线杆AC两侧各用15米长的铁丝AB,AD固定(B,C,D三点共线),两个固定点B,D之间的距离是 米.
5.小东拿着一根长竹竿进一个宽 3米的长方形城门,他先横着拿,进不去,又竖起来拿,结果竿比城门高1米,当他把竹竿斜着拿时,两端正好顶着城门的对角,则竿长几米
6.假设小汽车在城市街道上的行驶速度不得超过70千米/时,如图图,一辆小汽车在一条城市街道上沿直线行驶,某一时刻刚好行驶到路面车速检测仪A的正前方30米的C处,过了2秒后,测得小汽车在与车速检测仪距离为50米的B处,那么这辆小汽车超速了吗
7.[教材练习第2题变式] 如图图,甲轮船以16海里/时的速度离开港口O向东南方向航行,乙轮船同时同地出发向西南方向航行.已知两船离开港口一个半小时后分别到达B,A两点,且AB=30海里,则乙轮船每小时航行多少海里
8.如图图,有两棵树,一棵高10米,另一棵高4米,两树相距8米(树的粗细忽略不计).一只小鸟从一棵树的树梢飞到另一棵树的树梢,则小鸟至少飞行( )
A.8米 B.10米 C.12米 D.14米
9.如图图所示,有一个由传感器控制的灯A,要装在门上方离地面4.5 m的墙上,任何东西只要移至距该灯5 m及5 m以内时,灯就会自动发光,则一个身高1.5 m的人走到离墙多远的地方灯刚好发光( )
A.4 m B.3 m C.5 m D.7 m
10.如图图所示,长方形零件上两孔中心A,B的距离约是 .(单位:cm,结果精确到个位)
11.如图图,一架2.5 m长的梯子斜靠在垂直于地面的墙AO上,这时AO为2 m.如图果梯子的顶端A沿墙下滑0.5 m,那么梯子的底端B向外移动 m.
12.如图是一块四边形木板,其中AB=16 cm,BC=24 cm,CD=9 cm,AD=25 cm,∠B=∠C=90°.李师傅找到BC边的中点P,连结AP,DP,发现△APD是直角三角形,请你通过计算说明理由.
13.如图,一个牧童在距小河南岸MN 4 km的A处牧马,而他正位于他的小屋B的西8 km、北7 km处,他想把他的马牵到小河边去饮水,然后回小屋,他要完成这件事情所走的最短路线的长为多少
14.如图,某沿海城市A接到台风警报,在该市正南方向120 km处有一台风中心正在B处形成,并沿着北偏东45°的方向以15 km/h的速度向点C移动.若在距台风中心150 km的区域内都将受到台风的影响,则
(1)画图计算说明:台风会影响到A市;
(2)画图计算说明:台风中心从B处出发后,经过几小时会影响到A市,对A市持续影响的时间是多少小时 经过几小时对A市的影响最大 [提示:(120)2=28800]
第2课时 勾股定理在数学中的应用
知识点 1 利用勾股定理求线段长
1.直角三角形的两条直角边的长分别为9 cm和12 cm,则它斜边上的高为( )
A.6 cm B.8 cm C. cm D. cm
2.如图,在4×4的正方形网格中,每个小正方形的边长均为1,每个小正方形的顶点叫做格点,△ABC的顶点都在格点上,则△ABC的三边长a,b,c的大小关系是( )
A.a
4.如图,在Rt△ABC中,∠ABC=90°,AB=16 cm,正方形BCEF的面积为144 cm2,BD⊥AC于点D,求BD的长.
5.如图,正方形网格中每个小正方形的边长都是1,小正方形的顶点称为格点,在正方形网格中分别画出下列图形:
(1)长为的线段PQ,其中点P,Q都在格点上;
(2)面积为13的正方形ABCD,其中点A,B,C,D都在格点上.
知识点 2 利用勾股定理求面积
6.在△ABC中,∠C=90°,AB=25,BC=24,则△ABC的面积等于 .
7.某市在“旧城改造”中计划在市内一块如图所示的三角形空地上种植某种草皮以美化环境.已知这种草皮每平方米售价a元,则购买这种草皮至少需要 元.
8.有一块四边形土地的形状如图所示,∠B=∠D=90°,AB=20米,BC=15米,CD=7米,计算这块土地的面积.
9.在Rt△ABC中,∠B=90°,BC=15,AC=17,以AB的长为直径作半圆,则此半圆的面积为( )
A.4π B.8π
C.16π D.以上都不对
10.如图所示,在Rt△ABC中,∠C=90°,AB=10 cm,BC=8 cm,BD平分∠ABC交AC于点D,DE⊥AB,垂足为E,则DE= cm.
11.如图,已知在△ABC中,∠ABC=90°,AB=BC,三角形的顶点分别在相互平行的三条直线l1,l2,l3上,且相邻两平行线之间的距离均为1,则AC的长是 .
12.如图,已知等腰直角三角形ABC的直角边长为1,以△ABC的斜边为直角边,画第二个等腰直角三角形ACD,再以△ACD的斜边为直角边,画第三个等腰直角三角形ADE……依次类推,直到第五个等腰直角三角形AFG.求由这五个等腰直角三角形所构成的图形的面积.
13.如图,已知△ABC中,∠B=90°,AB=16 cm,BC=12 cm,P,Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为1 cm/s,点Q从点B开始沿B→C→A方向运动,且速度为2 cm/s,两点同时出发,设运动的时间为t s.
(1)出发2 s后,求PQ的长;
(2)当点Q在边BC上运动时,出发几秒后,△PQB是等腰三角形
(3)当点Q在边CA上运动时,求能使△BCQ是等腰三角形的运动时间.
答案
生活中的应用
1.C 先构造直角三角形模型,然后利用勾股定理,在直角三角形中已知斜边和一条直角边求另一条直角边.
2.D 如图图,把圆柱的侧面展开,得到长方形ACBD,则从圆柱底部A处沿侧面缠绕一圈丝线到顶部B处做装饰,这条丝线的最小长度是长方形的对角线AB的长.
∵圆柱的底面周长是30 cm,高是40 cm,
∴AB===50(cm).
故选D.
3.x2+32=(10-x)2 已知AC=x,则AB=10-x,再根据勾股定理即可得出结论.
∵AC=x,AC+AB=10,∴AB=10-x.
∵在△ABC中,∠ACB=90°,
∴AC2+BC2=AB2,即x2+32=(10-x)2.
故答案为x2+32=(10-x)2.
4.18
5.解:设竿长x米,则城门高(x-1)米.
根据题意列方程,得(x-1)2+32=x2,
解得x=5.
答:竿长5米.
6.解:根据题意,得AC=30米,AB=50米,∠C=90°.
在Rt△ACB中,根据勾股定理,得BC===40(米),
小汽车2秒行驶了40米,则1小时行驶40×30×60=72000(米),
即小汽车的行驶速度为72千米/时.
因为72>70,所以这辆小汽车超速了.
7.解:∵甲轮船向东南方向航行,乙轮船向西南方向航行,∴AO⊥BO.
∵甲轮船以16海里/时的速度航行了一个半小时,∴BO=16×1.5=24(海里).
又∵AB=30海里,∴在Rt△AOB中,AO===18(海里),
∴乙轮船每小时航行18÷1.5=12(海里).
8.B
9.A 如图图.由题意可知,BE=CD=1.5 m,AE=AB-BE=4.5-1.5=3(m),AC=5 m.
由勾股定理,得CE==4(m),
故该人走到离墙4 m远的地方灯刚好发光.
故选A.
10.67 cm 分别过A,B两点作长方形长和宽的垂线并交于点C,构造Rt△ABC,利用勾股定理,得AB2=AC2+BC2=192+642=4457,AB≈67(cm).
11.0.5 ∵Rt△OAB中,AB=2.5 m,AO=2 m,
∴OB===1.5(m);
同理,Rt△OCD中,
∵CD=2.5 m,OC=2-0.5=1.5(m),
∴OD===2(m),
∴BD=OD-OB=2-1.5=0.5(m).
故答案为0.5.
12.解:∵P为BC的中点,
∴BP=CP=BC=12(cm).
在Rt△ABP中,根据勾股定理可得:AB2+BP2=AP2,
即162+122=AP2,解得AP=20(cm).
同理可得:DP=15(cm).
∵152+202=252,∴DP2+AP2=AD2,
∴△APD是直角三角形.
13.解:如图图,
作点A关于MN的对称点A',连结A'B交MN于点P,则AP+PB就是最短路线.
∵A'P=AP,
∴AP+PB=A'P+PB=A'B.
∵AC=7 km,AA'=2×4=8(km),
∴A'C=AA'+AC=15 km.
在Rt△A'CB中,根据勾股定理,得
A'B===17(km).
故他要完成这件事情所走的最短路线的长为17 km.
14.解:(1)如图图,过点A作AD⊥BC于点D.
由题意得∠B=45°,
∴∠BAD=45°,则AD=BD.
∵AD2+BD2=AB2=(120)2,
∴AD=BD=120 km<150 km,
∴台风会影响到A市.
(2)如图图,在BC上取两点E,F,使AE=AF=150 km.
在Rt△ADE中,
DE===90(km),
∴BE=120-90=30(km).
∵=2(h),=12(h),=8(h),
∴台风中心从B处出发后,经过2 h会影响到A市,对A市持续影响的时间是12 h,经过8 h对A市的影响最大.
答案
1.D 根据题意,画出图形,结合题中已知条件求解.
∵在Rt△ABC中,AC=9 cm,BC=12 cm,
∴AB=15 cm.
如图图,过点C作CD⊥AB于点D.
∵S△ABC=AC·BC=CD·AB,
∴×9×12=×15×CD,∴CD=(cm).
故选D.
2.D 由勾股定理可得a==,b==5.
又∵c=4,∴c
4. 由正方形BCEF的面积可求BC的长,又知AB可求AC,因此可由面积求出斜边上的高BD.
解:∵S正方形BCEF=144 cm2,
即BC2=144 cm2,
∴BC=12 cm.
在Rt△ABC中,由勾股定理,得
AC===20(cm).
∵S△ABC=AC·BD=AB·BC,
即×20×BD=×16×12,
∴BD=9.6(cm).
5. (1)由勾股定理可知当直角边长分别为1和3时,斜边长为,由此可得线段PQ;
(2)由勾股定理可知当直角边长分别为2和3时,斜边长为,把斜边长作为正方形的边长即可得到面积为13的正方形ABCD.
解:(1)(2)如图图所示(所画的线段PQ、正方形ABCD的形状、大小相同,位置可能不同):
6.84
7.60a 先求出该三角形空地的面积,由已知三边长,可判断此三角形为直角三角形,用两条直角边的乘积的一半可求出其面积.
8.解:如图图,连结AC,将四边形ABCD分割成两个三角形,其面积为两个三角形的面积之和.
在Rt△ABC中,AC为斜边,
则AC===25(米).
在Rt△ACD中,AC为斜边,
则AD===24(米).
故四边形ABCD的面积=AB·BC+AD·CD=234(米2).
答:这块土地的面积为234平方米.
9.B 在Rt△ABC中,AB2=AC2-BC2=172-152=82,∴AB=8,
∴S半圆=πR2=π×2=8π.
10. 在Rt△ABC中,∠C=90°,AB=10 cm,BC=8 cm,
则由勾股定理得AC===6(cm).
∵BD平分∠ABC,DE⊥AB,DC⊥BC,
∴DE=DC.
在Rt△BDC和Rt△BDE中,
∵BD=BD,DC=DE,
∴Rt△BDC≌Rt△BDE,
∴BC=BE.
∵BC=8 cm,∴BE=8 cm,∴AE=2 cm.
设DE=DC=x cm,则AD=(6-x)cm.
在Rt△ADE中,由勾股定理,得AD2=AE2+ED2,即(6-x)2=22+x2,解得x=,
即DE= cm.
故答案是.
11. 如图图,过点A作AD⊥l3于点D,过点C作CE⊥l3于点E.
∵∠ABC=90°,
∴∠ABD+∠CBE=90°.
又∵∠BAD+∠ABD=90°,
∴∠BAD=∠CBE.
又∵AB=BC,∠ADB=∠BEC=90°,
∴△ABD≌△BCE,
∴AD=BE=1.
在Rt△BCE中,根据勾股定理,得BC==.
在Rt△ABC中,根据勾股定理,得AC==.
12.解:第一个等腰直角三角形的面积为×12=,第二个等腰直角三角形的面积为×()2=1,第三个等腰直角三角形的面积为×22=2,第四个等腰直角三角形的面积为×()2=4,第五个等腰直角三角形的面积为×42=8,所以由这五个等腰直角三角形所构成的图形的面积为.
13.解:(1)∵BQ=2×2=4(cm),BP=AB-AP=16-2×1=14(cm),∠B=90°,
∴PQ==(cm).
(2)当点Q在边BC上运动时,若△PQB是等腰三角形,则BQ=BP.由题意,得BQ=2t cm,BP=(16-t)cm,∴2t=16-t,解得t=,
即当点Q在边BC上运动时,出发 s后,△PQB是等腰三角形.
(3)①若CQ=BQ,如图图(a)所示,
则∠C=∠CBQ.
∵∠ABC=90°,
∴∠CBQ+∠ABQ=90°,
∠A+∠C=90°,
∴∠A=∠ABQ,
∴BQ=AQ,
∴CQ=AQ.
在Rt△ABC中,由勾股定理,得AC==20(cm),
∴CQ=AQ=10(cm),
则BC+CQ=22(cm),
∴t=22÷2=11.
②若CQ=BC,如图图(b)所示,
则BC+CQ=24(cm),
∴t=24÷2=12.
③若BC=BQ,如图图(c)所示.
过点B作BE⊥AC于点E,
则BE===(cm),
∴CE===(cm).
∵BC=BQ,BE⊥CQ,∴CQ=2CE=14.4(cm),
则BC+CQ=26.4(cm),
∴t=26.4÷2=13.2.
综上所述,当运动时间为11 s或12 s或13.2 s时,△BCQ是等腰三角形.
