2021-2022学年高二下学期数学人教A版(2019)选择性必修第三册7.1.1条件概率课件(共12张PPT)
文档属性
| 名称 | 2021-2022学年高二下学期数学人教A版(2019)选择性必修第三册7.1.1条件概率课件(共12张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 658.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-18 10:25:40 | ||
图片预览




文档简介
(共12张PPT)
高二数学选择性必修第三册
第七章:随机变量及其分布
7.1.1 条件概率
1.了解条件概率的概念,能计算简单随机事件的条件概率.
2.会利用乘法公式计算概率.
一、学习目标(1分钟)
二、问题导学(3分钟)
样本空间的样本点只有有限个
每个样本点发生的可能性相等
如果事件 和 不独立,
如何表示积事件 的概率呢?
事件A与B相互独立的定义:
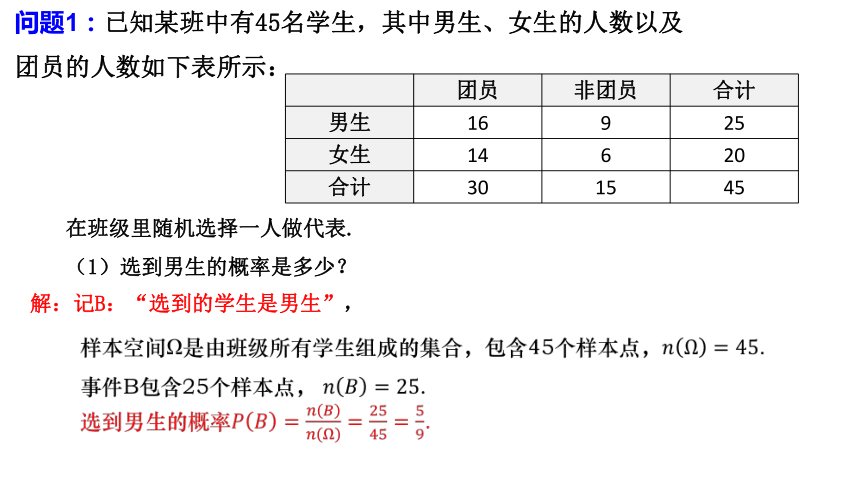
问题1:某个班级有45名学生,其中男生、女生的人数及团员的人数如下表所示:
团员 非团员 合计
男生 16 9 25
女生 14 6 20
合计 30 15 45
在班级里随机选择一人做代表:
(1)选到男生的概率是多少?
(2)如果已知选到的是团员,那么选到的是男生的概率是多少?
三、点拨精讲(28分钟)
班级所以学生组成的集合
样本空间为:
样本空间为:
班级所有团员组成的集合
在班级里随机选择一人做代表.
(1)选到男生的概率是多少?
团员 非团员 合计
男生 16 9 25
女生 14 6 20
合计 30 15 45
解:记B:“选到的学生是男生”,
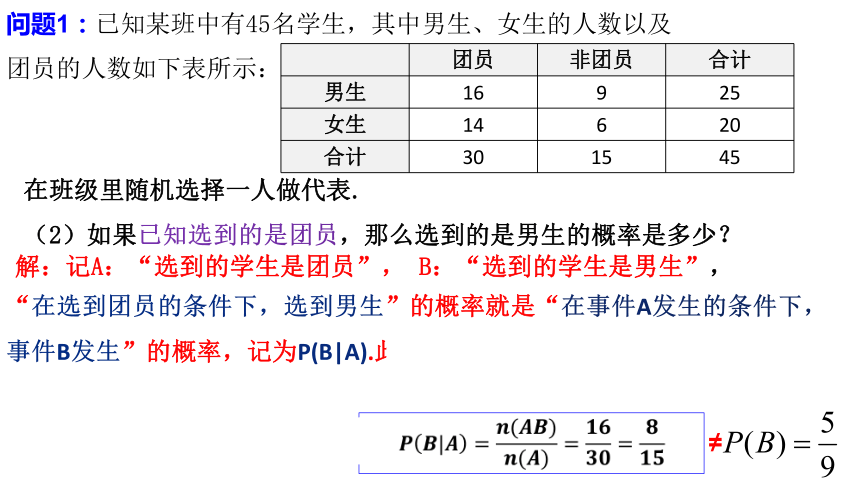
问题1:已知某班中有45名学生,其中男生、女生的人数以及团员的人数如下表所示:
在班级里随机选择一人做代表.
(2)如果已知选到的是团员,那么选到的是男生的概率是多少?
团员 非团员 合计
男生 16 9 25
女生 14 6 20
合计 30 15 45
问题1:已知某班中有45名学生,其中男生、女生的人数以及团员的人数如下表所示:
“在选到团员的条件下,选到男生”的概率就是“在事件A发生的条件下,事件B发生”的概率,记为P(B|A).此时相当于以A为样本空间来考虑事件B发生的概率,而在新的样本空间中事件B就是积事件AB,包含的样本点数n(AB)=16.根据古典概型知识可知,
解:记A:“选到的学生是团员”, B:“选到的学生是男生”,
≠
问题2:假定生男孩和生女孩是等可能的,某个家庭有2个孩子,问:
(1)两个孩子都是女孩的概率?
(2)如果有1个孩子是女孩,那么两个孩子都是女孩的概率又是多少?
所以
(1)设 =“有1个孩子是女孩”, =“2个孩子都是女孩”.
(2)“如果有1个孩子是女孩,两个孩子都是女孩”的概率就是“在事件 发生的条件下,事件 发生”的概率,记为
大 小
大 小
大 小
大 小
解:
≠P(B)
样本空间:任何性别的两个孩子的所有组合
样本空间:有1个女孩的两个孩子的所有组合
求 的一般思想:
AB
A
B
W
1、若已知事件 A 发生,则只需在 A发生的范围内考虑问题,即样本空间为A .
2、在事件A 发生的情况下事件B发生,等价于在样本空间为A的范围内,事件A和事件B同时发生.
所以事件 发生的条件下,事件 发生的概率
读作:在A发生的条件下B发生的概率.
条件概率定义:
一般地,设A,B为两个随机事件,且P(A)>0,我们称
为在事件A发生的条件下,事件B发生的条件概率.
简称条件概率.
P(AB)=P(A)P(B|A).
对任意两个事件A与B,若P(A)>0,则 P(AB)=P(A)P(B|A).
我们称上式为概率的乘法公式
例1 在5道试题中有3道代数题和2道几何题,每次从中随机抽出1道题,抽出的题不再放回. 求:
(1) 第1次抽到代数题且第2次抽到几何题的概率;
(2) 在第1次抽到代数题的条件下,第2次抽到几何题的概率.
(代1,几1)
(代1,几2)
(代2,几1)
(代2,几2)
(代3,几1)
(代3,几2)
(代1,代2)
(代1,代3)
(代2,代1)
(代2,代3)
(代3,代1)
(代3,代2)
(几1,代1)
(几1,代2)
(几1,代3)
(几1,几2)
(几2,代1)
(几2,代2)
(几2,代3)
(几2,几1)
2.概率乘法公式
1.条件概率公式:
3.求条件概率方法
方法一:条件概率定义法;
方法二:缩小样本空间法;
四、课堂小结(1分钟)
1.某地区空气质量监测资料表明,一天的空气质量为优良的概率是0.75,连续两天的空气质量为优良的概率是0.6,已知某天的空气质量为优良,则随后一天的空气质量为优良的概率是 ( )
A.0.8 B.0.75 C.0.6 D.0.45
A
五、当堂检测(12分钟)
2.一个盒子中有6个白球,4个黑球,从中不放回地每次任取1只,连取2次,则第一次取得白球的概率是________,已知第一次取得白球,那么第二次取得白球的概率是________
高二数学选择性必修第三册
第七章:随机变量及其分布
7.1.1 条件概率
1.了解条件概率的概念,能计算简单随机事件的条件概率.
2.会利用乘法公式计算概率.
一、学习目标(1分钟)
二、问题导学(3分钟)
样本空间的样本点只有有限个
每个样本点发生的可能性相等
如果事件 和 不独立,
如何表示积事件 的概率呢?
事件A与B相互独立的定义:
问题1:某个班级有45名学生,其中男生、女生的人数及团员的人数如下表所示:
团员 非团员 合计
男生 16 9 25
女生 14 6 20
合计 30 15 45
在班级里随机选择一人做代表:
(1)选到男生的概率是多少?
(2)如果已知选到的是团员,那么选到的是男生的概率是多少?
三、点拨精讲(28分钟)
班级所以学生组成的集合
样本空间为:
样本空间为:
班级所有团员组成的集合
在班级里随机选择一人做代表.
(1)选到男生的概率是多少?
团员 非团员 合计
男生 16 9 25
女生 14 6 20
合计 30 15 45
解:记B:“选到的学生是男生”,
问题1:已知某班中有45名学生,其中男生、女生的人数以及团员的人数如下表所示:
在班级里随机选择一人做代表.
(2)如果已知选到的是团员,那么选到的是男生的概率是多少?
团员 非团员 合计
男生 16 9 25
女生 14 6 20
合计 30 15 45
问题1:已知某班中有45名学生,其中男生、女生的人数以及团员的人数如下表所示:
“在选到团员的条件下,选到男生”的概率就是“在事件A发生的条件下,事件B发生”的概率,记为P(B|A).此时相当于以A为样本空间来考虑事件B发生的概率,而在新的样本空间中事件B就是积事件AB,包含的样本点数n(AB)=16.根据古典概型知识可知,
解:记A:“选到的学生是团员”, B:“选到的学生是男生”,
≠
问题2:假定生男孩和生女孩是等可能的,某个家庭有2个孩子,问:
(1)两个孩子都是女孩的概率?
(2)如果有1个孩子是女孩,那么两个孩子都是女孩的概率又是多少?
所以
(1)设 =“有1个孩子是女孩”, =“2个孩子都是女孩”.
(2)“如果有1个孩子是女孩,两个孩子都是女孩”的概率就是“在事件 发生的条件下,事件 发生”的概率,记为
大 小
大 小
大 小
大 小
解:
≠P(B)
样本空间:任何性别的两个孩子的所有组合
样本空间:有1个女孩的两个孩子的所有组合
求 的一般思想:
AB
A
B
W
1、若已知事件 A 发生,则只需在 A发生的范围内考虑问题,即样本空间为A .
2、在事件A 发生的情况下事件B发生,等价于在样本空间为A的范围内,事件A和事件B同时发生.
所以事件 发生的条件下,事件 发生的概率
读作:在A发生的条件下B发生的概率.
条件概率定义:
一般地,设A,B为两个随机事件,且P(A)>0,我们称
为在事件A发生的条件下,事件B发生的条件概率.
简称条件概率.
P(AB)=P(A)P(B|A).
对任意两个事件A与B,若P(A)>0,则 P(AB)=P(A)P(B|A).
我们称上式为概率的乘法公式
例1 在5道试题中有3道代数题和2道几何题,每次从中随机抽出1道题,抽出的题不再放回. 求:
(1) 第1次抽到代数题且第2次抽到几何题的概率;
(2) 在第1次抽到代数题的条件下,第2次抽到几何题的概率.
(代1,几1)
(代1,几2)
(代2,几1)
(代2,几2)
(代3,几1)
(代3,几2)
(代1,代2)
(代1,代3)
(代2,代1)
(代2,代3)
(代3,代1)
(代3,代2)
(几1,代1)
(几1,代2)
(几1,代3)
(几1,几2)
(几2,代1)
(几2,代2)
(几2,代3)
(几2,几1)
2.概率乘法公式
1.条件概率公式:
3.求条件概率方法
方法一:条件概率定义法;
方法二:缩小样本空间法;
四、课堂小结(1分钟)
1.某地区空气质量监测资料表明,一天的空气质量为优良的概率是0.75,连续两天的空气质量为优良的概率是0.6,已知某天的空气质量为优良,则随后一天的空气质量为优良的概率是 ( )
A.0.8 B.0.75 C.0.6 D.0.45
A
五、当堂检测(12分钟)
2.一个盒子中有6个白球,4个黑球,从中不放回地每次任取1只,连取2次,则第一次取得白球的概率是________,已知第一次取得白球,那么第二次取得白球的概率是________
