沪科版数学七年级下册 10.4 平移 教案
文档属性
| 名称 | 沪科版数学七年级下册 10.4 平移 教案 |  | |
| 格式 | docx | ||
| 文件大小 | 193.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-18 14:54:02 | ||
图片预览


文档简介
相交线、平行线、平移复习课
教学目标
1.进一步熟悉对顶角、垂线、垂线段、同位角、内错角、同旁内角、平移等概念.
2.理解对顶角相等和垂线的性质,掌握平行线的判定和与性质.
3.能熟练运用本章相关知识点解题.
4.会解决简单的几何解答与证明题,会进行简单的推理,提升学生的逻辑推理能力.
5.体会数学的严谨性,体会数学的应用价值,激发学生学习数学的兴趣.
教学重点
1.会运用对顶角、垂线相关性质解决一些简单的问题.
2.会熟练运用相交线、平行线的有关性质(或判定)定理解决相关的几何题.
教学难点
综合运用本章知识点解决一些简单的几何题.
教学过程
直接说明本节课是复习课,课题是相交线、平行线、平移复习课.
进入具体复习环节.
相交线
对顶角
定义
1)请学生说出两条直线相交构成的四个角中,满足什么条件的两个角是对顶角,并请学生指出屏幕中展示的两条相交线形成的四个角中,哪些角是对顶角.
2)屏幕出示四个图,每个图中的直线交于一点,请学生判断每个图中标出的两个角是否是对顶角,并说明理由.
想一想:
n(n为不小于2的整数)条直线交于一点,形成多少对对顶角?
引导学生分别根据2条直线,3条直线,4条直线相交形成的对顶角的对数,得出n(n为不小于2的整数)条直线交于一点,形成n(n-1)对对顶角.
(2) 对顶角的性质:对顶角相等.
直线AB与CD相交于O,∠AOC:∠AOD=2:3,
求∠BOD的度数.
2.垂线
(1)引导学生回顾垂线的定义、性质以及点到直线的距离概念.
例1 已知直线AB、CD相交于点O,∠AOC=36°,EO⊥CD,垂足为O,求∠DOB,∠BOE的度数.
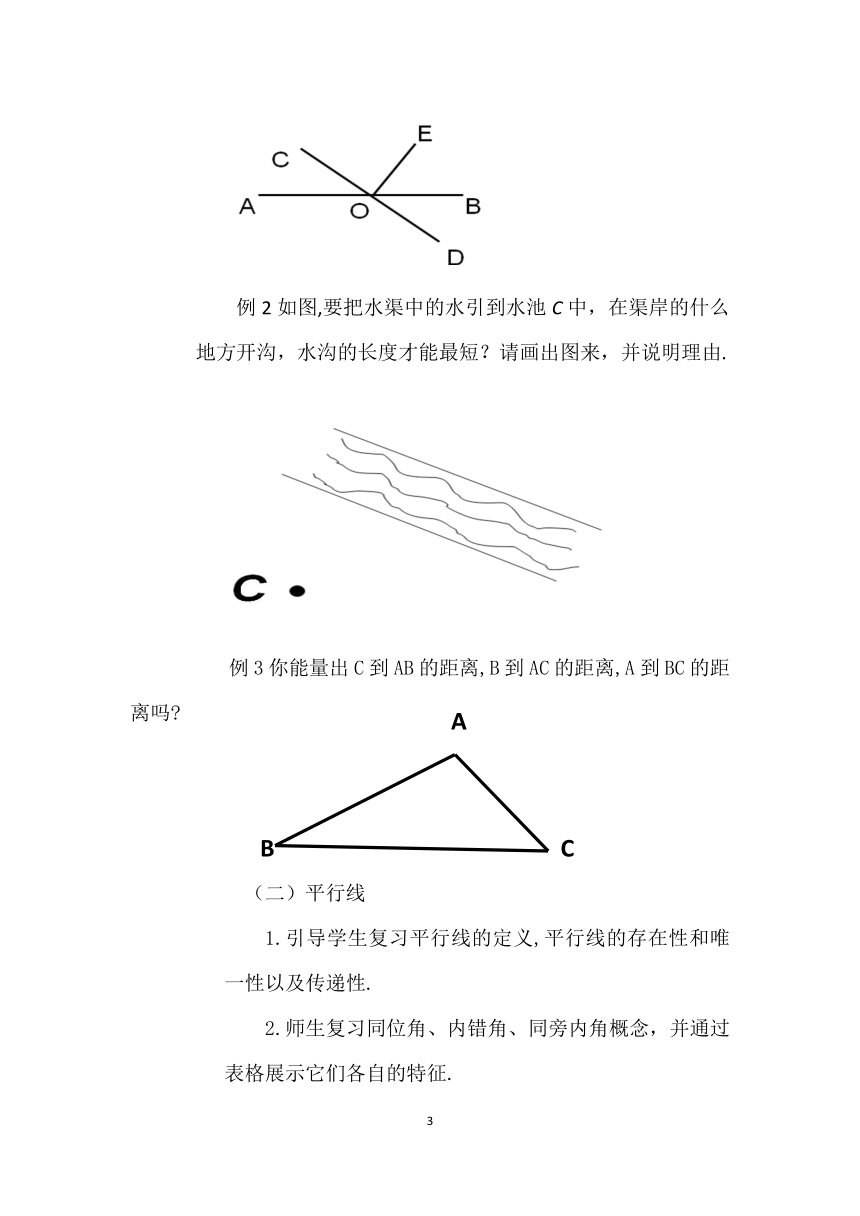
例2如图,要把水渠中的水引到水池C中,在渠岸的什么地方开沟,水沟的长度才能最短?请画出图来,并说明理由.
(
A
)例3你能量出C到AB的距离,B到AC的距离,A到BC的距离吗
B C
(二)平行线
1.引导学生复习平行线的定义,平行线的存在性和唯一性以及传递性.
2.师生复习同位角、内错角、同旁内角概念,并通过表格展示它们各自的特征.
3.引导学生回顾平行线的三种角判定方法,即同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.
练 一 练
填空
看图填空
(1)直线AB与CD被直线CE所截,与∠1成内错角的是 ,与∠1成同旁内角的是 .
(2)直线AB与CD被直线DE所截,与∠2成内错角的是 ,与∠2成同旁内角的是 .
(3)如果∠2= ∠6,那么 ∥ .
例 如图 已知:∠1+∠2=180°.求证:AB∥CD.
4.引出平行线的性质:两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.
例 如图,已知BD⊥AC,EF⊥AC,垂足分别为D、F.
求证∠1= ∠2.
(三)平移
引导学生回顾平移的定义、特点以及决定平移的因素.
练一练
(1)生活中的平移随处可见,下列属于平移现象的是()
A.升国旗
B.钟表指针的运动
C.风车的转动
D.开自来水龙头
(2)如图所示,△ABC平移到△A′B′C′的位置,则点A的对应点是____,点B的对应点是____,点C的对应点是____。线段AB的对应线段是_____,线段BC的对应线段是
______,线段AC的对应线段是_____.∠BAC的对应角是______,∠ABC的对应角是_______,∠ACB的对应角是_______.△ABC的平移方向是________,平移距离是________。
(3)指导学生完成教材P138的第1,2题.
三、课堂小结
屏幕出示本节课的主要内容.
四、布置作业
五、关于本章的一份试卷.
1
教学目标
1.进一步熟悉对顶角、垂线、垂线段、同位角、内错角、同旁内角、平移等概念.
2.理解对顶角相等和垂线的性质,掌握平行线的判定和与性质.
3.能熟练运用本章相关知识点解题.
4.会解决简单的几何解答与证明题,会进行简单的推理,提升学生的逻辑推理能力.
5.体会数学的严谨性,体会数学的应用价值,激发学生学习数学的兴趣.
教学重点
1.会运用对顶角、垂线相关性质解决一些简单的问题.
2.会熟练运用相交线、平行线的有关性质(或判定)定理解决相关的几何题.
教学难点
综合运用本章知识点解决一些简单的几何题.
教学过程
直接说明本节课是复习课,课题是相交线、平行线、平移复习课.
进入具体复习环节.
相交线
对顶角
定义
1)请学生说出两条直线相交构成的四个角中,满足什么条件的两个角是对顶角,并请学生指出屏幕中展示的两条相交线形成的四个角中,哪些角是对顶角.
2)屏幕出示四个图,每个图中的直线交于一点,请学生判断每个图中标出的两个角是否是对顶角,并说明理由.
想一想:
n(n为不小于2的整数)条直线交于一点,形成多少对对顶角?
引导学生分别根据2条直线,3条直线,4条直线相交形成的对顶角的对数,得出n(n为不小于2的整数)条直线交于一点,形成n(n-1)对对顶角.
(2) 对顶角的性质:对顶角相等.
直线AB与CD相交于O,∠AOC:∠AOD=2:3,
求∠BOD的度数.
2.垂线
(1)引导学生回顾垂线的定义、性质以及点到直线的距离概念.
例1 已知直线AB、CD相交于点O,∠AOC=36°,EO⊥CD,垂足为O,求∠DOB,∠BOE的度数.
例2如图,要把水渠中的水引到水池C中,在渠岸的什么地方开沟,水沟的长度才能最短?请画出图来,并说明理由.
(
A
)例3你能量出C到AB的距离,B到AC的距离,A到BC的距离吗
B C
(二)平行线
1.引导学生复习平行线的定义,平行线的存在性和唯一性以及传递性.
2.师生复习同位角、内错角、同旁内角概念,并通过表格展示它们各自的特征.
3.引导学生回顾平行线的三种角判定方法,即同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.
练 一 练
填空
看图填空
(1)直线AB与CD被直线CE所截,与∠1成内错角的是 ,与∠1成同旁内角的是 .
(2)直线AB与CD被直线DE所截,与∠2成内错角的是 ,与∠2成同旁内角的是 .
(3)如果∠2= ∠6,那么 ∥ .
例 如图 已知:∠1+∠2=180°.求证:AB∥CD.
4.引出平行线的性质:两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.
例 如图,已知BD⊥AC,EF⊥AC,垂足分别为D、F.
求证∠1= ∠2.
(三)平移
引导学生回顾平移的定义、特点以及决定平移的因素.
练一练
(1)生活中的平移随处可见,下列属于平移现象的是()
A.升国旗
B.钟表指针的运动
C.风车的转动
D.开自来水龙头
(2)如图所示,△ABC平移到△A′B′C′的位置,则点A的对应点是____,点B的对应点是____,点C的对应点是____。线段AB的对应线段是_____,线段BC的对应线段是
______,线段AC的对应线段是_____.∠BAC的对应角是______,∠ABC的对应角是_______,∠ACB的对应角是_______.△ABC的平移方向是________,平移距离是________。
(3)指导学生完成教材P138的第1,2题.
三、课堂小结
屏幕出示本节课的主要内容.
四、布置作业
五、关于本章的一份试卷.
1
