华师大版数学九年级上册同步课时练习 22.3 实践与探索 (word版含答案)
文档属性
| 名称 | 华师大版数学九年级上册同步课时练习 22.3 实践与探索 (word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 133.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-19 00:00:00 | ||
图片预览




文档简介
22.3 第1课时 用一元二次方程解决图形面积问题
知识点 1 一般图形的面积问题
1.用10米长的铝材制成一个矩形窗框,使矩形的面积为6平方米.若设它的一条边长为x米,则根据题意可列出关于x的方程为 ( )
A.x(5+x)=6 B.x(5-x)=6 C.x(10-x)=6 D.x(10-2x)=6
2.如图将一块正方形空地划出部分区域进行绿化,原空地一边减少了2 m,另一边减少了3 m,剩余一块面积为20 m2的矩形空地,则原正方形空地的边长是 ( )
A.7 m B.8 m C.9 m D.10 m
3.如图建造一个面积为130 m2的长方形养鸡场,养鸡场的一边靠墙,墙长为a m,另三边用竹篱笆围成,如果竹篱笆总长为33 m.
(1)求养鸡场的长与宽各为多少米;
(2)若10≤a<18,则(1)题中的解的情况如何
4.取一块长80厘米、宽60厘米的矩形铁片,在它的四个角上截去四个大小相同的正方形后,把四边折起来,做成一个无盖的长方体盒子.如果要做成底面积为1500平方厘米的长方体盒子,那么截下的正方形的边长是多少
知识点 2 边框与甬道问题
5.如图,某小区计划在一块长30 m、宽20 m的长方形ABCD土地上修建三条同样宽的甬道,使其中两条与AB平行,另一条与AD平行,其余部分种植花草.要使每一块花草的面积都为78 m2,那么甬道的宽应设计成多少米 若设甬道的宽为x m,将6块草地平移拼成一个长方形,其一边长为(30-2x)m,另一相邻边长为 m,根据长方形的面积公式可列方程 , 化成一般形式为 ,解得x1= ,x2= (不合题意,舍去).
6. 如图在一块矩形地毯的四周镶有宽度相同的花边,地毯中央的矩形图案长6米、宽3米,整个地毯的面积是40平方米.求花边的宽.
7.[2019·乐清期中] 如图,有一张边AB靠墙的长方形桌子ABCD,长120 cm,宽60 cm.有一块长方形台布EFMN的面积是桌面面积的2倍,并且如图所示铺在桌面上时,三边垂下的长度中有两边相等(AE=BF),另外一边(即CD与MN之间的距离)是AE的倍.求这块台布的长和宽.
8.扬帆中学有一块长30 m,宽20 m的矩形空地,计划在这块空地上划出四分之一的区域种花,小禹同学的设计方案如图所示,求花带的宽度.设花带的宽度为x m,则可列方程为 ( )
A.(30-x)(20-x)=×20×30 B.(30-2x)(20-x)=×20×30
C.30x+2×20x=×20×30 D.(30-2x)(20-x)=×20×30
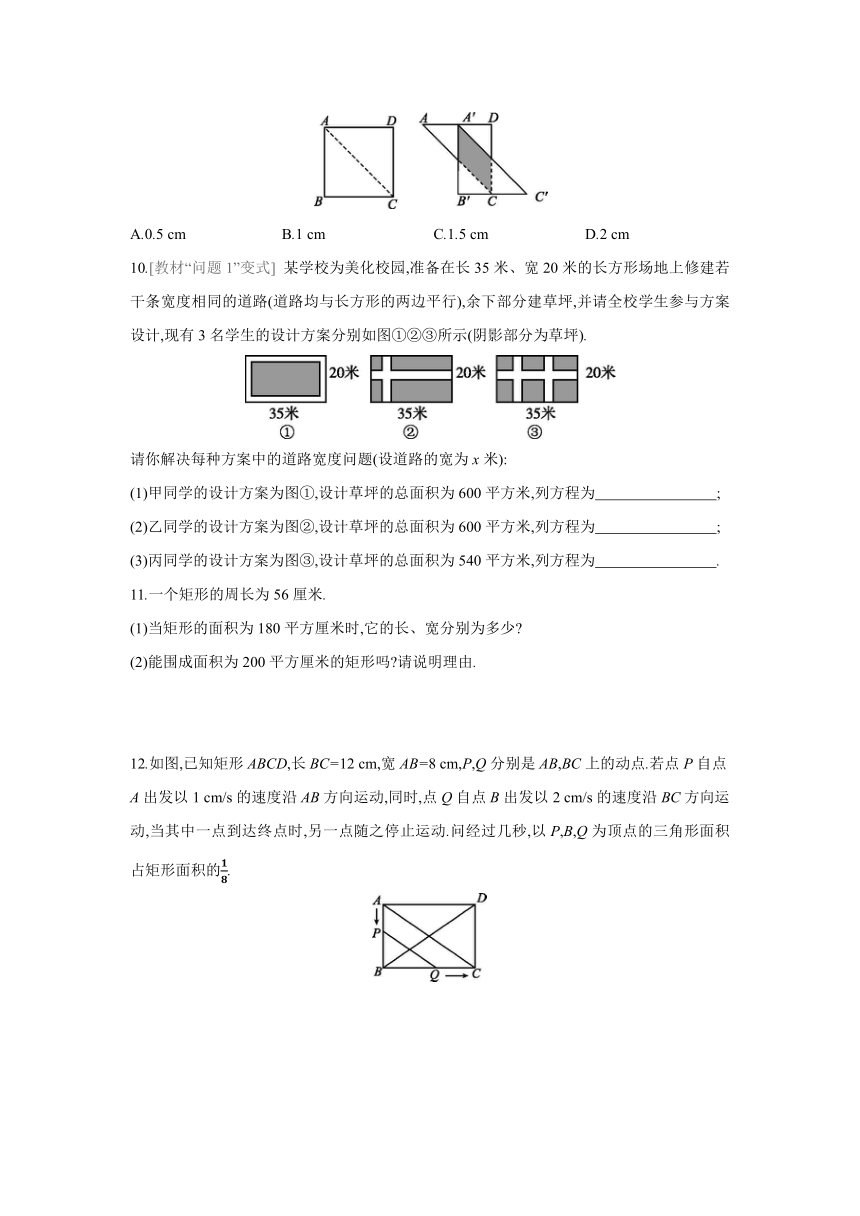
9.如图,将边长为2 cm的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A'B'C',若两个三角形重叠部分的面积为1 cm2,则它移动的距离AA'等于 ( )
A.0.5 cm B.1 cm C.1.5 cm D.2 cm
10.[教材“问题1”变式] 某学校为美化校园,准备在长35米、宽20米的长方形场地上修建若干条宽度相同的道路(道路均与长方形的两边平行),余下部分建草坪,并请全校学生参与方案设计,现有3名学生的设计方案分别如图①②③所示(阴影部分为草坪).
请你解决每种方案中的道路宽度问题(设道路的宽为x米):
(1)甲同学的设计方案为图①,设计草坪的总面积为600平方米,列方程为 ;
(2)乙同学的设计方案为图②,设计草坪的总面积为600平方米,列方程为 ;
(3)丙同学的设计方案为图③,设计草坪的总面积为540平方米,列方程为 .
11.一个矩形的周长为56厘米.
(1)当矩形的面积为180平方厘米时,它的长、宽分别为多少
(2)能围成面积为200平方厘米的矩形吗 请说明理由.
12.如图,已知矩形ABCD,长BC=12 cm,宽AB=8 cm,P,Q分别是AB,BC上的动点.若点P自点A出发以1 cm/s的速度沿AB方向运动,同时,点Q自点B出发以2 cm/s的速度沿BC方向运动,当其中一点到达终点时,另一点随之停止运动.问经过几秒,以P,B,Q为顶点的三角形面积占矩形面积的.
第2课时 用一元二次方程解决平均变化率、利润问题
知识点 1 平均变化率问题
1.[2019·赤峰] 某品牌手机三月份销售400万部,四月份、五月份销售量连续增长,五月份销售量达到900万部,求平均月增长率.设平均月增长率为x,根据题意可列方程为 ( )
A.400(1+x2)=900 B.400(1+2x)=900
C.900(1-x)2=400 D.400(1+x)2=900
2.[2019·哈尔滨] 某商品经过连续两次降价,售价由原来的每件25元降到每件16元,则平均每次降价的百分率为 ( )
A.20% B.40% C.18% D.36%
3.[教材练习第3题变式] 某地区2018年投入教育经费2500万元,2020年投入教育经费3025万元.
(1)求2018年至2020年该地区投入教育经费的年平均增长率;
(2)根据(1)所得的年平均增长率,预计2021年该地区将投入教育经费多少万元.
知识点 2 利润问题
4.某商店将进货单价为40元/个的商品按50元/个出售时,可售出500个.经市场调查发现:该商品每个每涨价1元,其销量就减少10个,商店计划赚8000元,则每个商品的售价应定为多少
解:设每个商品涨价x元,则每个商品的利润为 元,所售的个数为 个.
根据每个商品的利润×所售的个数=总利润可列方程: ,
解得x1= ,x2= ,
经检验,x的值符合题意,
所以每个商品的售价应定为 元或 元.
5.家乐商场销售某种衬衣,每件进价100元,售价160元,平均每天能售出30件.为了尽快减少库存,商场采取了降价措施.经调查发现,这种衬衣每件每降价1元,其每天的销量就增加3件.商场想要使这种衬衣的销售利润平均每天达到3600元,每件衬衣应降价 元.
6.某商店从厂家以每件18元的价格购进一批商品,该商店可自行定价,但物价部门限定每件商品加价不能超过进货价的25%.据市场调查发现,该商品的售价与销售量的关系是:若每件商品售价x元,则可卖出(320-10x)件.如果商店计划要获利400元,那么每件商品的售价应定为多少元 需要卖出这种商品多少件
7.某商店将每件进价为8元的商品按每件10元出售时,平均每天可销售200件,经市场调查发现:如果这种商品每件每涨0.5元,那么每天的销量就会减少10件.若要使平均每天的利润为640元,则需将每件商品的售价定为 ( )
A.16元 B.12元 C.16元或12元 D.14元
8.为应对金融危机,某工厂从2018年到2020年把某种产品的成本下降了19%,则平均每年下降的百分率为 .
9.“绿水青山就是金山银山”,为加快城乡绿化建设,某市2019年绿化面积约为1000万平方米,预计2021年绿化面积约为1210万平方米.假设每年绿化面积的平均增长率相同.
(1)求每年绿化面积的平均增长率;
(2)已知每平方米绿化面积的投资成本为60元,若2022年的绿化面积继续保持相同的增长率,则2022年的绿化投资成本需要多少元
10.成都放开地摊经济后,一夜之间增加近10万人就业.小王响应政府号召,摆地摊经销甲、乙两种商品.已知一件甲商品和一件乙商品进价之和为30元,每件甲商品的利润为4元,每件乙商品的售价比其进价的2倍少11元,小张在小王处购买8件甲商品和6件乙商品共用了262元.
(1)求一件甲商品和一件乙商品的进价各是多少元;
(2)小王统计发现平均每天可售出甲商品400件和乙商品300件,若将每件甲商品的售价每提高1元,则每天会少售出80件,于是小王决定将每件甲商品的价格提高a元,乙商品的售价不变,不考虑其他因素,预期每天的利润为2340元,求a的值.
11.某公司推出一款产品,经市场调查发现,该产品的日销售量y(个)与销售单价x(元/个)之间满足一次函数关系.销售单价、日销售量、日销售利润的几组对应值如下表:
销售单价x(元/个) 85 95 105 115
日销售量y(个) 175 125 75 m
日销售利润w(元) 875 1875 1875 875
注:日销售利润=日销售量×(销售单价-成本单价)
(1)求y关于x的函数表达式(不要求写出x的取值范围)及m的值;
(2)当销售单价为多少元/个时,日销售利润w为2000元
(3)公司计划开展科技创新,以降低该产品的成本,预计在今后的销售中,日销售量与销售单价仍存在(1)中的函数关系.若想实现销售单价为90元/个时,日销售利润不低于3750元的销售目标,该产品的成本单价应不超过多少元/个
答案
1.B 一边长为x米,则另外一相邻边长为(5-x)米,由题意得x(5-x)=6.故选B.
2.A 设原正方形空地的边长为x m,依题意有(x-3)(x-2)=20,
解得x1=7,x2=-2(不合题意,舍去).
即原正方形空地的边长为7 m.
3.解:(1)设养鸡场垂直于墙的一边长为x m,则平行于墙的一边长为(33-2x)m.
依题意,得(33-2x)x=130,
解得x1=6.5,x2=10,
∴33-2x1=20,33-2x2=13.
答:养鸡场的长为20 m,宽为6.5 m或长为13 m,宽为10 m.
(2)∵10≤a<18,
∴33-2x1=20不符合题意,舍去,
∴养鸡场的长为13 m,宽为10 m.
4.解:设截下的正方形的边长为x厘米.
由题意,得(80-2x)(60-2x)=1500,
解得x1 =15,x2 =55.
当x=55时,80-2x=-30,不符合题意,舍去,
所以x=15.
答:截下的正方形的边长是15厘米.
5.(20-x) (30-2x)(20-x)=78×6 x2-35x+66=0 2 33
6.解:设花边的宽为x米.
根据题意得(2x+6)(2x+3)=40,
解得x1=1,x2=-(不合题意,舍去).
答:花边的宽为1米.
7.解:设垂下的长度BF为x cm,则AE=BF=x cm,
根据题意得(120+2x)(60+x)=2×120×60,
∴x2+100x-2400=0,
解得x1=20,x2=-120(不符合题意,舍去),
∴120+2x=120+2×20=160(cm),60+x=60+×20=90(cm).
答:这块台布的长为160 cm,宽为90 cm.
8.D 设花带的宽度为x m,根据空白区域的面积=×矩形空地的面积可列方程为(30-2x)(20-x)=×20×30.故选D.
9.B 设AC交A'B'于点H.
∵∠A=45°,∠AA'H=90°,
∴△A'HA是等腰直角三角形.
设AA'=x cm,则阴影部分的一边长A'H为x cm,此边上的高A'D=(2-x)cm,
∴x(2-x)=1,
解得x1=x2=1,即AA'=1 cm.故选B.
10.(1)(35-2x)(20-2x)=600
(2)(35-x)(20-x)=600
(3)(35-2x)(20-x)=540
11. (1)设出矩形的一边长,用周长公式表示出另一相邻边长,根据面积公式列出相应方程求解即可;
(2)同样列出方程,若方程有解,则可以,否则不可以.
解:(1)设矩形的一边长为x厘米,则另一相邻边长为(28-x)厘米,依题意有
(28-x)=180,解得x1=10,x2=18.
当x=10时,28-x=18;
当x=18时,28-x=10.
故矩形的长为18厘米,宽为10厘米.
(2)不能.理由:设矩形的一边长为y厘米,则另一相邻边长为(28-y)厘米,依题意有
y(28-y)=200,
即y2-28y+200=0.
因为Δ=282-4×200=-16<0,
所以原方程无解.
故不能围成面积为200平方厘米的矩形.
12.解:设经过x秒,以P,B,Q为顶点的三角形面积占矩形面积的.
根据题意,得×2x·(8-x)=12×8×,
解得x1=2,x2=6.
∵2x≤12且x≤8,
∴x≤6,∴x1=2或x2=6均符合题意.
答:经过2秒或6秒,以P,B,Q为顶点的三角形面积占矩形面积的.
答案
1.D
2.A 设平均每次降价的百分率为x,根据题意可列方程为25(1-x)2=16,解方程得x1=,x2=(不合题意,舍去),∴平均每次降价的百分率为20%.故选A.
3.解:(1)设2018年至2020年该地区投入教育经费的年平均增长率为x.根据题意,得2019年投入教育经费2500(1+x)万元,2020年投入教育经费2500(1+x)2万元,
则2500(1+x)2=3025,
解得x1=0.1=10%,x2=-2.1(不合题意,舍去).
答:2018年至2020年该地区投入教育经费的年平均增长率为10%.
(2)3025×(1+10%)=3327.5(万元).
答:预计2021年该地区将投入教育经费3327.5万元.
4.(10+x) (500-10x) (10+x)(500-10x)=8000 30 10 80 60
5.30 设每件衬衣应降价x元,则平均每天能售出(30+3x)件,
依题意,得(160-100-x)(30+3x)=3600,
整理,得x2-50x+600=0,
解得x1=20,x2=30.
∵为了尽快减少库存,∴x=30.
故每件衬衣应降价30元.
6.解:根据每件售价x元,物价部门限定每件商品加价不能超过进货价的25%,
得x≤18×(1+25%)=22.5(元).
根据等量关系:(每件商品的售价-每件商品的进价)×售出件数=利润可得方程
(x-18)(320-10x)=400,
解得x1=22,x2=28(不合题意,舍去),
卖出这种商品的件数是320-10x=320-10×22=100(件).
答:每件商品的售价应定为22元,需要卖出这种商品100件.
7.C 设每件商品的售价为x元,根据题意列方程得
(x-8)(200-×10)=640,
整理得x2-28x+192=0,
解得x1=12,x2=16.
故选C.
8.10% 设平均每年下降的百分率为x,原产品的成本为a.
由题意,得a(1-x)2=(1-19%)a,
解得x1=0.1=10%,x2=1.9(不合题意,舍去).
所以平均每年下降的百分率为10%.
故答案为10%.
9.解:(1)设每年绿化面积的平均增长率为x.
可列方程:1000(1+x)2=1210.
解方程,得x1=0.1=10%,x2=-2.1(不合题意,舍去).
所以每年绿化面积的平均增长率为10%.
(2)1210×(1+10%)=1331(万平方米),
13310000×60=798600000(元).
答:2022年的绿化投资成本需要798600000元.
10.解:(1)设一件甲商品的进价是x元,一件乙商品的进价是y元,则一件甲商品的售价为(x+4)元,一件乙商品的售价为(2y-11)元.
依题意,得
解得
答:一件甲商品的进价是16元,一件乙商品的进价是14元.
(2)依题意,得(4+a)(400-80a)+(2×14-11-14)×300=2340,
整理,得a2-a-2=0,
解得a1=2,a2=-1(不合题意,舍去).
答:a的值为2.
11.解:(1)设y关于x的函数表达式为y=kx+b(k≠0).
将(85,175),(95,125)代入y=kx+b,得
解得
∴y关于x的函数表达式为y=-5x+600.
当x=115时,y=-5×115+600=25,
即m=25.
(2)该产品的成本单价为85-875÷175=80(元/个).
当w=2000时,(x-80)(-5x+600)=2000,
整理,得x2-200x+10000=0,
解得x1=x2=100.
故当销售单价为100元/个时,日销售利润w为2000元.
(3)设该产品的成本单价为a元/个.
依题意,得(90-a)(-5×90+600)≥3750,
解得a≤65.
答:该产品的成本单价应不超过65元/个.
知识点 1 一般图形的面积问题
1.用10米长的铝材制成一个矩形窗框,使矩形的面积为6平方米.若设它的一条边长为x米,则根据题意可列出关于x的方程为 ( )
A.x(5+x)=6 B.x(5-x)=6 C.x(10-x)=6 D.x(10-2x)=6
2.如图将一块正方形空地划出部分区域进行绿化,原空地一边减少了2 m,另一边减少了3 m,剩余一块面积为20 m2的矩形空地,则原正方形空地的边长是 ( )
A.7 m B.8 m C.9 m D.10 m
3.如图建造一个面积为130 m2的长方形养鸡场,养鸡场的一边靠墙,墙长为a m,另三边用竹篱笆围成,如果竹篱笆总长为33 m.
(1)求养鸡场的长与宽各为多少米;
(2)若10≤a<18,则(1)题中的解的情况如何
4.取一块长80厘米、宽60厘米的矩形铁片,在它的四个角上截去四个大小相同的正方形后,把四边折起来,做成一个无盖的长方体盒子.如果要做成底面积为1500平方厘米的长方体盒子,那么截下的正方形的边长是多少
知识点 2 边框与甬道问题
5.如图,某小区计划在一块长30 m、宽20 m的长方形ABCD土地上修建三条同样宽的甬道,使其中两条与AB平行,另一条与AD平行,其余部分种植花草.要使每一块花草的面积都为78 m2,那么甬道的宽应设计成多少米 若设甬道的宽为x m,将6块草地平移拼成一个长方形,其一边长为(30-2x)m,另一相邻边长为 m,根据长方形的面积公式可列方程 , 化成一般形式为 ,解得x1= ,x2= (不合题意,舍去).
6. 如图在一块矩形地毯的四周镶有宽度相同的花边,地毯中央的矩形图案长6米、宽3米,整个地毯的面积是40平方米.求花边的宽.
7.[2019·乐清期中] 如图,有一张边AB靠墙的长方形桌子ABCD,长120 cm,宽60 cm.有一块长方形台布EFMN的面积是桌面面积的2倍,并且如图所示铺在桌面上时,三边垂下的长度中有两边相等(AE=BF),另外一边(即CD与MN之间的距离)是AE的倍.求这块台布的长和宽.
8.扬帆中学有一块长30 m,宽20 m的矩形空地,计划在这块空地上划出四分之一的区域种花,小禹同学的设计方案如图所示,求花带的宽度.设花带的宽度为x m,则可列方程为 ( )
A.(30-x)(20-x)=×20×30 B.(30-2x)(20-x)=×20×30
C.30x+2×20x=×20×30 D.(30-2x)(20-x)=×20×30
9.如图,将边长为2 cm的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A'B'C',若两个三角形重叠部分的面积为1 cm2,则它移动的距离AA'等于 ( )
A.0.5 cm B.1 cm C.1.5 cm D.2 cm
10.[教材“问题1”变式] 某学校为美化校园,准备在长35米、宽20米的长方形场地上修建若干条宽度相同的道路(道路均与长方形的两边平行),余下部分建草坪,并请全校学生参与方案设计,现有3名学生的设计方案分别如图①②③所示(阴影部分为草坪).
请你解决每种方案中的道路宽度问题(设道路的宽为x米):
(1)甲同学的设计方案为图①,设计草坪的总面积为600平方米,列方程为 ;
(2)乙同学的设计方案为图②,设计草坪的总面积为600平方米,列方程为 ;
(3)丙同学的设计方案为图③,设计草坪的总面积为540平方米,列方程为 .
11.一个矩形的周长为56厘米.
(1)当矩形的面积为180平方厘米时,它的长、宽分别为多少
(2)能围成面积为200平方厘米的矩形吗 请说明理由.
12.如图,已知矩形ABCD,长BC=12 cm,宽AB=8 cm,P,Q分别是AB,BC上的动点.若点P自点A出发以1 cm/s的速度沿AB方向运动,同时,点Q自点B出发以2 cm/s的速度沿BC方向运动,当其中一点到达终点时,另一点随之停止运动.问经过几秒,以P,B,Q为顶点的三角形面积占矩形面积的.
第2课时 用一元二次方程解决平均变化率、利润问题
知识点 1 平均变化率问题
1.[2019·赤峰] 某品牌手机三月份销售400万部,四月份、五月份销售量连续增长,五月份销售量达到900万部,求平均月增长率.设平均月增长率为x,根据题意可列方程为 ( )
A.400(1+x2)=900 B.400(1+2x)=900
C.900(1-x)2=400 D.400(1+x)2=900
2.[2019·哈尔滨] 某商品经过连续两次降价,售价由原来的每件25元降到每件16元,则平均每次降价的百分率为 ( )
A.20% B.40% C.18% D.36%
3.[教材练习第3题变式] 某地区2018年投入教育经费2500万元,2020年投入教育经费3025万元.
(1)求2018年至2020年该地区投入教育经费的年平均增长率;
(2)根据(1)所得的年平均增长率,预计2021年该地区将投入教育经费多少万元.
知识点 2 利润问题
4.某商店将进货单价为40元/个的商品按50元/个出售时,可售出500个.经市场调查发现:该商品每个每涨价1元,其销量就减少10个,商店计划赚8000元,则每个商品的售价应定为多少
解:设每个商品涨价x元,则每个商品的利润为 元,所售的个数为 个.
根据每个商品的利润×所售的个数=总利润可列方程: ,
解得x1= ,x2= ,
经检验,x的值符合题意,
所以每个商品的售价应定为 元或 元.
5.家乐商场销售某种衬衣,每件进价100元,售价160元,平均每天能售出30件.为了尽快减少库存,商场采取了降价措施.经调查发现,这种衬衣每件每降价1元,其每天的销量就增加3件.商场想要使这种衬衣的销售利润平均每天达到3600元,每件衬衣应降价 元.
6.某商店从厂家以每件18元的价格购进一批商品,该商店可自行定价,但物价部门限定每件商品加价不能超过进货价的25%.据市场调查发现,该商品的售价与销售量的关系是:若每件商品售价x元,则可卖出(320-10x)件.如果商店计划要获利400元,那么每件商品的售价应定为多少元 需要卖出这种商品多少件
7.某商店将每件进价为8元的商品按每件10元出售时,平均每天可销售200件,经市场调查发现:如果这种商品每件每涨0.5元,那么每天的销量就会减少10件.若要使平均每天的利润为640元,则需将每件商品的售价定为 ( )
A.16元 B.12元 C.16元或12元 D.14元
8.为应对金融危机,某工厂从2018年到2020年把某种产品的成本下降了19%,则平均每年下降的百分率为 .
9.“绿水青山就是金山银山”,为加快城乡绿化建设,某市2019年绿化面积约为1000万平方米,预计2021年绿化面积约为1210万平方米.假设每年绿化面积的平均增长率相同.
(1)求每年绿化面积的平均增长率;
(2)已知每平方米绿化面积的投资成本为60元,若2022年的绿化面积继续保持相同的增长率,则2022年的绿化投资成本需要多少元
10.成都放开地摊经济后,一夜之间增加近10万人就业.小王响应政府号召,摆地摊经销甲、乙两种商品.已知一件甲商品和一件乙商品进价之和为30元,每件甲商品的利润为4元,每件乙商品的售价比其进价的2倍少11元,小张在小王处购买8件甲商品和6件乙商品共用了262元.
(1)求一件甲商品和一件乙商品的进价各是多少元;
(2)小王统计发现平均每天可售出甲商品400件和乙商品300件,若将每件甲商品的售价每提高1元,则每天会少售出80件,于是小王决定将每件甲商品的价格提高a元,乙商品的售价不变,不考虑其他因素,预期每天的利润为2340元,求a的值.
11.某公司推出一款产品,经市场调查发现,该产品的日销售量y(个)与销售单价x(元/个)之间满足一次函数关系.销售单价、日销售量、日销售利润的几组对应值如下表:
销售单价x(元/个) 85 95 105 115
日销售量y(个) 175 125 75 m
日销售利润w(元) 875 1875 1875 875
注:日销售利润=日销售量×(销售单价-成本单价)
(1)求y关于x的函数表达式(不要求写出x的取值范围)及m的值;
(2)当销售单价为多少元/个时,日销售利润w为2000元
(3)公司计划开展科技创新,以降低该产品的成本,预计在今后的销售中,日销售量与销售单价仍存在(1)中的函数关系.若想实现销售单价为90元/个时,日销售利润不低于3750元的销售目标,该产品的成本单价应不超过多少元/个
答案
1.B 一边长为x米,则另外一相邻边长为(5-x)米,由题意得x(5-x)=6.故选B.
2.A 设原正方形空地的边长为x m,依题意有(x-3)(x-2)=20,
解得x1=7,x2=-2(不合题意,舍去).
即原正方形空地的边长为7 m.
3.解:(1)设养鸡场垂直于墙的一边长为x m,则平行于墙的一边长为(33-2x)m.
依题意,得(33-2x)x=130,
解得x1=6.5,x2=10,
∴33-2x1=20,33-2x2=13.
答:养鸡场的长为20 m,宽为6.5 m或长为13 m,宽为10 m.
(2)∵10≤a<18,
∴33-2x1=20不符合题意,舍去,
∴养鸡场的长为13 m,宽为10 m.
4.解:设截下的正方形的边长为x厘米.
由题意,得(80-2x)(60-2x)=1500,
解得x1 =15,x2 =55.
当x=55时,80-2x=-30,不符合题意,舍去,
所以x=15.
答:截下的正方形的边长是15厘米.
5.(20-x) (30-2x)(20-x)=78×6 x2-35x+66=0 2 33
6.解:设花边的宽为x米.
根据题意得(2x+6)(2x+3)=40,
解得x1=1,x2=-(不合题意,舍去).
答:花边的宽为1米.
7.解:设垂下的长度BF为x cm,则AE=BF=x cm,
根据题意得(120+2x)(60+x)=2×120×60,
∴x2+100x-2400=0,
解得x1=20,x2=-120(不符合题意,舍去),
∴120+2x=120+2×20=160(cm),60+x=60+×20=90(cm).
答:这块台布的长为160 cm,宽为90 cm.
8.D 设花带的宽度为x m,根据空白区域的面积=×矩形空地的面积可列方程为(30-2x)(20-x)=×20×30.故选D.
9.B 设AC交A'B'于点H.
∵∠A=45°,∠AA'H=90°,
∴△A'HA是等腰直角三角形.
设AA'=x cm,则阴影部分的一边长A'H为x cm,此边上的高A'D=(2-x)cm,
∴x(2-x)=1,
解得x1=x2=1,即AA'=1 cm.故选B.
10.(1)(35-2x)(20-2x)=600
(2)(35-x)(20-x)=600
(3)(35-2x)(20-x)=540
11. (1)设出矩形的一边长,用周长公式表示出另一相邻边长,根据面积公式列出相应方程求解即可;
(2)同样列出方程,若方程有解,则可以,否则不可以.
解:(1)设矩形的一边长为x厘米,则另一相邻边长为(28-x)厘米,依题意有
(28-x)=180,解得x1=10,x2=18.
当x=10时,28-x=18;
当x=18时,28-x=10.
故矩形的长为18厘米,宽为10厘米.
(2)不能.理由:设矩形的一边长为y厘米,则另一相邻边长为(28-y)厘米,依题意有
y(28-y)=200,
即y2-28y+200=0.
因为Δ=282-4×200=-16<0,
所以原方程无解.
故不能围成面积为200平方厘米的矩形.
12.解:设经过x秒,以P,B,Q为顶点的三角形面积占矩形面积的.
根据题意,得×2x·(8-x)=12×8×,
解得x1=2,x2=6.
∵2x≤12且x≤8,
∴x≤6,∴x1=2或x2=6均符合题意.
答:经过2秒或6秒,以P,B,Q为顶点的三角形面积占矩形面积的.
答案
1.D
2.A 设平均每次降价的百分率为x,根据题意可列方程为25(1-x)2=16,解方程得x1=,x2=(不合题意,舍去),∴平均每次降价的百分率为20%.故选A.
3.解:(1)设2018年至2020年该地区投入教育经费的年平均增长率为x.根据题意,得2019年投入教育经费2500(1+x)万元,2020年投入教育经费2500(1+x)2万元,
则2500(1+x)2=3025,
解得x1=0.1=10%,x2=-2.1(不合题意,舍去).
答:2018年至2020年该地区投入教育经费的年平均增长率为10%.
(2)3025×(1+10%)=3327.5(万元).
答:预计2021年该地区将投入教育经费3327.5万元.
4.(10+x) (500-10x) (10+x)(500-10x)=8000 30 10 80 60
5.30 设每件衬衣应降价x元,则平均每天能售出(30+3x)件,
依题意,得(160-100-x)(30+3x)=3600,
整理,得x2-50x+600=0,
解得x1=20,x2=30.
∵为了尽快减少库存,∴x=30.
故每件衬衣应降价30元.
6.解:根据每件售价x元,物价部门限定每件商品加价不能超过进货价的25%,
得x≤18×(1+25%)=22.5(元).
根据等量关系:(每件商品的售价-每件商品的进价)×售出件数=利润可得方程
(x-18)(320-10x)=400,
解得x1=22,x2=28(不合题意,舍去),
卖出这种商品的件数是320-10x=320-10×22=100(件).
答:每件商品的售价应定为22元,需要卖出这种商品100件.
7.C 设每件商品的售价为x元,根据题意列方程得
(x-8)(200-×10)=640,
整理得x2-28x+192=0,
解得x1=12,x2=16.
故选C.
8.10% 设平均每年下降的百分率为x,原产品的成本为a.
由题意,得a(1-x)2=(1-19%)a,
解得x1=0.1=10%,x2=1.9(不合题意,舍去).
所以平均每年下降的百分率为10%.
故答案为10%.
9.解:(1)设每年绿化面积的平均增长率为x.
可列方程:1000(1+x)2=1210.
解方程,得x1=0.1=10%,x2=-2.1(不合题意,舍去).
所以每年绿化面积的平均增长率为10%.
(2)1210×(1+10%)=1331(万平方米),
13310000×60=798600000(元).
答:2022年的绿化投资成本需要798600000元.
10.解:(1)设一件甲商品的进价是x元,一件乙商品的进价是y元,则一件甲商品的售价为(x+4)元,一件乙商品的售价为(2y-11)元.
依题意,得
解得
答:一件甲商品的进价是16元,一件乙商品的进价是14元.
(2)依题意,得(4+a)(400-80a)+(2×14-11-14)×300=2340,
整理,得a2-a-2=0,
解得a1=2,a2=-1(不合题意,舍去).
答:a的值为2.
11.解:(1)设y关于x的函数表达式为y=kx+b(k≠0).
将(85,175),(95,125)代入y=kx+b,得
解得
∴y关于x的函数表达式为y=-5x+600.
当x=115时,y=-5×115+600=25,
即m=25.
(2)该产品的成本单价为85-875÷175=80(元/个).
当w=2000时,(x-80)(-5x+600)=2000,
整理,得x2-200x+10000=0,
解得x1=x2=100.
故当销售单价为100元/个时,日销售利润w为2000元.
(3)设该产品的成本单价为a元/个.
依题意,得(90-a)(-5×90+600)≥3750,
解得a≤65.
答:该产品的成本单价应不超过65元/个.
