华师大版数学九年级上册同步课时练习 23.3.1相似三角形 (word版含答案)
文档属性
| 名称 | 华师大版数学九年级上册同步课时练习 23.3.1相似三角形 (word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 136.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-19 06:48:23 | ||
图片预览



文档简介
23.3.1 相似三角形
知识点 1 相似三角形的有关概念
1.已知△ABC∽△A'B'C',AB=6 cm,其对应边A'B'=4 cm,则△ABC与△A'B'C'的相似比为 .
2.已知△ABC∽△A'B'C',且△ABC与△A'B'C'的相似比是,则△A'B'C'与△ABC的相似比是( )
A. B. C. D.
3.如图,Rt△ADC∽Rt△DBC,AC=3,BC=4,试求△ADC与△DBC的相似比.
知识点 2 相似三角形对应边、对应角的识别
4.如图,△AED∽△ABC,且∠1=∠B=50°,∠C=70°,则∠2= °,=.
5.在△ABC中,∠A=45°,∠B=35°,则与△ABC相似的三角形三个内角的度数分别为 ( )
A.35°,45°,45° B.45°,105°,35°
C.45°,35°,110° D.45°,35°,100°
6.已知△ABC与△DEF相似,且∠A=50°,∠B=70°,∠C=60°,∠D=60°,∠E=70°,则 ( )
A.∠F=50°,AB与DE是对应边
B.∠F=50°,AB与EF是对应边
C.∠F=50°,AB与DF是对应边
D.AB与DE,AC与DF,BC与EF是三组对应边
7.如图所示,根据下列情况写出各组相似三角形的对应边的比例式.
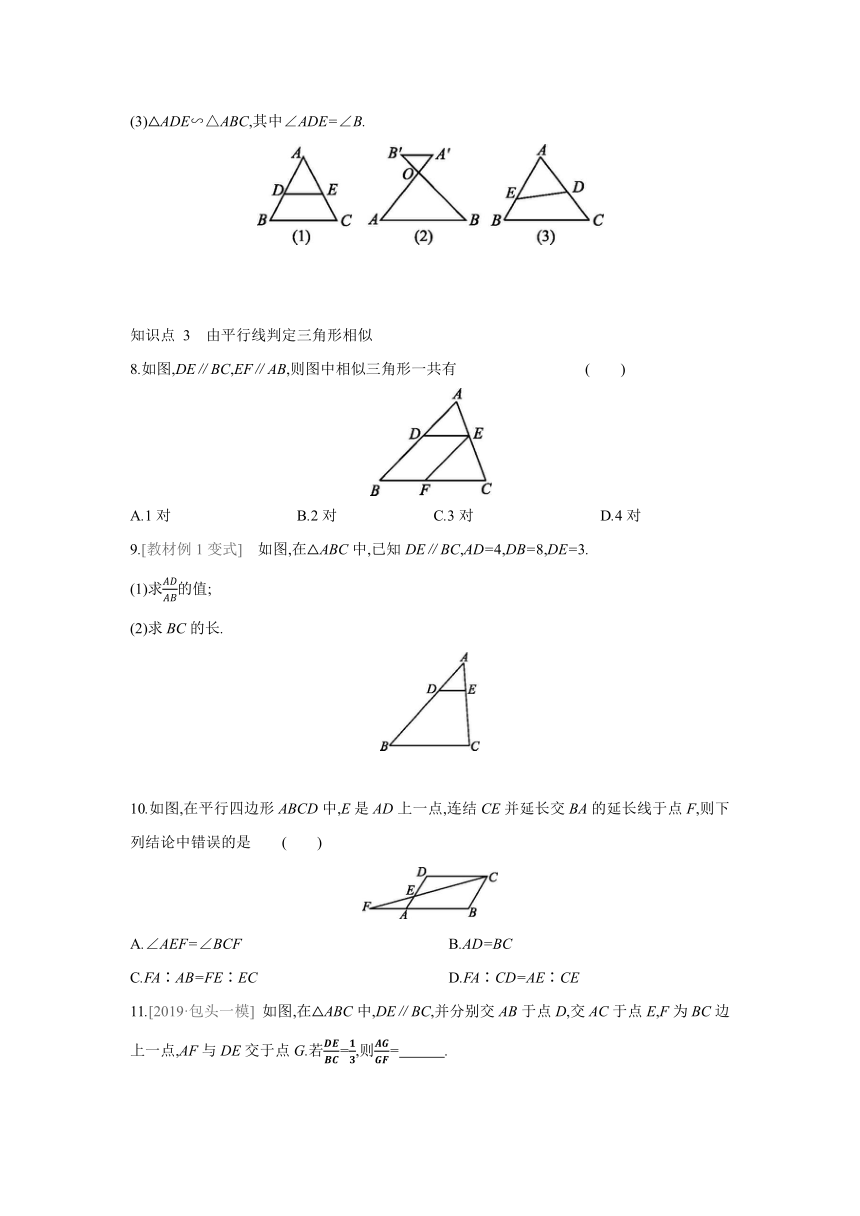
(1)△ABC∽△ADE,其中DE∥BC;
(2)△OAB∽△OA'B',其中A'B'∥AB;
(3)△ADE∽△ABC,其中∠ADE=∠B.
知识点 3 由平行线判定三角形相似
8.如图,DE∥BC,EF∥AB,则图中相似三角形一共有 ( )
A.1对 B.2对 C.3对 D.4对
9.[教材例1变式] 如图,在△ABC中,已知DE∥BC,AD=4,DB=8,DE=3.
(1)求的值;
(2)求BC的长.
10.如图,在平行四边形ABCD中,E是AD上一点,连结CE并延长交BA的延长线于点F,则下列结论中错误的是 ( )
A.∠AEF=∠BCF B.AD=BC
C.FA∶AB=FE∶EC D.FA∶CD=AE∶CE
11.[2019·包头一模] 如图,在△ABC中,DE∥BC,并分别交AB于点D,交AC于点E,F为BC边上一点,AF与DE交于点G.若=,则= .
12.已知△ABC与△A1B1C1的相似比为2∶3,△A1B1C1与△A2B2C2的相似比为3∶5,那么△ABC与△A2B2C2的相似比为 .
13.已知△ABC的三边长分别为,,2,△A'B'C'的两边长分别为1和.若△ABC∽△A'B'C',则△A'B'C'的第三边长为 .
14. 如图所示,在 ABCD中,E是BC上一点,BE∶EC=2∶3,AE交BD于点F,则BF∶DF= .
15.如图,AB∥GH∥DC,点H在BC上,AC与BD交于点G,AB=2,DC=3,求GH的长.
16.先阅读下列材料,然后解答问题.
材料:从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.例如:如图①,AD把△ABC分成△ABD与△ADC,如果△ABD是等腰三角形,且△ADC∽△BAC,那么AD就是△ABC的完美分割线.
解答下列问题:
(1)如图②,在△ABC中,∠B=40°,AD是△ABC的完美分割线,且△ABD是以AD为底边的等腰三角形,则∠CAD= 度.
(2)在△ABC中,∠B=42°,AD是△ABC的完美分割线,且△ABD是等腰三角形,求∠BAC的度数.
答案
1. 2.B
3.解:∵Rt△ADC∽Rt△DBC,
∴=,即=,
∴DC2=12,则DC=2,
∴△ADC与△DBC的相似比为=.
4.70 AC ED ∠2=∠C=70°,=.
5.D 利用相似三角形的对应角相等可以获解.
6.B
7.解:(1)==.
(2)==.
(3)==.
8.C ∵DE∥BC,
∴△ADE∽△ABC.
∵EF∥AB,∴△CEF∽△CAB,
∴△ADE∽△EFC,共3对.
故选C.
9. (1)由已知条件求得AB的长,再求即可;
(2)已知DE∥BC,可得△ADE∽△ABC,可得出=.
解:(1)∵AD=4,DB=8,
∴AB=AD+DB=4+8=12,
∴==.
(2)∵DE∥BC,
∴△ADE∽△ABC,
∴=.
∵DE=3,
∴=,
∴BC=9.
10.D ∵四边形ABCD为平行四边形,
∴AD∥BC,AD=BC,
∴∠AEF=∠BCF,
∴A,B选项的结论正确,不符合题意;
∵AE∥BC,
∴FA∶AB=FE∶EC,
∴C选项的结论正确,不符合题意;
∵四边形ABCD为平行四边形,
∴AB∥CD,
∴△AEF∽△DEC,
∴FA∶CD=AE∶DE,
∴D选项的结论错误,符合题意.
故选D.
11. ∵DE∥BC,∴△ADE∽△ABC,
∴==.
同理:△ADG∽△ABF,∴==.
∵AF=AG+GF,
∴===.
故答案为.
12.2∶5 ∵△ABC与△A1B1C1的相似比为2∶3,△A1B1C1与△A2B2C2的相似比为3∶5,∴AB∶A1B1=2∶3,A1B1∶A2B2=3∶5.
设AB=2x,则A1B1=3x,A2B2=5x,
∴AB∶A2B2=2∶5,
∴△ABC与△A2B2C2的相似比为2∶5.
13. ∵=,
∴两三角形的相似比为,
∴△A'B'C'的第三边长为=.
14.2∶5 ∵四边形ABCD是平行四边形,∴DA∥BC,DA=BC,∴△BEF∽△DAF,
∴BF∶DF=BE∶DA.
∵BE∶EC=2∶3,
∴BE∶BC=2∶5.
又∵BC=DA,
∴BE∶DA=2∶5,
∴BF∶DF=2∶5.
15.解:∵AB∥GH∥DC,
∴△CGH∽△CAB,△BGH∽△BDC,
∴=,=,
∴+=+=1.
∵AB=2,DC=3,
∴+=1,∴GH=.
16.解:(1)40 ∵AD是△ABC的完美分割线,
∴△ADC∽△BAC,
∴∠CAD=∠B=40°.
(2)△ABD是等腰三角形,分情况讨论:
若BD=AD,则∠ABD=∠BAD=42°.
∵AD是△ABC的完美分割线,
∴△ADC∽△BAC,
∴∠CAD=∠B=42°,
∴∠BAC=∠BAD+∠CAD=84°;
若AB=BD,
则∠BAD=69°=∠BDA.
∵AD是△ABC的完美分割线,
∴△ADC∽△BAC,
∴∠CAD=∠B=42°,
∴∠BAC=∠BAD+∠CAD=42°+69°=111°;
若AB=AD,
则∠B=∠ADB=42°.
∵AD是△ABC的完美分割线,
∴△ADC∽△BAC,
∴∠CAD=∠B=42°.
∵∠ADB=∠CAD+∠C=42°+∠C≠42°,
∴不存在AB=AD.
综上所述,∠BAC的度数为84°或111°.
知识点 1 相似三角形的有关概念
1.已知△ABC∽△A'B'C',AB=6 cm,其对应边A'B'=4 cm,则△ABC与△A'B'C'的相似比为 .
2.已知△ABC∽△A'B'C',且△ABC与△A'B'C'的相似比是,则△A'B'C'与△ABC的相似比是( )
A. B. C. D.
3.如图,Rt△ADC∽Rt△DBC,AC=3,BC=4,试求△ADC与△DBC的相似比.
知识点 2 相似三角形对应边、对应角的识别
4.如图,△AED∽△ABC,且∠1=∠B=50°,∠C=70°,则∠2= °,=.
5.在△ABC中,∠A=45°,∠B=35°,则与△ABC相似的三角形三个内角的度数分别为 ( )
A.35°,45°,45° B.45°,105°,35°
C.45°,35°,110° D.45°,35°,100°
6.已知△ABC与△DEF相似,且∠A=50°,∠B=70°,∠C=60°,∠D=60°,∠E=70°,则 ( )
A.∠F=50°,AB与DE是对应边
B.∠F=50°,AB与EF是对应边
C.∠F=50°,AB与DF是对应边
D.AB与DE,AC与DF,BC与EF是三组对应边
7.如图所示,根据下列情况写出各组相似三角形的对应边的比例式.
(1)△ABC∽△ADE,其中DE∥BC;
(2)△OAB∽△OA'B',其中A'B'∥AB;
(3)△ADE∽△ABC,其中∠ADE=∠B.
知识点 3 由平行线判定三角形相似
8.如图,DE∥BC,EF∥AB,则图中相似三角形一共有 ( )
A.1对 B.2对 C.3对 D.4对
9.[教材例1变式] 如图,在△ABC中,已知DE∥BC,AD=4,DB=8,DE=3.
(1)求的值;
(2)求BC的长.
10.如图,在平行四边形ABCD中,E是AD上一点,连结CE并延长交BA的延长线于点F,则下列结论中错误的是 ( )
A.∠AEF=∠BCF B.AD=BC
C.FA∶AB=FE∶EC D.FA∶CD=AE∶CE
11.[2019·包头一模] 如图,在△ABC中,DE∥BC,并分别交AB于点D,交AC于点E,F为BC边上一点,AF与DE交于点G.若=,则= .
12.已知△ABC与△A1B1C1的相似比为2∶3,△A1B1C1与△A2B2C2的相似比为3∶5,那么△ABC与△A2B2C2的相似比为 .
13.已知△ABC的三边长分别为,,2,△A'B'C'的两边长分别为1和.若△ABC∽△A'B'C',则△A'B'C'的第三边长为 .
14. 如图所示,在 ABCD中,E是BC上一点,BE∶EC=2∶3,AE交BD于点F,则BF∶DF= .
15.如图,AB∥GH∥DC,点H在BC上,AC与BD交于点G,AB=2,DC=3,求GH的长.
16.先阅读下列材料,然后解答问题.
材料:从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.例如:如图①,AD把△ABC分成△ABD与△ADC,如果△ABD是等腰三角形,且△ADC∽△BAC,那么AD就是△ABC的完美分割线.
解答下列问题:
(1)如图②,在△ABC中,∠B=40°,AD是△ABC的完美分割线,且△ABD是以AD为底边的等腰三角形,则∠CAD= 度.
(2)在△ABC中,∠B=42°,AD是△ABC的完美分割线,且△ABD是等腰三角形,求∠BAC的度数.
答案
1. 2.B
3.解:∵Rt△ADC∽Rt△DBC,
∴=,即=,
∴DC2=12,则DC=2,
∴△ADC与△DBC的相似比为=.
4.70 AC ED ∠2=∠C=70°,=.
5.D 利用相似三角形的对应角相等可以获解.
6.B
7.解:(1)==.
(2)==.
(3)==.
8.C ∵DE∥BC,
∴△ADE∽△ABC.
∵EF∥AB,∴△CEF∽△CAB,
∴△ADE∽△EFC,共3对.
故选C.
9. (1)由已知条件求得AB的长,再求即可;
(2)已知DE∥BC,可得△ADE∽△ABC,可得出=.
解:(1)∵AD=4,DB=8,
∴AB=AD+DB=4+8=12,
∴==.
(2)∵DE∥BC,
∴△ADE∽△ABC,
∴=.
∵DE=3,
∴=,
∴BC=9.
10.D ∵四边形ABCD为平行四边形,
∴AD∥BC,AD=BC,
∴∠AEF=∠BCF,
∴A,B选项的结论正确,不符合题意;
∵AE∥BC,
∴FA∶AB=FE∶EC,
∴C选项的结论正确,不符合题意;
∵四边形ABCD为平行四边形,
∴AB∥CD,
∴△AEF∽△DEC,
∴FA∶CD=AE∶DE,
∴D选项的结论错误,符合题意.
故选D.
11. ∵DE∥BC,∴△ADE∽△ABC,
∴==.
同理:△ADG∽△ABF,∴==.
∵AF=AG+GF,
∴===.
故答案为.
12.2∶5 ∵△ABC与△A1B1C1的相似比为2∶3,△A1B1C1与△A2B2C2的相似比为3∶5,∴AB∶A1B1=2∶3,A1B1∶A2B2=3∶5.
设AB=2x,则A1B1=3x,A2B2=5x,
∴AB∶A2B2=2∶5,
∴△ABC与△A2B2C2的相似比为2∶5.
13. ∵=,
∴两三角形的相似比为,
∴△A'B'C'的第三边长为=.
14.2∶5 ∵四边形ABCD是平行四边形,∴DA∥BC,DA=BC,∴△BEF∽△DAF,
∴BF∶DF=BE∶DA.
∵BE∶EC=2∶3,
∴BE∶BC=2∶5.
又∵BC=DA,
∴BE∶DA=2∶5,
∴BF∶DF=2∶5.
15.解:∵AB∥GH∥DC,
∴△CGH∽△CAB,△BGH∽△BDC,
∴=,=,
∴+=+=1.
∵AB=2,DC=3,
∴+=1,∴GH=.
16.解:(1)40 ∵AD是△ABC的完美分割线,
∴△ADC∽△BAC,
∴∠CAD=∠B=40°.
(2)△ABD是等腰三角形,分情况讨论:
若BD=AD,则∠ABD=∠BAD=42°.
∵AD是△ABC的完美分割线,
∴△ADC∽△BAC,
∴∠CAD=∠B=42°,
∴∠BAC=∠BAD+∠CAD=84°;
若AB=BD,
则∠BAD=69°=∠BDA.
∵AD是△ABC的完美分割线,
∴△ADC∽△BAC,
∴∠CAD=∠B=42°,
∴∠BAC=∠BAD+∠CAD=42°+69°=111°;
若AB=AD,
则∠B=∠ADB=42°.
∵AD是△ABC的完美分割线,
∴△ADC∽△BAC,
∴∠CAD=∠B=42°.
∵∠ADB=∠CAD+∠C=42°+∠C≠42°,
∴不存在AB=AD.
综上所述,∠BAC的度数为84°或111°.
