华师大版数学九年级上册同步课时练习:23.3.3 相似三角形的性质(word,含答案)
文档属性
| 名称 | 华师大版数学九年级上册同步课时练习:23.3.3 相似三角形的性质(word,含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 100.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-18 22:23:48 | ||
图片预览



文档简介
23.3.3 相似三角形的性质
知识点 1 相似三角形对应线段的比等于相似比
1.若两个相似三角形对应角的平分线的比为5∶3,则相似比为 ,对应边上的中线的比为 ,对应边上的高的比为 .
2.在一张扩印出来的纸上,一个等腰三角形的底边长由原图中的3 cm变成了6 cm,则底边上的高由原图中的2 cm变成了 cm.
3.已知△ABC∽△A'B'C',BD和B'D'分别是△ABC的边AC和△A'B'C'的边A'C'上的高,且AB=10,A'B'=2,BD=6,求B'D'的长.
知识点 2 相似三角形周长的比等于相似比
4.因为△ABC∽△DEF,=,所以== ,则= ,所以△ABC与△DEF的周长之比为 .
5.两个相似三角形的最短边长分别为5 cm和3 cm,它们的周长之差为12 cm,那么较大三角形的周长为 ( )
A.14 cm B.16 cm C.18 cm D.30 cm
6.如图,在△ABC中,D,E分别是边AB,AC上的点,且DE∥BC.若△ADE与△ABC的周长之比为2∶3,AD=4,则DB= .
7.已知△ABC∽△A'B'C',它们的周长分别为60 cm和72 cm,且AB=15 cm,B'C'=24 cm,求AC和A'C'的长.
知识点 3 相似三角形面积的比等于相似比的平方
8.如果两个相似三角形对应边的比为2∶3,那么这两个相似三角形面积的比是( )
A.2∶3 B. C.4∶9 D.8∶27
9.若两个相似三角形的面积之比为1∶4,则它们的周长之比为 ( )
A.1∶2 B.1∶4 C.1∶5 D.1∶16
10.已知△ABC∽△DEF,且△ABC与△DEF的面积之比为9∶4,△ABC的最短边长为4.5 cm,则△DEF的最短边长为 ( )
A.6 cm B.2 cm C.3 cm D.4 cm
11.[2019·抚顺] 如果把两条直角边长分别为5,10的直角三角形按相似比进行缩小,那么得到的直角三角形的面积是 .
12.[教材练习第2题变式] 已知△ABC∽△A'B'C',=,AB边上的中线CD=4cm,△ABC的周长为20cm,△A'B'C'的面积为64 cm2.求:
(1)A'B'边上的中线C'D'的长;
(2)△A'B'C'的周长;
(3)△ABC的面积.
13.如图,△OAB∽△OCD,OA∶OC=3∶2,∠A=α,∠C=β,△OAB与△OCD的面积分别是S1和S2,△OAB与△OCD的周长分别是C1和C2,则下列等式一定成立的是 ( )
A.= B.= C.= D.=
14.如图,在平行四边形ABCD中,E为CD上一点,连结AE,BE,BD,AE,BD交于点F,若S△DEF∶S△BAF=4∶25,则DE∶EC等于 ( )
A.2∶3 B.2∶5 C.3∶5 D.3∶2
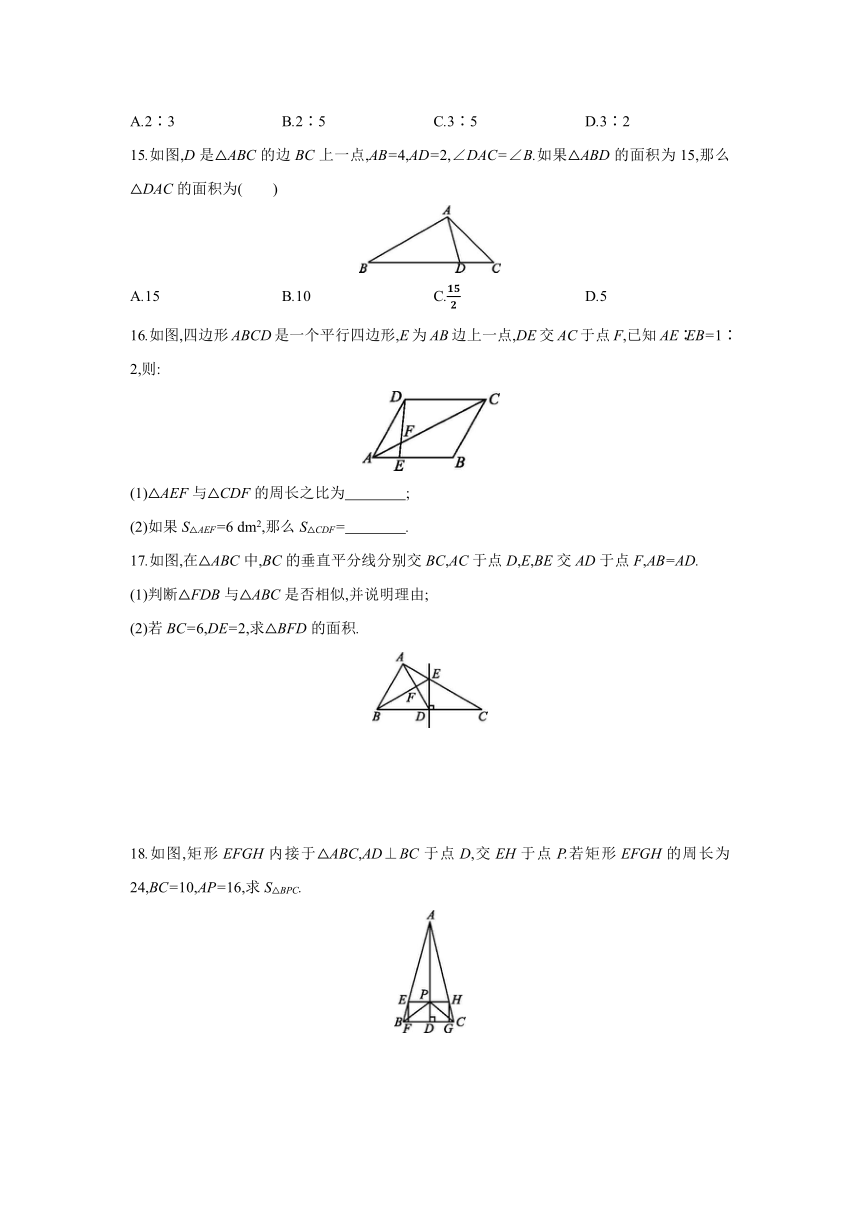
15.如图,D是△ABC的边BC上一点,AB=4,AD=2,∠DAC=∠B.如果△ABD的面积为15,那么△DAC的面积为( )
A.15 B.10 C. D.5
16.如图,四边形ABCD是一个平行四边形,E为AB边上一点,DE交AC于点F,已知AE∶EB=1∶2,则:
(1)△AEF与△CDF的周长之比为 ;
(2)如果S△AEF=6 dm2,那么S△CDF= .
17.如图,在△ABC中,BC的垂直平分线分别交BC,AC于点D,E,BE交AD于点F,AB=AD.
(1)判断△FDB与△ABC是否相似,并说明理由;
(2)若BC=6,DE=2,求△BFD的面积.
18.如图,矩形EFGH内接于△ABC,AD⊥BC于点D,交EH于点P.若矩形EFGH的周长为24,BC=10,AP=16,求S△BPC.
答案
1.5∶3 5∶3 5∶3
2.4
3.解:由题意知=,∴=,
解得B'D'=1.2.
4.EF DF DE EF DF
5.D 根据题意得两三角形的周长的比为5∶3,设两三角形的周长分别为5x cm,3x cm,则5x-3x=12,解得x=6,所以5x=30,即较大三角形的周长为30 cm.故选D.
6.2 ∵DE∥BC,
∴△ADE∽△ABC.
∵△ADE与△ABC的周长之比为2∶3,
∴AD∶AB=2∶3.
∵AD=4,∴AB=6,
∴DB=AB-AD=2.
故答案为2.
7.解:因为△ABC∽△A'B'C',
所以===.
又因为AB=15 cm,B'C'=24 cm,
所以==,
所以A'B'=18(cm),BC=20(cm),
所以AC=60-15-20=25(cm),A'C'=72-18-24=30(cm).
8.C 9.A
10.C 设△DEF的最短边长是x cm.∵△ABC∽△DEF,且面积之比为9∶4,∴△ABC与△DEF的对应边之比为3∶2,∴4.5∶x=3∶2,解得x=3.故选C.
11.9 由题意可知原三角形的面积=×5×10=25.因为两三角形相似,所以=()2=,所以缩小后的直角三角形的面积为9.故答案为9.
12.解:(1)∵=,∴=,
∴C'D'=8(cm).
(2)∵=,∴=,
∴C△A'B'C'=40(cm).
(3)∵=,∴=,
∴S△ABC=16(cm2).
13.D ∵△OAB∽△OCD,OA∶OC=3∶2,∠A=α,∠C=β,
∴=,α=β,=()2=,=.
故选D.
14.A ∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,
∴△DEF∽△BAF.
∵S△DEF∶S△BAF=4∶25,∴DE∶AB=2∶5.
∵AB=CD,∴DE∶CD=2∶5,
∴DE∶EC=2∶3.
故选A.
15.D ∵∠DAC=∠B,∠C=∠C,
∴△DAC∽△ABC.
∵AB=4,AD=2,
∴==,
∴=.
又∵△ABD的面积为15,
∴△DAC的面积为5.故选D.
16.(1)1∶3 (2)54 dm2
(1)∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴△AEF∽△CDF.
∵AE∶EB=1∶2,
∴AE∶CD=1∶3,
∴△AEF和△CDF的周长之比为1∶3.
(2)∵△AEF∽△CDF,
∴△AEF与△CDF的面积之比等于对应边长之比的平方,
即=()2=()2=.
∵S△AEF=6 dm2,∴S△CDF=54 dm2.
17.解:(1)相似.
理由:∵DE是BC的垂直平分线,
∴BE=CE,
∴∠EBC=∠ECB.
∵AB=AD,
∴∠ABC=∠ADB,
∴△FDB∽△ABC.
(2)∵DE垂直平分BC,
∴DB=BC.
∵△FDB∽△ABC,
∴==,
∴AB=2FD.
∵AB=AD,
∴AD=2FD,
∴FD=AF,
∴S△AFB=S△BFD,S△AEF=S△EFD,
∴S△ABC=3S△BDE=3××3×2=9.
∵△FDB∽△ABC,
∴=()2=()2=,
∴S△BFD=S△ABC=×9=.
18.解:设PD=x,则EF=x.
∵矩形EFGH的周长为24,
∴EF+EH=12,
∴EH=12-x.
∵EH∥BC,
∴△AEH∽△ABC,
∴=,即=,
解得x1=4,x2=-8(不合题意,舍去),
∴x=4,即PD=4,
∴S△BPC=BC·PD=×10×4=20.
知识点 1 相似三角形对应线段的比等于相似比
1.若两个相似三角形对应角的平分线的比为5∶3,则相似比为 ,对应边上的中线的比为 ,对应边上的高的比为 .
2.在一张扩印出来的纸上,一个等腰三角形的底边长由原图中的3 cm变成了6 cm,则底边上的高由原图中的2 cm变成了 cm.
3.已知△ABC∽△A'B'C',BD和B'D'分别是△ABC的边AC和△A'B'C'的边A'C'上的高,且AB=10,A'B'=2,BD=6,求B'D'的长.
知识点 2 相似三角形周长的比等于相似比
4.因为△ABC∽△DEF,=,所以== ,则= ,所以△ABC与△DEF的周长之比为 .
5.两个相似三角形的最短边长分别为5 cm和3 cm,它们的周长之差为12 cm,那么较大三角形的周长为 ( )
A.14 cm B.16 cm C.18 cm D.30 cm
6.如图,在△ABC中,D,E分别是边AB,AC上的点,且DE∥BC.若△ADE与△ABC的周长之比为2∶3,AD=4,则DB= .
7.已知△ABC∽△A'B'C',它们的周长分别为60 cm和72 cm,且AB=15 cm,B'C'=24 cm,求AC和A'C'的长.
知识点 3 相似三角形面积的比等于相似比的平方
8.如果两个相似三角形对应边的比为2∶3,那么这两个相似三角形面积的比是( )
A.2∶3 B. C.4∶9 D.8∶27
9.若两个相似三角形的面积之比为1∶4,则它们的周长之比为 ( )
A.1∶2 B.1∶4 C.1∶5 D.1∶16
10.已知△ABC∽△DEF,且△ABC与△DEF的面积之比为9∶4,△ABC的最短边长为4.5 cm,则△DEF的最短边长为 ( )
A.6 cm B.2 cm C.3 cm D.4 cm
11.[2019·抚顺] 如果把两条直角边长分别为5,10的直角三角形按相似比进行缩小,那么得到的直角三角形的面积是 .
12.[教材练习第2题变式] 已知△ABC∽△A'B'C',=,AB边上的中线CD=4cm,△ABC的周长为20cm,△A'B'C'的面积为64 cm2.求:
(1)A'B'边上的中线C'D'的长;
(2)△A'B'C'的周长;
(3)△ABC的面积.
13.如图,△OAB∽△OCD,OA∶OC=3∶2,∠A=α,∠C=β,△OAB与△OCD的面积分别是S1和S2,△OAB与△OCD的周长分别是C1和C2,则下列等式一定成立的是 ( )
A.= B.= C.= D.=
14.如图,在平行四边形ABCD中,E为CD上一点,连结AE,BE,BD,AE,BD交于点F,若S△DEF∶S△BAF=4∶25,则DE∶EC等于 ( )
A.2∶3 B.2∶5 C.3∶5 D.3∶2
15.如图,D是△ABC的边BC上一点,AB=4,AD=2,∠DAC=∠B.如果△ABD的面积为15,那么△DAC的面积为( )
A.15 B.10 C. D.5
16.如图,四边形ABCD是一个平行四边形,E为AB边上一点,DE交AC于点F,已知AE∶EB=1∶2,则:
(1)△AEF与△CDF的周长之比为 ;
(2)如果S△AEF=6 dm2,那么S△CDF= .
17.如图,在△ABC中,BC的垂直平分线分别交BC,AC于点D,E,BE交AD于点F,AB=AD.
(1)判断△FDB与△ABC是否相似,并说明理由;
(2)若BC=6,DE=2,求△BFD的面积.
18.如图,矩形EFGH内接于△ABC,AD⊥BC于点D,交EH于点P.若矩形EFGH的周长为24,BC=10,AP=16,求S△BPC.
答案
1.5∶3 5∶3 5∶3
2.4
3.解:由题意知=,∴=,
解得B'D'=1.2.
4.EF DF DE EF DF
5.D 根据题意得两三角形的周长的比为5∶3,设两三角形的周长分别为5x cm,3x cm,则5x-3x=12,解得x=6,所以5x=30,即较大三角形的周长为30 cm.故选D.
6.2 ∵DE∥BC,
∴△ADE∽△ABC.
∵△ADE与△ABC的周长之比为2∶3,
∴AD∶AB=2∶3.
∵AD=4,∴AB=6,
∴DB=AB-AD=2.
故答案为2.
7.解:因为△ABC∽△A'B'C',
所以===.
又因为AB=15 cm,B'C'=24 cm,
所以==,
所以A'B'=18(cm),BC=20(cm),
所以AC=60-15-20=25(cm),A'C'=72-18-24=30(cm).
8.C 9.A
10.C 设△DEF的最短边长是x cm.∵△ABC∽△DEF,且面积之比为9∶4,∴△ABC与△DEF的对应边之比为3∶2,∴4.5∶x=3∶2,解得x=3.故选C.
11.9 由题意可知原三角形的面积=×5×10=25.因为两三角形相似,所以=()2=,所以缩小后的直角三角形的面积为9.故答案为9.
12.解:(1)∵=,∴=,
∴C'D'=8(cm).
(2)∵=,∴=,
∴C△A'B'C'=40(cm).
(3)∵=,∴=,
∴S△ABC=16(cm2).
13.D ∵△OAB∽△OCD,OA∶OC=3∶2,∠A=α,∠C=β,
∴=,α=β,=()2=,=.
故选D.
14.A ∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,
∴△DEF∽△BAF.
∵S△DEF∶S△BAF=4∶25,∴DE∶AB=2∶5.
∵AB=CD,∴DE∶CD=2∶5,
∴DE∶EC=2∶3.
故选A.
15.D ∵∠DAC=∠B,∠C=∠C,
∴△DAC∽△ABC.
∵AB=4,AD=2,
∴==,
∴=.
又∵△ABD的面积为15,
∴△DAC的面积为5.故选D.
16.(1)1∶3 (2)54 dm2
(1)∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴△AEF∽△CDF.
∵AE∶EB=1∶2,
∴AE∶CD=1∶3,
∴△AEF和△CDF的周长之比为1∶3.
(2)∵△AEF∽△CDF,
∴△AEF与△CDF的面积之比等于对应边长之比的平方,
即=()2=()2=.
∵S△AEF=6 dm2,∴S△CDF=54 dm2.
17.解:(1)相似.
理由:∵DE是BC的垂直平分线,
∴BE=CE,
∴∠EBC=∠ECB.
∵AB=AD,
∴∠ABC=∠ADB,
∴△FDB∽△ABC.
(2)∵DE垂直平分BC,
∴DB=BC.
∵△FDB∽△ABC,
∴==,
∴AB=2FD.
∵AB=AD,
∴AD=2FD,
∴FD=AF,
∴S△AFB=S△BFD,S△AEF=S△EFD,
∴S△ABC=3S△BDE=3××3×2=9.
∵△FDB∽△ABC,
∴=()2=()2=,
∴S△BFD=S△ABC=×9=.
18.解:设PD=x,则EF=x.
∵矩形EFGH的周长为24,
∴EF+EH=12,
∴EH=12-x.
∵EH∥BC,
∴△AEH∽△ABC,
∴=,即=,
解得x1=4,x2=-8(不合题意,舍去),
∴x=4,即PD=4,
∴S△BPC=BC·PD=×10×4=20.
