华师大版数学九年级上册同步课时练习 24.2直角三角形的性质 (word版含答案)
文档属性
| 名称 | 华师大版数学九年级上册同步课时练习 24.2直角三角形的性质 (word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 147.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-19 00:00:00 | ||
图片预览


文档简介
24.2 直角三角形的性质
知识点 1 直角三角形的两个锐角互余
1.如图24-2-1,将一张矩形纸片剪去一部分后得到一个三角形,则图中∠1+∠2的度数是 ( )
A.30° B.60° C.90° D.120°
知识点 2 勾股定理
2.如图24-2-2,在△ABC中,AB=AC,AD平分∠BAC交BC边于点D.已知AB=5,AD=3,则BC的长为 ( )
A.5 B.6 C.8 D.10
3.如图24-2-3,在△ABC中,∠C=90°,D是BC边上一点,AB=17 cm,AD=10 cm,AC=8 cm,则BD的长为 .
知识点 3 直角三角形斜边上的中线的性质
4.如图24-2-4,在Rt△ABC中,E是斜边AB的中点.若AB=10,则CE= .
5.如图24-2-5,在△ABC中,∠C=2∠B,D是BC上的一点,且AD⊥AB,E是BD的中点,连结AE.求证:∠AEC=∠C.
知识点 4 含30 °角的直角三角形的性质
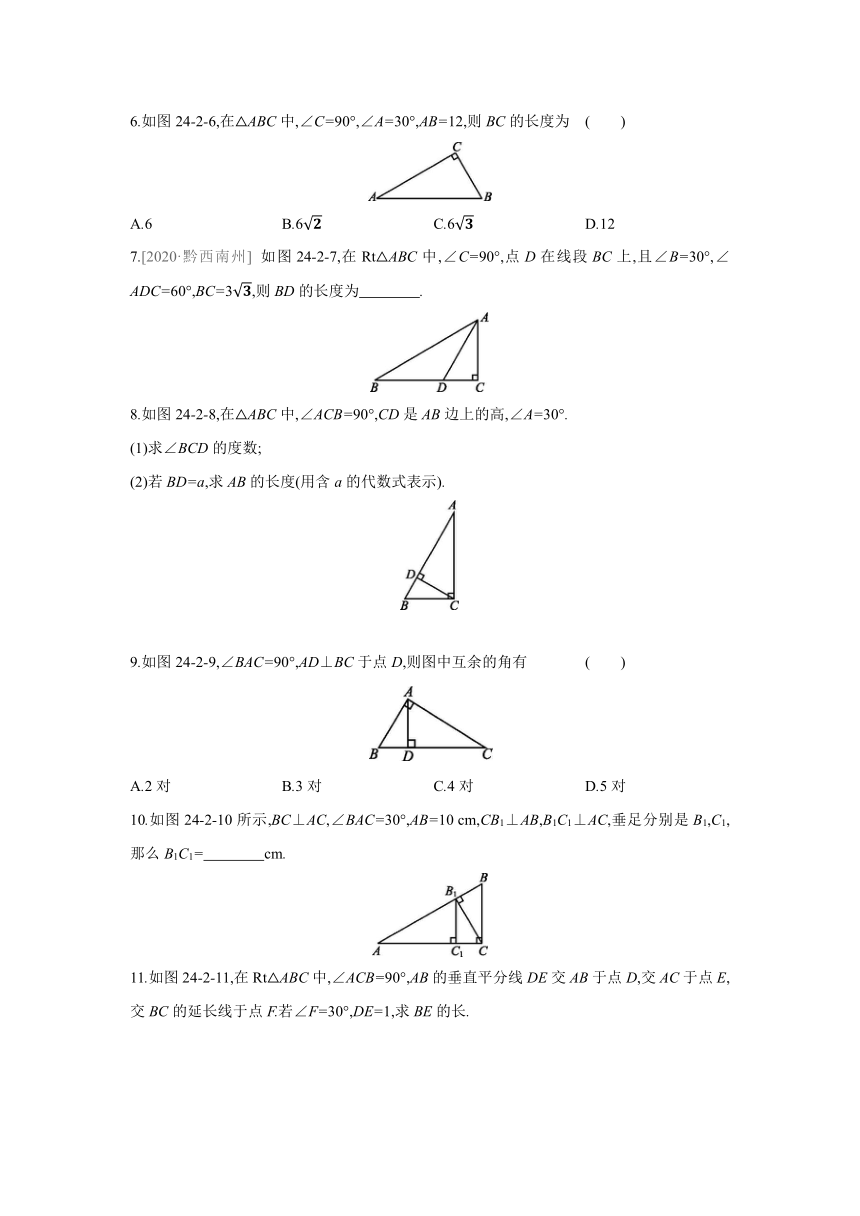
6.如图24-2-6,在△ABC中,∠C=90°,∠A=30°,AB=12,则BC的长度为 ( )
A.6 B.6 C.6 D.12
7.[2020·黔西南州] 如图24-2-7,在Rt△ABC中,∠C=90°,点D在线段BC上,且∠B=30°,∠ADC=60°,BC=3,则BD的长度为 .
8.如图24-2-8,在△ABC中,∠ACB=90°,CD是AB边上的高,∠A=30°.
(1)求∠BCD的度数;
(2)若BD=a,求AB的长度(用含a的代数式表示).
9.如图24-2-9,∠BAC=90°,AD⊥BC于点D,则图中互余的角有 ( )
A.2对 B.3对 C.4对 D.5对
10.如图24-2-10所示,BC⊥AC,∠BAC=30°,AB=10 cm,CB1⊥AB,B1C1⊥AC,垂足分别是B1,C1,那么B1C1= cm.
11.如图24-2-11,在Rt△ABC中,∠ACB=90°,AB的垂直平分线DE交AB于点D,交AC于点E,交BC的延长线于点F.若∠F=30°,DE=1,求BE的长.
12.如图24-2-12,在△ABC中,∠ACB=90°,M,N分别是AB,AC的中点,延长BC至点D,使CD=BD,连结DN,MN.
(1)求证:MN=CD;
(2)若AB=6,求DN的长.
13.如图24-2-13,已知在△ABC中,∠ACB=90°,CD为高,且CD,CE三等分∠ACB.
(1)求∠B的度数;
(2)求证:CE是AB边上的中线,且CE=AB.
14.(1)如图24-2-14①,P是∠AOB内部任意一点,PM⊥OA,PN⊥OB,垂足分别是M,N,D是OP的中点.求证:∠MDN=2∠MON.
小尧同学的思路如下:
因为PM⊥OA,垂足是M,D是OP的中点,
由“直角三角形斜边上的中线等于斜边的一半”,
得到MD=OD,…
请你帮小尧同学写出完整的证明过程.
(2)如图②,P是∠AOB外部任意一点,PM⊥OA,PN⊥OB,垂足分别是M,N,D是OP的中点.求证:∠MDN=2∠MON.
答案
1.C 2.C 3.9 cm 4.5
5.证明:∵AD⊥AB,∴△ABD为直角三角形.
∵E是BD的中点,
∴AE=BD,BE=BD,
∴AE=BE,∴∠B=∠BAE.
∵∠AEC=∠B+∠BAE,
∴∠AEC=∠B+∠B=2∠B.
又∵∠C=2∠B,∴∠AEC=∠C.
6.A
7.2
8.解:(1)∵在△ABC中,∠ACB=90°,∠A=30°,
∴∠B=60°.
∵CD是AB边上的高,∴CD⊥AB,
∴∠BDC=90°,
∴∠BCD=90°-60°=30°.
(2)∵∠BDC=90°,∠BCD=30°,BD=a,
∴BC=2BD=2a.
∵∠ACB=90°,∠A=30°,
∴AB=2BC=4a.
9.C ∵∠BAC=90°,∴∠B+∠C=90°①,∠BAD+∠CAD=90°②.∵AD⊥BC,∴∠BDA=∠CDA=90°,∴∠B+∠BAD=90°③,∠C+∠CAD=90°④.
故共4对.
10.3.75 在△ABC中,∵BC⊥AC,∠BAC=30°,AB=10 cm,
∴∠A+∠B=90°,BC=AB=5 cm.
∵CB1⊥AB,∴∠B+∠BCB1=90°,
∴∠BCB1=∠A=30°.
在Rt△BCB1中,BB1=BC=2.5 cm,
∴AB1=AB-BB1=10-2.5=7.5(cm).
在△AB1C1中,∵B1C1⊥AC,∠A=30°,
∴B1C1=AB1=×7.5=3.75(cm).
11.解:∵AB的垂直平分线DE交AB于点D,交AC于点E,交BC的延长线于点F,
∴∠BDF=90°,AE=BE,
∴∠ABE=∠A.
∵∠F=30°,∠BDF=90°,
∴∠DBF=60°.
∵∠ACB=90°,∴∠A=30°,
∴∠ABE=30°,
∴BE=2DE=2.
12. (1)根据三角形中位线定理得到MN=BC,根据题意证明;
(2)连结CM,根据平行四边形的判定定理得到四边形MCDN是平行四边形,进而得到DN=CM,再利用直角三角形的性质计算即可.
解:(1)证明:∵M,N分别是AB,AC的中点,
∴MN BC.
∵CD=BD,∴CD=BC,∴MN=CD.
(2)如图,连结CM.
由(1)知MN CD,
∴四边形MCDN是平行四边形,
∴DN=CM.
∵∠ACB=90°,M是AB的中点,
∴CM=AB,∴DN=AB=3.
13.解:(1)∵在△ABC中,∠ACB=90°,CD,CE三等分∠ACB,
∴∠ACD=∠DCE=∠BCE=30°,
∴∠BCD=60°.
又∵CD为△ABC的高,
∴∠B=90°-60°=30°.
(2)证明:由(1)知,∠B=∠BCE=30°,
∴CE=BE.
∵∠ACB=90°,∠B=30°,
∴∠A=60°.
又由(1)知∠ACD=∠DCE=30°,
∴∠ACE=60°=∠A,
∴△ACE是等边三角形,
∴AE=CE=BE=AB,即E是AB的中点,∴CE是AB边上的中线,且CE=AB.
14.证明:(1)∵PM⊥OA,D是OP的中点,
∴MD=OD,
∴∠DOM=∠DMO,
∴∠PDM=2∠AOP.
同理,∠PDN=2∠BOP,
∴∠MDN=∠PDM+∠PDN=2(∠AOP+∠BOP)=2∠MON.
(2)同(1)可得,∠PDM=2∠AOP,∠PDN=2∠BOP,
∴∠MDN=∠PDN-∠PDM=2(∠BOP-∠AOP)=2∠MON.
知识点 1 直角三角形的两个锐角互余
1.如图24-2-1,将一张矩形纸片剪去一部分后得到一个三角形,则图中∠1+∠2的度数是 ( )
A.30° B.60° C.90° D.120°
知识点 2 勾股定理
2.如图24-2-2,在△ABC中,AB=AC,AD平分∠BAC交BC边于点D.已知AB=5,AD=3,则BC的长为 ( )
A.5 B.6 C.8 D.10
3.如图24-2-3,在△ABC中,∠C=90°,D是BC边上一点,AB=17 cm,AD=10 cm,AC=8 cm,则BD的长为 .
知识点 3 直角三角形斜边上的中线的性质
4.如图24-2-4,在Rt△ABC中,E是斜边AB的中点.若AB=10,则CE= .
5.如图24-2-5,在△ABC中,∠C=2∠B,D是BC上的一点,且AD⊥AB,E是BD的中点,连结AE.求证:∠AEC=∠C.
知识点 4 含30 °角的直角三角形的性质
6.如图24-2-6,在△ABC中,∠C=90°,∠A=30°,AB=12,则BC的长度为 ( )
A.6 B.6 C.6 D.12
7.[2020·黔西南州] 如图24-2-7,在Rt△ABC中,∠C=90°,点D在线段BC上,且∠B=30°,∠ADC=60°,BC=3,则BD的长度为 .
8.如图24-2-8,在△ABC中,∠ACB=90°,CD是AB边上的高,∠A=30°.
(1)求∠BCD的度数;
(2)若BD=a,求AB的长度(用含a的代数式表示).
9.如图24-2-9,∠BAC=90°,AD⊥BC于点D,则图中互余的角有 ( )
A.2对 B.3对 C.4对 D.5对
10.如图24-2-10所示,BC⊥AC,∠BAC=30°,AB=10 cm,CB1⊥AB,B1C1⊥AC,垂足分别是B1,C1,那么B1C1= cm.
11.如图24-2-11,在Rt△ABC中,∠ACB=90°,AB的垂直平分线DE交AB于点D,交AC于点E,交BC的延长线于点F.若∠F=30°,DE=1,求BE的长.
12.如图24-2-12,在△ABC中,∠ACB=90°,M,N分别是AB,AC的中点,延长BC至点D,使CD=BD,连结DN,MN.
(1)求证:MN=CD;
(2)若AB=6,求DN的长.
13.如图24-2-13,已知在△ABC中,∠ACB=90°,CD为高,且CD,CE三等分∠ACB.
(1)求∠B的度数;
(2)求证:CE是AB边上的中线,且CE=AB.
14.(1)如图24-2-14①,P是∠AOB内部任意一点,PM⊥OA,PN⊥OB,垂足分别是M,N,D是OP的中点.求证:∠MDN=2∠MON.
小尧同学的思路如下:
因为PM⊥OA,垂足是M,D是OP的中点,
由“直角三角形斜边上的中线等于斜边的一半”,
得到MD=OD,…
请你帮小尧同学写出完整的证明过程.
(2)如图②,P是∠AOB外部任意一点,PM⊥OA,PN⊥OB,垂足分别是M,N,D是OP的中点.求证:∠MDN=2∠MON.
答案
1.C 2.C 3.9 cm 4.5
5.证明:∵AD⊥AB,∴△ABD为直角三角形.
∵E是BD的中点,
∴AE=BD,BE=BD,
∴AE=BE,∴∠B=∠BAE.
∵∠AEC=∠B+∠BAE,
∴∠AEC=∠B+∠B=2∠B.
又∵∠C=2∠B,∴∠AEC=∠C.
6.A
7.2
8.解:(1)∵在△ABC中,∠ACB=90°,∠A=30°,
∴∠B=60°.
∵CD是AB边上的高,∴CD⊥AB,
∴∠BDC=90°,
∴∠BCD=90°-60°=30°.
(2)∵∠BDC=90°,∠BCD=30°,BD=a,
∴BC=2BD=2a.
∵∠ACB=90°,∠A=30°,
∴AB=2BC=4a.
9.C ∵∠BAC=90°,∴∠B+∠C=90°①,∠BAD+∠CAD=90°②.∵AD⊥BC,∴∠BDA=∠CDA=90°,∴∠B+∠BAD=90°③,∠C+∠CAD=90°④.
故共4对.
10.3.75 在△ABC中,∵BC⊥AC,∠BAC=30°,AB=10 cm,
∴∠A+∠B=90°,BC=AB=5 cm.
∵CB1⊥AB,∴∠B+∠BCB1=90°,
∴∠BCB1=∠A=30°.
在Rt△BCB1中,BB1=BC=2.5 cm,
∴AB1=AB-BB1=10-2.5=7.5(cm).
在△AB1C1中,∵B1C1⊥AC,∠A=30°,
∴B1C1=AB1=×7.5=3.75(cm).
11.解:∵AB的垂直平分线DE交AB于点D,交AC于点E,交BC的延长线于点F,
∴∠BDF=90°,AE=BE,
∴∠ABE=∠A.
∵∠F=30°,∠BDF=90°,
∴∠DBF=60°.
∵∠ACB=90°,∴∠A=30°,
∴∠ABE=30°,
∴BE=2DE=2.
12. (1)根据三角形中位线定理得到MN=BC,根据题意证明;
(2)连结CM,根据平行四边形的判定定理得到四边形MCDN是平行四边形,进而得到DN=CM,再利用直角三角形的性质计算即可.
解:(1)证明:∵M,N分别是AB,AC的中点,
∴MN BC.
∵CD=BD,∴CD=BC,∴MN=CD.
(2)如图,连结CM.
由(1)知MN CD,
∴四边形MCDN是平行四边形,
∴DN=CM.
∵∠ACB=90°,M是AB的中点,
∴CM=AB,∴DN=AB=3.
13.解:(1)∵在△ABC中,∠ACB=90°,CD,CE三等分∠ACB,
∴∠ACD=∠DCE=∠BCE=30°,
∴∠BCD=60°.
又∵CD为△ABC的高,
∴∠B=90°-60°=30°.
(2)证明:由(1)知,∠B=∠BCE=30°,
∴CE=BE.
∵∠ACB=90°,∠B=30°,
∴∠A=60°.
又由(1)知∠ACD=∠DCE=30°,
∴∠ACE=60°=∠A,
∴△ACE是等边三角形,
∴AE=CE=BE=AB,即E是AB的中点,∴CE是AB边上的中线,且CE=AB.
14.证明:(1)∵PM⊥OA,D是OP的中点,
∴MD=OD,
∴∠DOM=∠DMO,
∴∠PDM=2∠AOP.
同理,∠PDN=2∠BOP,
∴∠MDN=∠PDM+∠PDN=2(∠AOP+∠BOP)=2∠MON.
(2)同(1)可得,∠PDM=2∠AOP,∠PDN=2∠BOP,
∴∠MDN=∠PDN-∠PDM=2(∠BOP-∠AOP)=2∠MON.
