华师大版数学九年级上册同步课时练习 24.4 解直角三角形的应用 (第2课时) (word版含答案)
文档属性
| 名称 | 华师大版数学九年级上册同步课时练习 24.4 解直角三角形的应用 (第2课时) (word版含答案) | 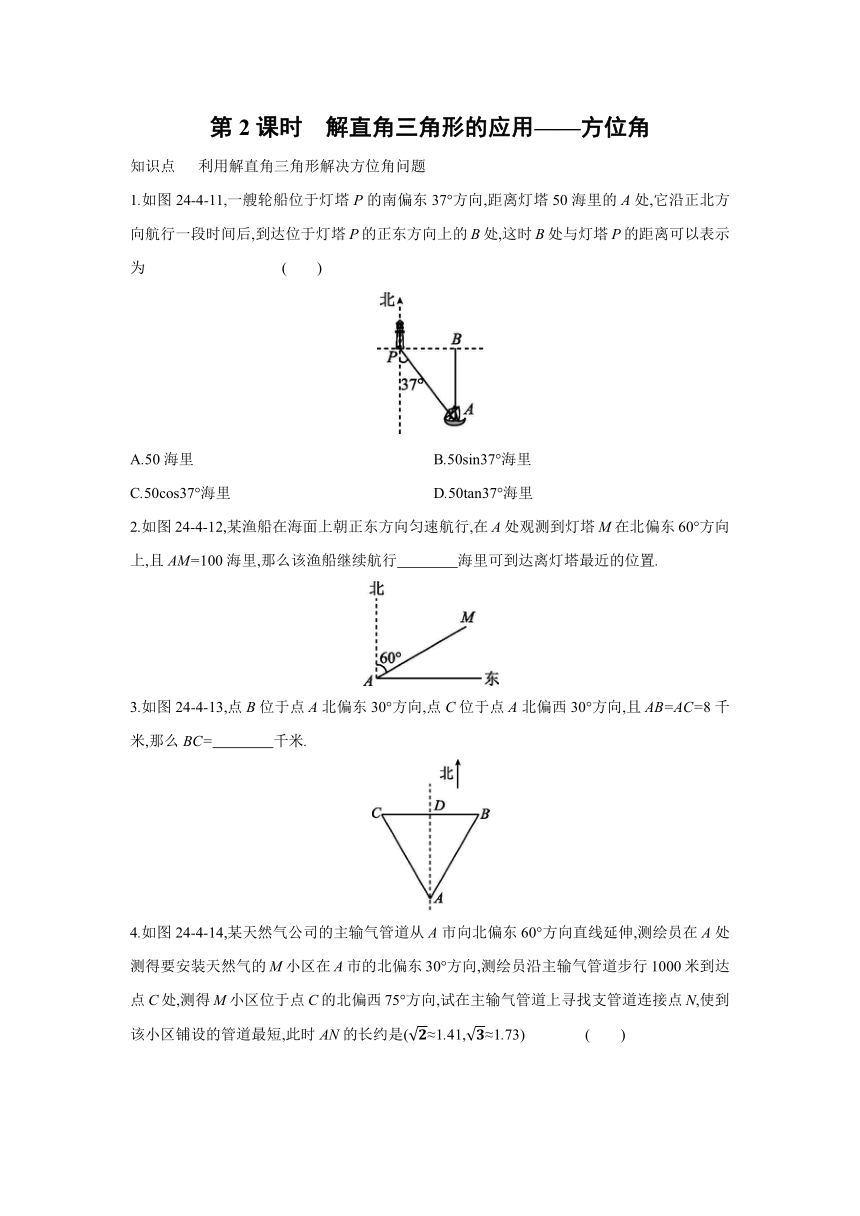 | |
| 格式 | docx | ||
| 文件大小 | 106.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-19 07:24:03 | ||
图片预览


文档简介
第2课时 解直角三角形的应用——方位角
知识点 利用解直角三角形解决方位角问题
1.如图24-4-11,一艘轮船位于灯塔P的南偏东37°方向,距离灯塔50海里的A处,它沿正北方向航行一段时间后,到达位于灯塔P的正东方向上的B处,这时B处与灯塔P的距离可以表示为 ( )
A.50海里 B.50sin37°海里
C.50cos37°海里 D.50tan37°海里
2.如图24-4-12,某渔船在海面上朝正东方向匀速航行,在A处观测到灯塔M在北偏东60°方向上,且AM=100海里,那么该渔船继续航行 海里可到达离灯塔最近的位置.
3.如图24-4-13,点B位于点A北偏东30°方向,点C位于点A北偏西30°方向,且AB=AC=8千米,那么BC= 千米.
4.如图24-4-14,某天然气公司的主输气管道从A市向北偏东60°方向直线延伸,测绘员在A处测得要安装天然气的M小区在A市的北偏东30°方向,测绘员沿主输气管道步行1000米到达点C处,测得M小区位于点C的北偏西75°方向,试在主输气管道上寻找支管道连接点N,使到该小区铺设的管道最短,此时AN的长约是(≈1.41,≈1.73) ( )
A.350米 B.650米 C.635米 D.700米
5.某节目组预设计一个新游戏:游戏线路要经过A,B,C,D四地,如图24-4-15,A,B,C三地在同一直线上,D地在A地北偏东30°方向,在C地北偏西45°方向,C地在A地北偏东75°方向,且BD=BC=40 m,则从A地到D地的距离是 m.
6.[2020·丹东] 如图24-4-16,小岛C和D都在码头O的正北方向上,它们之间的距离为6.4 km,一艘渔船自西向东匀速航行,行驶到位于码头O的正西方向A处时,测得∠CAO=26.5°,渔船速度为28 km/h,经过0.2 h,渔船行驶到了B处,测得∠DBO=49°,则渔船在B处时距离码头O有多远
(结果精确到0.1 km.参考数据:
sin26.5°≈0.45,cos26.5°≈0.89,tan26.5°≈0.50,sin49°≈0.75,cos49°≈0.66,tan49°≈1.15)
答案
1.B
2.50 如图,过点M作MN⊥AN于点N.
易知∠MAN=90°-60°=30°.
在Rt△AMN中,∵∠ANM=90°,∠MAN=30°,AM=100海里,
∴AN=AM·cos∠MAN=100×=50(海里).
故该渔船继续航行50海里可到达离灯塔最近的位置.
3.8
4.C
5.20 过点D作DE⊥BC于点E,如图所示.
由题意可知,∠DAC=75°-30°=45°,∠BCD=180°-75°-45°=60°.
∵BC=BD=40 m,
∴△BCD为等边三角形,
∴DE=BD=20 m.
在Rt△ADE中,∠AED=90°,∠DAE=45°,
∴∠ADE=45°,
∴AE=DE=20 m,
∴AD==20 m.
6.解:设渔船在B处时距离码头O有x km.
由题意知,∠O=90°.
在Rt△CAO中,∠CAO=26.5°,
∵tan∠CAO=,
∴CO=AO·tan∠CAO=(28×0.2+x)·tan26.5°≈(2.8+0.5x)km.
在Rt△DBO中,∠DBO=49°,
∵tan∠DBO=,
∴DO=BO·tan∠DBO=x·tan49°≈1.15x km.
∵DC=DO-CO,
∴6.4≈1.15x-(2.8+0.5x),
解得x≈14.2.
因此,渔船在B处时距离码头O约有14.2 km远.
知识点 利用解直角三角形解决方位角问题
1.如图24-4-11,一艘轮船位于灯塔P的南偏东37°方向,距离灯塔50海里的A处,它沿正北方向航行一段时间后,到达位于灯塔P的正东方向上的B处,这时B处与灯塔P的距离可以表示为 ( )
A.50海里 B.50sin37°海里
C.50cos37°海里 D.50tan37°海里
2.如图24-4-12,某渔船在海面上朝正东方向匀速航行,在A处观测到灯塔M在北偏东60°方向上,且AM=100海里,那么该渔船继续航行 海里可到达离灯塔最近的位置.
3.如图24-4-13,点B位于点A北偏东30°方向,点C位于点A北偏西30°方向,且AB=AC=8千米,那么BC= 千米.
4.如图24-4-14,某天然气公司的主输气管道从A市向北偏东60°方向直线延伸,测绘员在A处测得要安装天然气的M小区在A市的北偏东30°方向,测绘员沿主输气管道步行1000米到达点C处,测得M小区位于点C的北偏西75°方向,试在主输气管道上寻找支管道连接点N,使到该小区铺设的管道最短,此时AN的长约是(≈1.41,≈1.73) ( )
A.350米 B.650米 C.635米 D.700米
5.某节目组预设计一个新游戏:游戏线路要经过A,B,C,D四地,如图24-4-15,A,B,C三地在同一直线上,D地在A地北偏东30°方向,在C地北偏西45°方向,C地在A地北偏东75°方向,且BD=BC=40 m,则从A地到D地的距离是 m.
6.[2020·丹东] 如图24-4-16,小岛C和D都在码头O的正北方向上,它们之间的距离为6.4 km,一艘渔船自西向东匀速航行,行驶到位于码头O的正西方向A处时,测得∠CAO=26.5°,渔船速度为28 km/h,经过0.2 h,渔船行驶到了B处,测得∠DBO=49°,则渔船在B处时距离码头O有多远
(结果精确到0.1 km.参考数据:
sin26.5°≈0.45,cos26.5°≈0.89,tan26.5°≈0.50,sin49°≈0.75,cos49°≈0.66,tan49°≈1.15)
答案
1.B
2.50 如图,过点M作MN⊥AN于点N.
易知∠MAN=90°-60°=30°.
在Rt△AMN中,∵∠ANM=90°,∠MAN=30°,AM=100海里,
∴AN=AM·cos∠MAN=100×=50(海里).
故该渔船继续航行50海里可到达离灯塔最近的位置.
3.8
4.C
5.20 过点D作DE⊥BC于点E,如图所示.
由题意可知,∠DAC=75°-30°=45°,∠BCD=180°-75°-45°=60°.
∵BC=BD=40 m,
∴△BCD为等边三角形,
∴DE=BD=20 m.
在Rt△ADE中,∠AED=90°,∠DAE=45°,
∴∠ADE=45°,
∴AE=DE=20 m,
∴AD==20 m.
6.解:设渔船在B处时距离码头O有x km.
由题意知,∠O=90°.
在Rt△CAO中,∠CAO=26.5°,
∵tan∠CAO=,
∴CO=AO·tan∠CAO=(28×0.2+x)·tan26.5°≈(2.8+0.5x)km.
在Rt△DBO中,∠DBO=49°,
∵tan∠DBO=,
∴DO=BO·tan∠DBO=x·tan49°≈1.15x km.
∵DC=DO-CO,
∴6.4≈1.15x-(2.8+0.5x),
解得x≈14.2.
因此,渔船在B处时距离码头O约有14.2 km远.
