华师大版数学九年级上册24.3.1第1课时锐角三角函数的定义及关系应用同步课时练习(word版含答案)
文档属性
| 名称 | 华师大版数学九年级上册24.3.1第1课时锐角三角函数的定义及关系应用同步课时练习(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 143.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-19 08:06:27 | ||
图片预览


文档简介
24.3.1 第1课时 锐角三角函数的定义及关系应用
知识点 1 锐角三角函数的定义
1.如图,在Rt△ABC中,∠C=90°,AB=25,BC=7,由勾股定理,得AC====24.我们知道,在直角三角形中,锐角的正弦为对边比斜边,余弦为 比斜边,正切为 比 ,所以sinA==,cosA==,tanA==.
2.[2020·河池] 如图,在Rt△ABC中,∠C=90°,BC=5,AC=12,则sinB的值是 ( )
A. B. C. D.
3.如图,在平面直角坐标系中,点A的坐标为(4,3),那么cosα的值是 ( )
A. B. C. D.
4.如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB,垂足为D,则tan∠BCD的值是 .
5.[教材例1变式] 在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c,根据下列所给条件,分别求出∠B的三个三角函数值:
(1)a=5,b=12;
(2)a∶b=3∶4.
知识点 2 锐角三角函数之间的关系
6.如果α是锐角,且sinα=,那么cos(90°-α)的值为 ( )
A. B. C. D.
7.在Rt△ABC中,∠C=90°,下列式子不一定成立的是 ( )
A.tanA= B.sin2A+cos2A=1
C.sin2A+sin2B=1 D.tanA·tanB=1
知识点 3 锐角三角函数值的范围
8.在Rt△ABC中,∠C=90°,当∠A的度数不断增大时,cosA的值的变化情况是 ( )
A.不断增大 B.不断减小 C.不变 D.不能确定
9.若0°<α<90°,则下列说法不正确的是 ( )
A.sinα的值随α的增大而增大
B.cosα的值随α的增大而减小
C.tanα的值随α的增大而增大
D.sinα,cosα,tanα的值都随α的增大而增大
10.若∠A是锐角,sinA=3m-2,则m的取值范围是 ( )
A.C.011.如果0°<∠A<90°,并且cosA是方程(x+0.5)(x-
0.35)=0的一个根,那么cosA的值是 .
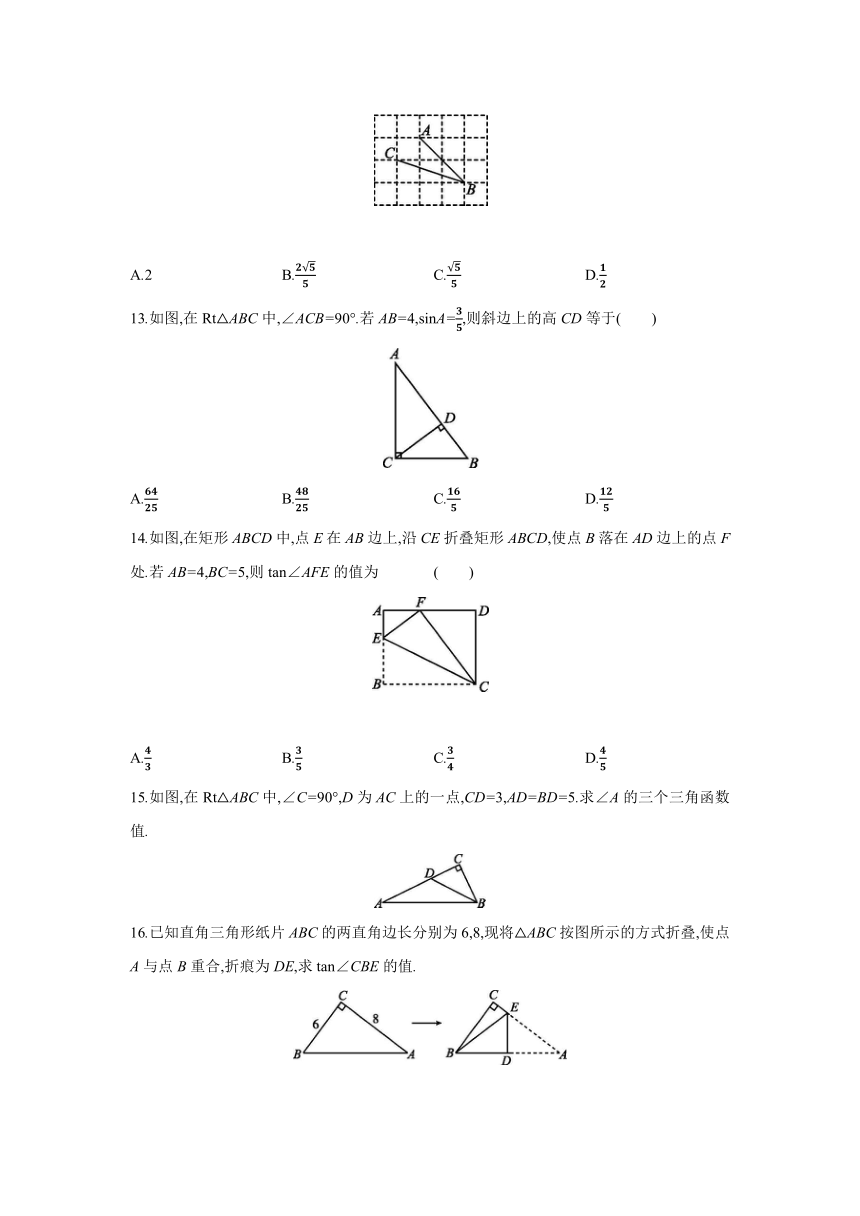
12.如图,在正方形网格中,每个小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是( )
A.2 B. C. D.
13.如图,在Rt△ABC中,∠ACB=90°.若AB=4,sinA=,则斜边上的高CD等于( )
A. B. C. D.
14.如图,在矩形ABCD中,点E在AB边上,沿CE折叠矩形ABCD,使点B落在AD边上的点F处.若AB=4,BC=5,则tan∠AFE的值为 ( )
A. B. C. D.
15.如图,在Rt△ABC中,∠C=90°,D为AC上的一点,CD=3,AD=BD=5.求∠A的三个三角函数值.
16.已知直角三角形纸片ABC的两直角边长分别为6,8,现将△ABC按图所示的方式折叠,使点A与点B重合,折痕为DE,求tan∠CBE的值.
17.在锐角三角形ABC中,AB=15,BC=14,S△ABC=84,求:
(1)tanC的值;
(2)sinA的值.
18.已知a,b,c分别为△ABC中∠A,∠B,∠C的对边,若关于x的方程(b+c)x2-2ax+c-b=0有两个相等的实数根,且sinB·cosA-cosB·sinA=0,试判断△ABC的形状.
答案
1.BC 7 49 邻边 对边 邻边 AC AB 24 25 BC AC 7 24
2.D 3.D
4. 根据题意易证∠BCD=∠A,所以tan∠BCD=tanA===.
5.解:(1)由勾股定理得c=13,
∴sinB==,cosB==,tanB==.
(2)设两直角边长分别为a=3x,b=4x,
则斜边长c==5x,
则sinB===,cosB===,
tanB===.
6.B ∵α为锐角,sinα=,∴cos(90°-α)=sinα=.故选B.
7.A
8.B 在Rt△ABC中,∠C=90°,当∠A的度数不断增大时,若斜边不变,则相邻的直角边逐渐减小,而cosA=,所以余弦值随着角度的增大(或减小)而减小(或增大).
故选B.
9.D
10.A 由题意易得0<3m-2<1,
∴11.0.35 方程的根是x1=-0.5,x2=0.35.因为0°<∠A<90°,所以012.D 如图,连结AC.
由勾股定理,得AC=,AB=2,BC=,
则BC2=AC2+AB2,
∴△ABC为直角三角形,且∠BAC=90°,
∴tan∠ABC==.故选D.
13.B ∵在Rt△ABC中,AB=4,sinA=,
∴sinA===,∴BC=.
根据勾股定理,得AC==.
∵S△ABC=AC·BC=AB·CD,
∴CD==.
14.C 易知CD=4,CF=5,由勾股定理可知DF=3,所以tan∠AFE=tan∠DCF==.
15.解:在Rt△BCD中,∵CD=3,BD=5,
∴BC===4.
又∵AC=AD+CD=8,
∴AB===4,
则sinA===,
cosA===,
tanA===.
16.解:将△ABC沿DE折叠,使点A与点B重合,则AE=BE.
设CE=x,则BE=AE=8-x.
在Rt△BCE中,由勾股定理,得BE2=CE2+BC2,即(8-x)2=x2+62,解得x=,
∴CE=,∴tan∠CBE===.
17.
解:(1)如图,过点A作AD⊥BC于点D.
∵S△ABC=BC·AD=84,
∴×14AD=84,∴AD=12.
又∵AB=15,
∴BD==9,
∴CD=14-9=5,∴tanC==.
(2)如图,过点B作BE⊥AC于点E.
由(1)知AD=12,CD=5,
∴AC==13.
∵S△ABC=AC·BE=84,∴BE=,
∴sin∠BAC==.
18.解:∵关于x的方程(b+c)x2-2ax+c-b=0有两个相等的实数根,
∴(-2a)2-4(b+c)(c-b)=0,
化简,得a2+b2-c2=0,即a2+b2=c2,
∴△ABC为直角三角形,且∠C=90°,
∴sinB=,cosA=,cosB=,sinA=.
∵sinB·cosA-cosB·sinA=0,
∴·-·=0,∴a2=b2,∴a=b,∴△ABC为等腰直角三角形.
知识点 1 锐角三角函数的定义
1.如图,在Rt△ABC中,∠C=90°,AB=25,BC=7,由勾股定理,得AC====24.我们知道,在直角三角形中,锐角的正弦为对边比斜边,余弦为 比斜边,正切为 比 ,所以sinA==,cosA==,tanA==.
2.[2020·河池] 如图,在Rt△ABC中,∠C=90°,BC=5,AC=12,则sinB的值是 ( )
A. B. C. D.
3.如图,在平面直角坐标系中,点A的坐标为(4,3),那么cosα的值是 ( )
A. B. C. D.
4.如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB,垂足为D,则tan∠BCD的值是 .
5.[教材例1变式] 在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c,根据下列所给条件,分别求出∠B的三个三角函数值:
(1)a=5,b=12;
(2)a∶b=3∶4.
知识点 2 锐角三角函数之间的关系
6.如果α是锐角,且sinα=,那么cos(90°-α)的值为 ( )
A. B. C. D.
7.在Rt△ABC中,∠C=90°,下列式子不一定成立的是 ( )
A.tanA= B.sin2A+cos2A=1
C.sin2A+sin2B=1 D.tanA·tanB=1
知识点 3 锐角三角函数值的范围
8.在Rt△ABC中,∠C=90°,当∠A的度数不断增大时,cosA的值的变化情况是 ( )
A.不断增大 B.不断减小 C.不变 D.不能确定
9.若0°<α<90°,则下列说法不正确的是 ( )
A.sinα的值随α的增大而增大
B.cosα的值随α的增大而减小
C.tanα的值随α的增大而增大
D.sinα,cosα,tanα的值都随α的增大而增大
10.若∠A是锐角,sinA=3m-2,则m的取值范围是 ( )
A.
0.35)=0的一个根,那么cosA的值是 .
12.如图,在正方形网格中,每个小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是( )
A.2 B. C. D.
13.如图,在Rt△ABC中,∠ACB=90°.若AB=4,sinA=,则斜边上的高CD等于( )
A. B. C. D.
14.如图,在矩形ABCD中,点E在AB边上,沿CE折叠矩形ABCD,使点B落在AD边上的点F处.若AB=4,BC=5,则tan∠AFE的值为 ( )
A. B. C. D.
15.如图,在Rt△ABC中,∠C=90°,D为AC上的一点,CD=3,AD=BD=5.求∠A的三个三角函数值.
16.已知直角三角形纸片ABC的两直角边长分别为6,8,现将△ABC按图所示的方式折叠,使点A与点B重合,折痕为DE,求tan∠CBE的值.
17.在锐角三角形ABC中,AB=15,BC=14,S△ABC=84,求:
(1)tanC的值;
(2)sinA的值.
18.已知a,b,c分别为△ABC中∠A,∠B,∠C的对边,若关于x的方程(b+c)x2-2ax+c-b=0有两个相等的实数根,且sinB·cosA-cosB·sinA=0,试判断△ABC的形状.
答案
1.BC 7 49 邻边 对边 邻边 AC AB 24 25 BC AC 7 24
2.D 3.D
4. 根据题意易证∠BCD=∠A,所以tan∠BCD=tanA===.
5.解:(1)由勾股定理得c=13,
∴sinB==,cosB==,tanB==.
(2)设两直角边长分别为a=3x,b=4x,
则斜边长c==5x,
则sinB===,cosB===,
tanB===.
6.B ∵α为锐角,sinα=,∴cos(90°-α)=sinα=.故选B.
7.A
8.B 在Rt△ABC中,∠C=90°,当∠A的度数不断增大时,若斜边不变,则相邻的直角边逐渐减小,而cosA=,所以余弦值随着角度的增大(或减小)而减小(或增大).
故选B.
9.D
10.A 由题意易得0<3m-2<1,
∴
由勾股定理,得AC=,AB=2,BC=,
则BC2=AC2+AB2,
∴△ABC为直角三角形,且∠BAC=90°,
∴tan∠ABC==.故选D.
13.B ∵在Rt△ABC中,AB=4,sinA=,
∴sinA===,∴BC=.
根据勾股定理,得AC==.
∵S△ABC=AC·BC=AB·CD,
∴CD==.
14.C 易知CD=4,CF=5,由勾股定理可知DF=3,所以tan∠AFE=tan∠DCF==.
15.解:在Rt△BCD中,∵CD=3,BD=5,
∴BC===4.
又∵AC=AD+CD=8,
∴AB===4,
则sinA===,
cosA===,
tanA===.
16.解:将△ABC沿DE折叠,使点A与点B重合,则AE=BE.
设CE=x,则BE=AE=8-x.
在Rt△BCE中,由勾股定理,得BE2=CE2+BC2,即(8-x)2=x2+62,解得x=,
∴CE=,∴tan∠CBE===.
17.
解:(1)如图,过点A作AD⊥BC于点D.
∵S△ABC=BC·AD=84,
∴×14AD=84,∴AD=12.
又∵AB=15,
∴BD==9,
∴CD=14-9=5,∴tanC==.
(2)如图,过点B作BE⊥AC于点E.
由(1)知AD=12,CD=5,
∴AC==13.
∵S△ABC=AC·BE=84,∴BE=,
∴sin∠BAC==.
18.解:∵关于x的方程(b+c)x2-2ax+c-b=0有两个相等的实数根,
∴(-2a)2-4(b+c)(c-b)=0,
化简,得a2+b2-c2=0,即a2+b2=c2,
∴△ABC为直角三角形,且∠C=90°,
∴sinB=,cosA=,cosB=,sinA=.
∵sinB·cosA-cosB·sinA=0,
∴·-·=0,∴a2=b2,∴a=b,∴△ABC为等腰直角三角形.
