湘教版数学七年级上册4.2 线段、射线、直线同步课时练习(word版含答案)
文档属性
| 名称 | 湘教版数学七年级上册4.2 线段、射线、直线同步课时练习(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 234.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-19 09:06:26 | ||
图片预览





文档简介
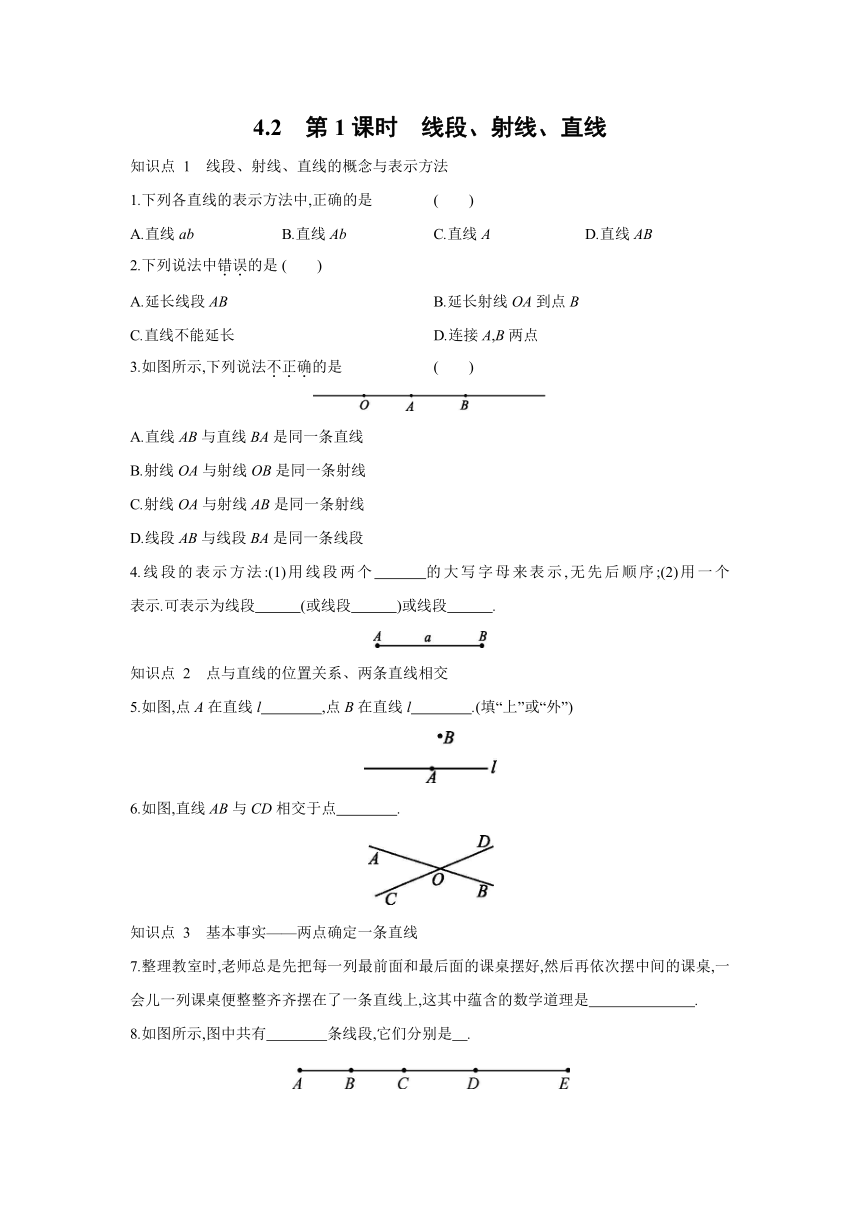
4.2 第1课时 线段、射线、直线
知识点 1 线段、射线、直线的概念与表示方法
1.下列各直线的表示方法中,正确的是 ( )
A.直线ab B.直线Ab C.直线A D.直线AB
2.下列说法中错误的是 ( )
A.延长线段AB B.延长射线OA到点B
C.直线不能延长 D.连接A,B两点
3.如图所示,下列说法不正确的是 ( )
A.直线AB与直线BA是同一条直线
B.射线OA与射线OB是同一条射线
C.射线OA与射线AB是同一条射线
D.线段AB与线段BA是同一条线段
4.线段的表示方法:(1)用线段两个 的大写字母来表示,无先后顺序;(2)用一个 表示.可表示为线段 (或线段 )或线段 .
知识点 2 点与直线的位置关系、两条直线相交
5.如图,点A在直线l ,点B在直线l .(填“上”或“外”)
6.如图,直线AB与CD相交于点 .
知识点 3 基本事实——两点确定一条直线
7.整理教室时,老师总是先把每一列最前面和最后面的课桌摆好,然后再依次摆中间的课桌,一会儿一列课桌便整整齐齐摆在了一条直线上,这其中蕴含的数学道理是 .
8.如图所示,图中共有 条线段,它们分别是 .
9.阅读下列语句,并按照这些语句画出图形.
(1)过点A和点B画直线AB;
(2)直线AB与CD相交于点C;
(3)点A在直线l上,而点B在直线l外;
(4)三条直线a,b,c都经过点M.
10.如图所示.
(1)请写出点C和直线AB,点D和直线BO的位置关系;
(2)过点A的直线共有几条 请一一写出来.
11.下表反映了平面内直线条数与它们最多交点个数的对应关系:
图形 …
直线条数 2 3 4 …
最多交点个数 1 3=1+2 6=1+2+3 …
按此规律,6条直线相交最多有多少个交点 n(n为正整数)条直线相交最多有多少个交点
第2课时 线段长短的比较
知识点 1 线段长短的比较
1.若线段AB=5 cm,CD=3 cm,则下列判断正确的是 ( )
A.AB=CD B.AB>CD C.AB2.如图,用圆规比较两条线段AB和A'B'的长短,其中正确的是 ( )
A.A'B'>AB B.A'B'=AB
C.A'B'3.如图,如图果AB=CD,那么AC与BD的长短关系是 ( )
A.AC>BD B.AC=BD C.AC知识点 2 基本事实—— 两点之间线段最短
4.如图,将一块三角形纸片剪去一部分后,发现剩余阴影部分纸片的周长要比原三角形纸片的周长大,能正确解释这一现象的数学知识是( )
A.直线没有端点,向两端无限延伸 B.两点之间线段最短
C.经过一点有无数条直线 D.两点确定一条直线
5.有下列四个生活、生产现象:①用两个钉子就可以把木条固定在墙上;②植树时,只要定出两棵树的位置,就能确定同一行树所在的直线;③从A地到B地架设电线,总是尽可能沿着线段AB架设;④把弯曲的公路改直,就能缩短路程.其中可用“两点之间线段最短”来解释的现象有 ( )
A.①② B.③④ C.①②③ D.①②③④
6.如图0所示,连接A,B两点的路径有4条,其中路径 (填序号)的路程最短.
0
知识点 3 线段的和、差与线段的中点
7.点C在线段AB上,下列条件中不能确定C是线段AB中点的是 ( )
A.AC=BC B.AC+BC=AB C.AB=2AC D.BC=AB
8.在直线l上顺次取A,B,C三点,使得AB=5 cm,BC=3 cm.如图果O是线段AC的中点,那么线段OB的长度是 ( )
A.0.5 cm B.1 cm C.1.5 cm D.2 cm
9.如图1所示,已知直线上四点A,B,C,D,看图填空:
AC= +BC=AD- ,
AC+BD-BC= .
1
10.如图2,AB=6,C为AB的中点,D为AC的中点,则BC= ,AD= .
2
11.如图3,点C,D在线段AB上,AB=48 mm,且D为BC的中点,CD=18 mm,求线段BC和AC的长.
3
知识点 4 线段的尺规作12.已知线段a,b,c(b>a>c)如图4所示.
4
求作:线段AB,使AB=a+b-c.
13.如图5,C是线段AB的中点,D是CB上一点,下列结论中错误的是 ( )
5
A.CD=AC-BD B.CD=BC
C.CD=AB-BD D.CD=AD-BC
14.[2019·岳阳期末] A,B,C是同一直线上的三个点,若AB=8 cm,BC=3 cm,则AC=
cm.
15.如图6,AB=6 cm,C是线段AB的中点,点D在CB上,且CD=DB,则AD= cm.
6
16.如图7,已知线段a,b,c,用圆规和直尺作一条线段,使它的长等于2a+b-c.
7
17.如图8,已知C为AB上一点,AC=12 cm,CB=AC,D,E分别为AC,AB的中点,求DE的长.
8
18. 如图9所示,B,C两点在线段AD上,且AB∶BC∶CD=2∶3∶4,M是AD的中点,CD=8,求MC的长.
9
19. 如图0,已知点A,B,C,D,E在同一直线上,且AC=BD,E是线段BC的中点.
(1)E是线段AD的中点吗 请说明理由;
(2)当AD=20,AB=6时,求线段BE的长.
0
20.(1)已知:如图1,点C在线段AB上,线段AC=15,BC=5,M,N分别是AC,BC的中点,求MN的长度;
(2)根据(1)的计算过程与结果,设AC+BC=a,其他条件不变,请直接写出MN的长度,并用一句简洁的语言表述你发现的规律;
(3)若把(1)中的“点C在线段AB上”改为“点C在直线AB上”,其他条件不变,结论又如图何
1
答案
1.D
2.B 射线不能延长,只能反向延长.
3.C 射线OA与射线AB的端点不同,不是同一条射线.
4.(1)端点 (2)小写字母 AB BA a
5.上 外
6.O
7.两点确定一条直线
8.10 线段AB,AC,AD,AE,BC,BD,BE,CD,CE,DE
9.解:如图图所示.
10.解:(1)点C在直线AB外,点D在直线BO上.
(2)过点A的直线共有3条,它们分别是直线AB,AC,AD.
11.解:6条直线相交最多交点个数为1+2+3+4+5=15;n条直线相交最多交点个数为.
答案
1.B
2.C 由图可知,A'B'故选C.
3.B 因为AB=CD,所以AB+BC=CD+BC,即AC=BD.故选B.
4.B
5.B ①②的理由是两点确定一条直线,③④的理由是两点之间线段最短.故选B.
6.(3) 两点之间线段最短.
7.B 选项B中C可以是线段AB上任意一点.
8.B
9.AB CD AD
10.3 因为C为AB的中点,
所以AC=BC=AB=×6=3.
因为D为AC的中点,
所以AD=AC=.
11.解:因为D为BC的中点,CD=18 mm,
所以BC=36 mm.
因为AB=48 mm,所以AC=12 mm.
12.解:作法:(1)画射线AE;
(2)在射线AE上顺次截取AC,CD,使AC=a,CD=b;
(3)在线段AD上截取线段DB,使DB=c.则线段AB就是所要求作的线段(如图图所示).
13.B 因为C是线段AB的中点,
所以AC=BC=AB.
A项,CD=BC-BD=AC-BD,故本选项正确;
B项,D不一定是BC的中点,故CD=BC不一定成立;
C项,CD=BC-BD=AB-BD,故本选项正确;
D项,CD=AD-AC=AD-BC,故本选项正确.
故选B.
14.11或5 (1)若点B在点A,C之间,AC=AB+BC=8+3=11(cm);
(2)若点C在点A,B之间,AC=AB-BC=8-3=5(cm).
所以AC的长度为11 cm或5 cm.
15.4 因为AB=6 cm,C是线段AB的中点,
所以AC=CB=AB=3 cm.
因为点D在CB上,且CD=DB,
所以CD=CB=1 cm.
所以AD=AC+CD=3+1=4(cm).
故答案为:4.
16.解:(1)作射线AF;
(2)在射线AF上顺次截取线段AB=BC=a,CD=b;
(3)在线段AD上截取DE=c.则线段AE就是所要求作的线段(如图图所示).
17.解:因为AC=12 cm,CB=AC,
所以CB=8 cm.
所以AB=AC+CB=20 cm.
因为D,E分别为AC,AB的中点,
所以AE=AB,AD=AC.
所以DE=AE-AD=(AB-AC)=4 cm,
即DE的长为4 cm.
18.解:设AB=2x,BC=3x,CD=4x,
所以AD=9x.
因为M是AD的中点,所以MD=AD=x.
因为CD=4x=8,所以x=2.
所以MC=MD-CD=x-4x=x=×2=1.
19.解:(1)E是线段AD的中点.理由如图下:
因为E是线段BC的中点,所以BE=CE.
因为AE=AC-CE,ED=BD-BE,AC=BD,
所以AE=ED.
所以E是线段AD的中点.
(2)因为AD=20,E是线段AD的中点,
所以AE=AD=10.
因为AB=6,
所以BE=AE-AB=4.
20.解:(1)因为M,N分别是AC,BC的中点,
所以MC=AC,NC=BC.
又因为AC=15,BC=5,
所以MN=MC+NC=AC+BC=(AC+BC)=10.
(2)MN=a.规律:已知线段分成两部分,这两部分的中点之间的距离等于原来线段长度的一半.
(3)分两种情况讨论:当点C在线段AB上时,由(1)得MN=AB=10;
当点C在线段AB的延长线上时,如图图,可得MN=MC-NC=AC-BC=(AC-BC)=5.
知识点 1 线段、射线、直线的概念与表示方法
1.下列各直线的表示方法中,正确的是 ( )
A.直线ab B.直线Ab C.直线A D.直线AB
2.下列说法中错误的是 ( )
A.延长线段AB B.延长射线OA到点B
C.直线不能延长 D.连接A,B两点
3.如图所示,下列说法不正确的是 ( )
A.直线AB与直线BA是同一条直线
B.射线OA与射线OB是同一条射线
C.射线OA与射线AB是同一条射线
D.线段AB与线段BA是同一条线段
4.线段的表示方法:(1)用线段两个 的大写字母来表示,无先后顺序;(2)用一个 表示.可表示为线段 (或线段 )或线段 .
知识点 2 点与直线的位置关系、两条直线相交
5.如图,点A在直线l ,点B在直线l .(填“上”或“外”)
6.如图,直线AB与CD相交于点 .
知识点 3 基本事实——两点确定一条直线
7.整理教室时,老师总是先把每一列最前面和最后面的课桌摆好,然后再依次摆中间的课桌,一会儿一列课桌便整整齐齐摆在了一条直线上,这其中蕴含的数学道理是 .
8.如图所示,图中共有 条线段,它们分别是 .
9.阅读下列语句,并按照这些语句画出图形.
(1)过点A和点B画直线AB;
(2)直线AB与CD相交于点C;
(3)点A在直线l上,而点B在直线l外;
(4)三条直线a,b,c都经过点M.
10.如图所示.
(1)请写出点C和直线AB,点D和直线BO的位置关系;
(2)过点A的直线共有几条 请一一写出来.
11.下表反映了平面内直线条数与它们最多交点个数的对应关系:
图形 …
直线条数 2 3 4 …
最多交点个数 1 3=1+2 6=1+2+3 …
按此规律,6条直线相交最多有多少个交点 n(n为正整数)条直线相交最多有多少个交点
第2课时 线段长短的比较
知识点 1 线段长短的比较
1.若线段AB=5 cm,CD=3 cm,则下列判断正确的是 ( )
A.AB=CD B.AB>CD C.AB
A.A'B'>AB B.A'B'=AB
C.A'B'
A.AC>BD B.AC=BD C.AC
4.如图,将一块三角形纸片剪去一部分后,发现剩余阴影部分纸片的周长要比原三角形纸片的周长大,能正确解释这一现象的数学知识是( )
A.直线没有端点,向两端无限延伸 B.两点之间线段最短
C.经过一点有无数条直线 D.两点确定一条直线
5.有下列四个生活、生产现象:①用两个钉子就可以把木条固定在墙上;②植树时,只要定出两棵树的位置,就能确定同一行树所在的直线;③从A地到B地架设电线,总是尽可能沿着线段AB架设;④把弯曲的公路改直,就能缩短路程.其中可用“两点之间线段最短”来解释的现象有 ( )
A.①② B.③④ C.①②③ D.①②③④
6.如图0所示,连接A,B两点的路径有4条,其中路径 (填序号)的路程最短.
0
知识点 3 线段的和、差与线段的中点
7.点C在线段AB上,下列条件中不能确定C是线段AB中点的是 ( )
A.AC=BC B.AC+BC=AB C.AB=2AC D.BC=AB
8.在直线l上顺次取A,B,C三点,使得AB=5 cm,BC=3 cm.如图果O是线段AC的中点,那么线段OB的长度是 ( )
A.0.5 cm B.1 cm C.1.5 cm D.2 cm
9.如图1所示,已知直线上四点A,B,C,D,看图填空:
AC= +BC=AD- ,
AC+BD-BC= .
1
10.如图2,AB=6,C为AB的中点,D为AC的中点,则BC= ,AD= .
2
11.如图3,点C,D在线段AB上,AB=48 mm,且D为BC的中点,CD=18 mm,求线段BC和AC的长.
3
知识点 4 线段的尺规作12.已知线段a,b,c(b>a>c)如图4所示.
4
求作:线段AB,使AB=a+b-c.
13.如图5,C是线段AB的中点,D是CB上一点,下列结论中错误的是 ( )
5
A.CD=AC-BD B.CD=BC
C.CD=AB-BD D.CD=AD-BC
14.[2019·岳阳期末] A,B,C是同一直线上的三个点,若AB=8 cm,BC=3 cm,则AC=
cm.
15.如图6,AB=6 cm,C是线段AB的中点,点D在CB上,且CD=DB,则AD= cm.
6
16.如图7,已知线段a,b,c,用圆规和直尺作一条线段,使它的长等于2a+b-c.
7
17.如图8,已知C为AB上一点,AC=12 cm,CB=AC,D,E分别为AC,AB的中点,求DE的长.
8
18. 如图9所示,B,C两点在线段AD上,且AB∶BC∶CD=2∶3∶4,M是AD的中点,CD=8,求MC的长.
9
19. 如图0,已知点A,B,C,D,E在同一直线上,且AC=BD,E是线段BC的中点.
(1)E是线段AD的中点吗 请说明理由;
(2)当AD=20,AB=6时,求线段BE的长.
0
20.(1)已知:如图1,点C在线段AB上,线段AC=15,BC=5,M,N分别是AC,BC的中点,求MN的长度;
(2)根据(1)的计算过程与结果,设AC+BC=a,其他条件不变,请直接写出MN的长度,并用一句简洁的语言表述你发现的规律;
(3)若把(1)中的“点C在线段AB上”改为“点C在直线AB上”,其他条件不变,结论又如图何
1
答案
1.D
2.B 射线不能延长,只能反向延长.
3.C 射线OA与射线AB的端点不同,不是同一条射线.
4.(1)端点 (2)小写字母 AB BA a
5.上 外
6.O
7.两点确定一条直线
8.10 线段AB,AC,AD,AE,BC,BD,BE,CD,CE,DE
9.解:如图图所示.
10.解:(1)点C在直线AB外,点D在直线BO上.
(2)过点A的直线共有3条,它们分别是直线AB,AC,AD.
11.解:6条直线相交最多交点个数为1+2+3+4+5=15;n条直线相交最多交点个数为.
答案
1.B
2.C 由图可知,A'B'
3.B 因为AB=CD,所以AB+BC=CD+BC,即AC=BD.故选B.
4.B
5.B ①②的理由是两点确定一条直线,③④的理由是两点之间线段最短.故选B.
6.(3) 两点之间线段最短.
7.B 选项B中C可以是线段AB上任意一点.
8.B
9.AB CD AD
10.3 因为C为AB的中点,
所以AC=BC=AB=×6=3.
因为D为AC的中点,
所以AD=AC=.
11.解:因为D为BC的中点,CD=18 mm,
所以BC=36 mm.
因为AB=48 mm,所以AC=12 mm.
12.解:作法:(1)画射线AE;
(2)在射线AE上顺次截取AC,CD,使AC=a,CD=b;
(3)在线段AD上截取线段DB,使DB=c.则线段AB就是所要求作的线段(如图图所示).
13.B 因为C是线段AB的中点,
所以AC=BC=AB.
A项,CD=BC-BD=AC-BD,故本选项正确;
B项,D不一定是BC的中点,故CD=BC不一定成立;
C项,CD=BC-BD=AB-BD,故本选项正确;
D项,CD=AD-AC=AD-BC,故本选项正确.
故选B.
14.11或5 (1)若点B在点A,C之间,AC=AB+BC=8+3=11(cm);
(2)若点C在点A,B之间,AC=AB-BC=8-3=5(cm).
所以AC的长度为11 cm或5 cm.
15.4 因为AB=6 cm,C是线段AB的中点,
所以AC=CB=AB=3 cm.
因为点D在CB上,且CD=DB,
所以CD=CB=1 cm.
所以AD=AC+CD=3+1=4(cm).
故答案为:4.
16.解:(1)作射线AF;
(2)在射线AF上顺次截取线段AB=BC=a,CD=b;
(3)在线段AD上截取DE=c.则线段AE就是所要求作的线段(如图图所示).
17.解:因为AC=12 cm,CB=AC,
所以CB=8 cm.
所以AB=AC+CB=20 cm.
因为D,E分别为AC,AB的中点,
所以AE=AB,AD=AC.
所以DE=AE-AD=(AB-AC)=4 cm,
即DE的长为4 cm.
18.解:设AB=2x,BC=3x,CD=4x,
所以AD=9x.
因为M是AD的中点,所以MD=AD=x.
因为CD=4x=8,所以x=2.
所以MC=MD-CD=x-4x=x=×2=1.
19.解:(1)E是线段AD的中点.理由如图下:
因为E是线段BC的中点,所以BE=CE.
因为AE=AC-CE,ED=BD-BE,AC=BD,
所以AE=ED.
所以E是线段AD的中点.
(2)因为AD=20,E是线段AD的中点,
所以AE=AD=10.
因为AB=6,
所以BE=AE-AB=4.
20.解:(1)因为M,N分别是AC,BC的中点,
所以MC=AC,NC=BC.
又因为AC=15,BC=5,
所以MN=MC+NC=AC+BC=(AC+BC)=10.
(2)MN=a.规律:已知线段分成两部分,这两部分的中点之间的距离等于原来线段长度的一半.
(3)分两种情况讨论:当点C在线段AB上时,由(1)得MN=AB=10;
当点C在线段AB的延长线上时,如图图,可得MN=MC-NC=AC-BC=(AC-BC)=5.
同课章节目录
