湘教版数学八年级上册同步课时练习:2.3 等腰三角形(含答案)
文档属性
| 名称 | 湘教版数学八年级上册同步课时练习:2.3 等腰三角形(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 241.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-19 14:52:25 | ||
图片预览


文档简介
2.3 第1课时 等腰三角形及其性质
知识点 1 等腰三角形的性质
1.等腰三角形是轴对称图形,它的对称轴有 ( )
A.3条 B.2条
C.1条 D.不能确定
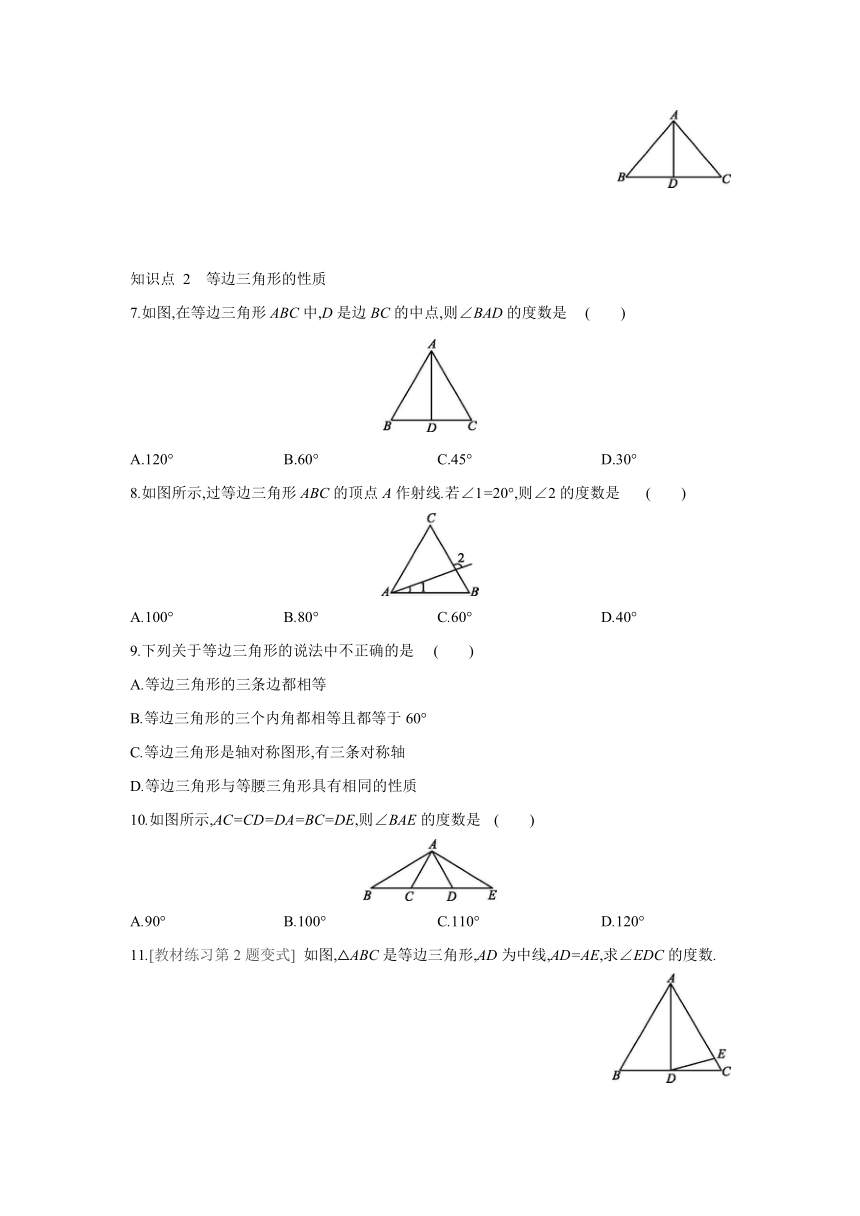
2.如图,在△ABC中,AB=AC,∠B=40°,则∠C的度数为 ( )
A.20° B.40° C.80° D.100°
3.如图所示,在△ABC中,AB=AC,BD=DC,则下列结论中错误的是 ( )
A.∠BAC=∠B B.∠1=∠2
C.AD⊥BC D.∠B=∠C
4.如图所示,在△ABC中,∠BAC=120°,AB=AC,AD⊥BC,垂足为D,则∠BAD的度数是
.
5.[2020·黄冈] 已知:如图,在△ABC中,点D在边BC上,AB=AD=DC,∠C=35°,则∠BAD=
°.
6.[教材练习第1题变式] 已知:如图,在△ABC中,AB=AC,AD平分∠BAC交BC于点D,∠B=50°,DB=6.
求:(1)BC的长;
(2)∠BAD的度数.
知识点 2 等边三角形的性质
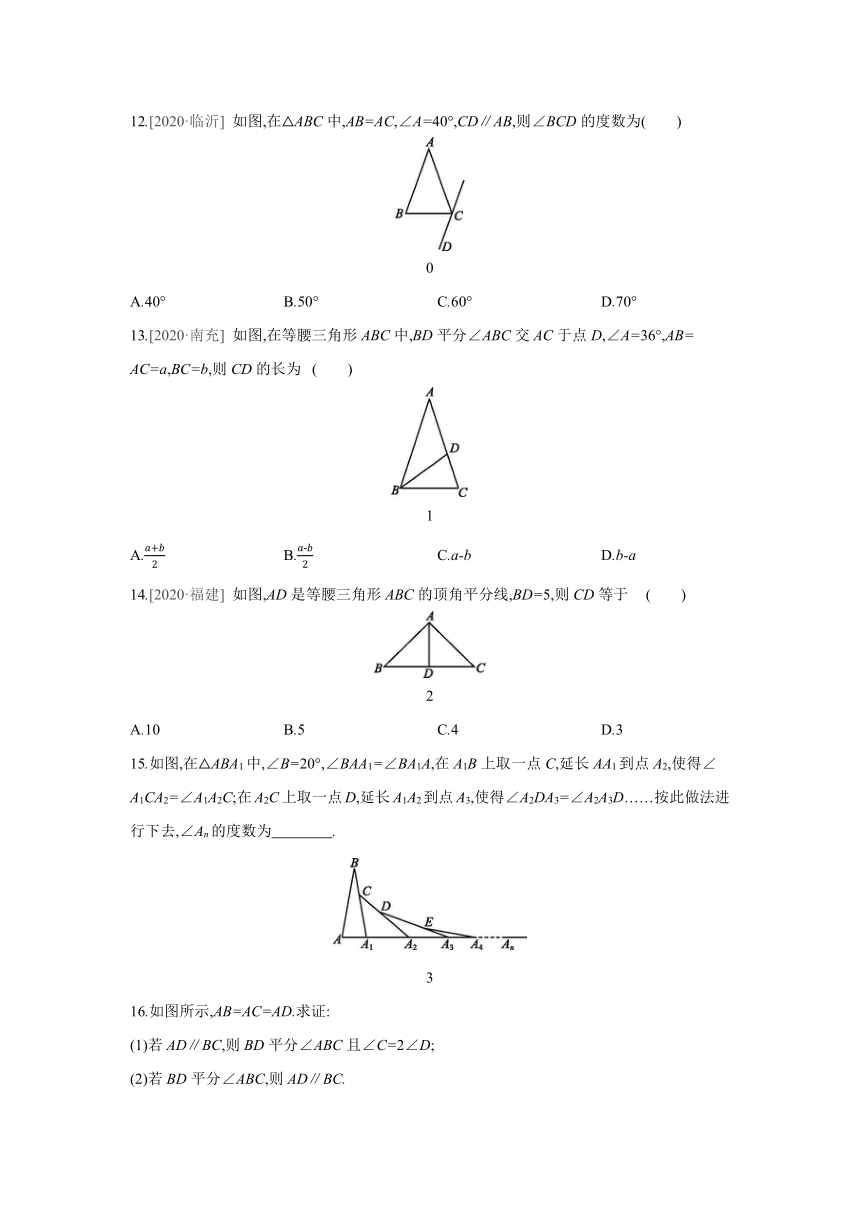
7.如图,在等边三角形ABC中,D是边BC的中点,则∠BAD的度数是 ( )
A.120° B.60° C.45° D.30°
8.如图所示,过等边三角形ABC的顶点A作射线.若∠1=20°,则∠2的度数是 ( )
A.100° B.80° C.60° D.40°
9.下列关于等边三角形的说法中不正确的是 ( )
A.等边三角形的三条边都相等
B.等边三角形的三个内角都相等且都等于60°
C.等边三角形是轴对称图形,有三条对称轴
D.等边三角形与等腰三角形具有相同的性质
10.如图所示,AC=CD=DA=BC=DE,则∠BAE的度数是 ( )
A.90° B.100° C.110° D.120°
11.[教材练习第2题变式] 如图,△ABC是等边三角形,AD为中线,AD=AE,求∠EDC的度数.
12.[2020·临沂] 如图,在△ABC中,AB=AC,∠A=40°,CD∥AB,则∠BCD的度数为( )
0
A.40° B.50° C.60° D.70°
13.[2020·南充] 如图,在等腰三角形ABC中,BD平分∠ABC交AC于点D,∠A=36°,AB=
AC=a,BC=b,则CD的长为 ( )
1
A. B. C.a-b D.b-a
14.[2020·福建] 如图,AD是等腰三角形ABC的顶角平分线,BD=5,则CD等于 ( )
2
A.10 B.5 C.4 D.3
15.如图,在△ABA1中,∠B=20°,∠BAA1=∠BA1A,在A1B上取一点C,延长AA1到点A2,使得∠A1CA2=∠A1A2C;在A2C上取一点D,延长A1A2到点A3,使得∠A2DA3=∠A2A3D……按此做法进行下去,∠An的度数为 .
3
16.如图所示,AB=AC=AD.求证:
(1)若AD∥BC,则BD平分∠ABC且∠C=2∠D;
(2)若BD平分∠ABC,则AD∥BC.
4
17.[2020·绍兴] 问题:如图,在△ABD中,BA=BD.在BD的延长线上取点E,C,作△AEC,使EA=EC.若∠BAE=90°,∠B=45°,求∠DAC的度数.
答案:∠DAC=45°.
思考:(1)如图果把以上“问题”中的条件“∠B=45°”去掉,其余条件不变,那么∠DAC的度数会改变吗 说明理由.
(2)如图果把以上“问题”中的条件“∠B=45°”去掉,再将“∠BAE=90°”改为“∠BAE=n°”,其余条件不变,求∠DAC的度数.
5
第2课时 等腰三角形的判定
知识点 1 等腰三角形的判定
1.在△ABC中,已知∠A=20°,∠B=80°,则△ABC是 ( )
A.直角三角形 B.等腰三角形
C.等边三角形 D.不能确定是何种三角形
2.若一个三角形三个内角的度数之比为2∶2∶4,则关于这个三角形的形状,下列描述最准确的是 ( )
A.等腰三角形 B.等边三角形
C.直角三角形 D.等腰直角三角形
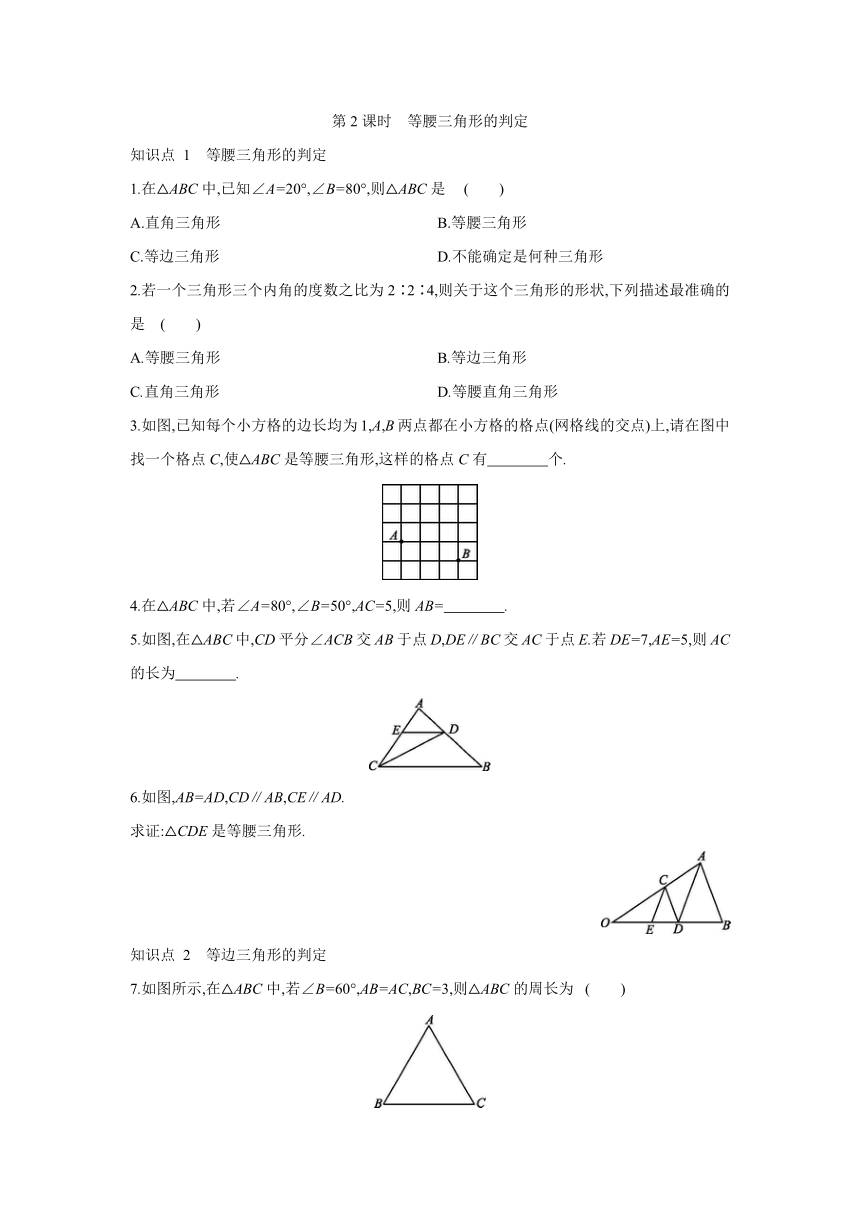
3.如图,已知每个小方格的边长均为1,A,B两点都在小方格的格点(网格线的交点)上,请在图中找一个格点C,使△ABC是等腰三角形,这样的格点C有 个.
4.在△ABC中,若∠A=80°,∠B=50°,AC=5,则AB= .
5.如图,在△ABC中,CD平分∠ACB交AB于点D,DE∥BC交AC于点E.若DE=7,AE=5,则AC的长为 .
6.如图,AB=AD,CD∥AB,CE∥AD.
求证:△CDE是等腰三角形.
知识点 2 等边三角形的判定
7.如图所示,在△ABC中,若∠B=60°,AB=AC,BC=3,则△ABC的周长为 ( )
A.9 B.8 C.6 D.12
8.下列三角形:①有两个角等于60°的三角形;②有一个角等于60°的等腰三角形;③三个外角(每个顶点处各取一个外角)都相等的三角形.其中是等边三角形的有 ( )
A.①②③ B.①② C.①③ D.②③
9.[2020·台州] 如图,等边三角形纸片ABC的边长为6,E,F是边BC的三等分点.分别过点E,F沿着平行于BA,CA方向各剪一刀,则剪下的△DEF的周长是 .
10.[教材例3变式] 如图,△ABC为等边三角形,DE∥BC,分别交AB,AC的反向延长线于D,E两点,则△ADE是等边三角形吗 为什么
11.如图所示,在△ABC中,∠A=36°,AB=AC,BD是△ABC的角平分线,点E在AB上,且BE=BC,则图中等腰三角形共有 ( )
A.2个 B.3个 C.4个 D.5个
12.如图所示,在下列三角形中,若AB=AC,则能被一条直线分成两个小等腰三角形的是( )
A.①②③ B.①②④ C.②③④ D.①③④
13.现有长度分别是4 cm,8 cm,10 cm的木条若干,从中任取3根木条,能拼成 个不同的等腰三角形.
14.如图所示,在△ABC中,AB=AC,D是AB上一点,过点D作DE⊥BC,垂足为E,与CA的延长线相交于点F.求证:△ADF是等腰三角形.
15.如图,D是△ABC的BC边上一点,AD=BD,∠ADC=80°.
(1)求∠B的度数;
(2)若∠BAC=70°,判断△ABC的形状,并说明理由.
16.已知:如图所示,在等腰三角形ABC中,AB=AC,AD平分∠BAC交BC于点D,E是AC延长线上一点,且CE=CD,AD=DE.
(1)求证:△ABC是等边三角形;
(2)如图果把AD改为△ABC的BC边上的中线或高(其他条件不变),请判断(1)中的结论是否仍然成立.(不要求证明)
17.如图所示,已知△ABC是边长为6 cm的等边三角形,动点P,Q同时从A,B两点出发,分别沿AB,BC方向匀速运动,其中点P运动的速度是1 cm/s,点Q运动的速度是2 cm/s,当点Q到达点C时,P,Q两点都停止运动,设运动时间为t s.解答下列问题:
(1)当点Q到达点C时,PQ与AB的位置关系如图何 请说明理由.
(2)在点P与点Q的运动过程中,△BPQ能否成为等边三角形 若能,请求出t的值;若不能,请说明理由.
答案
1.C 等腰三角形的对称轴是顶角平分线所在的直线.
2.B ∵AB=AC,∴∠B=∠C =40°.
3.A
4.60° ∵在△ABC中,∠BAC=120°,AB=AC,AD⊥BC,∴AD平分∠BAC,
∴∠BAD=∠BAC=×120°=60°.
5.40 ∵AD=DC,
∴∠DAC=∠C=35°,
∴∠ADB=∠DAC+∠C=70°.
∵AB=AD,
∴∠B=∠ADB=70°,
∴∠BAD=18DB=180°-70°-70°=40°.
故答案为40.
6.解:(1)∵AB=AC,AD平分∠BAC,
∴DC=DB=6,∴BC=12.
(2)∵AB=AC,
∴∠C=∠B=50°.
又∵∠BAC+∠B+∠C=180°,
∴∠BAC=80°.
又AD平分∠BAC,
∴∠BAD=40°.
7.D ∵△ABC是等边三角形,∴∠BAC=60°,AB=AC.
又D是边BC的中点,∴∠BAD=∠BAC=30°.
8.A 如图图,∵△ABC是等边三角形,
∴∠B=60°.
∵∠1=20°,
∴∠3=180°-20°-60°=100°.
∵∠3=∠2,∴∠2=100°.
故选A.
9.D
10.D ∵AC=CD=DA=BC=DE,∴△ACD为等边三角形,△BCA和△ADE均为等腰三角形,可知∠BAE=120°.故选D.
11.解:∵AD是等边三角形ABC的中线,
∴AD是等边三角形ABC的角平分线、高线,
∴∠ADC=90°,∠DAE=∠BAC=30°.
∵AE=AD,
∴∠AED=∠ADE==75°,
∴∠EDC=∠ADC-∠ADE=15°.
12.D ∵在△ABC中,AB=AC,∠A=40°,
∴∠B=70°.
∵CD∥AB,
∴∠BCD=∠B=70°.
故选D.
13.C ∵在等腰三角形ABC中,BD平分∠ABC,∠A=36°,
∴∠ABC=∠C=2∠ABD=72°,
∴∠ABD=36°=∠A,
∴BD=AD,
∴∠BDC=∠A+∠ABD=72°=∠C,
∴BD=BC.
∵AB=AC=a,BC=b,
∴CD=AC-AD=a-b.
故选C.
14.B ∵AD是等腰三角形ABC的顶角平分线,BD=5,∴CD=5.故选B.
15. ∵在△ABA1中,∠B=20°,∠BAA1=∠BA1A,
∴∠BA1A===80°.
∵∠A1CA2=∠A1A2C,∠BA1A是△A1A2C的外角,
∴∠A1A2C===40°;
同理可得,∠A2A3D=20°,∠A3A4E=10°,
∴∠An=.
故答案为.
16.证明:(1)∵AB=AC=AD,
∴∠ABC=∠C,∠ABD=∠D.
∵AD∥BC,
∴∠D=∠CBD,
∴∠ABD=∠CBD,
即BD平分∠ABC,
∴∠ABC=∠ABD+∠CBD=∠D+∠D=2∠D,
∴∠C=2∠D.
(2)∵BD平分∠ABC,
∴∠ABD=∠CBD.
∵AB=AD,
∴∠ABD=∠D,
∴∠CBD=∠D,
∴AD∥BC.
17.解:(1)∠DAC的度数不会改变.
理由:∵EA=EC,
∴∠CAE=∠C.①
又∵∠AED=∠CAE+∠C,
∴∠AED=2∠C.
∵BA=BD,
∴∠BAD=∠BDA.
∵∠BAE=90°,
∴∠B=90°-∠AED=90°-2∠C,
∴∠BAD=(180°-∠B)=[180°-(90°-2∠C)]=45°+∠C,
∴∠DAE=90°-∠BAD=90°-(45°+∠C)=45°-∠C.②
由①②,得∠DAC=∠DAE+∠CAE=45°-∠C+∠C=45°.
(2)设∠ABC=m°,
则∠BAD=(180°-m°)=90°-m°,∠AEB=18,
∴∠DAE=n°-∠BAD=n°-90°+m°.
∵EA=EC,
∴∠CAE=∠C.
又∵∠AEB=∠C+∠CAE=2∠CAE,
∴∠CAE=∠AEB=90°-n°-m°,
∴∠DAC=∠DAE+∠CAE=n°-90°+m°+90°-n°-m°=n°.
答案
1.B ∵∠A=20°,∠B=80°,
∴∠C=180°-80°-20°=80°,
∴∠B=∠C,
∴△ABC是等腰三角形.
2.D
3.8 如图图,使△ABC是等腰三角形的格点C有8个.故答案为8.
4.5
5.12 ∵CD平分∠ACB,
∴∠ACD=∠BCD.
∵DE∥BC,
∴∠EDC=∠BCD,∴∠ACD=∠EDC,
∴△ECD是等腰三角形,∴EC=DE.
又∵AE=5,DE=7,
∴AC=AE+EC=AE+DE=5+7=12.
6.证明:∵AB=AD,∴∠ADB=∠B.
∵CD∥AB,∴∠CDE=∠B.
∵CE∥AD,∴∠CED=∠ADB,
∴∠CED=∠CDE,
∴CE=CD,∴△CDE是等腰三角形.
7.A ∵AB=AC,∠B=60°,
∴△ABC是等边三角形.
∵BC=3,∴△ABC的周长为3×3=9.故选A.
8.A ①有两个角为60°,则第三个角也是60°,故其是等边三角形;
②有一个角等于60°的等腰三角形是等边三角形;
③三个外角相等,则三个内角相等,故其是等边三角形.
所以都正确.
故选A.
9.6 ∵等边三角形纸片ABC的边长为6,E,F是边BC的三等分点,
∴EF=2.
∵△ABC是等边三角形,
∴∠B=∠C=60°.
又∵DE∥AB,DF∥AC,
∴∠DEF=∠B=60°,∠DFE=∠C=60°,
∴△DEF是等边三角形,
∴△DEF的周长是2×3=6.
故答案为6.
10.解:△ADE是等边三角形.
理由:∵△ABC是等边三角形,
∴∠BAC=∠B=∠C=60°.
∵DE∥BC,
∴∠D=∠B=60°,∠E=∠C=60°,
∴∠E=∠D=∠EAD=60°,
∴△ADE是等边三角形.
11.D ∵AB=AC,
∴△ABC是等腰三角形.
∵AB=AC,∠A=36°,
∴∠ABC=∠C=72°.
∵BD是△ABC的角平分线,
∴∠ABD=∠DBC=∠ABC=36°,
∴∠A=∠ABD=36°,∴BD=AD,
∴△ABD是等腰三角形.
在△BCD中,∵∠BDC=180°-∠DBC-∠C=180°-36°-72°=72°,
∴∠C=∠BDC=72°,∴BD=BC,
∴△BCD是等腰三角形.
∵BE=BC,∴BD=BE,
∴△BDE是等腰三角形,
∴∠BED=(180°-36°)÷2=72°,
∴∠ADE=∠BED-∠A=72°-36°=36°,
∴∠A=∠ADE,∴DE=AE,
∴△ADE是等腰三角形.
故图中的等腰三角形共有5个.
12.D ①中,作底角的平分线即可;
②中,不能;
③中,作底边上的中线即可;
④中,在BC边上截取BD=AB即可.
故选D.
13.7 其中的任意三条组合有(4,4,4),(8,8,8),(10,10,10),(8,8,4),(8,8,10),(10,10,4),(10,10,8).故答案为7.
14.证明:∵AB=AC,
∴∠B=∠C.
∵DE⊥BC,
∴∠DEB=∠FEC=90°,
∴∠B+∠BDE=90°,∠C+∠F=90°,
∴∠BDE=∠F.
又∵∠ADF=∠BDE,
∴∠ADF=∠F,
∴AD=AF,
∴△ADF是等腰三角形.
15.解:(1)∵在△ABD中,AD=BD,
∴∠B=∠BAD.
∵∠ADC=∠B+∠BAD=80°,
∴∠B=∠ADC=40°.
(2)△ABC是等腰三角形.
理由:∵∠B=40°,∠BAC=70°,
∴∠C=18AC=70°,
∴∠C=∠BAC,
∴BA=BC,
∴△ABC是等腰三角形.
16.解:(1)证明:∵CD=CE,
∴∠E=∠CDE,
∴∠ACB=∠E+∠CDE=2∠E.
∵AD=DE,∴∠E=∠DAC.
∵AD平分∠BAC,
∴∠BAC=2∠DAC=2∠E,
∴∠ACB=∠BAC,∴AB=BC.
又∵AB=AC,∴AB=BC=AC,
∴△ABC是等边三角形.
(2)当AD为△ABC的BC边上的中线或高时,(1)中的结论仍然成立.
17.解:(1)当点Q到达点C时,PQ⊥AB.
理由:∵AB=AC=BC=6 cm,
∴当点Q到达点C时,t==3(s),
此时AP=3×1=3(cm),即P为AB的中点,
∴PQ⊥AB.
(2)能.当△BPQ为等边三角形时,BP=BQ,
∴6-t=2t,解得t=2.
∴当t=2时,△BPQ是等边三角形.
知识点 1 等腰三角形的性质
1.等腰三角形是轴对称图形,它的对称轴有 ( )
A.3条 B.2条
C.1条 D.不能确定
2.如图,在△ABC中,AB=AC,∠B=40°,则∠C的度数为 ( )
A.20° B.40° C.80° D.100°
3.如图所示,在△ABC中,AB=AC,BD=DC,则下列结论中错误的是 ( )
A.∠BAC=∠B B.∠1=∠2
C.AD⊥BC D.∠B=∠C
4.如图所示,在△ABC中,∠BAC=120°,AB=AC,AD⊥BC,垂足为D,则∠BAD的度数是
.
5.[2020·黄冈] 已知:如图,在△ABC中,点D在边BC上,AB=AD=DC,∠C=35°,则∠BAD=
°.
6.[教材练习第1题变式] 已知:如图,在△ABC中,AB=AC,AD平分∠BAC交BC于点D,∠B=50°,DB=6.
求:(1)BC的长;
(2)∠BAD的度数.
知识点 2 等边三角形的性质
7.如图,在等边三角形ABC中,D是边BC的中点,则∠BAD的度数是 ( )
A.120° B.60° C.45° D.30°
8.如图所示,过等边三角形ABC的顶点A作射线.若∠1=20°,则∠2的度数是 ( )
A.100° B.80° C.60° D.40°
9.下列关于等边三角形的说法中不正确的是 ( )
A.等边三角形的三条边都相等
B.等边三角形的三个内角都相等且都等于60°
C.等边三角形是轴对称图形,有三条对称轴
D.等边三角形与等腰三角形具有相同的性质
10.如图所示,AC=CD=DA=BC=DE,则∠BAE的度数是 ( )
A.90° B.100° C.110° D.120°
11.[教材练习第2题变式] 如图,△ABC是等边三角形,AD为中线,AD=AE,求∠EDC的度数.
12.[2020·临沂] 如图,在△ABC中,AB=AC,∠A=40°,CD∥AB,则∠BCD的度数为( )
0
A.40° B.50° C.60° D.70°
13.[2020·南充] 如图,在等腰三角形ABC中,BD平分∠ABC交AC于点D,∠A=36°,AB=
AC=a,BC=b,则CD的长为 ( )
1
A. B. C.a-b D.b-a
14.[2020·福建] 如图,AD是等腰三角形ABC的顶角平分线,BD=5,则CD等于 ( )
2
A.10 B.5 C.4 D.3
15.如图,在△ABA1中,∠B=20°,∠BAA1=∠BA1A,在A1B上取一点C,延长AA1到点A2,使得∠A1CA2=∠A1A2C;在A2C上取一点D,延长A1A2到点A3,使得∠A2DA3=∠A2A3D……按此做法进行下去,∠An的度数为 .
3
16.如图所示,AB=AC=AD.求证:
(1)若AD∥BC,则BD平分∠ABC且∠C=2∠D;
(2)若BD平分∠ABC,则AD∥BC.
4
17.[2020·绍兴] 问题:如图,在△ABD中,BA=BD.在BD的延长线上取点E,C,作△AEC,使EA=EC.若∠BAE=90°,∠B=45°,求∠DAC的度数.
答案:∠DAC=45°.
思考:(1)如图果把以上“问题”中的条件“∠B=45°”去掉,其余条件不变,那么∠DAC的度数会改变吗 说明理由.
(2)如图果把以上“问题”中的条件“∠B=45°”去掉,再将“∠BAE=90°”改为“∠BAE=n°”,其余条件不变,求∠DAC的度数.
5
第2课时 等腰三角形的判定
知识点 1 等腰三角形的判定
1.在△ABC中,已知∠A=20°,∠B=80°,则△ABC是 ( )
A.直角三角形 B.等腰三角形
C.等边三角形 D.不能确定是何种三角形
2.若一个三角形三个内角的度数之比为2∶2∶4,则关于这个三角形的形状,下列描述最准确的是 ( )
A.等腰三角形 B.等边三角形
C.直角三角形 D.等腰直角三角形
3.如图,已知每个小方格的边长均为1,A,B两点都在小方格的格点(网格线的交点)上,请在图中找一个格点C,使△ABC是等腰三角形,这样的格点C有 个.
4.在△ABC中,若∠A=80°,∠B=50°,AC=5,则AB= .
5.如图,在△ABC中,CD平分∠ACB交AB于点D,DE∥BC交AC于点E.若DE=7,AE=5,则AC的长为 .
6.如图,AB=AD,CD∥AB,CE∥AD.
求证:△CDE是等腰三角形.
知识点 2 等边三角形的判定
7.如图所示,在△ABC中,若∠B=60°,AB=AC,BC=3,则△ABC的周长为 ( )
A.9 B.8 C.6 D.12
8.下列三角形:①有两个角等于60°的三角形;②有一个角等于60°的等腰三角形;③三个外角(每个顶点处各取一个外角)都相等的三角形.其中是等边三角形的有 ( )
A.①②③ B.①② C.①③ D.②③
9.[2020·台州] 如图,等边三角形纸片ABC的边长为6,E,F是边BC的三等分点.分别过点E,F沿着平行于BA,CA方向各剪一刀,则剪下的△DEF的周长是 .
10.[教材例3变式] 如图,△ABC为等边三角形,DE∥BC,分别交AB,AC的反向延长线于D,E两点,则△ADE是等边三角形吗 为什么
11.如图所示,在△ABC中,∠A=36°,AB=AC,BD是△ABC的角平分线,点E在AB上,且BE=BC,则图中等腰三角形共有 ( )
A.2个 B.3个 C.4个 D.5个
12.如图所示,在下列三角形中,若AB=AC,则能被一条直线分成两个小等腰三角形的是( )
A.①②③ B.①②④ C.②③④ D.①③④
13.现有长度分别是4 cm,8 cm,10 cm的木条若干,从中任取3根木条,能拼成 个不同的等腰三角形.
14.如图所示,在△ABC中,AB=AC,D是AB上一点,过点D作DE⊥BC,垂足为E,与CA的延长线相交于点F.求证:△ADF是等腰三角形.
15.如图,D是△ABC的BC边上一点,AD=BD,∠ADC=80°.
(1)求∠B的度数;
(2)若∠BAC=70°,判断△ABC的形状,并说明理由.
16.已知:如图所示,在等腰三角形ABC中,AB=AC,AD平分∠BAC交BC于点D,E是AC延长线上一点,且CE=CD,AD=DE.
(1)求证:△ABC是等边三角形;
(2)如图果把AD改为△ABC的BC边上的中线或高(其他条件不变),请判断(1)中的结论是否仍然成立.(不要求证明)
17.如图所示,已知△ABC是边长为6 cm的等边三角形,动点P,Q同时从A,B两点出发,分别沿AB,BC方向匀速运动,其中点P运动的速度是1 cm/s,点Q运动的速度是2 cm/s,当点Q到达点C时,P,Q两点都停止运动,设运动时间为t s.解答下列问题:
(1)当点Q到达点C时,PQ与AB的位置关系如图何 请说明理由.
(2)在点P与点Q的运动过程中,△BPQ能否成为等边三角形 若能,请求出t的值;若不能,请说明理由.
答案
1.C 等腰三角形的对称轴是顶角平分线所在的直线.
2.B ∵AB=AC,∴∠B=∠C =40°.
3.A
4.60° ∵在△ABC中,∠BAC=120°,AB=AC,AD⊥BC,∴AD平分∠BAC,
∴∠BAD=∠BAC=×120°=60°.
5.40 ∵AD=DC,
∴∠DAC=∠C=35°,
∴∠ADB=∠DAC+∠C=70°.
∵AB=AD,
∴∠B=∠ADB=70°,
∴∠BAD=18DB=180°-70°-70°=40°.
故答案为40.
6.解:(1)∵AB=AC,AD平分∠BAC,
∴DC=DB=6,∴BC=12.
(2)∵AB=AC,
∴∠C=∠B=50°.
又∵∠BAC+∠B+∠C=180°,
∴∠BAC=80°.
又AD平分∠BAC,
∴∠BAD=40°.
7.D ∵△ABC是等边三角形,∴∠BAC=60°,AB=AC.
又D是边BC的中点,∴∠BAD=∠BAC=30°.
8.A 如图图,∵△ABC是等边三角形,
∴∠B=60°.
∵∠1=20°,
∴∠3=180°-20°-60°=100°.
∵∠3=∠2,∴∠2=100°.
故选A.
9.D
10.D ∵AC=CD=DA=BC=DE,∴△ACD为等边三角形,△BCA和△ADE均为等腰三角形,可知∠BAE=120°.故选D.
11.解:∵AD是等边三角形ABC的中线,
∴AD是等边三角形ABC的角平分线、高线,
∴∠ADC=90°,∠DAE=∠BAC=30°.
∵AE=AD,
∴∠AED=∠ADE==75°,
∴∠EDC=∠ADC-∠ADE=15°.
12.D ∵在△ABC中,AB=AC,∠A=40°,
∴∠B=70°.
∵CD∥AB,
∴∠BCD=∠B=70°.
故选D.
13.C ∵在等腰三角形ABC中,BD平分∠ABC,∠A=36°,
∴∠ABC=∠C=2∠ABD=72°,
∴∠ABD=36°=∠A,
∴BD=AD,
∴∠BDC=∠A+∠ABD=72°=∠C,
∴BD=BC.
∵AB=AC=a,BC=b,
∴CD=AC-AD=a-b.
故选C.
14.B ∵AD是等腰三角形ABC的顶角平分线,BD=5,∴CD=5.故选B.
15. ∵在△ABA1中,∠B=20°,∠BAA1=∠BA1A,
∴∠BA1A===80°.
∵∠A1CA2=∠A1A2C,∠BA1A是△A1A2C的外角,
∴∠A1A2C===40°;
同理可得,∠A2A3D=20°,∠A3A4E=10°,
∴∠An=.
故答案为.
16.证明:(1)∵AB=AC=AD,
∴∠ABC=∠C,∠ABD=∠D.
∵AD∥BC,
∴∠D=∠CBD,
∴∠ABD=∠CBD,
即BD平分∠ABC,
∴∠ABC=∠ABD+∠CBD=∠D+∠D=2∠D,
∴∠C=2∠D.
(2)∵BD平分∠ABC,
∴∠ABD=∠CBD.
∵AB=AD,
∴∠ABD=∠D,
∴∠CBD=∠D,
∴AD∥BC.
17.解:(1)∠DAC的度数不会改变.
理由:∵EA=EC,
∴∠CAE=∠C.①
又∵∠AED=∠CAE+∠C,
∴∠AED=2∠C.
∵BA=BD,
∴∠BAD=∠BDA.
∵∠BAE=90°,
∴∠B=90°-∠AED=90°-2∠C,
∴∠BAD=(180°-∠B)=[180°-(90°-2∠C)]=45°+∠C,
∴∠DAE=90°-∠BAD=90°-(45°+∠C)=45°-∠C.②
由①②,得∠DAC=∠DAE+∠CAE=45°-∠C+∠C=45°.
(2)设∠ABC=m°,
则∠BAD=(180°-m°)=90°-m°,∠AEB=18,
∴∠DAE=n°-∠BAD=n°-90°+m°.
∵EA=EC,
∴∠CAE=∠C.
又∵∠AEB=∠C+∠CAE=2∠CAE,
∴∠CAE=∠AEB=90°-n°-m°,
∴∠DAC=∠DAE+∠CAE=n°-90°+m°+90°-n°-m°=n°.
答案
1.B ∵∠A=20°,∠B=80°,
∴∠C=180°-80°-20°=80°,
∴∠B=∠C,
∴△ABC是等腰三角形.
2.D
3.8 如图图,使△ABC是等腰三角形的格点C有8个.故答案为8.
4.5
5.12 ∵CD平分∠ACB,
∴∠ACD=∠BCD.
∵DE∥BC,
∴∠EDC=∠BCD,∴∠ACD=∠EDC,
∴△ECD是等腰三角形,∴EC=DE.
又∵AE=5,DE=7,
∴AC=AE+EC=AE+DE=5+7=12.
6.证明:∵AB=AD,∴∠ADB=∠B.
∵CD∥AB,∴∠CDE=∠B.
∵CE∥AD,∴∠CED=∠ADB,
∴∠CED=∠CDE,
∴CE=CD,∴△CDE是等腰三角形.
7.A ∵AB=AC,∠B=60°,
∴△ABC是等边三角形.
∵BC=3,∴△ABC的周长为3×3=9.故选A.
8.A ①有两个角为60°,则第三个角也是60°,故其是等边三角形;
②有一个角等于60°的等腰三角形是等边三角形;
③三个外角相等,则三个内角相等,故其是等边三角形.
所以都正确.
故选A.
9.6 ∵等边三角形纸片ABC的边长为6,E,F是边BC的三等分点,
∴EF=2.
∵△ABC是等边三角形,
∴∠B=∠C=60°.
又∵DE∥AB,DF∥AC,
∴∠DEF=∠B=60°,∠DFE=∠C=60°,
∴△DEF是等边三角形,
∴△DEF的周长是2×3=6.
故答案为6.
10.解:△ADE是等边三角形.
理由:∵△ABC是等边三角形,
∴∠BAC=∠B=∠C=60°.
∵DE∥BC,
∴∠D=∠B=60°,∠E=∠C=60°,
∴∠E=∠D=∠EAD=60°,
∴△ADE是等边三角形.
11.D ∵AB=AC,
∴△ABC是等腰三角形.
∵AB=AC,∠A=36°,
∴∠ABC=∠C=72°.
∵BD是△ABC的角平分线,
∴∠ABD=∠DBC=∠ABC=36°,
∴∠A=∠ABD=36°,∴BD=AD,
∴△ABD是等腰三角形.
在△BCD中,∵∠BDC=180°-∠DBC-∠C=180°-36°-72°=72°,
∴∠C=∠BDC=72°,∴BD=BC,
∴△BCD是等腰三角形.
∵BE=BC,∴BD=BE,
∴△BDE是等腰三角形,
∴∠BED=(180°-36°)÷2=72°,
∴∠ADE=∠BED-∠A=72°-36°=36°,
∴∠A=∠ADE,∴DE=AE,
∴△ADE是等腰三角形.
故图中的等腰三角形共有5个.
12.D ①中,作底角的平分线即可;
②中,不能;
③中,作底边上的中线即可;
④中,在BC边上截取BD=AB即可.
故选D.
13.7 其中的任意三条组合有(4,4,4),(8,8,8),(10,10,10),(8,8,4),(8,8,10),(10,10,4),(10,10,8).故答案为7.
14.证明:∵AB=AC,
∴∠B=∠C.
∵DE⊥BC,
∴∠DEB=∠FEC=90°,
∴∠B+∠BDE=90°,∠C+∠F=90°,
∴∠BDE=∠F.
又∵∠ADF=∠BDE,
∴∠ADF=∠F,
∴AD=AF,
∴△ADF是等腰三角形.
15.解:(1)∵在△ABD中,AD=BD,
∴∠B=∠BAD.
∵∠ADC=∠B+∠BAD=80°,
∴∠B=∠ADC=40°.
(2)△ABC是等腰三角形.
理由:∵∠B=40°,∠BAC=70°,
∴∠C=18AC=70°,
∴∠C=∠BAC,
∴BA=BC,
∴△ABC是等腰三角形.
16.解:(1)证明:∵CD=CE,
∴∠E=∠CDE,
∴∠ACB=∠E+∠CDE=2∠E.
∵AD=DE,∴∠E=∠DAC.
∵AD平分∠BAC,
∴∠BAC=2∠DAC=2∠E,
∴∠ACB=∠BAC,∴AB=BC.
又∵AB=AC,∴AB=BC=AC,
∴△ABC是等边三角形.
(2)当AD为△ABC的BC边上的中线或高时,(1)中的结论仍然成立.
17.解:(1)当点Q到达点C时,PQ⊥AB.
理由:∵AB=AC=BC=6 cm,
∴当点Q到达点C时,t==3(s),
此时AP=3×1=3(cm),即P为AB的中点,
∴PQ⊥AB.
(2)能.当△BPQ为等边三角形时,BP=BQ,
∴6-t=2t,解得t=2.
∴当t=2时,△BPQ是等边三角形.
同课章节目录
