湘教版数学八年级上册同步课时练习:2.5 第2课时 全等三角形的判定1——SAS(含答案)
文档属性
| 名称 | 湘教版数学八年级上册同步课时练习:2.5 第2课时 全等三角形的判定1——SAS(含答案) | 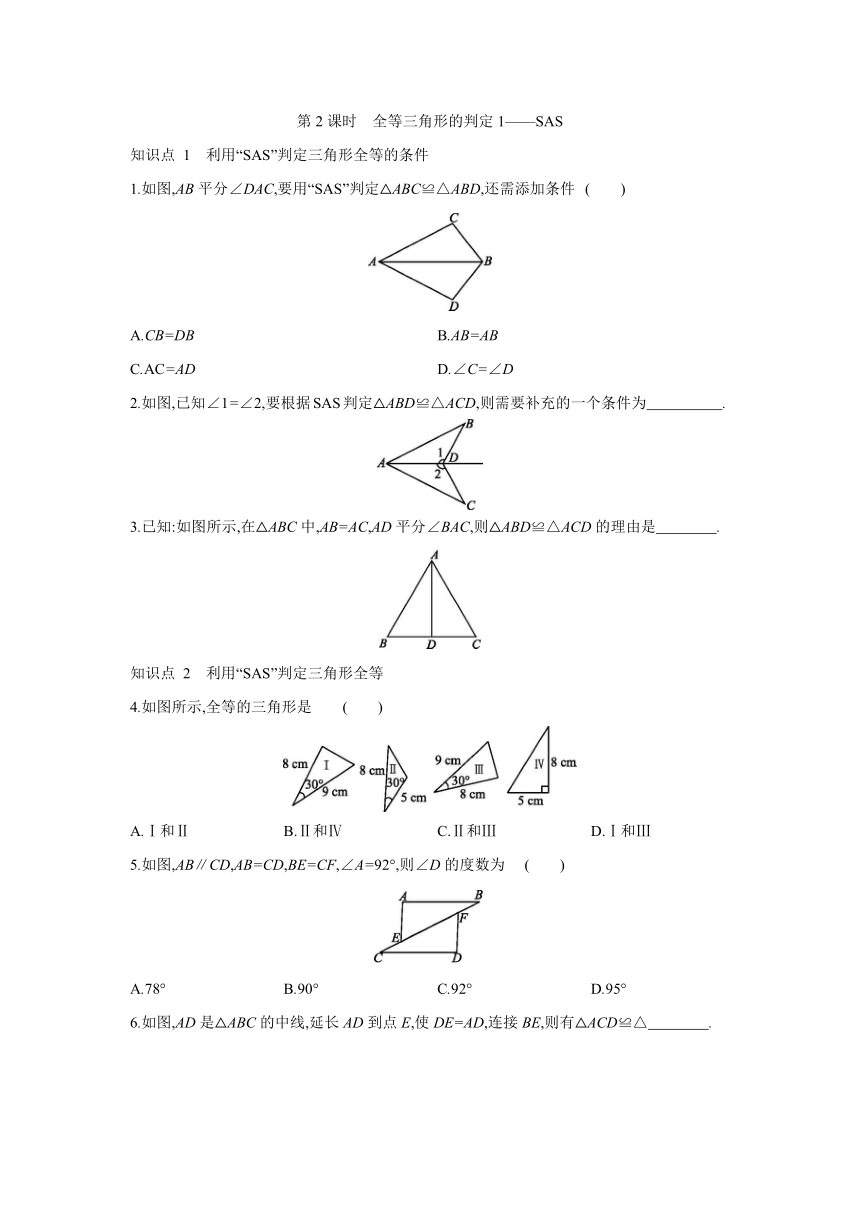 | |
| 格式 | docx | ||
| 文件大小 | 183.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-19 14:52:49 | ||
图片预览

文档简介
第2课时 全等三角形的判定1——SAS
知识点 1 利用“SAS”判定三角形全等的条件
1.如图,AB平分∠DAC,要用“SAS”判定△ABC≌△ABD,还需添加条件 ( )
A.CB=DB B.AB=AB
C.AC=AD D.∠C=∠D
2.如图,已知∠1=∠2,要根据SAS判定△ABD≌△ACD,则需要补充的一个条件为 .
3.已知:如图所示,在△ABC中,AB=AC,AD平分∠BAC,则△ABD≌△ACD的理由是 .
知识点 2 利用“SAS”判定三角形全等
4.如图所示,全等的三角形是 ( )
A.Ⅰ和Ⅱ B.Ⅱ和Ⅳ C.Ⅱ和Ⅲ D.Ⅰ和Ⅲ
5.如图,AB∥CD,AB=CD,BE=CF,∠A=92°,则∠D的度数为 ( )
A.78° B.90° C.92° D.95°
6.如图,AD是△ABC的中线,延长AD到点E,使DE=AD,连接BE,则有△ACD≌△ .
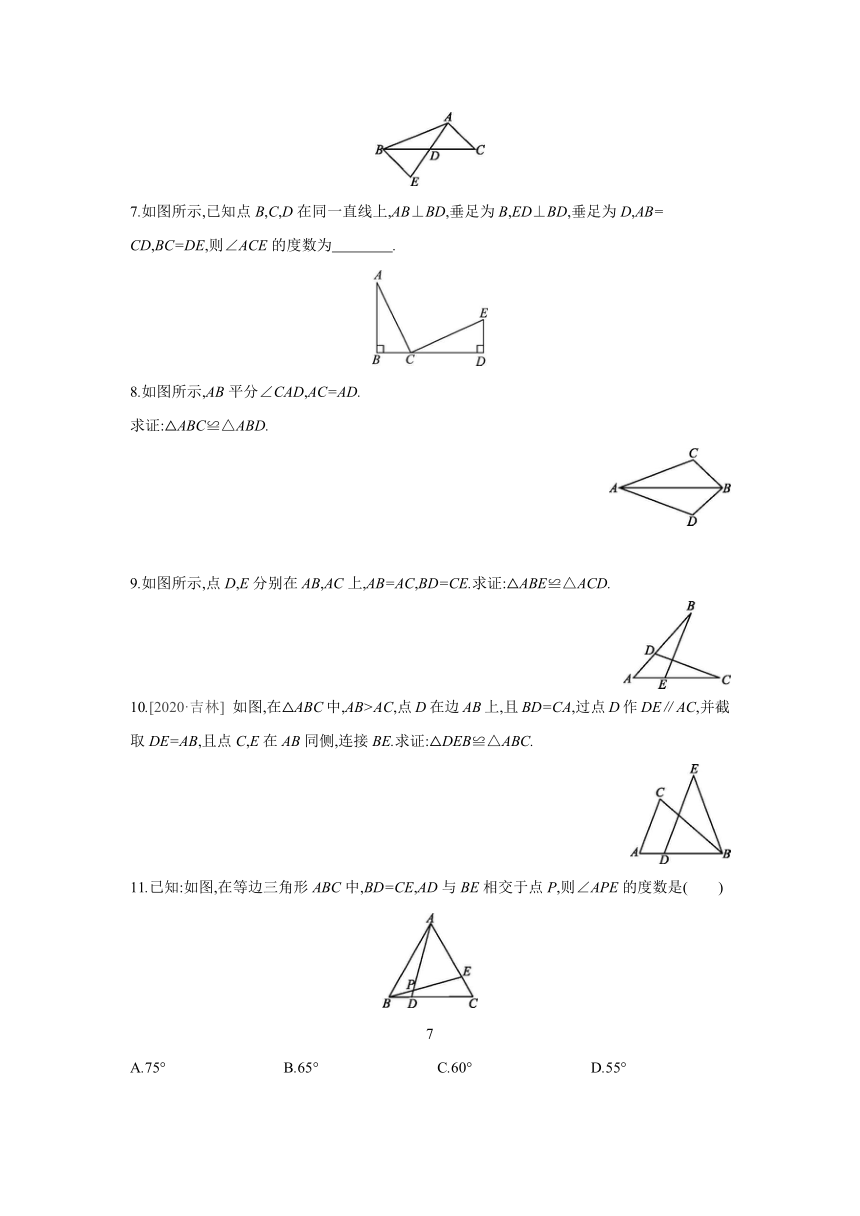
7.如图所示,已知点B,C,D在同一直线上,AB⊥BD,垂足为B,ED⊥BD,垂足为D,AB=
CD,BC=DE,则∠ACE的度数为 .
8.如图所示,AB平分∠CAD,AC=AD.
求证:△ABC≌△ABD.
9.如图所示,点D,E分别在AB,AC上,AB=AC,BD=CE.求证:△ABE≌△ACD.
10.[2020·吉林] 如图,在△ABC中,AB>AC,点D在边AB上,且BD=CA,过点D作DE∥AC,并截取DE=AB,且点C,E在AB同侧,连接BE.求证:△DEB≌△ABC.
11.已知:如图,在等边三角形ABC中,BD=CE,AD与BE相交于点P,则∠APE的度数是( )
7
A.75° B.65° C.60° D.55°
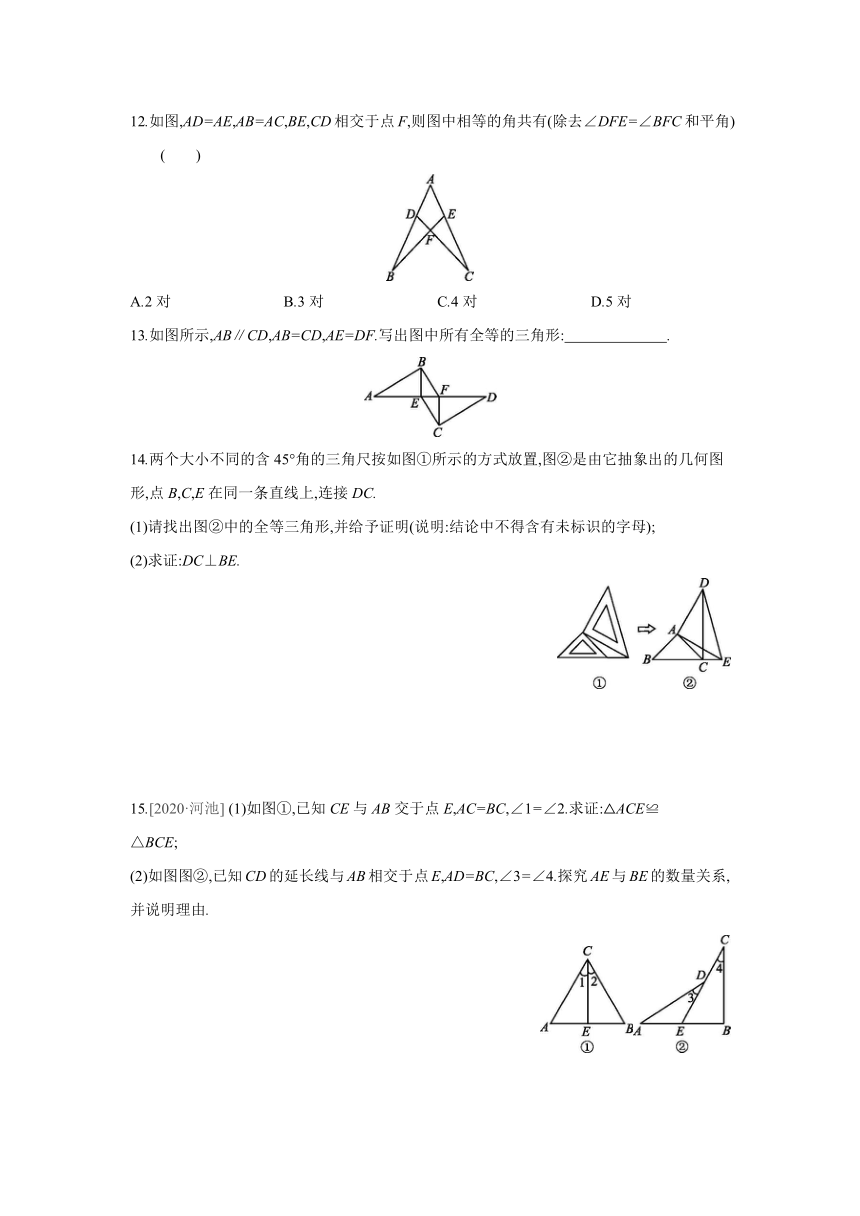
12.如图,AD=AE,AB=AC,BE,CD相交于点F,则图中相等的角共有(除去∠DFE=∠BFC和平角) ( )
A.2对 B.3对 C.4对 D.5对
13.如图所示,AB∥CD,AB=CD,AE=DF.写出图中所有全等的三角形: .
14.两个大小不同的含45°角的三角尺按如图①所示的方式放置,图②是由它抽象出的几何图形,点B,C,E在同一条直线上,连接DC.
(1)请找出图②中的全等三角形,并给予证明(说明:结论中不得含有未标识的字母);
(2)求证:DC⊥BE.
15.[2020·河池] (1)如图①,已知CE与AB交于点E,AC=BC,∠1=∠2.求证:△ACE≌
△BCE;
(2)如图图②,已知CD的延长线与AB相交于点E,AD=BC,∠3=∠4.探究AE与BE的数量关系,并说明理由.
16.如图所示,已知AE⊥AB,AF⊥AC,AE=AB,AF=AC,EC与BF交于点M.求证:
(1)EC=BF;
(2)EC⊥BF.
答案
1.C
2.BD=CD
3.SAS 已知AB=AC,∠BAD=∠CAD,AD=AD,即用SAS判定两个三角形全等.
4.D 夹30°角的两边中,Ⅰ,Ⅲ是对应相等的,根据SAS可知两个三角形全等.
5.C 根据SAS得△AEB≌△DFC,所以∠D=∠A=92°.
6.EBD
7.90° 由条件可证Rt△ABC≌Rt△CDE,∴∠A=∠DCE,∴∠DCE+∠ACB=∠A+
∠ACB=90°,故∠ACE=90°.
8.证明:∵AB平分∠CAD,
∴∠BAC=∠BAD.
在△ABC和△ABD中,
∴△ABC≌△ABD(SAS).
9.证明:∵AB=AC,BD=CE,
∴AB-BD=AC-CE,即AD=AE.
在△ABE和△ACD中,
∴△ABE≌△ACD(SAS).
10.证明:∵DE∥AC,∴∠EDB=∠A.
在△DEB与△ABC中,
∴△DEB≌△ABC(SAS).
11.C ∵△ABC是等边三角形,
∴∠ABD=∠C=60°,AB=BC.
又∵BD=CE,
∴△ABD≌△BCE,∴∠CBE=∠BAD,
∴∠APE=∠BAD+∠ABP=∠CBE+∠ABP=∠ABC=60°.
12.C ∵AB=AC,∠A=∠A,AE=AD,∴△ABE≌△ACD(SAS),
∴∠B=∠C,∠AEB=∠ADC,∴∠BEC=∠BDC.
又∵∠DFB=∠EFC,
∴共有4对角相等.故选C.
13.△ABE≌△DCF,△ABF≌△DCE,△BEF≌△CFE
14.解:(1)△ABE≌△ACD.
证明:∵△ABC与△AED均为等腰直角三角形,
∴AB=AC,AE=AD,∠BAC=∠EAD=90°,
∴∠BAC+∠CAE=∠EAD+∠CAE,
即∠BAE=∠CAD.
在△ABE和△ACD中,
∴△ABE≌△ACD(SAS).
(2)证明:由(1)知△ABE≌△ACD,
∴∠ACD=∠ABE=45°.
又∵∠ACB=45°,
∴∠BCD=∠ACB+∠ACD=90°,
∴DC⊥BE.
15.解:(1)证明:在△ACE和△BCE中,
∴△ACE≌△BCE(SAS).
(2)AE=BE.
理由:在CE上截取CF,使CF=DE,连接BF,如图图.
在△ADE和△BCF中,
∴△ADE≌△BCF(SAS),
∴AE=BF,∠AED=∠CFB.
又∵∠AED+∠BEF=180°,
∠CFB+∠EFB=180°,
∴∠BEF=∠EFB,
∴BE=BF,∴AE=BE.
16.证明:(1)∵AE⊥AB,AF⊥AC,
∴∠EAB=∠FAC=90°,
∴∠EAB+∠BAC=∠FAC+∠BAC,
即∠EAC=∠BAF.
在△EAC和△BAF中,
∴△EAC≌△BAF(SAS),
∴EC=BF.
(2)如图图,设AC与BF相交于点O.
∵△EAC≌△BAF,
∴∠AFO=∠OCM.
又∵∠AOF=∠MOC,
∴∠OMC=∠OAF=90°,
∴EC⊥BF.
知识点 1 利用“SAS”判定三角形全等的条件
1.如图,AB平分∠DAC,要用“SAS”判定△ABC≌△ABD,还需添加条件 ( )
A.CB=DB B.AB=AB
C.AC=AD D.∠C=∠D
2.如图,已知∠1=∠2,要根据SAS判定△ABD≌△ACD,则需要补充的一个条件为 .
3.已知:如图所示,在△ABC中,AB=AC,AD平分∠BAC,则△ABD≌△ACD的理由是 .
知识点 2 利用“SAS”判定三角形全等
4.如图所示,全等的三角形是 ( )
A.Ⅰ和Ⅱ B.Ⅱ和Ⅳ C.Ⅱ和Ⅲ D.Ⅰ和Ⅲ
5.如图,AB∥CD,AB=CD,BE=CF,∠A=92°,则∠D的度数为 ( )
A.78° B.90° C.92° D.95°
6.如图,AD是△ABC的中线,延长AD到点E,使DE=AD,连接BE,则有△ACD≌△ .
7.如图所示,已知点B,C,D在同一直线上,AB⊥BD,垂足为B,ED⊥BD,垂足为D,AB=
CD,BC=DE,则∠ACE的度数为 .
8.如图所示,AB平分∠CAD,AC=AD.
求证:△ABC≌△ABD.
9.如图所示,点D,E分别在AB,AC上,AB=AC,BD=CE.求证:△ABE≌△ACD.
10.[2020·吉林] 如图,在△ABC中,AB>AC,点D在边AB上,且BD=CA,过点D作DE∥AC,并截取DE=AB,且点C,E在AB同侧,连接BE.求证:△DEB≌△ABC.
11.已知:如图,在等边三角形ABC中,BD=CE,AD与BE相交于点P,则∠APE的度数是( )
7
A.75° B.65° C.60° D.55°
12.如图,AD=AE,AB=AC,BE,CD相交于点F,则图中相等的角共有(除去∠DFE=∠BFC和平角) ( )
A.2对 B.3对 C.4对 D.5对
13.如图所示,AB∥CD,AB=CD,AE=DF.写出图中所有全等的三角形: .
14.两个大小不同的含45°角的三角尺按如图①所示的方式放置,图②是由它抽象出的几何图形,点B,C,E在同一条直线上,连接DC.
(1)请找出图②中的全等三角形,并给予证明(说明:结论中不得含有未标识的字母);
(2)求证:DC⊥BE.
15.[2020·河池] (1)如图①,已知CE与AB交于点E,AC=BC,∠1=∠2.求证:△ACE≌
△BCE;
(2)如图图②,已知CD的延长线与AB相交于点E,AD=BC,∠3=∠4.探究AE与BE的数量关系,并说明理由.
16.如图所示,已知AE⊥AB,AF⊥AC,AE=AB,AF=AC,EC与BF交于点M.求证:
(1)EC=BF;
(2)EC⊥BF.
答案
1.C
2.BD=CD
3.SAS 已知AB=AC,∠BAD=∠CAD,AD=AD,即用SAS判定两个三角形全等.
4.D 夹30°角的两边中,Ⅰ,Ⅲ是对应相等的,根据SAS可知两个三角形全等.
5.C 根据SAS得△AEB≌△DFC,所以∠D=∠A=92°.
6.EBD
7.90° 由条件可证Rt△ABC≌Rt△CDE,∴∠A=∠DCE,∴∠DCE+∠ACB=∠A+
∠ACB=90°,故∠ACE=90°.
8.证明:∵AB平分∠CAD,
∴∠BAC=∠BAD.
在△ABC和△ABD中,
∴△ABC≌△ABD(SAS).
9.证明:∵AB=AC,BD=CE,
∴AB-BD=AC-CE,即AD=AE.
在△ABE和△ACD中,
∴△ABE≌△ACD(SAS).
10.证明:∵DE∥AC,∴∠EDB=∠A.
在△DEB与△ABC中,
∴△DEB≌△ABC(SAS).
11.C ∵△ABC是等边三角形,
∴∠ABD=∠C=60°,AB=BC.
又∵BD=CE,
∴△ABD≌△BCE,∴∠CBE=∠BAD,
∴∠APE=∠BAD+∠ABP=∠CBE+∠ABP=∠ABC=60°.
12.C ∵AB=AC,∠A=∠A,AE=AD,∴△ABE≌△ACD(SAS),
∴∠B=∠C,∠AEB=∠ADC,∴∠BEC=∠BDC.
又∵∠DFB=∠EFC,
∴共有4对角相等.故选C.
13.△ABE≌△DCF,△ABF≌△DCE,△BEF≌△CFE
14.解:(1)△ABE≌△ACD.
证明:∵△ABC与△AED均为等腰直角三角形,
∴AB=AC,AE=AD,∠BAC=∠EAD=90°,
∴∠BAC+∠CAE=∠EAD+∠CAE,
即∠BAE=∠CAD.
在△ABE和△ACD中,
∴△ABE≌△ACD(SAS).
(2)证明:由(1)知△ABE≌△ACD,
∴∠ACD=∠ABE=45°.
又∵∠ACB=45°,
∴∠BCD=∠ACB+∠ACD=90°,
∴DC⊥BE.
15.解:(1)证明:在△ACE和△BCE中,
∴△ACE≌△BCE(SAS).
(2)AE=BE.
理由:在CE上截取CF,使CF=DE,连接BF,如图图.
在△ADE和△BCF中,
∴△ADE≌△BCF(SAS),
∴AE=BF,∠AED=∠CFB.
又∵∠AED+∠BEF=180°,
∠CFB+∠EFB=180°,
∴∠BEF=∠EFB,
∴BE=BF,∴AE=BE.
16.证明:(1)∵AE⊥AB,AF⊥AC,
∴∠EAB=∠FAC=90°,
∴∠EAB+∠BAC=∠FAC+∠BAC,
即∠EAC=∠BAF.
在△EAC和△BAF中,
∴△EAC≌△BAF(SAS),
∴EC=BF.
(2)如图图,设AC与BF相交于点O.
∵△EAC≌△BAF,
∴∠AFO=∠OCM.
又∵∠AOF=∠MOC,
∴∠OMC=∠OAF=90°,
∴EC⊥BF.
同课章节目录
