湘教版数学八年级上册同步课时练习:2.5 第3课时 全等三角形的判定2——ASA(含答案)
文档属性
| 名称 | 湘教版数学八年级上册同步课时练习:2.5 第3课时 全等三角形的判定2——ASA(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 147.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-19 14:54:01 | ||
图片预览


文档简介
第3课时 全等三角形的判定2——ASA
知识点 1 利用“ASA”判定三角形全等的条件
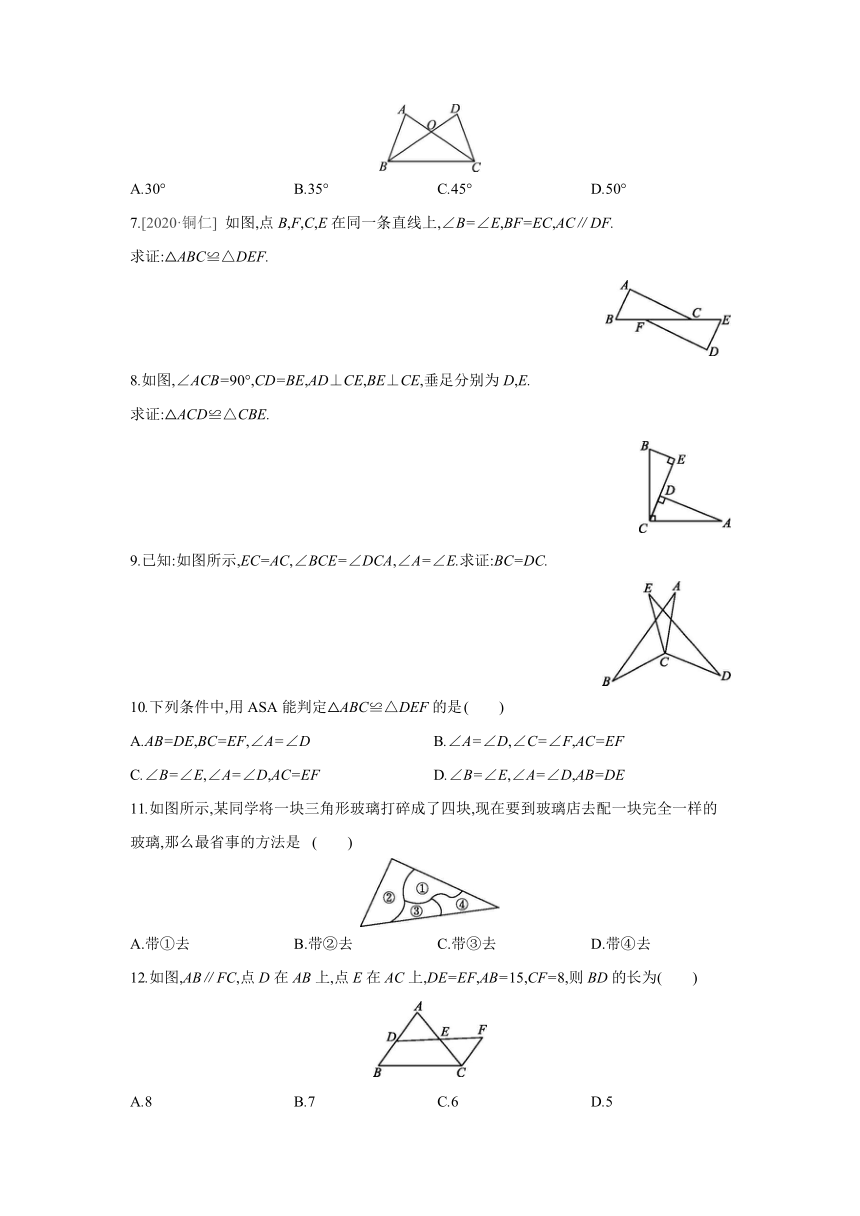
1.如图,已知点A,D,C,F在同一条直线上,∠A=∠EDF,AC=DF,要用“ASA”判定△ABC≌△DEF,还需要添加一个条件是 ( )
A.∠BCA=∠F B.AB=DE
C.BC=EF D.AB∥DE
2.如图,∠ADB=∠CDB,∠ABD=∠CBD,则判定△ABD≌△CBD的依据是 .
3.如图所示,AB与CD相交于点O,∠A=∠B,AO=BO,又因为 = ,
所以△AOC≌△BOD,其依据是 .
4.如图所示,已知点B,C,F,E在同一直线上,∠1=∠2,BC=EF,用ASA判定△ABC≌
△DEF,还需添加一个条件,这个条件可以是 (只需写出一个).
知识点 2 利用“ASA”判定三角形全等
5.如图,∠ADB=∠AEC,∠1=∠2,BD=CE,则有△ABD≌△ .
6.如图, ∠A=∠D,OA=OD,∠DCO=35°, 则∠ABO的度数为 ( )
A.30° B.35° C.45° D.50°
7.[2020·铜仁] 如图,点B,F,C,E在同一条直线上,∠B=∠E,BF=EC,AC∥DF.
求证:△ABC≌△DEF.
8.如图,∠ACB=90°,CD=BE,AD⊥CE,BE⊥CE,垂足分别为D,E.
求证:△ACD≌△CBE.
9.已知:如图所示,EC=AC,∠BCE=∠DCA,∠A=∠E.求证:BC=DC.
10.下列条件中,用ASA能判定△ABC≌△DEF的是 ( )
A.AB=DE,BC=EF,∠A=∠D B.∠A=∠D,∠C=∠F,AC=EF
C.∠B=∠E,∠A=∠D,AC=EF D.∠B=∠E,∠A=∠D,AB=DE
11.如图所示,某同学将一块三角形玻璃打碎成了四块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的方法是 ( )
A.带①去 B.带②去 C.带③去 D.带④去
12.如图,AB∥FC,点D在AB上,点E在AC上,DE=EF,AB=15,CF=8,则BD的长为( )
A.8 B.7 C.6 D.5
13.如图,已知AE∥BD,点B,C,D在同一直线上.若要用“角边角”判定△AEC≌△DCE,则需添加的一组平行线是 .
14.如图,在Rt△ABC中,∠ABC=90°,点D在BC的延长线上,且BD=AB,过点B作BE⊥AC,与BD的垂线DE交于点E.
求证:△ABC≌△BDE.
15.已知△ABN和△ACM的位置如图所示,AB=AC,AD=AE,∠1=∠2.
求证:(1)BD=CE;
(2)∠M=∠N.
16.如图所示,已知△ABC为等边三角形,QR⊥AB,垂足为R,PQ⊥AC,垂足为Q,RP⊥BC,垂足为P,且AR=BP=CQ.
求证:△RPQ为等边三角形.
7
答案
1.A
2.ASA
3.∠AOC ∠BOD ASA
4.∠B=∠E(答案不唯一)
5.ACE
6.B
7.证明:∵AC∥DF,∴∠ACB=∠DFE.
∵BF=CE,
∴BF+CF=CE+CF,
即BC=EF.
在△ABC和△DEF中,
∴△ABC≌△DEF(ASA).
8.证明:∵AD⊥CE,BE⊥CE,
∴∠ADC=∠E=90°,
∴∠B+∠BCE=90°.
∵∠ACB=90°,
∴∠BCE+∠ACD=90°,
∴∠B=∠ACD.
在△ACD和△CBE中,
∴△ACD≌△CBE(ASA).
9.证明:∵∠BCE=∠DCA,
∴∠BCE+∠ACE=∠DCA+∠ACE,
即∠BCA=∠DCE.
在△BCA和△DCE中,
∴△BCA≌△DCE(ASA),∴BC=DC.
10.D
11.B 此题要抓住问题的本质:要证两个三角形全等需要确定三角形的哪几个元素.通过观察比较就会容易得出第②块碎玻璃可以确定三角形的两角及其夹边.故选B.
12.B
13.AC∥DE ∵AE∥BD,
∴∠AEC=∠DCE.
又∵CE=EC,
∴当∠ACE=∠DEC时,△AEC≌△DCE(ASA),此时有AC∥DE.
14.证明:∵∠ABC=90°,
∴∠ABE+∠DBE=90°.
∵BE⊥AC,
∴∠ABE+∠A=90°,
∴∠A=∠DBE.
∵DE是BD的垂线,
∴∠D=90°.
在△ABC和△BDE中,
∴△ABC≌△BDE(ASA).
15.证明:(1)在△ABD和△ACE中,
∴△ABD≌△ACE(SAS),
∴BD=CE.
(2)∵∠1=∠2,
∴∠1+∠DAE=∠2+∠DAE,
即∠BAN=∠CAM.
由(1)得△ABD≌△ACE,
∴∠B=∠C.
在△ACM和△ABN中,
∴△ACM≌△ABN(ASA),∴∠M=∠N.
16.证明:∵△ABC为等边三角形,
∴∠A=∠B=∠C=60°.
又∵QR⊥AB,RP⊥BC,PQ⊥AC,
∴∠ARQ=∠BPR=∠CQP=90°.
在△ARQ和△BPR中,
∴△ARQ≌△BPR(ASA),
∴RQ=PR.
同理可证△BPR≌△CQP,
∴PR=QP,
∴RQ=PR=QP,
∴△RPQ为等边三角形.
知识点 1 利用“ASA”判定三角形全等的条件
1.如图,已知点A,D,C,F在同一条直线上,∠A=∠EDF,AC=DF,要用“ASA”判定△ABC≌△DEF,还需要添加一个条件是 ( )
A.∠BCA=∠F B.AB=DE
C.BC=EF D.AB∥DE
2.如图,∠ADB=∠CDB,∠ABD=∠CBD,则判定△ABD≌△CBD的依据是 .
3.如图所示,AB与CD相交于点O,∠A=∠B,AO=BO,又因为 = ,
所以△AOC≌△BOD,其依据是 .
4.如图所示,已知点B,C,F,E在同一直线上,∠1=∠2,BC=EF,用ASA判定△ABC≌
△DEF,还需添加一个条件,这个条件可以是 (只需写出一个).
知识点 2 利用“ASA”判定三角形全等
5.如图,∠ADB=∠AEC,∠1=∠2,BD=CE,则有△ABD≌△ .
6.如图, ∠A=∠D,OA=OD,∠DCO=35°, 则∠ABO的度数为 ( )
A.30° B.35° C.45° D.50°
7.[2020·铜仁] 如图,点B,F,C,E在同一条直线上,∠B=∠E,BF=EC,AC∥DF.
求证:△ABC≌△DEF.
8.如图,∠ACB=90°,CD=BE,AD⊥CE,BE⊥CE,垂足分别为D,E.
求证:△ACD≌△CBE.
9.已知:如图所示,EC=AC,∠BCE=∠DCA,∠A=∠E.求证:BC=DC.
10.下列条件中,用ASA能判定△ABC≌△DEF的是 ( )
A.AB=DE,BC=EF,∠A=∠D B.∠A=∠D,∠C=∠F,AC=EF
C.∠B=∠E,∠A=∠D,AC=EF D.∠B=∠E,∠A=∠D,AB=DE
11.如图所示,某同学将一块三角形玻璃打碎成了四块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的方法是 ( )
A.带①去 B.带②去 C.带③去 D.带④去
12.如图,AB∥FC,点D在AB上,点E在AC上,DE=EF,AB=15,CF=8,则BD的长为( )
A.8 B.7 C.6 D.5
13.如图,已知AE∥BD,点B,C,D在同一直线上.若要用“角边角”判定△AEC≌△DCE,则需添加的一组平行线是 .
14.如图,在Rt△ABC中,∠ABC=90°,点D在BC的延长线上,且BD=AB,过点B作BE⊥AC,与BD的垂线DE交于点E.
求证:△ABC≌△BDE.
15.已知△ABN和△ACM的位置如图所示,AB=AC,AD=AE,∠1=∠2.
求证:(1)BD=CE;
(2)∠M=∠N.
16.如图所示,已知△ABC为等边三角形,QR⊥AB,垂足为R,PQ⊥AC,垂足为Q,RP⊥BC,垂足为P,且AR=BP=CQ.
求证:△RPQ为等边三角形.
7
答案
1.A
2.ASA
3.∠AOC ∠BOD ASA
4.∠B=∠E(答案不唯一)
5.ACE
6.B
7.证明:∵AC∥DF,∴∠ACB=∠DFE.
∵BF=CE,
∴BF+CF=CE+CF,
即BC=EF.
在△ABC和△DEF中,
∴△ABC≌△DEF(ASA).
8.证明:∵AD⊥CE,BE⊥CE,
∴∠ADC=∠E=90°,
∴∠B+∠BCE=90°.
∵∠ACB=90°,
∴∠BCE+∠ACD=90°,
∴∠B=∠ACD.
在△ACD和△CBE中,
∴△ACD≌△CBE(ASA).
9.证明:∵∠BCE=∠DCA,
∴∠BCE+∠ACE=∠DCA+∠ACE,
即∠BCA=∠DCE.
在△BCA和△DCE中,
∴△BCA≌△DCE(ASA),∴BC=DC.
10.D
11.B 此题要抓住问题的本质:要证两个三角形全等需要确定三角形的哪几个元素.通过观察比较就会容易得出第②块碎玻璃可以确定三角形的两角及其夹边.故选B.
12.B
13.AC∥DE ∵AE∥BD,
∴∠AEC=∠DCE.
又∵CE=EC,
∴当∠ACE=∠DEC时,△AEC≌△DCE(ASA),此时有AC∥DE.
14.证明:∵∠ABC=90°,
∴∠ABE+∠DBE=90°.
∵BE⊥AC,
∴∠ABE+∠A=90°,
∴∠A=∠DBE.
∵DE是BD的垂线,
∴∠D=90°.
在△ABC和△BDE中,
∴△ABC≌△BDE(ASA).
15.证明:(1)在△ABD和△ACE中,
∴△ABD≌△ACE(SAS),
∴BD=CE.
(2)∵∠1=∠2,
∴∠1+∠DAE=∠2+∠DAE,
即∠BAN=∠CAM.
由(1)得△ABD≌△ACE,
∴∠B=∠C.
在△ACM和△ABN中,
∴△ACM≌△ABN(ASA),∴∠M=∠N.
16.证明:∵△ABC为等边三角形,
∴∠A=∠B=∠C=60°.
又∵QR⊥AB,RP⊥BC,PQ⊥AC,
∴∠ARQ=∠BPR=∠CQP=90°.
在△ARQ和△BPR中,
∴△ARQ≌△BPR(ASA),
∴RQ=PR.
同理可证△BPR≌△CQP,
∴PR=QP,
∴RQ=PR=QP,
∴△RPQ为等边三角形.
同课章节目录
