湘教版数学八年级上册同步课时练习:2.5 第5课时 全等三角形的判定4——SSS(含答案)
文档属性
| 名称 | 湘教版数学八年级上册同步课时练习:2.5 第5课时 全等三角形的判定4——SSS(含答案) | 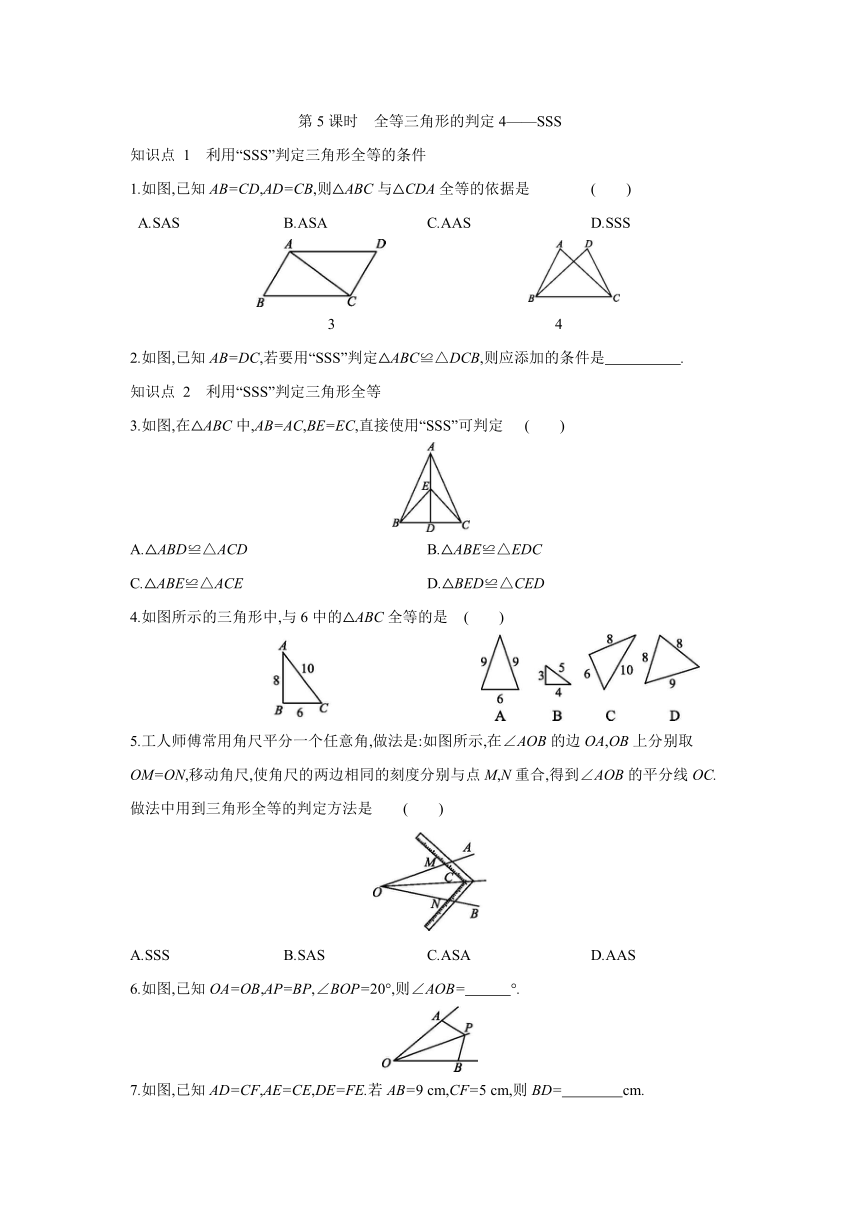 | |
| 格式 | docx | ||
| 文件大小 | 160.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-19 15:01:31 | ||
图片预览

文档简介
第5课时 全等三角形的判定4——SSS
知识点 1 利用“SSS”判定三角形全等的条件
1.如图,已知AB=CD,AD=CB,则△ABC与△CDA全等的依据是 ( )
A.SAS B.ASA C.AAS D.SSS
3 4
2.如图,已知AB=DC,若要用“SSS”判定△ABC≌△DCB,则应添加的条件是 .
知识点 2 利用“SSS”判定三角形全等
3.如图,在△ABC中,AB=AC,BE=EC,直接使用“SSS”可判定 ( )
A.△ABD≌△ACD B.△ABE≌△EDC
C.△ABE≌△ACE D.△BED≌△CED
4.如图所示的三角形中,与6中的△ABC全等的是 ( )
5.工人师傅常用角尺平分一个任意角,做法是:如图所示,在∠AOB的边OA,OB上分别取OM=ON,移动角尺,使角尺的两边相同的刻度分别与点M,N重合,得到∠AOB的平分线OC.做法中用到三角形全等的判定方法是 ( )
A.SSS B.SAS C.ASA D.AAS
6.如图,已知OA=OB,AP=BP,∠BOP=20°,则∠AOB= °.
7.如图,已知AD=CF,AE=CE,DE=FE.若AB=9 cm,CF=5 cm,则BD= cm.
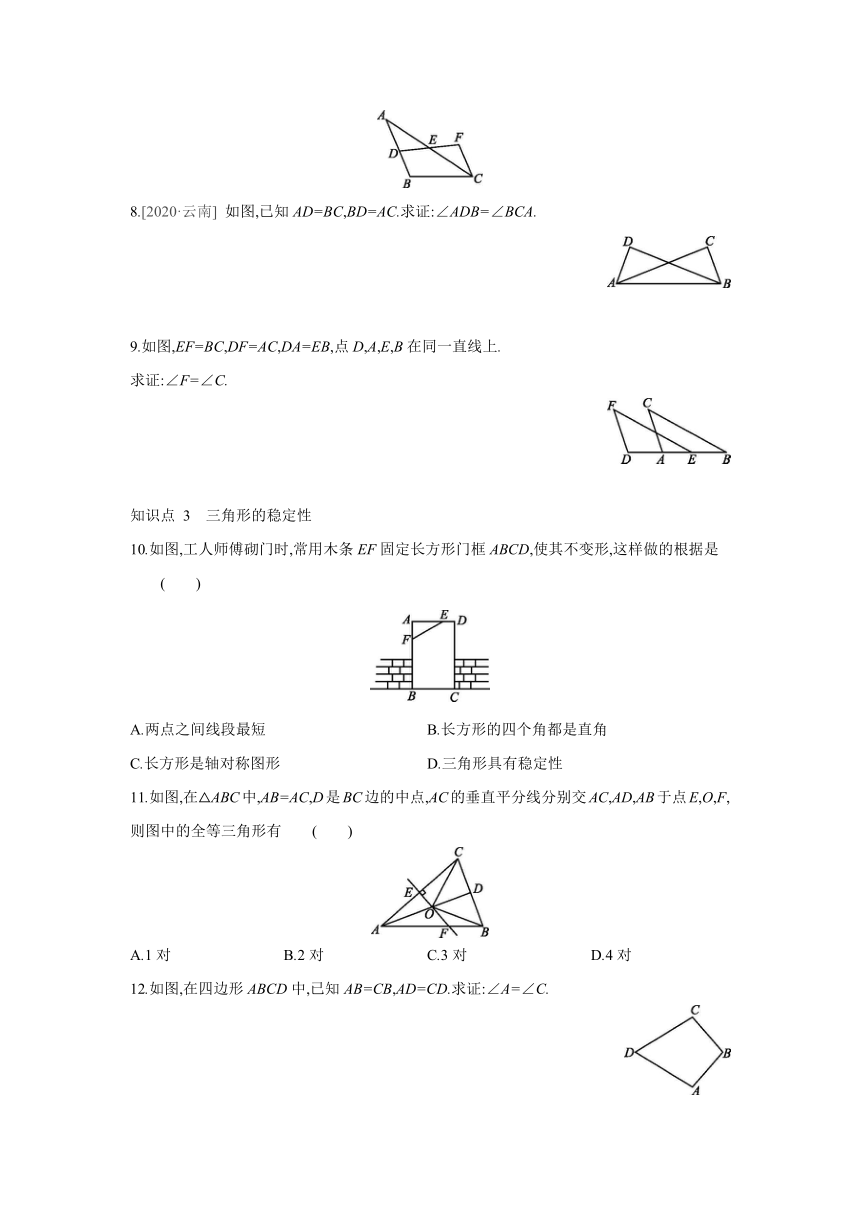
8.[2020·云南] 如图,已知AD=BC,BD=AC.求证:∠ADB=∠BCA.
9.如图,EF=BC,DF=AC,DA=EB,点D,A,E,B在同一直线上.
求证:∠F=∠C.
知识点 3 三角形的稳定性
10.如图,工人师傅砌门时,常用木条EF固定长方形门框ABCD,使其不变形,这样做的根据是 ( )
A.两点之间线段最短 B.长方形的四个角都是直角
C.长方形是轴对称图形 D.三角形具有稳定性
11.如图,在△ABC中,AB=AC,D是BC边的中点,AC的垂直平分线分别交AC,AD,AB于点E,O,F,则图中的全等三角形有 ( )
A.1对 B.2对 C.3对 D.4对
12.如图,在四边形ABCD中,已知AB=CB,AD=CD.求证:∠A=∠C.
13.如图,已知AB=AC,AD=AE,BD=CE.求证:∠3=∠1+∠2.
14.如图,AB=AC,DB=DC,EB=EC.
(1)图中有几对全等三角形 请一一写出来;
(2)选择(1)中的一对全等三角形加以证明.
15.如图,在△ABC和△DCB中,AB=DC,AC=DB,AC与DB相交于点M.
(1)求证:△AMB≌△DMC;
(2)过点C作CN∥BD,过点B作BN∥AC,CN与BN相交于点N,试判断线段BN与CN的数量关系,并证明你的结论.
答案
1.D 在△ABC和△CDA中,∴△ABC≌△CDA.
2.AC=DB
3.C 4.C
5.A 已知两个三角形的三边分别相等,由SSS可得△OMC≌△ONC,从而有∠MOC=∠NOC,所以OC是∠AOB的平分线.故选A.
6.40 7.4
8.证明:在△ADB和△BCA中,
∴△ADB≌△BCA(SSS),
∴∠ADB=∠BCA.
9.证明:∵DA=BE,
∴DA+AE=BE+AE,即DE=AB.
在△DEF和△ABC中,
∴△DEF≌△ABC(SSS),
∴∠F=∠C.
10.D
11.D 根据SSS得到△ABD≌△ACD,△AOE≌△COE,△BOD≌△COD,△AOC≌△AOB,共4对.
12.证明:如图图,连接BD.
在△ABD与△CBD中,
∴△ABD≌△CBD(SSS),
∴∠A=∠C.
13.证明:在△ABD和△ACE中,
∴△ABD≌△ACE(SSS),
∴∠BAD=∠1,∠ABD=∠2.
∵∠3=∠BAD+∠ABD,
∴∠3=∠1+∠2.
14.解:(1)3对,分别为△ABD≌△ACD,△ABE≌△ACE,△DBE≌△DCE.
(2)(答案不唯一)以△ABD≌△ACD为例:
证明:在△ABD和△ACD中,
∴△ABD≌△ACD(SSS).
15.解:(1)证明:在△ABC和△DCB中,
∴△ABC≌△DCB(SSS),∴∠A=∠D.
在△AMB和△DMC中,
∴△AMB≌△DMC(AAS).
(2)BN=CN.
证明:∵CN∥BD,BN∥AC,
∴∠MBC=∠BCN,∠MCB=∠CBN.
由(1)知△ABC≌△DCB,
∴∠MBC=∠MCB,
∴∠BCN=∠CBN,
∴BN=CN.
知识点 1 利用“SSS”判定三角形全等的条件
1.如图,已知AB=CD,AD=CB,则△ABC与△CDA全等的依据是 ( )
A.SAS B.ASA C.AAS D.SSS
3 4
2.如图,已知AB=DC,若要用“SSS”判定△ABC≌△DCB,则应添加的条件是 .
知识点 2 利用“SSS”判定三角形全等
3.如图,在△ABC中,AB=AC,BE=EC,直接使用“SSS”可判定 ( )
A.△ABD≌△ACD B.△ABE≌△EDC
C.△ABE≌△ACE D.△BED≌△CED
4.如图所示的三角形中,与6中的△ABC全等的是 ( )
5.工人师傅常用角尺平分一个任意角,做法是:如图所示,在∠AOB的边OA,OB上分别取OM=ON,移动角尺,使角尺的两边相同的刻度分别与点M,N重合,得到∠AOB的平分线OC.做法中用到三角形全等的判定方法是 ( )
A.SSS B.SAS C.ASA D.AAS
6.如图,已知OA=OB,AP=BP,∠BOP=20°,则∠AOB= °.
7.如图,已知AD=CF,AE=CE,DE=FE.若AB=9 cm,CF=5 cm,则BD= cm.
8.[2020·云南] 如图,已知AD=BC,BD=AC.求证:∠ADB=∠BCA.
9.如图,EF=BC,DF=AC,DA=EB,点D,A,E,B在同一直线上.
求证:∠F=∠C.
知识点 3 三角形的稳定性
10.如图,工人师傅砌门时,常用木条EF固定长方形门框ABCD,使其不变形,这样做的根据是 ( )
A.两点之间线段最短 B.长方形的四个角都是直角
C.长方形是轴对称图形 D.三角形具有稳定性
11.如图,在△ABC中,AB=AC,D是BC边的中点,AC的垂直平分线分别交AC,AD,AB于点E,O,F,则图中的全等三角形有 ( )
A.1对 B.2对 C.3对 D.4对
12.如图,在四边形ABCD中,已知AB=CB,AD=CD.求证:∠A=∠C.
13.如图,已知AB=AC,AD=AE,BD=CE.求证:∠3=∠1+∠2.
14.如图,AB=AC,DB=DC,EB=EC.
(1)图中有几对全等三角形 请一一写出来;
(2)选择(1)中的一对全等三角形加以证明.
15.如图,在△ABC和△DCB中,AB=DC,AC=DB,AC与DB相交于点M.
(1)求证:△AMB≌△DMC;
(2)过点C作CN∥BD,过点B作BN∥AC,CN与BN相交于点N,试判断线段BN与CN的数量关系,并证明你的结论.
答案
1.D 在△ABC和△CDA中,∴△ABC≌△CDA.
2.AC=DB
3.C 4.C
5.A 已知两个三角形的三边分别相等,由SSS可得△OMC≌△ONC,从而有∠MOC=∠NOC,所以OC是∠AOB的平分线.故选A.
6.40 7.4
8.证明:在△ADB和△BCA中,
∴△ADB≌△BCA(SSS),
∴∠ADB=∠BCA.
9.证明:∵DA=BE,
∴DA+AE=BE+AE,即DE=AB.
在△DEF和△ABC中,
∴△DEF≌△ABC(SSS),
∴∠F=∠C.
10.D
11.D 根据SSS得到△ABD≌△ACD,△AOE≌△COE,△BOD≌△COD,△AOC≌△AOB,共4对.
12.证明:如图图,连接BD.
在△ABD与△CBD中,
∴△ABD≌△CBD(SSS),
∴∠A=∠C.
13.证明:在△ABD和△ACE中,
∴△ABD≌△ACE(SSS),
∴∠BAD=∠1,∠ABD=∠2.
∵∠3=∠BAD+∠ABD,
∴∠3=∠1+∠2.
14.解:(1)3对,分别为△ABD≌△ACD,△ABE≌△ACE,△DBE≌△DCE.
(2)(答案不唯一)以△ABD≌△ACD为例:
证明:在△ABD和△ACD中,
∴△ABD≌△ACD(SSS).
15.解:(1)证明:在△ABC和△DCB中,
∴△ABC≌△DCB(SSS),∴∠A=∠D.
在△AMB和△DMC中,
∴△AMB≌△DMC(AAS).
(2)BN=CN.
证明:∵CN∥BD,BN∥AC,
∴∠MBC=∠BCN,∠MCB=∠CBN.
由(1)知△ABC≌△DCB,
∴∠MBC=∠MCB,
∴∠BCN=∠CBN,
∴BN=CN.
同课章节目录
