湘教版数学八年级上册同步课时练习:2.5 第6课时 全等三角形判定方法的综合应用(含答案)
文档属性
| 名称 | 湘教版数学八年级上册同步课时练习:2.5 第6课时 全等三角形判定方法的综合应用(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 167.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-19 15:05:22 | ||
图片预览



文档简介
第6课时 全等三角形判定方法的综合应用
知识点 1 判定三角形全等的条件
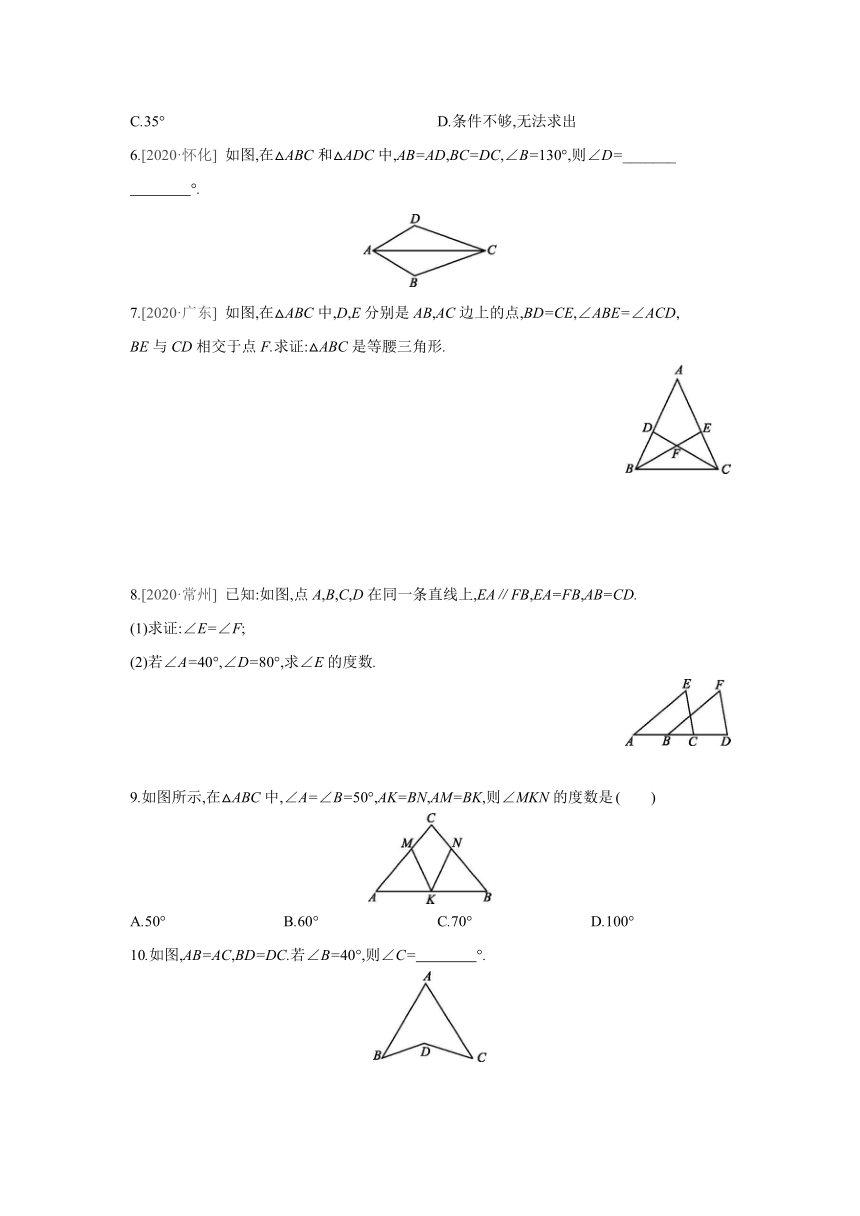
1.如图,已知点A,D,C,F在同一条直线上,AB=DE,∠B=∠E,添加一个条件仍无法证明△ABC≌△DEF的是 ( )
A.BC=EF B.BC∥EF
C.∠A=∠EDF D.AD=CF
2.如图,已知△ABD和△ACE均为等边三角形,那么△ADC≌△ABE的根据是 ( )
A.边边边 B.边角边 C.角边角 D.角角边
3.[2020·齐齐哈尔] 如图,已知在△ABD和△ABC中,∠DAB=∠CAB,点A,B,E在同一条直线上,若使△ABD≌△ABC,则还需添加的一个条件是 .(只填一个即可)
4.如图,已知∠CAE=∠DAB,AC=AD.给出下列条件:①AB=AE;②BC=ED;③∠C=∠D;④∠B=∠E.其中能判定△ABC≌△AED的条件为 .(注:把你认为正确的答案的序号都填上)
知识点 2 全等三角形判定与性质的综合
5.如图,OA=OB,OC=OD,∠D=35°,则∠C的度数为 ( )
3
A.60° B.50°
C.35° D.条件不够,无法求出
6.[2020·怀化] 如图,在△ABC和△ADC中,AB=AD,BC=DC,∠B=130°,则∠D=_______
°.
7.[2020·广东] 如图,在△ABC中,D,E分别是AB,AC边上的点,BD=CE,∠ABE=∠ACD,
BE与CD相交于点F.求证:△ABC是等腰三角形.
8.[2020·常州] 已知:如图,点A,B,C,D在同一条直线上,EA∥FB,EA=FB,AB=CD.
(1)求证:∠E=∠F;
(2)若∠A=40°,∠D=80°,求∠E的度数.
9.如图所示,在△ABC中,∠A=∠B=50°,AK=BN,AM=BK,则∠MKN的度数是 ( )
A.50° B.60° C.70° D.100°
10.如图,AB=AC,BD=DC.若∠B=40°,则∠C= °.
11.如图,点B,C,E在同一直线上,∠B=∠E=90°,AB=a,DE=b,AC=CD,∠D=60°,∠A=30°,则BE= (用含a,b的式子表示).
12.如图所示,在△ABC中,AC=BC,∠ACB=90°,AD平分∠CAB交BC于点D.求证:
AC+CD=AB.
13.[2020·烟台] 如图,在等边三角形ABC中,E是边AC上一定点,D是直线BC上一动点,以DE为一边作等边三角形DEF,连接CF.
【问题解决】
如图图①,若点D在边BC上,求证:CE+CF=CD;
【类比探究】
如图图②,若点D在边BC的延长线上,请探究线段CE,CF与CD之间存在怎样的数量关系,并说
明理由.
答案
1.D 若添加BC=EF.∵AB=DE,∠B=∠E,BC=EF,
∴△ABC≌△DEF(SAS);若添加BC∥EF,则∠ACB=∠F.
∵AB=DE,∠B=∠E,∠ACB=∠F,∴△ABC≌△DEF(AAS);
若添加∠A=∠EDF.∵∠A=∠EDF,AB=DE,∠B=∠E,∴△ABC≌△DEF(ASA);
若添加AD=CF,则无法证明△ABC≌△DEF.
2.B ∵△ABD和△ACE均为等边三角形,
∴∠DAB=∠CAE=60°,DA=BA,AC=AE,∴∠DAB+∠BAC=∠CAE+∠BAC,
即∠DAC=∠BAE,∴△ADC≌△ABE(SAS).
故选B.
3.答案不唯一,如图AD=AC或∠D=∠C或∠ABD=∠ABC等
∵∠DAB=∠CAB,AB=AB,
∴当添加AD=AC时,可根据“SAS”判定△ABD≌△ABC;
当添加∠D=∠C时,可根据“AAS”判定△ABD≌△ABC;
当添加∠ABD=∠ABC时,可根据“ASA”判定△ABD≌△ABC.
4.①③④ ∵∠CAE=∠DAB,
∴∠CAE+∠EAB=∠DAB+∠EAB,
即∠CAB=∠DAE.
又∵AC=AD,
∴要判定△ABC≌△AED,可添加的条件为:
①AB=AE(SAS);③∠C=∠D(ASA);④∠B=∠E(AAS).
故答案为①③④.
5.C 在△OAD和△OBC中,
∴△OAD≌△OBC(SAS),
∴∠C=∠D=35°.
故选C.
6.130 在△ADC和△ABC中,
∴△ADC≌△ABC(SSS),
∴∠D=∠B.
∵∠B=130°,
∴∠D=130°.
故答案为130.
7.证明:∵∠ABE=∠ACD,
∴∠DBF=∠ECF.
在△BDF和△CEF中,
∴△BDF≌△CEF(AAS),
∴BF=CF,
∴∠FBC=∠FCB,
∴∠DBF+∠FBC=∠ECF+∠FCB,
即∠ABC=∠ACB,
∴AB=AC,
∴△ABC是等腰三角形.
8.解:(1)证明:∵EA∥FB,
∴∠A=∠FBD.
∵AB=CD,
∴AB+BC=CD+BC,
即AC=BD.
在△EAC与△FBD中,
∴△EAC≌△FBD(SAS),
∴∠E=∠F.
(2)∵△EAC≌△FBD,
∴∠ECA=∠D=80°.
∵∠A=40°,
∴∠E=180°-40°-80°=60°.
9.A 在△AMK和△BKN中,
∴△AMK≌△BKN(SAS),
∴∠AMK=∠BKN.
∵∠A=∠B=50°,
∴∠AMK+∠AKM=130°,
∴∠BKN+∠AKM=130°,
∴∠MKN=50°.故选A.
10.40
11.a+b ∵∠E=90°,∠D=60°,
∴∠DCE=90°-60°=30°=∠A.
在△ABC和△CED中,
∴△ABC≌△CED(AAS),
∴BC=DE=b,CE=AB=a,
∴BE=BC+CE=a+b.
12.证明:如图图,过点D作DE⊥AB,垂足为E.
∵∠ACB=90°,
∴∠ACD=∠AED.
∵AD平分∠CAB,
∴∠CAD=∠EAD.
在△ACD和△AED中,
∴△ACD≌△AED(AAS),
∴AC=AE,CD=ED.
∵AC=BC,∠ACB=90°,
∴△ABC是等腰直角三角形,
∴∠B=∠CAB=45°,
∴∠BDE=180°-90°-45°=45°,
∴∠BDE=∠B,
∴CD=ED=EB,
∴AC+CD=AE+EB=AB.
13.解:【问题解决】证明:在CD上取点H,使CH=CE,连接EH,如图图①所示.
∵△ABC是等边三角形,
∴∠ECH=60°.
又∵CE=CH,
∴△CEH是等边三角形,
∴EH=CE=CH,∠CEH=60°.
∵△DEF是等边三角形,
∴DE=FE,∠DEF=60°,
∴∠DEF-∠HEF=∠CEH-∠HEF,
即∠DEH=∠FEC.
在△DEH和△FEC中,
∴△DEH≌△FEC(SAS),
∴DH=CF.
∵CH+DH=CD,
∴CE+CF=CD.
【类比探究】线段CE,CF与CD之间的数量关系是CF=CD+CE.理由如图下:
过点D作DG∥AB,交AC的延长线于点G,如图图②所示.
∵△ABC是等边三角形,
∴∠A=∠B=60°.
∵DG∥AB,
∴∠GDC=∠B=60°,∠DGC=∠A=60°,
∴∠GDC=∠DGC=60°,
∴∠DCG=60°,
∴△GCD为等边三角形,
∴GD=CD=CG.
∵△DEF为等边三角形,
∴ED=FD,∠EDF=60°=∠GDC,
∴∠EDF+∠CDE=∠GDC+∠CDE,
即∠FDC=∠EDG.
在△EGD和△FCD中,
∴△EGD≌△FCD(SAS),
∴EG=FC.
∵EG=CE+CG,∴CF=CE+CG=CD+CE.
知识点 1 判定三角形全等的条件
1.如图,已知点A,D,C,F在同一条直线上,AB=DE,∠B=∠E,添加一个条件仍无法证明△ABC≌△DEF的是 ( )
A.BC=EF B.BC∥EF
C.∠A=∠EDF D.AD=CF
2.如图,已知△ABD和△ACE均为等边三角形,那么△ADC≌△ABE的根据是 ( )
A.边边边 B.边角边 C.角边角 D.角角边
3.[2020·齐齐哈尔] 如图,已知在△ABD和△ABC中,∠DAB=∠CAB,点A,B,E在同一条直线上,若使△ABD≌△ABC,则还需添加的一个条件是 .(只填一个即可)
4.如图,已知∠CAE=∠DAB,AC=AD.给出下列条件:①AB=AE;②BC=ED;③∠C=∠D;④∠B=∠E.其中能判定△ABC≌△AED的条件为 .(注:把你认为正确的答案的序号都填上)
知识点 2 全等三角形判定与性质的综合
5.如图,OA=OB,OC=OD,∠D=35°,则∠C的度数为 ( )
3
A.60° B.50°
C.35° D.条件不够,无法求出
6.[2020·怀化] 如图,在△ABC和△ADC中,AB=AD,BC=DC,∠B=130°,则∠D=_______
°.
7.[2020·广东] 如图,在△ABC中,D,E分别是AB,AC边上的点,BD=CE,∠ABE=∠ACD,
BE与CD相交于点F.求证:△ABC是等腰三角形.
8.[2020·常州] 已知:如图,点A,B,C,D在同一条直线上,EA∥FB,EA=FB,AB=CD.
(1)求证:∠E=∠F;
(2)若∠A=40°,∠D=80°,求∠E的度数.
9.如图所示,在△ABC中,∠A=∠B=50°,AK=BN,AM=BK,则∠MKN的度数是 ( )
A.50° B.60° C.70° D.100°
10.如图,AB=AC,BD=DC.若∠B=40°,则∠C= °.
11.如图,点B,C,E在同一直线上,∠B=∠E=90°,AB=a,DE=b,AC=CD,∠D=60°,∠A=30°,则BE= (用含a,b的式子表示).
12.如图所示,在△ABC中,AC=BC,∠ACB=90°,AD平分∠CAB交BC于点D.求证:
AC+CD=AB.
13.[2020·烟台] 如图,在等边三角形ABC中,E是边AC上一定点,D是直线BC上一动点,以DE为一边作等边三角形DEF,连接CF.
【问题解决】
如图图①,若点D在边BC上,求证:CE+CF=CD;
【类比探究】
如图图②,若点D在边BC的延长线上,请探究线段CE,CF与CD之间存在怎样的数量关系,并说
明理由.
答案
1.D 若添加BC=EF.∵AB=DE,∠B=∠E,BC=EF,
∴△ABC≌△DEF(SAS);若添加BC∥EF,则∠ACB=∠F.
∵AB=DE,∠B=∠E,∠ACB=∠F,∴△ABC≌△DEF(AAS);
若添加∠A=∠EDF.∵∠A=∠EDF,AB=DE,∠B=∠E,∴△ABC≌△DEF(ASA);
若添加AD=CF,则无法证明△ABC≌△DEF.
2.B ∵△ABD和△ACE均为等边三角形,
∴∠DAB=∠CAE=60°,DA=BA,AC=AE,∴∠DAB+∠BAC=∠CAE+∠BAC,
即∠DAC=∠BAE,∴△ADC≌△ABE(SAS).
故选B.
3.答案不唯一,如图AD=AC或∠D=∠C或∠ABD=∠ABC等
∵∠DAB=∠CAB,AB=AB,
∴当添加AD=AC时,可根据“SAS”判定△ABD≌△ABC;
当添加∠D=∠C时,可根据“AAS”判定△ABD≌△ABC;
当添加∠ABD=∠ABC时,可根据“ASA”判定△ABD≌△ABC.
4.①③④ ∵∠CAE=∠DAB,
∴∠CAE+∠EAB=∠DAB+∠EAB,
即∠CAB=∠DAE.
又∵AC=AD,
∴要判定△ABC≌△AED,可添加的条件为:
①AB=AE(SAS);③∠C=∠D(ASA);④∠B=∠E(AAS).
故答案为①③④.
5.C 在△OAD和△OBC中,
∴△OAD≌△OBC(SAS),
∴∠C=∠D=35°.
故选C.
6.130 在△ADC和△ABC中,
∴△ADC≌△ABC(SSS),
∴∠D=∠B.
∵∠B=130°,
∴∠D=130°.
故答案为130.
7.证明:∵∠ABE=∠ACD,
∴∠DBF=∠ECF.
在△BDF和△CEF中,
∴△BDF≌△CEF(AAS),
∴BF=CF,
∴∠FBC=∠FCB,
∴∠DBF+∠FBC=∠ECF+∠FCB,
即∠ABC=∠ACB,
∴AB=AC,
∴△ABC是等腰三角形.
8.解:(1)证明:∵EA∥FB,
∴∠A=∠FBD.
∵AB=CD,
∴AB+BC=CD+BC,
即AC=BD.
在△EAC与△FBD中,
∴△EAC≌△FBD(SAS),
∴∠E=∠F.
(2)∵△EAC≌△FBD,
∴∠ECA=∠D=80°.
∵∠A=40°,
∴∠E=180°-40°-80°=60°.
9.A 在△AMK和△BKN中,
∴△AMK≌△BKN(SAS),
∴∠AMK=∠BKN.
∵∠A=∠B=50°,
∴∠AMK+∠AKM=130°,
∴∠BKN+∠AKM=130°,
∴∠MKN=50°.故选A.
10.40
11.a+b ∵∠E=90°,∠D=60°,
∴∠DCE=90°-60°=30°=∠A.
在△ABC和△CED中,
∴△ABC≌△CED(AAS),
∴BC=DE=b,CE=AB=a,
∴BE=BC+CE=a+b.
12.证明:如图图,过点D作DE⊥AB,垂足为E.
∵∠ACB=90°,
∴∠ACD=∠AED.
∵AD平分∠CAB,
∴∠CAD=∠EAD.
在△ACD和△AED中,
∴△ACD≌△AED(AAS),
∴AC=AE,CD=ED.
∵AC=BC,∠ACB=90°,
∴△ABC是等腰直角三角形,
∴∠B=∠CAB=45°,
∴∠BDE=180°-90°-45°=45°,
∴∠BDE=∠B,
∴CD=ED=EB,
∴AC+CD=AE+EB=AB.
13.解:【问题解决】证明:在CD上取点H,使CH=CE,连接EH,如图图①所示.
∵△ABC是等边三角形,
∴∠ECH=60°.
又∵CE=CH,
∴△CEH是等边三角形,
∴EH=CE=CH,∠CEH=60°.
∵△DEF是等边三角形,
∴DE=FE,∠DEF=60°,
∴∠DEF-∠HEF=∠CEH-∠HEF,
即∠DEH=∠FEC.
在△DEH和△FEC中,
∴△DEH≌△FEC(SAS),
∴DH=CF.
∵CH+DH=CD,
∴CE+CF=CD.
【类比探究】线段CE,CF与CD之间的数量关系是CF=CD+CE.理由如图下:
过点D作DG∥AB,交AC的延长线于点G,如图图②所示.
∵△ABC是等边三角形,
∴∠A=∠B=60°.
∵DG∥AB,
∴∠GDC=∠B=60°,∠DGC=∠A=60°,
∴∠GDC=∠DGC=60°,
∴∠DCG=60°,
∴△GCD为等边三角形,
∴GD=CD=CG.
∵△DEF为等边三角形,
∴ED=FD,∠EDF=60°=∠GDC,
∴∠EDF+∠CDE=∠GDC+∠CDE,
即∠FDC=∠EDG.
在△EGD和△FCD中,
∴△EGD≌△FCD(SAS),
∴EG=FC.
∵EG=CE+CG,∴CF=CE+CG=CD+CE.
同课章节目录
