沪科版数学七年级下册 6.1.1平方根 课件(共22张PPT)
文档属性
| 名称 | 沪科版数学七年级下册 6.1.1平方根 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-18 16:38:18 | ||
图片预览








文档简介
(共22张PPT)
此刻打盹,
你将做梦;
而此刻学习,你将圆梦。
This moment will nap, you will have a dream; But this moment study , you will interpret a dream.
寄语
6.1.1《平方根》沪科版
学习 目标
1
2
3
了解一个数的平方根和算术平方根的概念及符号表示;了解开方与乘方互为逆运算;理解平方根的性质。
会求一个非负数的平方根、算术平方根。
通过在学习中互相帮助、交流、合作,培养团队精神。
情境 导入
为了美化校园,学校打算建一个面积为225平方米的正方形植物园,这个正方形的边长应取多少?你能计算出来吗?
解:这个正方形的边长为x米,依题意有
因为
所以x=15,或x=-15
又x为非负数,所以x=15
答:这个正方形的边长为15米.
分析:正方形面积=边长的平方
( )2=225
如果一个数的平方等于a,那么这个数就叫做a的平方根(二次方根).
用数学语言表达即为:
若 ,则x叫做a的平方根.
平方根 概念
1、独立思考:?
(1)16的平方根是什么?
(2) 0的平方根是什么?
(3) -9有没有平方根?
2、请你编3道题目,同桌交换解答。
3、“交流”,你发现了什么
4、总结
探究交流
±4
0
没有
1
2
3
一个正数有两个平方根,它们互为相反数
零只有一个平方根,
0的平方根是0
负数没有平方根
平方根 性质
练一练
1.判断是非
(1)4是16的算术平方根;( )
(2) 是 的一个平方根;( )
(3) 的平方根是-5;( )
(4)0的算数平方根是0. ( )
√
√
×
√
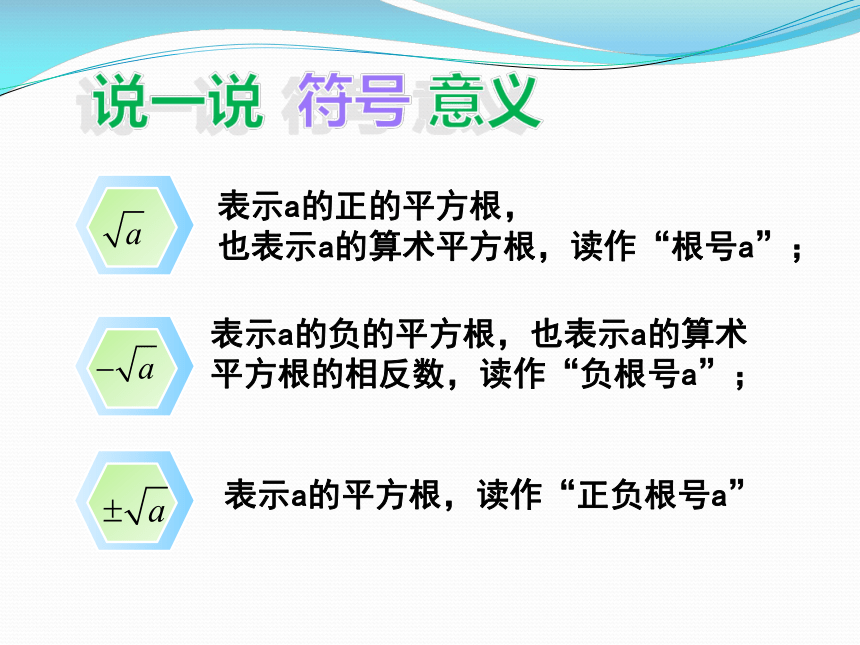
表示a的正的平方根,
也表示a的算术平方根,读作“根号a”;
表示a的负的平方根,也表示a的算术平方根的相反数,读作“负根号a”;
表示a的平方根,读作“正负根号a”
符号 意义
说一说
例1判断下列各数是否有平方根,为什么?
分析:正数和零有平方根,负数没有平方根
解:∵正数和零有平方根,负数没有平方根
∴ 有平方根, 没有平方根
二次根式有意义的条件:
被开方数是非负数(大于或等于0)
例题 精讲
2、下列各式是否有意义,说明理由:
二次根式有意义的条件:
被开方数是非负数(大于或等于0)
解:(1) ∵被开方数3>0, ∴ 有意义
(2) ∵被开方数-3<0, ∴ 无意义
(3) ∵被开方数9>0, ∴ 有意义
(4) ∵被开方数0, ∴ 有意义
练一练
例2求下列各数的平方根和算术平方根:
解:
∴1的平方根是±1 ,1的算术平方根是1
∴81的平方根是±9,81的算术平方根是9
即
即
例题 精讲
例2求下列各数的平方根和算术平方根:
解:
∴64的平方根是±8 ,64的算术平方根是8
∴ 的平方根是±3, 的算术平方根是3
即
即
例题 精讲
联系
区别
小结
非负数的平方根和算术平方根的联系与区别
1、二者有着包含关系:平方根中包含算术平方根,算术平方根是平方根中的非负的那一个
2、存在条件相同:非负数才有平方根和算术平方根
3、零的平方根和零的算术平方根都是零.
1、个数不同:一个正数有两个平方根,但只有一个算术平方根.
2、表示法不同:平方根表示为 ,而算术平方根表示为
3、求下列各数的平方根:
解:(1)∵
∴121的平方根是±11
即
(2)∵
∴ 的平方根是
即
练一练
平方与
开平方
互为逆运算
3、求下列各数的平方根:
解:(3)∵
∴0.0025的平方根是±0.05,
即
练一练
(4)∵
∴
的平方根是
即
方法
总结
求一个非负数的平方根,只要找出一个非负数,使得它的平方等于这个数,那么找出的那个非负数,连同它的相反数,就是所求的平方根
例3.说出下列各式的意义,并计算:
解:
表示 的算术平方根,
表示 的算术平方根,
例题 精讲
例3.说出下列各式表示的意义,并计算:
解:
表示 的负的平方根,
表示 的算术平方根,
例题 精讲
能力提升
1、已知2a-1和a+4是一个正数m的两个平方根,则a= ,m= .
分析:正数有两个平方根,并且互为相反数。
互为相反数两数和为0.
由2a-1+a+4=0得a的值,
代入得2a-1的值,
作2a-1的平方得m的值。
解:由2a-1+a+4=0得a=-1,
所以2a-1=-3
所以m=
能力提升
2、若 ,则abc= .
分析:几个非负数的和为零,则每个非负数都为零。
得a=-2,b=-5,c=4,得abc=40
解:由题得
所以a=-2,b=-5,c=4
所以abc=
概念及表示方法
A
B
式子有意义的条件
C
求非负数的(算术)平方根
E
非负性的运用
D
已知一个数的算术平方根,求原数
课堂总结
平方根
布置 作业
必做题习题6.1第1,2,5
选做题《同步学习》P2:7、8
此刻打盹,
你将做梦;
而此刻学习,你将圆梦。
This moment will nap, you will have a dream; But this moment study , you will interpret a dream.
寄语
6.1.1《平方根》沪科版
学习 目标
1
2
3
了解一个数的平方根和算术平方根的概念及符号表示;了解开方与乘方互为逆运算;理解平方根的性质。
会求一个非负数的平方根、算术平方根。
通过在学习中互相帮助、交流、合作,培养团队精神。
情境 导入
为了美化校园,学校打算建一个面积为225平方米的正方形植物园,这个正方形的边长应取多少?你能计算出来吗?
解:这个正方形的边长为x米,依题意有
因为
所以x=15,或x=-15
又x为非负数,所以x=15
答:这个正方形的边长为15米.
分析:正方形面积=边长的平方
( )2=225
如果一个数的平方等于a,那么这个数就叫做a的平方根(二次方根).
用数学语言表达即为:
若 ,则x叫做a的平方根.
平方根 概念
1、独立思考:?
(1)16的平方根是什么?
(2) 0的平方根是什么?
(3) -9有没有平方根?
2、请你编3道题目,同桌交换解答。
3、“交流”,你发现了什么
4、总结
探究交流
±4
0
没有
1
2
3
一个正数有两个平方根,它们互为相反数
零只有一个平方根,
0的平方根是0
负数没有平方根
平方根 性质
练一练
1.判断是非
(1)4是16的算术平方根;( )
(2) 是 的一个平方根;( )
(3) 的平方根是-5;( )
(4)0的算数平方根是0. ( )
√
√
×
√
表示a的正的平方根,
也表示a的算术平方根,读作“根号a”;
表示a的负的平方根,也表示a的算术平方根的相反数,读作“负根号a”;
表示a的平方根,读作“正负根号a”
符号 意义
说一说
例1判断下列各数是否有平方根,为什么?
分析:正数和零有平方根,负数没有平方根
解:∵正数和零有平方根,负数没有平方根
∴ 有平方根, 没有平方根
二次根式有意义的条件:
被开方数是非负数(大于或等于0)
例题 精讲
2、下列各式是否有意义,说明理由:
二次根式有意义的条件:
被开方数是非负数(大于或等于0)
解:(1) ∵被开方数3>0, ∴ 有意义
(2) ∵被开方数-3<0, ∴ 无意义
(3) ∵被开方数9>0, ∴ 有意义
(4) ∵被开方数0, ∴ 有意义
练一练
例2求下列各数的平方根和算术平方根:
解:
∴1的平方根是±1 ,1的算术平方根是1
∴81的平方根是±9,81的算术平方根是9
即
即
例题 精讲
例2求下列各数的平方根和算术平方根:
解:
∴64的平方根是±8 ,64的算术平方根是8
∴ 的平方根是±3, 的算术平方根是3
即
即
例题 精讲
联系
区别
小结
非负数的平方根和算术平方根的联系与区别
1、二者有着包含关系:平方根中包含算术平方根,算术平方根是平方根中的非负的那一个
2、存在条件相同:非负数才有平方根和算术平方根
3、零的平方根和零的算术平方根都是零.
1、个数不同:一个正数有两个平方根,但只有一个算术平方根.
2、表示法不同:平方根表示为 ,而算术平方根表示为
3、求下列各数的平方根:
解:(1)∵
∴121的平方根是±11
即
(2)∵
∴ 的平方根是
即
练一练
平方与
开平方
互为逆运算
3、求下列各数的平方根:
解:(3)∵
∴0.0025的平方根是±0.05,
即
练一练
(4)∵
∴
的平方根是
即
方法
总结
求一个非负数的平方根,只要找出一个非负数,使得它的平方等于这个数,那么找出的那个非负数,连同它的相反数,就是所求的平方根
例3.说出下列各式的意义,并计算:
解:
表示 的算术平方根,
表示 的算术平方根,
例题 精讲
例3.说出下列各式表示的意义,并计算:
解:
表示 的负的平方根,
表示 的算术平方根,
例题 精讲
能力提升
1、已知2a-1和a+4是一个正数m的两个平方根,则a= ,m= .
分析:正数有两个平方根,并且互为相反数。
互为相反数两数和为0.
由2a-1+a+4=0得a的值,
代入得2a-1的值,
作2a-1的平方得m的值。
解:由2a-1+a+4=0得a=-1,
所以2a-1=-3
所以m=
能力提升
2、若 ,则abc= .
分析:几个非负数的和为零,则每个非负数都为零。
得a=-2,b=-5,c=4,得abc=40
解:由题得
所以a=-2,b=-5,c=4
所以abc=
概念及表示方法
A
B
式子有意义的条件
C
求非负数的(算术)平方根
E
非负性的运用
D
已知一个数的算术平方根,求原数
课堂总结
平方根
布置 作业
必做题习题6.1第1,2,5
选做题《同步学习》P2:7、8
