沪科版数学七年级下册 8.3 完全平方公式与平方差公式课件(共19张PPT)
文档属性
| 名称 | 沪科版数学七年级下册 8.3 完全平方公式与平方差公式课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 132.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-18 00:00:00 | ||
图片预览






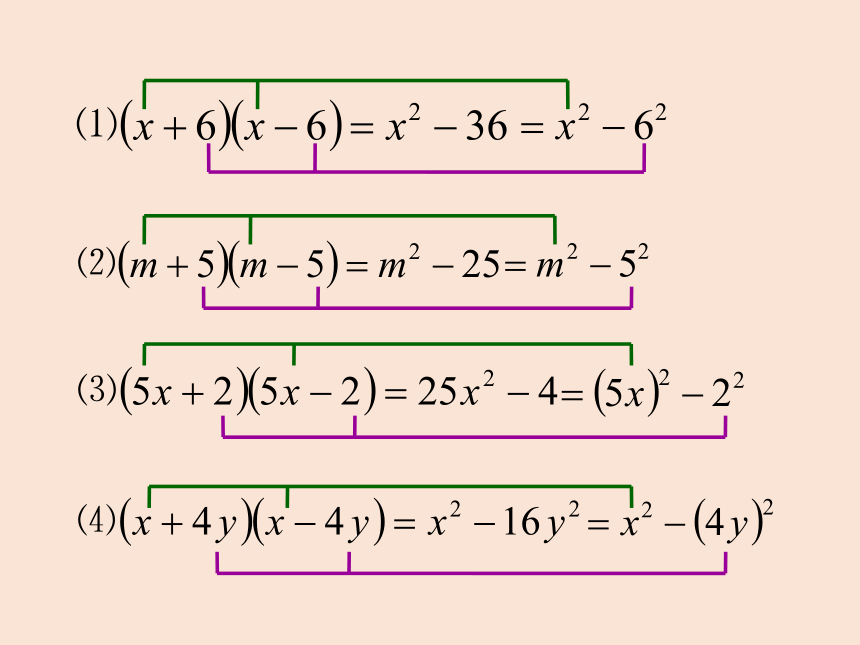
文档简介
(共19张PPT)
8.3 完全平方公式与平方差公式
1.掌握平方差公式的结构特征;
2.正确地运用平方差公式进行计算;
知识与能力
学习目标
过程与方法
在探索平方差公式的过程中,感悟从具体到抽象研究问题的方法;在验证平方差公式的过程中,感知数形结合的思想,进一步发展学生的福好感和推理能力、归纳能力;在运用公式的过程中,渗透转化、建模等数学思想,培养学生的思维能力和数学应用能力。
情感、态度与价值观
让学生在合作探究的学习过程中体验成功的喜悦,培养学生勇于探索、善于观察、大胆猜想的创新思维品质。
理解平方差公式,掌握其结构特点,并能运用公式进行运算。
学习重难点
重点
难点
1.理解公式中的字母的含义,即公式中的字母可以表示具体的数、单项式、多项式、分式、乃至任何代数式。
2.平方差公式的变式应用。
复习旧识:
1.什么是完全平方公式?
两个数的和(或差)的平方,等于这两个数的平方和加(或减)这两个数乘积的2倍。即:
2.计算:
⑴
⑵
在《我是小神童》的智力抢 答中,主持人提供了两道题:
1、
2、
主持人话音刚落,就立刻有一个 学生站起来抢答说:“第一题等 于 396,第二题等于9999。”其 速度之 快,简直就是脱口而出。 同学们,你知 道是如何计算的吗?
计算下列多项式的积.
新知探究
⑴式子的左边有什么共同特征?
⑵式子的右边有什么共同特征?
⑶能不能用字母表示你的发现?
⑷你能对你发现的规律进行推导吗?
⑸你能用一个几何图形验证你的结论吗?
(a+b)(a-b) =
a2-b2
语言表述:
两个数的和与这两个数的差的积,等于这两个数的平方差
平方差公式
新知学习
(a+b)(a b)=a2 b2
(1)公式左边是两个二项式相乘,其中“a和a”是相同项,“b和 b”是相反项。
(2)公式右边是二项式,是相同项平方减去相反项的平方。
(3)公式中的 a和b 可以是数,也可以是代数式.
{
平方差公式的结构特征
(不能)
(不能)
(不能)
(能)
例1 判断下列式子能否用平方差公式计算,为什么?
例2 利用平方差公式计算:
(1)22×18
(1)22×18
=(20+2) ×(20 2 )
=202 22
=400 4
=396
解:
(2)101×99
(2)101×99
=(100 +1) ×(100 1 )
=1002 12
=10000 1
=9999
你的收获?
1.书71页:习题8.3第2题
2.练习册:对应练习
作业
Bye bye
谢 谢
8.3 完全平方公式与平方差公式
1.掌握平方差公式的结构特征;
2.正确地运用平方差公式进行计算;
知识与能力
学习目标
过程与方法
在探索平方差公式的过程中,感悟从具体到抽象研究问题的方法;在验证平方差公式的过程中,感知数形结合的思想,进一步发展学生的福好感和推理能力、归纳能力;在运用公式的过程中,渗透转化、建模等数学思想,培养学生的思维能力和数学应用能力。
情感、态度与价值观
让学生在合作探究的学习过程中体验成功的喜悦,培养学生勇于探索、善于观察、大胆猜想的创新思维品质。
理解平方差公式,掌握其结构特点,并能运用公式进行运算。
学习重难点
重点
难点
1.理解公式中的字母的含义,即公式中的字母可以表示具体的数、单项式、多项式、分式、乃至任何代数式。
2.平方差公式的变式应用。
复习旧识:
1.什么是完全平方公式?
两个数的和(或差)的平方,等于这两个数的平方和加(或减)这两个数乘积的2倍。即:
2.计算:
⑴
⑵
在《我是小神童》的智力抢 答中,主持人提供了两道题:
1、
2、
主持人话音刚落,就立刻有一个 学生站起来抢答说:“第一题等 于 396,第二题等于9999。”其 速度之 快,简直就是脱口而出。 同学们,你知 道是如何计算的吗?
计算下列多项式的积.
新知探究
⑴式子的左边有什么共同特征?
⑵式子的右边有什么共同特征?
⑶能不能用字母表示你的发现?
⑷你能对你发现的规律进行推导吗?
⑸你能用一个几何图形验证你的结论吗?
(a+b)(a-b) =
a2-b2
语言表述:
两个数的和与这两个数的差的积,等于这两个数的平方差
平方差公式
新知学习
(a+b)(a b)=a2 b2
(1)公式左边是两个二项式相乘,其中“a和a”是相同项,“b和 b”是相反项。
(2)公式右边是二项式,是相同项平方减去相反项的平方。
(3)公式中的 a和b 可以是数,也可以是代数式.
{
平方差公式的结构特征
(不能)
(不能)
(不能)
(能)
例1 判断下列式子能否用平方差公式计算,为什么?
例2 利用平方差公式计算:
(1)22×18
(1)22×18
=(20+2) ×(20 2 )
=202 22
=400 4
=396
解:
(2)101×99
(2)101×99
=(100 +1) ×(100 1 )
=1002 12
=10000 1
=9999
你的收获?
1.书71页:习题8.3第2题
2.练习册:对应练习
作业
Bye bye
谢 谢
