沪科版数学七年级下册 第6章 实数复习 课件(共23张PPT)
文档属性
| 名称 | 沪科版数学七年级下册 第6章 实数复习 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 494.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-18 16:20:12 | ||
图片预览






文档简介
(共23张PPT)
第6章 实数 复习课件
有理数
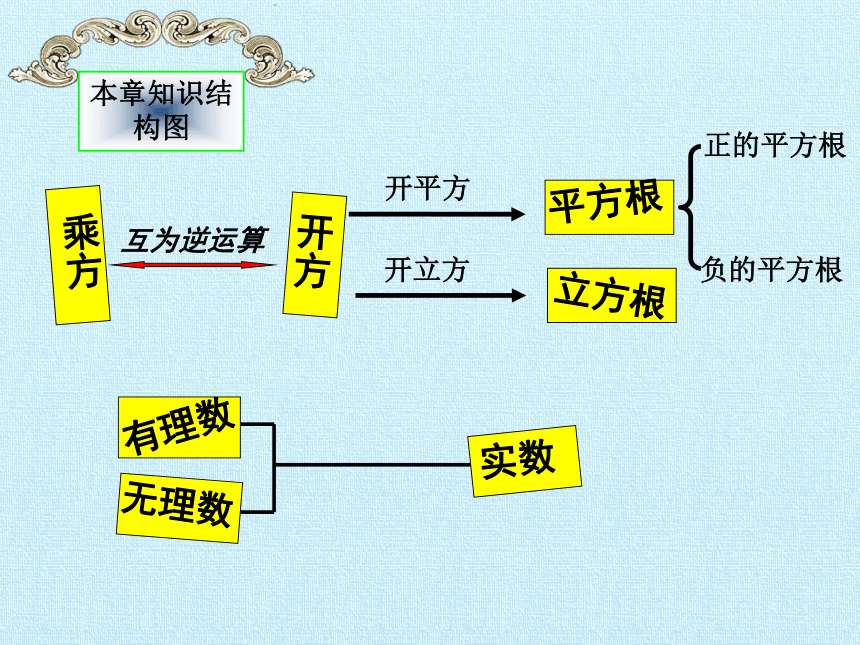
本章知识结构图
乘方
开方
平方根
立方根
无理数
实数
互为逆运算
开平方
开立方
正的平方根
负的平方根
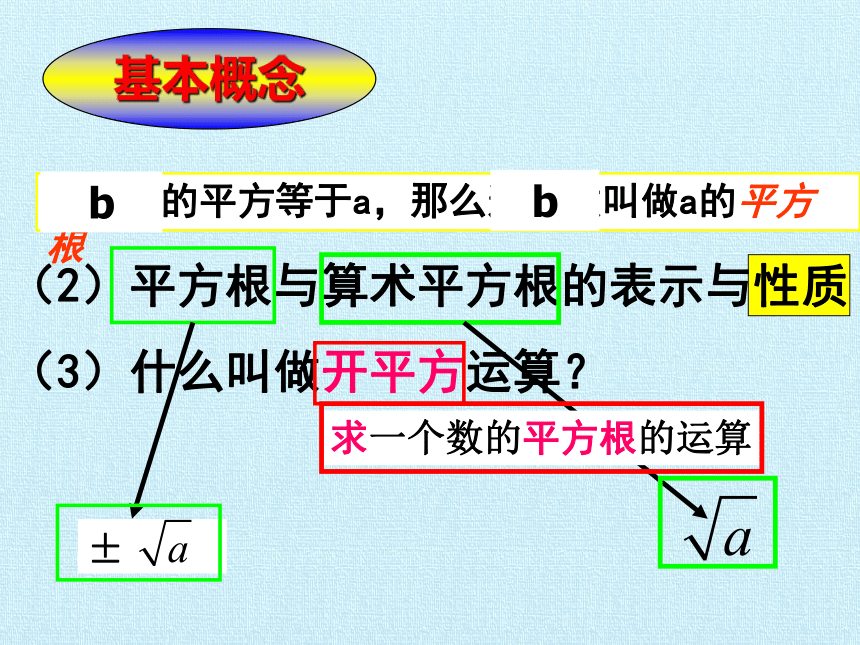
基本概念
(1)平方根与算术平方根的概念
(2)平方根与算术平方根的表示与性质
(3)什么叫做开平方运算?
一个数的平方等于a,那么这个数叫做a的平方根
b
b
±
求一个数的平方根的运算
基本概念
(1)立方根的概念
(2)立方根表示与性质
(3)什么叫做开立方运算?
一个数的立方等于a,那么这个数叫做a的立方根
求一个数的立方根的运算
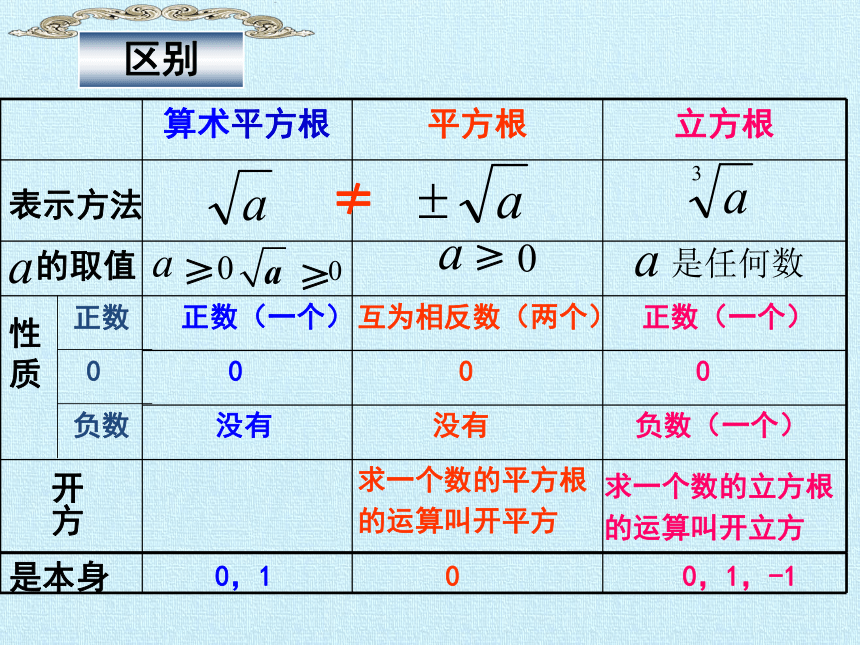
算术平方根 平方根 立方根
表示方法
的取值
性质
≥
开方
≥
正数
0
负数
正数(一个)
0
没有
互为相反数(两个)
0
没有
正数(一个)
0
负数(一个)
求一个数的平方根
的运算叫开平方
求一个数的立方根
的运算叫开立方
≠
是本身
0,1
0
0,1,-1
区别
≥
一、填空:
3、若一个数只有一个平方根,则这个数是 ,它的立方根是 ;
开平方
0
0
开立方
3
5、若某数的一个立方根是4,则这个数的平方根是 ;
±8
6、(-4)2的算术平方根是 ;
4
±3
9、-64的立方根是 ;
-4
±5
4
-4
解下列方程:
练习
掌握规律
练习
1、求下列各数的平方根与算术平方根
2、求下列各数的立方根
计算:
3
3
0
4.5
-3
3
=
总结:
实数
有理数
无理数
分数
整数
正整数
0
负整数
正分数
负分数
自然数
正无理数
负无理数
无限不循环小数
有限小数及无限循环小数
一般有三种情况
1.将下列各数分别填入下列的集合括号中
自然数集合:
整数集合:
有理数集合:
无理数集合:
…
…
…
练习
0
1
-1
B
2
A
2
(1)如何在数轴上画出
表示 2的点。
(3)每一个实数都可以用数轴上的点来表示;
反过来,数轴上的每一个点都表示一个实数。
(2)所有的有理数能在轴上表示出来,
但有理数并不能概括数轴上所有的点。
即:实数和数轴上的点是一一对应的!
绝对值、相反数、倒数以及有理数运算律
在实数的运算中,仍然成立
注意
是负数
等于它的相反数
是正数
等于本身
里面的数的符号
化简绝对值要看
3.
大家都知道 是无理数,而无理数是无限不循环小数,因此, 的小数部分我们不可能全部写出来,于是小明用 来表示 的小数部分,你同意小明的方法吗?事实上,小明的表示方法是有道理的,因为 的整数部分是1,将这个数减去其整数部分,差就是小数部分。请解答:
思考探究题
4.π的整数部分为___,则它的小数部分是 ;
π-3
3
5. 的整数部分是___,小数部分是______。
2
数轴上两点A,B分别表示实数 和
,求A,B两点之间的距离。
6.
应用题
1. 将一个体积是216cm2立方体木块锯成8个同样大小的立方体小木块,每个小立方体的表面积是多少?
2.要做一个正方形使它的面积等于半径为20cm的圆的面积,则做成的木料的边长是 cm
谢 谢
第6章 实数 复习课件
有理数
本章知识结构图
乘方
开方
平方根
立方根
无理数
实数
互为逆运算
开平方
开立方
正的平方根
负的平方根
基本概念
(1)平方根与算术平方根的概念
(2)平方根与算术平方根的表示与性质
(3)什么叫做开平方运算?
一个数的平方等于a,那么这个数叫做a的平方根
b
b
±
求一个数的平方根的运算
基本概念
(1)立方根的概念
(2)立方根表示与性质
(3)什么叫做开立方运算?
一个数的立方等于a,那么这个数叫做a的立方根
求一个数的立方根的运算
算术平方根 平方根 立方根
表示方法
的取值
性质
≥
开方
≥
正数
0
负数
正数(一个)
0
没有
互为相反数(两个)
0
没有
正数(一个)
0
负数(一个)
求一个数的平方根
的运算叫开平方
求一个数的立方根
的运算叫开立方
≠
是本身
0,1
0
0,1,-1
区别
≥
一、填空:
3、若一个数只有一个平方根,则这个数是 ,它的立方根是 ;
开平方
0
0
开立方
3
5、若某数的一个立方根是4,则这个数的平方根是 ;
±8
6、(-4)2的算术平方根是 ;
4
±3
9、-64的立方根是 ;
-4
±5
4
-4
解下列方程:
练习
掌握规律
练习
1、求下列各数的平方根与算术平方根
2、求下列各数的立方根
计算:
3
3
0
4.5
-3
3
=
总结:
实数
有理数
无理数
分数
整数
正整数
0
负整数
正分数
负分数
自然数
正无理数
负无理数
无限不循环小数
有限小数及无限循环小数
一般有三种情况
1.将下列各数分别填入下列的集合括号中
自然数集合:
整数集合:
有理数集合:
无理数集合:
…
…
…
练习
0
1
-1
B
2
A
2
(1)如何在数轴上画出
表示 2的点。
(3)每一个实数都可以用数轴上的点来表示;
反过来,数轴上的每一个点都表示一个实数。
(2)所有的有理数能在轴上表示出来,
但有理数并不能概括数轴上所有的点。
即:实数和数轴上的点是一一对应的!
绝对值、相反数、倒数以及有理数运算律
在实数的运算中,仍然成立
注意
是负数
等于它的相反数
是正数
等于本身
里面的数的符号
化简绝对值要看
3.
大家都知道 是无理数,而无理数是无限不循环小数,因此, 的小数部分我们不可能全部写出来,于是小明用 来表示 的小数部分,你同意小明的方法吗?事实上,小明的表示方法是有道理的,因为 的整数部分是1,将这个数减去其整数部分,差就是小数部分。请解答:
思考探究题
4.π的整数部分为___,则它的小数部分是 ;
π-3
3
5. 的整数部分是___,小数部分是______。
2
数轴上两点A,B分别表示实数 和
,求A,B两点之间的距离。
6.
应用题
1. 将一个体积是216cm2立方体木块锯成8个同样大小的立方体小木块,每个小立方体的表面积是多少?
2.要做一个正方形使它的面积等于半径为20cm的圆的面积,则做成的木料的边长是 cm
谢 谢
