沪科版数学七年级下册 10.2 平行线 课件(共19张PPT)
文档属性
| 名称 | 沪科版数学七年级下册 10.2 平行线 课件(共19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-18 20:08:37 | ||
图片预览




文档简介
(共20张PPT)
10. 2.1 平行线
1、飞机的喷雾、铁路的双轨以及桥上 的装饰都有怎样的位置关系呢?
2、在实际生活中,有很多两条直线平行的实例,你能举例说明吗?
短池游泳
双杠
橱柜
灭蚊灯管
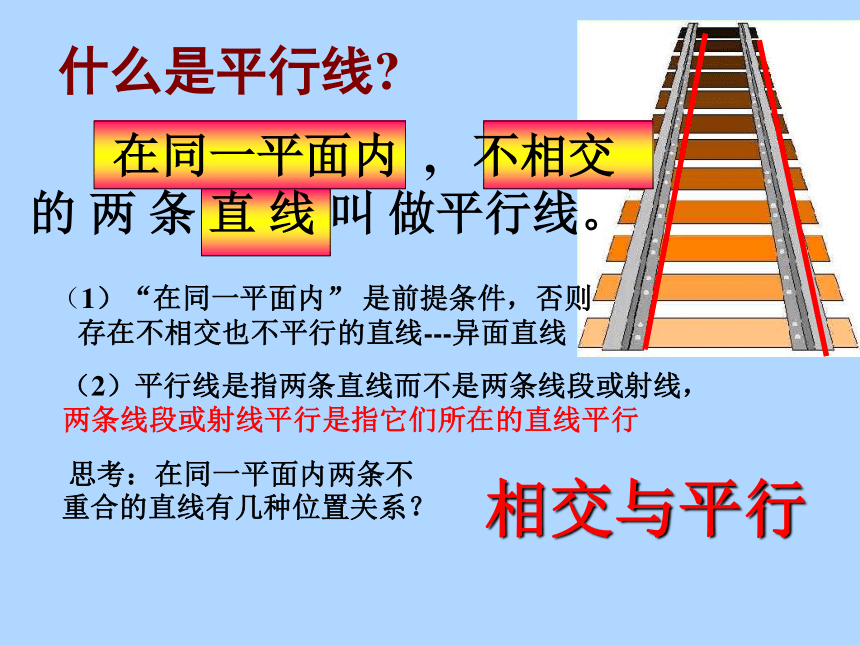
什么是平行线
在同一平面内 , 不相交的 两 条 直 线 叫 做平行线。
(1)“在同一平面内” 是前提条件,否则存在不相交也不平行的直线---异面直线
(2)平行线是指两条直线而不是两条线段或射线,两条线段或射线平行是指它们所在的直线平行
思考:在同一平面内两条不重合的直线有几种位置关系?
相交与平行
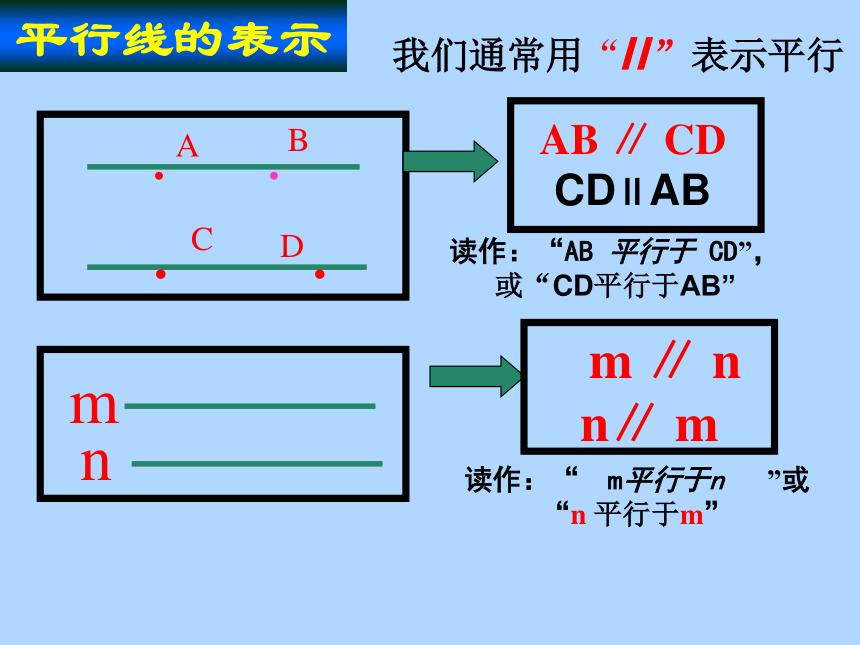
我们通常用“//”表示平行
平行线的表示
C
D
B
A
·
·
·
·
m ∥ n n∥ m
AB ∥ CD CD∥AB
m
n
读作:“AB 平行于 CD”, 或“CD平行于AB”
读作:“ m平行于n ”或“n 平行于m”
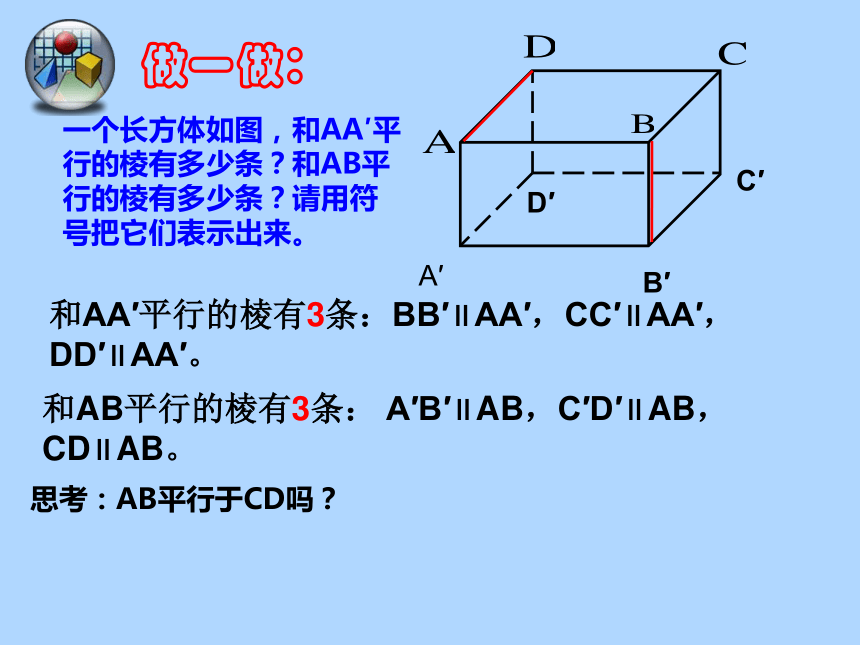
一个长方体如图,和AA′平行的棱有多少条?和AB平行的棱有多少条?请用符号把它们表示出来。
A′
B′
C′
D′
和AA′平行的棱有3条:BB′∥AA′,CC′∥AA′,DD′∥AA′。
和AB平行的棱有3条: A′B′∥AB,C′D′∥AB,CD∥AB。
做一做:
思考:AB平行于CD吗?
给你一条直线AB,你会画它的平行线吗?你可以画多少条?
A
B
画一画:
一、贴
二、靠
三、推
四、画
平行线的画法:
“推平行线法”:
(2)已知直线AB和直线外一点P,你能过点P画一条直线与直线AB平行吗?这样的直线能画多少条?
A
B
C
C
A
B
平行线的基本事实:
经过直线外一点,有且只有一条直线与这条直线平行.
说明:人们在长期实践中总结出来的结论叫基本事实,也称为公理,它可以作为以后推理的依据.
(3)在直线AB和CD外还有一点E,过点E作AB的平行线
C
A
B
E
D
F
想一想:直线CD与EF 有什么位置关系?可能相交吗?为什么?
已知:AB∥CD, AB∥EF
如图:AB∥CD, AB ∥EF,求证CD与EF不相交?
A
B
C
D
E
F
P
证明:假设EF与CD相交与P点,如图所示
那么:过点P有两条直线CD,EF都与AB平行,
与平行性质相矛盾
所以直线CD与EF不能相交,只能平行。
如果两条直线都和第三条直线平行,那么这两条直线也互相平行。
平行线性质的推论
∵a∥b b∥c
∴a∥c
(平行公理的推论)
(已知)
符号语言:
a
c
b
∵a∥b b∥c
练习:一、读下列语句,并画出图形.
如图在∠AOB内取一点P,过点P画PC ∥ OA交OB于C.
(2)
.
P
F
C
二、如图,在同一平面内AB∥CD,EF与AB相交于P点,EF能与CD平行吗?为什么?
C
D
A
B
E
F
P
小结:
本节课你的收获是什么?
(1)什么是平行线;
(2)平行线的画法;
(3)平行线的表示方法;
(4)平行线的性质。
必做:课本128页习题1、2两题
选做:
作业
利用所学平行知识,设计一幅优美的图案,并配上说明。
10. 2.1 平行线
1、飞机的喷雾、铁路的双轨以及桥上 的装饰都有怎样的位置关系呢?
2、在实际生活中,有很多两条直线平行的实例,你能举例说明吗?
短池游泳
双杠
橱柜
灭蚊灯管
什么是平行线
在同一平面内 , 不相交的 两 条 直 线 叫 做平行线。
(1)“在同一平面内” 是前提条件,否则存在不相交也不平行的直线---异面直线
(2)平行线是指两条直线而不是两条线段或射线,两条线段或射线平行是指它们所在的直线平行
思考:在同一平面内两条不重合的直线有几种位置关系?
相交与平行
我们通常用“//”表示平行
平行线的表示
C
D
B
A
·
·
·
·
m ∥ n n∥ m
AB ∥ CD CD∥AB
m
n
读作:“AB 平行于 CD”, 或“CD平行于AB”
读作:“ m平行于n ”或“n 平行于m”
一个长方体如图,和AA′平行的棱有多少条?和AB平行的棱有多少条?请用符号把它们表示出来。
A′
B′
C′
D′
和AA′平行的棱有3条:BB′∥AA′,CC′∥AA′,DD′∥AA′。
和AB平行的棱有3条: A′B′∥AB,C′D′∥AB,CD∥AB。
做一做:
思考:AB平行于CD吗?
给你一条直线AB,你会画它的平行线吗?你可以画多少条?
A
B
画一画:
一、贴
二、靠
三、推
四、画
平行线的画法:
“推平行线法”:
(2)已知直线AB和直线外一点P,你能过点P画一条直线与直线AB平行吗?这样的直线能画多少条?
A
B
C
C
A
B
平行线的基本事实:
经过直线外一点,有且只有一条直线与这条直线平行.
说明:人们在长期实践中总结出来的结论叫基本事实,也称为公理,它可以作为以后推理的依据.
(3)在直线AB和CD外还有一点E,过点E作AB的平行线
C
A
B
E
D
F
想一想:直线CD与EF 有什么位置关系?可能相交吗?为什么?
已知:AB∥CD, AB∥EF
如图:AB∥CD, AB ∥EF,求证CD与EF不相交?
A
B
C
D
E
F
P
证明:假设EF与CD相交与P点,如图所示
那么:过点P有两条直线CD,EF都与AB平行,
与平行性质相矛盾
所以直线CD与EF不能相交,只能平行。
如果两条直线都和第三条直线平行,那么这两条直线也互相平行。
平行线性质的推论
∵a∥b b∥c
∴a∥c
(平行公理的推论)
(已知)
符号语言:
a
c
b
∵a∥b b∥c
练习:一、读下列语句,并画出图形.
如图在∠AOB内取一点P,过点P画PC ∥ OA交OB于C.
(2)
.
P
F
C
二、如图,在同一平面内AB∥CD,EF与AB相交于P点,EF能与CD平行吗?为什么?
C
D
A
B
E
F
P
小结:
本节课你的收获是什么?
(1)什么是平行线;
(2)平行线的画法;
(3)平行线的表示方法;
(4)平行线的性质。
必做:课本128页习题1、2两题
选做:
作业
利用所学平行知识,设计一幅优美的图案,并配上说明。
