人教版数学七年级下册 6.1平方根 课件(共19张PPT)
文档属性
| 名称 | 人教版数学七年级下册 6.1平方根 课件(共19张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 534.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-18 23:05:41 | ||
图片预览





文档简介
(共22张PPT)
回顾
说出下列各式的意义,并说出它们的值
√
25
√
1
4
√
0
1. 算术平方根的定义是什么呢?针对什么数而言?
2.算术平方根的性质是什么呢?
一个数的平方是9,
那么这个数是什么数?
所以这个数是3或-3.
(简记为±3)
平方根
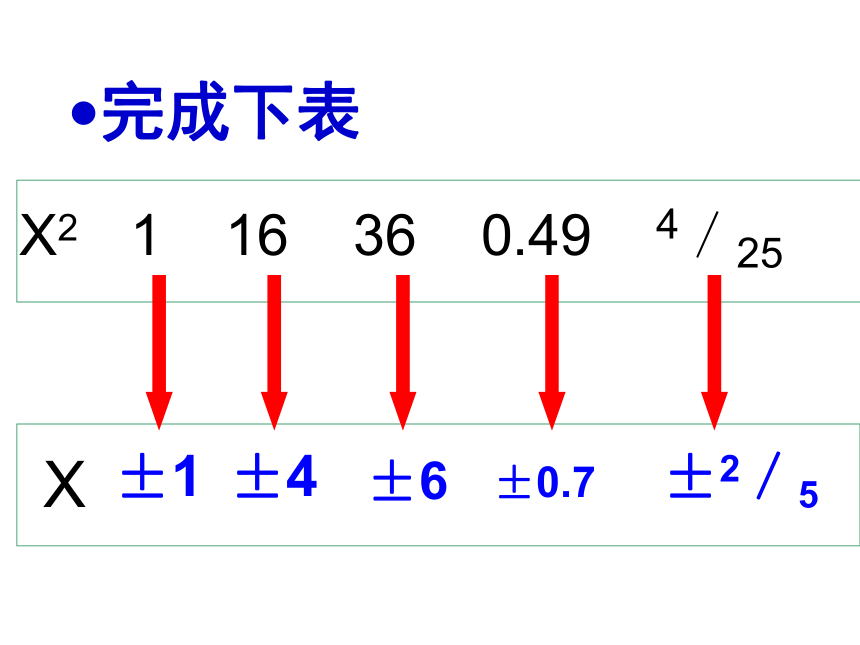
完成下表
X2 1 16 36 0.49 4/25
X
±1
±6
±0.7
±2/5
±4
就是说,如果 ,那么x就叫做a的平方根.
一般地,如果一个数的平方等于a,这个数就叫做 a的平方根(二次方根).
一、平方根:
表示方法
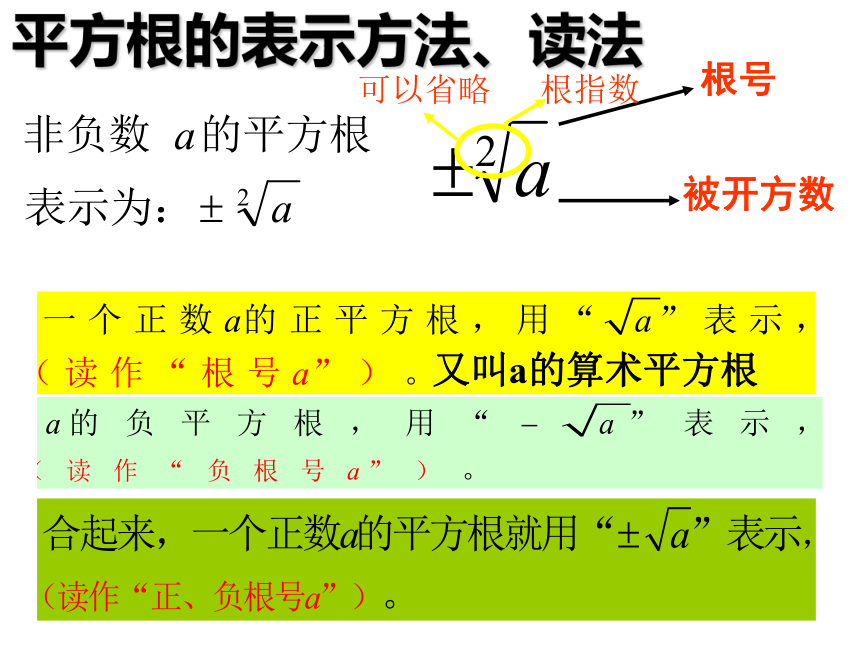
平方根的表示方法、读法
根号
被开方数
根指数
可以省略
又叫a的算术平方根
例 . 求下列各数的平方根:
(1)81;(2) ; (3)0.49; (4)
解:(1)∵ (±9)2=81,
(2)
的平方根是 ,
(3)∵(±0.7)2=0.49,
∴0.49的平方根为±0.7.
即
∴81的平方根为±9.
即:
即
(5)0
(6)-1
原数 81 0 (-25)2 11 a
算术平方根
平方根
例1:填表
9
0
±
25
±
±9
0
±25
±
(a≥0)
平方根的性质
1.正数有两个平方根,而且它们互为相反数。其中正的平方根就是算术平方根。
2.0有一个平方根是0.
3.负数没有平方根。
思考:
±6
3
±2
注意要化到最简才能求
观察 讨论
+1
-1
+2
-2
+3
-3
X
1
4
9
平方运算
X2
开平方运算
1
4
9
+1
-1
+2
-2
+3
-3
x2
X
自学并讨论?
什么叫开平方?见45页
求一个数a的平方根的运算,叫做开平方.
开平方与平方是什么关系?见P45
a的平方根
底数
幂
被开方数
互为
逆运算
指数
根号
平方运算
开平方运算
说出下列各式的含义,求下列各式的值:
1) 2)
3) 4)
—
(-7)2
+1
1、下列各数是否有平方根,
为什么?
① 22 ② 0
③ -0.01 ④ (-3)2
仔细看一看
4) 的平方根是 ± 4 ( )
看谁反应快
1) 1.21 的平方根是 ± 1.1 ( )
2) 9 的平方根是 3 ( )
3) -5 是 25 的平方根 ( )
5) 平方根是本身的数有0 ,1 ( )
√
×
×
×
√
例4:求下列各式中的x:
(1) x =16
(3)(x-1)2=25
(2) 4x =81
(1)若a+1没有平方根,那么a的范围是 。
(2)若4a+1的平方根是±5,则a=( )
(3)一个正数x的平方根等于m+1和m-3,
求x=( )和m=( ).
a﹤-1
1.若根号x+2=2,求2x+5的平方根。
2.有一个正数的平方根分别是2a-3与5-a,求这个数。
3.a为根号170的整数部分,b-1是400的算术平方根,求根号a+b.
挑战思维
回顾
说出下列各式的意义,并说出它们的值
√
25
√
1
4
√
0
1. 算术平方根的定义是什么呢?针对什么数而言?
2.算术平方根的性质是什么呢?
一个数的平方是9,
那么这个数是什么数?
所以这个数是3或-3.
(简记为±3)
平方根
完成下表
X2 1 16 36 0.49 4/25
X
±1
±6
±0.7
±2/5
±4
就是说,如果 ,那么x就叫做a的平方根.
一般地,如果一个数的平方等于a,这个数就叫做 a的平方根(二次方根).
一、平方根:
表示方法
平方根的表示方法、读法
根号
被开方数
根指数
可以省略
又叫a的算术平方根
例 . 求下列各数的平方根:
(1)81;(2) ; (3)0.49; (4)
解:(1)∵ (±9)2=81,
(2)
的平方根是 ,
(3)∵(±0.7)2=0.49,
∴0.49的平方根为±0.7.
即
∴81的平方根为±9.
即:
即
(5)0
(6)-1
原数 81 0 (-25)2 11 a
算术平方根
平方根
例1:填表
9
0
±
25
±
±9
0
±25
±
(a≥0)
平方根的性质
1.正数有两个平方根,而且它们互为相反数。其中正的平方根就是算术平方根。
2.0有一个平方根是0.
3.负数没有平方根。
思考:
±6
3
±2
注意要化到最简才能求
观察 讨论
+1
-1
+2
-2
+3
-3
X
1
4
9
平方运算
X2
开平方运算
1
4
9
+1
-1
+2
-2
+3
-3
x2
X
自学并讨论?
什么叫开平方?见45页
求一个数a的平方根的运算,叫做开平方.
开平方与平方是什么关系?见P45
a的平方根
底数
幂
被开方数
互为
逆运算
指数
根号
平方运算
开平方运算
说出下列各式的含义,求下列各式的值:
1) 2)
3) 4)
—
(-7)2
+1
1、下列各数是否有平方根,
为什么?
① 22 ② 0
③ -0.01 ④ (-3)2
仔细看一看
4) 的平方根是 ± 4 ( )
看谁反应快
1) 1.21 的平方根是 ± 1.1 ( )
2) 9 的平方根是 3 ( )
3) -5 是 25 的平方根 ( )
5) 平方根是本身的数有0 ,1 ( )
√
×
×
×
√
例4:求下列各式中的x:
(1) x =16
(3)(x-1)2=25
(2) 4x =81
(1)若a+1没有平方根,那么a的范围是 。
(2)若4a+1的平方根是±5,则a=( )
(3)一个正数x的平方根等于m+1和m-3,
求x=( )和m=( ).
a﹤-1
1.若根号x+2=2,求2x+5的平方根。
2.有一个正数的平方根分别是2a-3与5-a,求这个数。
3.a为根号170的整数部分,b-1是400的算术平方根,求根号a+b.
挑战思维
