人教版八年级下册第十二章简单机械单元练习(有答案)
文档属性
| 名称 | 人教版八年级下册第十二章简单机械单元练习(有答案) |  | |
| 格式 | docx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-04-18 08:46:34 | ||
图片预览


文档简介
人教版八年级下册 第十二章 简单机械 单元练习
一、单选题
1.下列关于定滑轮的说法正确的是( )
A.使用定滑轮可以省距离 B.使用定滑轮可以省力
C.使用定滑轮可以改变拉力方向 D.使用定滑轮可以省功
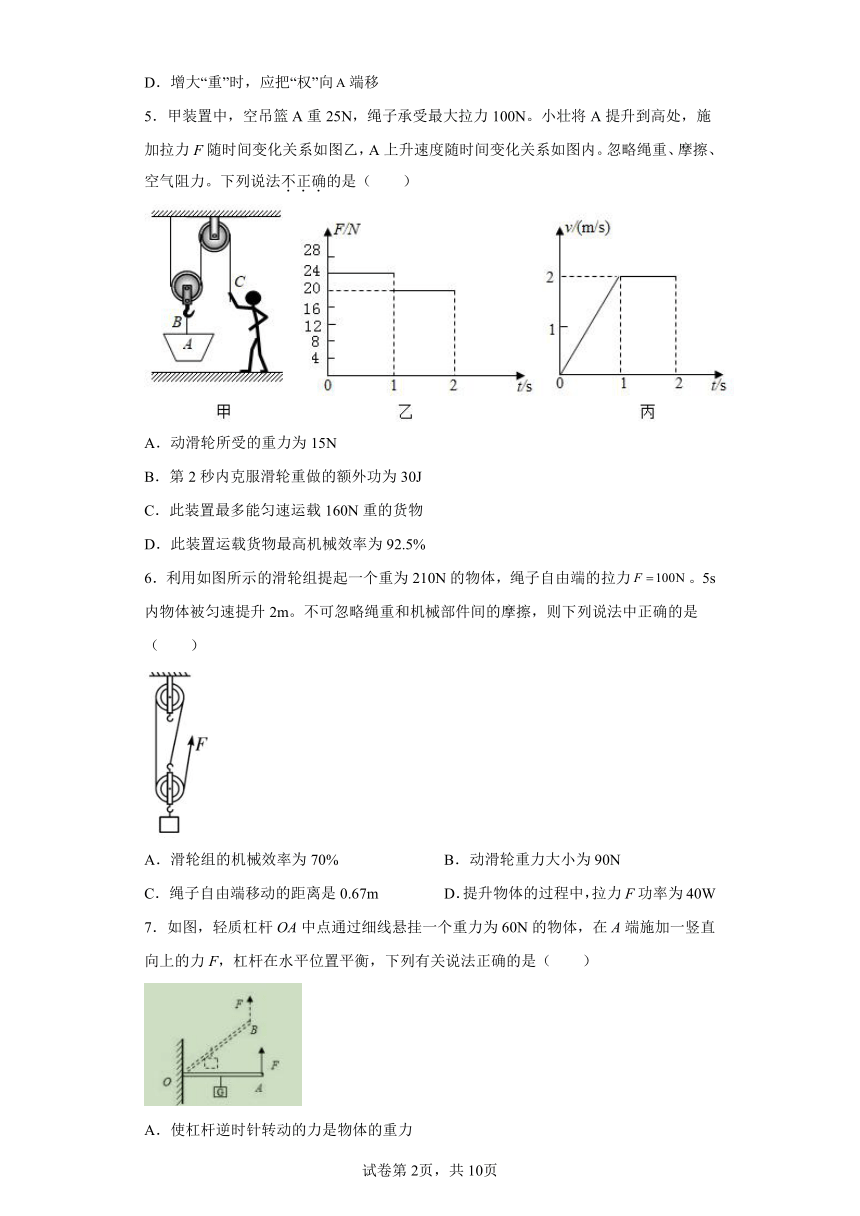
2.在图中,物体A的重力为G,在拉力F的作用下,物体沿水平桌面做匀速直线运动,已知物体受到的摩擦力为f,则人对绳的拉力F的大小等于( )
A.0.5G B.2G C.0.5f D.2f
3.用如图所示的滑轮组提升重物时(忽略绳重及摩擦),下列做法能提高滑轮组机械效率的有
A.增加物体被提升的高度
B.增大动滑轮的重力
C.改变绳子的绕法,减少承担重物的绳子的段数
D.增加物体的重力
4.如图所示,是我国古代《墨经》最早记述了秤的杠杆原理,有关它的说法正确的是( )
A.“标”“本”表示力,“权”“重”表示力臂
B.图中的点为杠杆的支点
C.“权”小于“重”时,端一定上扬
D.增大“重”时,应把“权”向端移
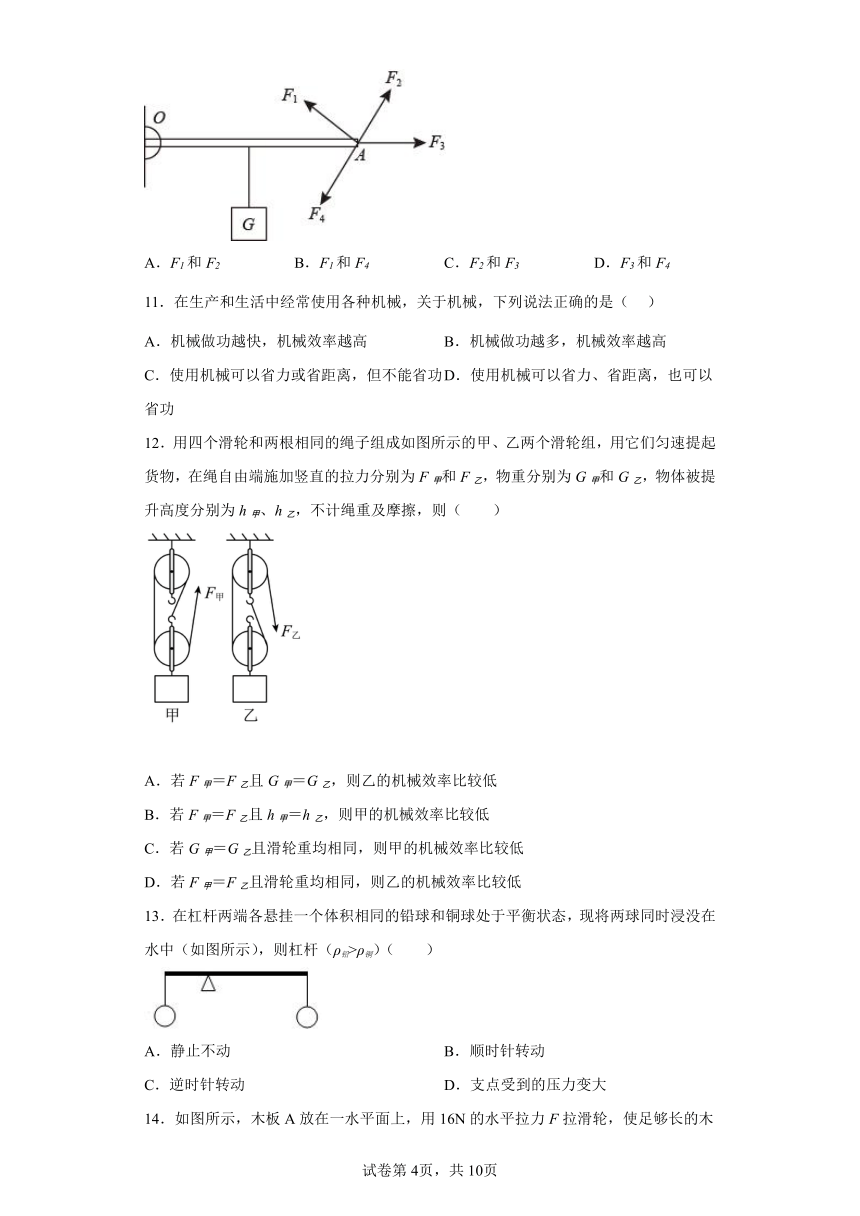
5.甲装置中,空吊篮A重25N,绳子承受最大拉力100N。小壮将A提升到高处,施加拉力F随时间变化关系如图乙,A上升速度随时间变化关系如图内。忽略绳重、摩擦、空气阻力。下列说法不正确的是( )
A.动滑轮所受的重力为15N
B.第2秒内克服滑轮重做的额外功为30J
C.此装置最多能匀速运载160N重的货物
D.此装置运载货物最高机械效率为92.5%
6.利用如图所示的滑轮组提起一个重为210N的物体,绳子自由端的拉力。5s内物体被匀速提升2m。不可忽略绳重和机械部件间的摩擦,则下列说法中正确的是( )
A.滑轮组的机械效率为70% B.动滑轮重力大小为90N
C.绳子自由端移动的距离是0.67m D.提升物体的过程中,拉力F功率为40W
7.如图,轻质杠杆OA中点通过细线悬挂一个重力为60N的物体,在A端施加一竖直向上的力F,杠杆在水平位置平衡,下列有关说法正确的是( )
A.使杠杆逆时针转动的力是物体的重力
B.此杠杆为费力杠杆
C.杠杆处于水平位置平衡时拉力F的大小为30N
D.保持F的方向竖直向上不变,将杠杆从A位置匀速提升到B位置的过程中,力F将增大
8.下列机械中,使用时不能省力但能省距离的是( )
A. 自行车的脚踏装置
B. 盘山公路
C. 划船用的浆
D. 道钉撬
9.如图所示,小明用滑轮组提升物体A,物体A重7N,定滑轮重2N,动滑轮重1N.物体A在1s内沿竖直方向匀速升高了0.2m.不计绳重和轮与轴的摩擦,下列说法中正确的是
A.绳子自由端受到的拉力大小是 3N
B.滑轮组的机械效率为 87.5%
C.有用功为 1.6J
D.拉力 F 做功的功率为 0.8W
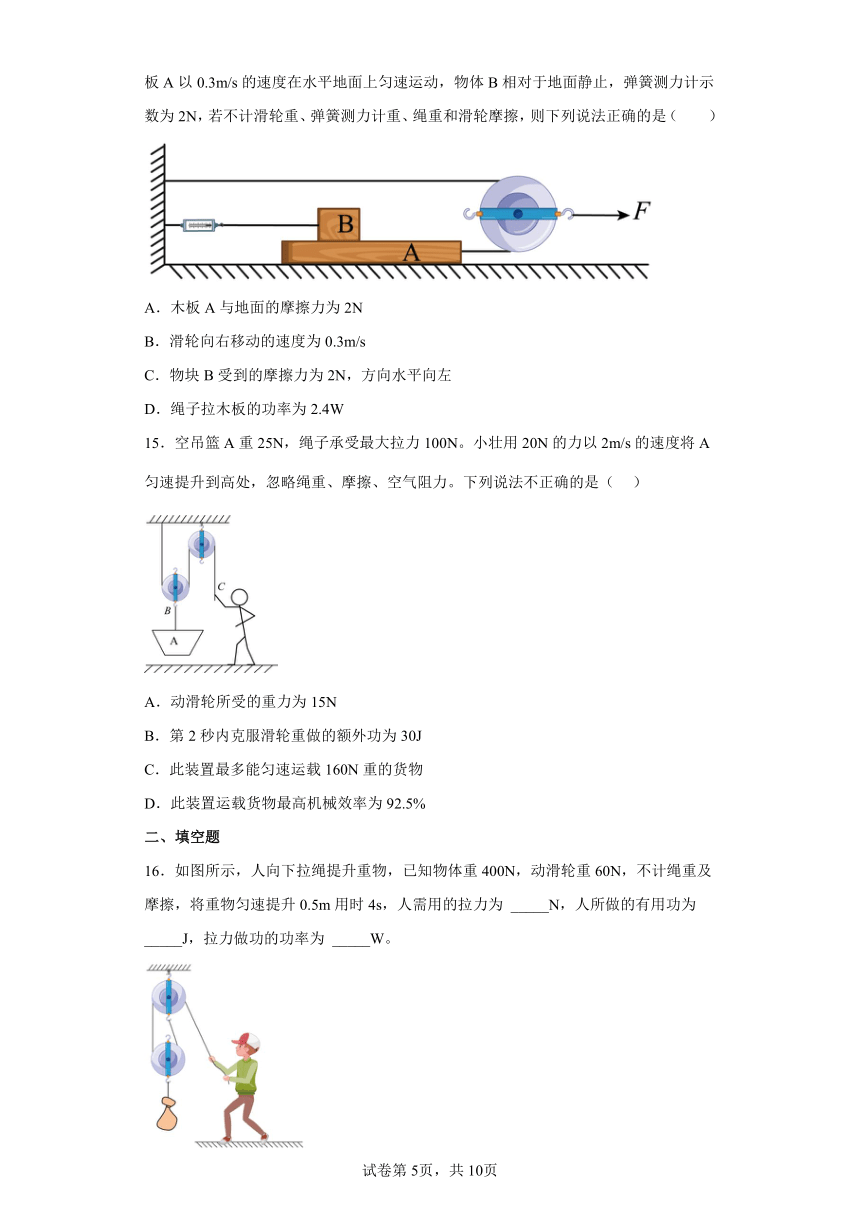
10.如图所示,轻质杠杆可绕支点O自由转动,作用在A点处的各个拉力中,不可能使杠杆水平平衡的是( )
A.F1和F2 B.F1和F4 C.F2和F3 D.F3和F4
11.在生产和生活中经常使用各种机械,关于机械,下列说法正确的是( )
A.机械做功越快,机械效率越高 B.机械做功越多,机械效率越高
C.使用机械可以省力或省距离,但不能省功 D.使用机械可以省力、省距离,也可以省功
12.用四个滑轮和两根相同的绳子组成如图所示的甲、乙两个滑轮组,用它们匀速提起货物,在绳自由端施加竖直的拉力分别为F甲和F乙,物重分别为G甲和G乙,物体被提升高度分别为h甲、h乙,不计绳重及摩擦,则( )
A.若F甲=F乙且G甲=G乙,则乙的机械效率比较低
B.若F甲=F乙且h甲=h乙,则甲的机械效率比较低
C.若G甲=G乙且滑轮重均相同,则甲的机械效率比较低
D.若F甲=F乙且滑轮重均相同,则乙的机械效率比较低
13.在杠杆两端各悬挂一个体积相同的铅球和铜球处于平衡状态,现将两球同时浸没在水中(如图所示),则杠杆(ρ铅>ρ铜)( )
A.静止不动 B.顺时针转动
C.逆时针转动 D.支点受到的压力变大
14.如图所示,木板A放在一水平面上,用16N的水平拉力F拉滑轮,使足够长的木板A以0.3m/s的速度在水平地面上匀速运动,物体B相对于地面静止,弹簧测力计示数为2N,若不计滑轮重、弹簧测力计重、绳重和滑轮摩擦,则下列说法正确的是( )
A.木板A与地面的摩擦力为2N
B.滑轮向右移动的速度为0.3m/s
C.物块B受到的摩擦力为2N,方向水平向左
D.绳子拉木板的功率为2.4W
15.空吊篮A重25N,绳子承受最大拉力100N。小壮用20N的力以2m/s的速度将A匀速提升到高处,忽略绳重、摩擦、空气阻力。下列说法不正确的是( )
A.动滑轮所受的重力为15N
B.第2秒内克服滑轮重做的额外功为30J
C.此装置最多能匀速运载160N重的货物
D.此装置运载货物最高机械效率为92.5%
二、填空题
16.如图所示,人向下拉绳提升重物,已知物体重400N,动滑轮重60N,不计绳重及摩擦,将重物匀速提升0.5m用时4s,人需用的拉力为 _____N,人所做的有用功为 _____J,拉力做功的功率为 _____W。
17.如图所示,物体A重100N,物体B重10N,此时A沿着水平桌面以0.2m/s的速度向右做匀速直线运动(不计摩擦、绳重及滑轮重),那么物体B匀速下降的速度是___________m/s,物体A与水平面间的摩擦力是___________N。
18.小明为了把水平地面上重为200N的木箱移到1m高的平台上,搭建了长为2m斜面。如图所示,现对木箱施加平行于斜面的大小为120N的拉力,将其由底端以0.2m/s的速度匀速拉到顶端。在此过程中拉力做功______J,拉力的功率为______W,斜面的机械效率为______,摩擦力大小为______N。
19.如图所示,小明分别使用甲、乙图中两种不同的机械将同一物体M匀速提升同样高度。测得两次拉力F甲、F乙和物体M所受的重力G如下表所示。当使用乙机械时,测得绳子自由端移动的距离是物体M上升高度的2倍。
(1)从表中数据可知:甲机械________(选填“省力”“费力”或“不省力也不费力”),甲机械所做的有用功_______(选填“大于”“等于”或“小于”)乙机械所做的有用功:
(2)乙提升物体M时的机械效率是________
F甲 F乙 GM
10N 5N 8N
20.如图所示为某磅秤的结构示意图,物体W放在平台上,物体以及平台的重量由刀口A和E分担,并通过由DF、FC、BG、GO、OQ等轻质硬杆组成的杠杆组(自重不计)的作用由Q处悬挂的砝码表示出来。该秤的结构装置中B和D也为刀口,O、G、C、F处为光滑铰链,P为OQ杆的固定转动轴,P、D同在一竖直线上,Q、C、F同在另一竖直线上。已知:AB=L1,BC=L2,DE=L3,DF=L4,OP=L5。若物体W放在平台上的某一位置时,刀口A和E的受力相等,此时砝码的质量为m,T型平台的质量为M,则物体W的质量为______,若物体W不论放在平台上什么位置,秤的示数不变,则L1、L2、L3、L4之间应有的关系为______。
三、综合题
21.质量忽略不计的AC硬棒能绕O点转动,在C点挂一物体,在B点施加动力F时,棒刚好处于静止状态。
(1)画出F2的力臂______;
(2)在B点画出作用在杠杆上最小的动力F1;______
(3)此杠杆是______杠杆。(填:“省力”、“费力”或“等臂”)
判断依据是:______。
22.如图所示,一把杆秤不计自重,秤砣的质量为100g,秤杆水平静止时,OA=5cm, OB=25cm。求∶
(1)被测物体的质量;( )
(2)若秤杆长60cm,不改变OA的长度,则这把秤最大能称量多少千克的物体?( )
(3)若秤砣有缺损时,则杆秤所示的质量会比真实值______(“偏大”或“偏小”)。
23.如图所示,小明分别使用甲、乙、丙三种机械匀速提升物体M(绳长不变),测得拉力和物体M所受的重力如表所示,
(1)在甲图中,作出F1的力臂L1___________。
(2)三种机械中,提升物体M时会费力的有___________(选填“甲”、“乙”、“丙”)
(3)如图所示,丙图中,物体在F3的作用下,沿斜面匀速运动了s,F3对物体做的功为W3;丁图中,物体在F4的作用下,匀速提升至相同高度h时,F4对物体所做的功为W4;戊图中,物体在F5的作用下,在与斜面粗糙程度相同的水平面上,匀速直线运动了,F5对物体所做的功为W5,则该斜面的机械效率___________。(利用上述的符号表示)
24.2019年3月31日,农业路大桥正式建成通车,大桥由梁、斜拉索和塔柱三部分组成,塔柱高150米;桥面为双向10车道;共设36对72根斜拉索,具有塔柱高、桥面宽、斜拉索索力大等特点;
(1)“塔柱为什么要造这么高?”科学兴趣小组的同学对此进行了研究:他们将大桥的结构进行简化,抽象成图1中甲的模型,又画了塔柱高低不同的两幅图乙和丙;可以看出它用到了杠杆的相关知识,其中O是支点,______代表桥重和过往车辆等产生的对桥的作用力;同学们通过比较发现:适当增加塔柱的高度,可______(选填“增大”或“减小”)斜拉索拉力的力臂,从而减轻斜拉索承受的拉力;
(2)大桥在历经四年修建过程中常用到如图2中甲所示的起重机,若起重器吊臂前端是由如图2中乙所示的滑轮组组成,动滑轮质量为100kg,绳重和摩擦不计;如果拉力的功率为6kW,则把2×103kg的货物匀速提高10m;(g取10N/kg)求:
①拉力F的大小是多少?______
②这一过程需要多长时间?______
③滑轮组机械效率是多少?______
25.(1)图中的弹簧测力计的示数是______N;
(2)图中物体的长度是______cm;
(3)请画出图中重20N的小球所受重力的示意图;( )
(4)请画出图中拉力F的力臂L。( )
26.2019年10月10日18时10分许,江苏省无锡市312国道K135处,锡港路上跨桥发生桥面侧翻事故,致3人死亡,2人受伤,经查事故原因是运输车辆超载并且在外车道行驶所致。据报道,超载车辆总重184t相当于4.5架我国自主研发的C919飞机空载时起飞的重量。如图甲事故现场的独柱桥墩只有一个支撑。为了研究超载问题,小明做了一套实验装置如图乙所示,将长1.2m,重36N的均质木棒平放在水平方形台面上,B、C为与台面的接触点,A、D分别为左右两端点,它们距台面边缘处的距离均为AB=CD=0.4m。在A端挂一个重为G1=30N的物体,在D端挂一个重为G2的物体。
①若G2=30N,台面受到木棒的压力为_______N。
②若D端挂物体后,木棒仍在水平台面上静止,则D端所挂物体的力G2的最小值为_______N,最大值为_______N。
③若D端不挂重物,则物体G1可以挂到距离B点左端的最大距离是_______cm处,木棒仍在水平台面上保持静止;由此小明猜想如果当时运输车沿大桥_______(选填“外”或“内”)侧车道行驶,悲剧可能就不会发生。
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【详解】
定滑轮是一个等臂杠杆,不能省力,但可以改变力的方向,故ABD错误,C正确。
故选C。
2.C
【详解】
当在水平方向使用动滑轮时,拉力所要克服的是摩擦力。绳子对A的拉力就等于A所受到的摩擦力,作用在动滑轮上的绳子有2段,则
得
故ABD不符合题意,C符合题意。
故选C。
3.D
忽略绳重及摩擦,克服物体重力所做的功为有用功,克服物体和动滑轮重力所做的功为总功,根据η=×100%=×100%=×100%进行解答.
【详解】
忽略绳重及摩擦,滑轮组的机械效率为:
η=×100%=×100%=×100%=×100%
A. 由表达式可知,滑轮组的机械效率与物体被提升的高度无关,故A错误;
B. 由表达式可知, 增大动滑轮的重力G动,变大,滑轮组的机械效率变小,故B错误;
C. 由表达式可知,滑轮组的机械效率与承担重物的绳子的段数无关,故C错误;
D. 由表达式可知,增加物体的重力G,变小,滑轮组的机械效率变大,故D正确.
故选D.
4.D
【详解】
A.“标”“本”表示力臂,“权”“重”表示力,故A错误;
B.杠杆绕着O转动,故O为支点,故B错误;
C.“权”小于“重”时,端可能上扬,因为杠杆平衡原理可知,平衡不仅与力有关还与力臂有关,故C错误;
D.增大“重”时,重与OB的乘积变大,在权不变的情况下可以增大标,故应把“权”向端移,故D正确。
故选D。
5.D
【详解】
A.由图丙可知,在1~2s内(第2s内)A被匀速提升,由图乙可知拉力F=20N,由图知,n=2,忽略绳重及摩擦,动滑轮重力
G动=2F-GA=2×20N-25N=15N
故A正确,不符合题意;
B.由图丙可知,第2s内A上升的速度vA=2m/s,第2s内滑轮上升的高度
h=vAt=2m/s×1s=2m
第2秒内克服滑轮重做的额外功为
W额=G动h=15N×2m=30J
故B正确,不符合题意;
C.忽略绳重及摩擦,绳子拉力
G =2F最大-GA-G动=2×100N-25N-15N=160N
故C正确,不符合题意;
D.此装置提升重物的机械效率随提升物重的增大而增大,此装置提升重物的最大机械效率
故D错误,符合题意。
故选D。
6.A
【详解】
A.滑轮组的机械效率为
故A选项正确;
B.动滑轮重力大小
因为不可忽略绳重和机械部件间的摩擦,故动滑轮重力大小一定不是90N,故B选项错误;
C.绳子自由端移动的距离是重物移动距离的3倍,为6m,故C选项错误;
D.提升物体的过程中,拉力F功率为
故D选项错误。
故选A。
7.C
【详解】
A.由图知,使杠杆逆时针转动的力是物体对杠杆的拉力,故A错误;
BC.杠杆在A位置(如下图)
LOA=2LOC
拉力
因为拉力
F<G
所以此杠杆为省力杠杆,故B错误,C正确;
D.如下图所示
杠杆在B位置,OA′为动力臂,OC′为阻力臂,阻力不变为G,因为
△OC′D∽△OA′B
所以
OC′∶OA′=OD∶OB=1∶2
因为杠杆平衡,所以
F′LOA′=GLOC′
由此可知,当杠杆从A位置匀速提到B位置的过程中,力F的大小不变,故D错误。
故选C。
8.C
【详解】
A.自行车的脚踏装置,是轮轴,动力臂大于阻力臂,根据杠杆平衡,动力小于阻力,是省力杠杆,故A不符合题意;
B.盘山公路是斜面,省力费距离,故B不符合题意;
C.划船用的浆,是阻力臂大于动力臂,阻力小于动力,是费力杠杆,费力,但是省了距离,故C符合题意;
D.道钉撬动力臂大于阻力臂,是省力杠杆,费距离,故D不符合题意。
故选C。
9.B
根据滑轮组可知,本题考查有关于滑轮组的机械效率综合计算,根据滑轮组的特点及机械效率的计算公式进行求解.
【详解】
由图可知,n=2
A.不计绳重和轮与轴的摩擦,则绳子自由端受到的拉力:
故A错误.
BC.有用功:
故C错误;
额外功:
总功:
滑轮组的机械效率:
故B正确.
D.拉力F做功的功率:
故D错误.
10.D
【详解】
F1和F2使杠杆转动的方向与重物、杠杆转动的方向相反,可以使杠杆平衡;而F3的力臂为零,不能使杠杆平衡;F4使杠杆转动的方向与重物、杠杆转动方向相同,不能使杠杆平衡。故ABC不符合题意,D符合题意。
故选D。
11.C
【详解】
A.机械做功越快,功率越大,机械效率是有用功占总功的比例,做功的快慢与机械效率无关,故A错误;
B.机械做功越多,不清楚是有用功和总功的占比,故机械效率未知,故B错误;
CD.使用机械可以省力或省距离,但不能省功,任何机械都不能省功,故C正确;故D错误。
故选C。
12.D
【详解】
A.甲、乙图绳子的有效段数(n)分别为3、2,甲滑轮组的机械效率为
①
乙滑轮组的机械效率为
②
若F甲=F乙且G甲=G乙,乙的机械效率大于甲的机械效率,故A不符合题意;
B.由①②知,机械效率与提升物体的高度无关,若F甲=F乙,根据①②,因不知G甲与G乙的大小关系,故无法确定甲、乙机械效率大小,故B不符合题意;
C.不计绳重及摩擦,则克服动滑轮的重力做的功为额外功的唯一来源,因总功等于有用功与额外功之和,故甲、乙滑轮组的机械效率为
③
若G甲=G乙且滑轮重均相同,可知甲、乙的机械效率相同,故C不符合题意;
D.甲、乙图绳子的有效段数(n)分别为3、2。不计绳重及摩擦,则作用在绳子自由端的拉力为
则提升物体的重力为
G=nF-G动
若F甲=F乙且滑轮重均相同,则可知,甲滑轮组提升物体的重力较大,根据③式有
故可知甲的机械效率比乙高,故乙的机械效率比较低,故D符合题意。
故选D。
13.C
【详解】
因铅球和铜球体积相同,ρ铅>ρ铜,由m=ρV可知,m铅>m铜,则
G铅>G铜
由杠杆平衡条件可知
G铅×L1=G铜×L2
并且
L1<L2
将两球同时浸没在水中,由F浮=ρ水gV排可知,两球受到的浮力相等;由杠杆平衡条件可得,左边
(G铅﹣F浮)L1=G铅×L1﹣F浮L1
右边
(G铜﹣F浮)L2=G铜×L2﹣F浮L2
因为L1<L2,所以
G铅×L1﹣F浮L1>G铜×L2﹣F浮L2
故左端下沉,即杠杆逆时针转动,故C选项正确。
故选C。
14.D
【详解】
A.因为不计滑轮重、绳重和滑轮摩擦,拉力F=16N,根据动滑轮的特点可知,每段绳子上的力为8N。又因为弹簧测力计的示数为2N,物体B相对于地面静止,所以物体B与木板A之间的摩擦力为2N。木板受到向右的绳子拉力等于地面的摩擦力加上B的摩擦力,所以地面对木板A的摩擦力是
fA=8N-2N=6N
故A错误;
B.木板A的移动速度为0.3m/s,动滑轮的移动速度等于拉力F的移动速度,等于木板移动速度的二分之一,大小为0.15m/s,故B错误;
C.物块B始终静止,由力的平衡条件可得,物块B受到的摩擦力等于弹簧测力计的示数为2N,方向水平向右,故C错误;
D.绳子拉木板的功率是
故D正确。
故选D。
15.D
【详解】
A.由图可知承重绳子股数n=2,因为忽略绳重、摩擦、空气阻力时所需拉力
所以动滑轮的重力
故A正确,不符合题意;
B.由可知,A移动的距离等于动滑轮移动的距离
所以克服滑轮重做的额外功
故B正确,不符合题意;
C.因为忽略绳重、摩擦、空气阻力时
所以货物的最大重力
故C正确,不符合题意;
D.因为此装置提升重物的机械效率随提升物重的增大而增大,所以此装置运载货物的最高机械效率
故D错误,D符合题意。
故选D。
16. 230 200 57.5
【详解】
[1]一共有两段绳子分担动滑轮的重力,故人需用的拉力为
[2]人所做的有用功为
[3]拉力做功的功率为
17. 0.4 20
【详解】
[1]由图可知,n=2,vA=0.2m/s,则物体B下滑的速度为
vB=2vA=2×0.2m/s=0.4m/s
[2]物体B匀速下降,则绳端的拉力
F拉=GB=10N
不计摩擦、绳重及滑轮重
F拉=f
物体A与水平面间的摩擦力
f=2F拉=2×10N=20N
18. 240 24 83.3% 20
【详解】
[1]对木箱施加平行于斜面的大小为120N的拉力,斜面长为2m,此过程中拉力做功
W总=FS=120N×2m=240J
[2]将其以0.2m/s的速度匀速拉到顶端,拉力的功率
[3]使用斜面做的有用功
W有用=Gh=200N×1m=200J
斜面的机械效率
[4]因为W总=W有用+W额,所以克服摩擦力做的额外功
W额=W总-W有用=240J-200J=40J
由W额=fs得摩擦力大小
19. 费力 等于 80%
【详解】
(1)[1]根据表格数据可知
F甲>GM,F乙<GM
所以使用甲提升物体M时费力。
[2]将同一物体M匀速提升同样高度,由
W有=Gh
可知,甲乙机械做的有用功相等。
(2)[3]由图乙可知,滑轮组的动滑轮绕2段绳子,乙提升物体M时的机械效率
20. L1L4=L2L3
【详解】
[1]若物体W放在平台上的某一位置时,刀口A和E的受力相等,设物体W的质量为M0,按题意可得
FA=FE=0.5×(M+M0)g ①
以P点为支点,根据杠杆的平衡条件有
mgL4=F0L5 ②
以B点为支点,根据杠杆的平衡条件有
F0(L5+L4+L2)=FAL1 +FCFL2 ③
以D点为支点,根据杠杆的平衡条件有
FCFL4 =FEL3 ④
联立以上四式可得
[2]设物体重心与刀口A的距离为x,以E为支点,根据杠杆的平衡条件有
故
④
以A为支点,根据杠杆的平衡条件有
故
⑤
联立②③④⑤式可得
因此与x无关的条件是
L2L3L5-L1L4L5=0
即
L1L4=L2L3
21. 费力 动力臂小于阻力臂
【详解】
(1)[1]从支点O向力F2的作用线做出垂线段,垂线段的长度为F2的力臂l2,如图所示:
(2)[2]阻力和阻力臂不变,动力臂越长越省力,由图知最长的动力臂为支点O与作用点B的连线,然后根据力臂的画法作出垂直于力臂OB的作用力F1即可,为使杠杆平衡,动力的方向应垂直于OB向上。如图所示:
(3)[3][4]由图可知动力臂小于阻力臂,此杠杆是费力杠杆。
22. 0.5kg 1.1kg 偏大
【详解】
解:(1)[1]杆秤能够绕O点转动,可以看成是一个杠杆,秤杆水平静止时,秤砣的重力对应的力臂是OB,被称量物体重力对应的力臂是OA,根据杠杆平衡条件有
即
代入数据可得被测物体的质量
(2)[2]若秤杆长60cm,不改变OA的长度,要求称量物体质量最大,根据杠杆平衡条件可知,秤砣重力对应力臂应该最长,即为
L=60cm-5cm=55cm
假设最大称量质量为M,则根据杠杆平衡条件有
则
(3)[3]若秤砣有缺损,秤砣质量减小,而被称量物体重力和对应的力臂不变,根据杠杆平衡条件可知OB的长度要变大,即杆秤所示的质量会偏大。
答:(1)被测物体的质量是0.5kg;
(2)若秤杆长60cm,不改变OA的长度,则这把秤最大能称量1.1kg千克的物体;
(3)若秤砣有缺损时,则杆秤所示的质量会比真实值偏大。
23. 甲
【详解】
(1)[1]过支点O作垂直于力F1的作用线的垂线段,即力臂L1,如下图
(2)[2]由甲图知道,重力的力臂小于拉力的力臂,由杠杆的平衡条件知道,拉力大于重力,即提升物体M时会费力;乙图中使用的是定滑轮,既不也不费力;由功的原理知道,使用斜面可以省力。
(3)[3]根据题意知道,F3对物体做的功为W3是总功,F4对物体所做的功为W4是有用功,由知道,则该斜面的机械效率
24. F1 增大 7000N 35s 95.2%
【详解】
(1)[1]由抽象成的模型图可知,它用到的杠杆的相关知识,图中F0为拉索的拉力,F1相当于桥重和过往车辆等产生的对桥的作用力,O点此杠杆的支点。
[2]如下图所示,桥塔高度增加后,阻力F1及其力臂不变,L0'>L0,即动力臂增大,由杠杆的平衡条件可知:斜拉索的拉力F0减小。
(2)①[3]由图知,n=3,拉力端移动距离
s=3h=3×10m=30m
绳重和摩擦不计,拉力
F=(G+G轮)=× (2×103kg×10N/kg+100kg×10N/kg)=7000N
②[4]拉力做功
W=Fs=7000N×30m=2.1×105J
由P=得做功时间
t===35s
③[5]有用功
W有用=Gh=2×104N×10m=2×105J
滑轮组的机械效率
η=×100%=×100%≈95.2%
25. 3.6 2.88
【详解】
(1)[1]由图可知,弹簧测力计的分度值为0.2N,故弹簧测力计的示数为3.6N。
(2)[2]由图可知,刻度尺的分度值是0.1cm,物体的长度为2.88cm。
(3)[3]重力的作用点在重心,重心就是小球重心,方向竖直向下,过小球中心沿着竖直向下的方向做带有箭头的线段即为重力的示意图,如图所示:
(4)[4]从支点向力的作用线做垂线,垂线段即为力臂,如图所示:
26. 96 6 78 24 内
【详解】
①[1]放在水平方形台面上的木棒受左右两物体的竖直向下的拉力、重力和台面竖直向上的支持力,即
F支持=F拉+G木棒=2G+G木棒=2×30N+36N=96N
因为木棒对台面的压力和台面对木棒的支持力是相互作用力,大小相等,即
F压力=F支持=96N
②[2][3]若以右边缘C为支点,右边力臂最小,力最大,木棒重心在中点处,重力力臂为0.2m,G2力臂为0.4m,G1力臂为
1.2m-0.4m=0.8m
根据杠杆的平衡条件可得
30N×0.8m+36N×0.2m=G2×0.4m
解得
G2最大=78N
若以左边缘B为支点,右边力臂最大,力最小,同理,根据杠杆平衡条件可得
30N×0.4m=36N×0.2m+G2×0.8m
解得
G2=6N
③[4][5]若D端不挂重物,则支点在B点,木棒仍在水平台面上保持静止,根据杠杆的平衡条件可得
G1×L1=G木棒×L2
即
30N×L=36N×0.2m
解得
L=0.24m=24cm
即物体G1可以挂到距离B点左端的最大距离是24cm。由此小明猜想如果当时运输车沿大桥内侧车道行驶,悲剧可能就不会发生。
答案第1页,共2页
答案第1页,共2页
一、单选题
1.下列关于定滑轮的说法正确的是( )
A.使用定滑轮可以省距离 B.使用定滑轮可以省力
C.使用定滑轮可以改变拉力方向 D.使用定滑轮可以省功
2.在图中,物体A的重力为G,在拉力F的作用下,物体沿水平桌面做匀速直线运动,已知物体受到的摩擦力为f,则人对绳的拉力F的大小等于( )
A.0.5G B.2G C.0.5f D.2f
3.用如图所示的滑轮组提升重物时(忽略绳重及摩擦),下列做法能提高滑轮组机械效率的有
A.增加物体被提升的高度
B.增大动滑轮的重力
C.改变绳子的绕法,减少承担重物的绳子的段数
D.增加物体的重力
4.如图所示,是我国古代《墨经》最早记述了秤的杠杆原理,有关它的说法正确的是( )
A.“标”“本”表示力,“权”“重”表示力臂
B.图中的点为杠杆的支点
C.“权”小于“重”时,端一定上扬
D.增大“重”时,应把“权”向端移
5.甲装置中,空吊篮A重25N,绳子承受最大拉力100N。小壮将A提升到高处,施加拉力F随时间变化关系如图乙,A上升速度随时间变化关系如图内。忽略绳重、摩擦、空气阻力。下列说法不正确的是( )
A.动滑轮所受的重力为15N
B.第2秒内克服滑轮重做的额外功为30J
C.此装置最多能匀速运载160N重的货物
D.此装置运载货物最高机械效率为92.5%
6.利用如图所示的滑轮组提起一个重为210N的物体,绳子自由端的拉力。5s内物体被匀速提升2m。不可忽略绳重和机械部件间的摩擦,则下列说法中正确的是( )
A.滑轮组的机械效率为70% B.动滑轮重力大小为90N
C.绳子自由端移动的距离是0.67m D.提升物体的过程中,拉力F功率为40W
7.如图,轻质杠杆OA中点通过细线悬挂一个重力为60N的物体,在A端施加一竖直向上的力F,杠杆在水平位置平衡,下列有关说法正确的是( )
A.使杠杆逆时针转动的力是物体的重力
B.此杠杆为费力杠杆
C.杠杆处于水平位置平衡时拉力F的大小为30N
D.保持F的方向竖直向上不变,将杠杆从A位置匀速提升到B位置的过程中,力F将增大
8.下列机械中,使用时不能省力但能省距离的是( )
A. 自行车的脚踏装置
B. 盘山公路
C. 划船用的浆
D. 道钉撬
9.如图所示,小明用滑轮组提升物体A,物体A重7N,定滑轮重2N,动滑轮重1N.物体A在1s内沿竖直方向匀速升高了0.2m.不计绳重和轮与轴的摩擦,下列说法中正确的是
A.绳子自由端受到的拉力大小是 3N
B.滑轮组的机械效率为 87.5%
C.有用功为 1.6J
D.拉力 F 做功的功率为 0.8W
10.如图所示,轻质杠杆可绕支点O自由转动,作用在A点处的各个拉力中,不可能使杠杆水平平衡的是( )
A.F1和F2 B.F1和F4 C.F2和F3 D.F3和F4
11.在生产和生活中经常使用各种机械,关于机械,下列说法正确的是( )
A.机械做功越快,机械效率越高 B.机械做功越多,机械效率越高
C.使用机械可以省力或省距离,但不能省功 D.使用机械可以省力、省距离,也可以省功
12.用四个滑轮和两根相同的绳子组成如图所示的甲、乙两个滑轮组,用它们匀速提起货物,在绳自由端施加竖直的拉力分别为F甲和F乙,物重分别为G甲和G乙,物体被提升高度分别为h甲、h乙,不计绳重及摩擦,则( )
A.若F甲=F乙且G甲=G乙,则乙的机械效率比较低
B.若F甲=F乙且h甲=h乙,则甲的机械效率比较低
C.若G甲=G乙且滑轮重均相同,则甲的机械效率比较低
D.若F甲=F乙且滑轮重均相同,则乙的机械效率比较低
13.在杠杆两端各悬挂一个体积相同的铅球和铜球处于平衡状态,现将两球同时浸没在水中(如图所示),则杠杆(ρ铅>ρ铜)( )
A.静止不动 B.顺时针转动
C.逆时针转动 D.支点受到的压力变大
14.如图所示,木板A放在一水平面上,用16N的水平拉力F拉滑轮,使足够长的木板A以0.3m/s的速度在水平地面上匀速运动,物体B相对于地面静止,弹簧测力计示数为2N,若不计滑轮重、弹簧测力计重、绳重和滑轮摩擦,则下列说法正确的是( )
A.木板A与地面的摩擦力为2N
B.滑轮向右移动的速度为0.3m/s
C.物块B受到的摩擦力为2N,方向水平向左
D.绳子拉木板的功率为2.4W
15.空吊篮A重25N,绳子承受最大拉力100N。小壮用20N的力以2m/s的速度将A匀速提升到高处,忽略绳重、摩擦、空气阻力。下列说法不正确的是( )
A.动滑轮所受的重力为15N
B.第2秒内克服滑轮重做的额外功为30J
C.此装置最多能匀速运载160N重的货物
D.此装置运载货物最高机械效率为92.5%
二、填空题
16.如图所示,人向下拉绳提升重物,已知物体重400N,动滑轮重60N,不计绳重及摩擦,将重物匀速提升0.5m用时4s,人需用的拉力为 _____N,人所做的有用功为 _____J,拉力做功的功率为 _____W。
17.如图所示,物体A重100N,物体B重10N,此时A沿着水平桌面以0.2m/s的速度向右做匀速直线运动(不计摩擦、绳重及滑轮重),那么物体B匀速下降的速度是___________m/s,物体A与水平面间的摩擦力是___________N。
18.小明为了把水平地面上重为200N的木箱移到1m高的平台上,搭建了长为2m斜面。如图所示,现对木箱施加平行于斜面的大小为120N的拉力,将其由底端以0.2m/s的速度匀速拉到顶端。在此过程中拉力做功______J,拉力的功率为______W,斜面的机械效率为______,摩擦力大小为______N。
19.如图所示,小明分别使用甲、乙图中两种不同的机械将同一物体M匀速提升同样高度。测得两次拉力F甲、F乙和物体M所受的重力G如下表所示。当使用乙机械时,测得绳子自由端移动的距离是物体M上升高度的2倍。
(1)从表中数据可知:甲机械________(选填“省力”“费力”或“不省力也不费力”),甲机械所做的有用功_______(选填“大于”“等于”或“小于”)乙机械所做的有用功:
(2)乙提升物体M时的机械效率是________
F甲 F乙 GM
10N 5N 8N
20.如图所示为某磅秤的结构示意图,物体W放在平台上,物体以及平台的重量由刀口A和E分担,并通过由DF、FC、BG、GO、OQ等轻质硬杆组成的杠杆组(自重不计)的作用由Q处悬挂的砝码表示出来。该秤的结构装置中B和D也为刀口,O、G、C、F处为光滑铰链,P为OQ杆的固定转动轴,P、D同在一竖直线上,Q、C、F同在另一竖直线上。已知:AB=L1,BC=L2,DE=L3,DF=L4,OP=L5。若物体W放在平台上的某一位置时,刀口A和E的受力相等,此时砝码的质量为m,T型平台的质量为M,则物体W的质量为______,若物体W不论放在平台上什么位置,秤的示数不变,则L1、L2、L3、L4之间应有的关系为______。
三、综合题
21.质量忽略不计的AC硬棒能绕O点转动,在C点挂一物体,在B点施加动力F时,棒刚好处于静止状态。
(1)画出F2的力臂______;
(2)在B点画出作用在杠杆上最小的动力F1;______
(3)此杠杆是______杠杆。(填:“省力”、“费力”或“等臂”)
判断依据是:______。
22.如图所示,一把杆秤不计自重,秤砣的质量为100g,秤杆水平静止时,OA=5cm, OB=25cm。求∶
(1)被测物体的质量;( )
(2)若秤杆长60cm,不改变OA的长度,则这把秤最大能称量多少千克的物体?( )
(3)若秤砣有缺损时,则杆秤所示的质量会比真实值______(“偏大”或“偏小”)。
23.如图所示,小明分别使用甲、乙、丙三种机械匀速提升物体M(绳长不变),测得拉力和物体M所受的重力如表所示,
(1)在甲图中,作出F1的力臂L1___________。
(2)三种机械中,提升物体M时会费力的有___________(选填“甲”、“乙”、“丙”)
(3)如图所示,丙图中,物体在F3的作用下,沿斜面匀速运动了s,F3对物体做的功为W3;丁图中,物体在F4的作用下,匀速提升至相同高度h时,F4对物体所做的功为W4;戊图中,物体在F5的作用下,在与斜面粗糙程度相同的水平面上,匀速直线运动了,F5对物体所做的功为W5,则该斜面的机械效率___________。(利用上述的符号表示)
24.2019年3月31日,农业路大桥正式建成通车,大桥由梁、斜拉索和塔柱三部分组成,塔柱高150米;桥面为双向10车道;共设36对72根斜拉索,具有塔柱高、桥面宽、斜拉索索力大等特点;
(1)“塔柱为什么要造这么高?”科学兴趣小组的同学对此进行了研究:他们将大桥的结构进行简化,抽象成图1中甲的模型,又画了塔柱高低不同的两幅图乙和丙;可以看出它用到了杠杆的相关知识,其中O是支点,______代表桥重和过往车辆等产生的对桥的作用力;同学们通过比较发现:适当增加塔柱的高度,可______(选填“增大”或“减小”)斜拉索拉力的力臂,从而减轻斜拉索承受的拉力;
(2)大桥在历经四年修建过程中常用到如图2中甲所示的起重机,若起重器吊臂前端是由如图2中乙所示的滑轮组组成,动滑轮质量为100kg,绳重和摩擦不计;如果拉力的功率为6kW,则把2×103kg的货物匀速提高10m;(g取10N/kg)求:
①拉力F的大小是多少?______
②这一过程需要多长时间?______
③滑轮组机械效率是多少?______
25.(1)图中的弹簧测力计的示数是______N;
(2)图中物体的长度是______cm;
(3)请画出图中重20N的小球所受重力的示意图;( )
(4)请画出图中拉力F的力臂L。( )
26.2019年10月10日18时10分许,江苏省无锡市312国道K135处,锡港路上跨桥发生桥面侧翻事故,致3人死亡,2人受伤,经查事故原因是运输车辆超载并且在外车道行驶所致。据报道,超载车辆总重184t相当于4.5架我国自主研发的C919飞机空载时起飞的重量。如图甲事故现场的独柱桥墩只有一个支撑。为了研究超载问题,小明做了一套实验装置如图乙所示,将长1.2m,重36N的均质木棒平放在水平方形台面上,B、C为与台面的接触点,A、D分别为左右两端点,它们距台面边缘处的距离均为AB=CD=0.4m。在A端挂一个重为G1=30N的物体,在D端挂一个重为G2的物体。
①若G2=30N,台面受到木棒的压力为_______N。
②若D端挂物体后,木棒仍在水平台面上静止,则D端所挂物体的力G2的最小值为_______N,最大值为_______N。
③若D端不挂重物,则物体G1可以挂到距离B点左端的最大距离是_______cm处,木棒仍在水平台面上保持静止;由此小明猜想如果当时运输车沿大桥_______(选填“外”或“内”)侧车道行驶,悲剧可能就不会发生。
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【详解】
定滑轮是一个等臂杠杆,不能省力,但可以改变力的方向,故ABD错误,C正确。
故选C。
2.C
【详解】
当在水平方向使用动滑轮时,拉力所要克服的是摩擦力。绳子对A的拉力就等于A所受到的摩擦力,作用在动滑轮上的绳子有2段,则
得
故ABD不符合题意,C符合题意。
故选C。
3.D
忽略绳重及摩擦,克服物体重力所做的功为有用功,克服物体和动滑轮重力所做的功为总功,根据η=×100%=×100%=×100%进行解答.
【详解】
忽略绳重及摩擦,滑轮组的机械效率为:
η=×100%=×100%=×100%=×100%
A. 由表达式可知,滑轮组的机械效率与物体被提升的高度无关,故A错误;
B. 由表达式可知, 增大动滑轮的重力G动,变大,滑轮组的机械效率变小,故B错误;
C. 由表达式可知,滑轮组的机械效率与承担重物的绳子的段数无关,故C错误;
D. 由表达式可知,增加物体的重力G,变小,滑轮组的机械效率变大,故D正确.
故选D.
4.D
【详解】
A.“标”“本”表示力臂,“权”“重”表示力,故A错误;
B.杠杆绕着O转动,故O为支点,故B错误;
C.“权”小于“重”时,端可能上扬,因为杠杆平衡原理可知,平衡不仅与力有关还与力臂有关,故C错误;
D.增大“重”时,重与OB的乘积变大,在权不变的情况下可以增大标,故应把“权”向端移,故D正确。
故选D。
5.D
【详解】
A.由图丙可知,在1~2s内(第2s内)A被匀速提升,由图乙可知拉力F=20N,由图知,n=2,忽略绳重及摩擦,动滑轮重力
G动=2F-GA=2×20N-25N=15N
故A正确,不符合题意;
B.由图丙可知,第2s内A上升的速度vA=2m/s,第2s内滑轮上升的高度
h=vAt=2m/s×1s=2m
第2秒内克服滑轮重做的额外功为
W额=G动h=15N×2m=30J
故B正确,不符合题意;
C.忽略绳重及摩擦,绳子拉力
G =2F最大-GA-G动=2×100N-25N-15N=160N
故C正确,不符合题意;
D.此装置提升重物的机械效率随提升物重的增大而增大,此装置提升重物的最大机械效率
故D错误,符合题意。
故选D。
6.A
【详解】
A.滑轮组的机械效率为
故A选项正确;
B.动滑轮重力大小
因为不可忽略绳重和机械部件间的摩擦,故动滑轮重力大小一定不是90N,故B选项错误;
C.绳子自由端移动的距离是重物移动距离的3倍,为6m,故C选项错误;
D.提升物体的过程中,拉力F功率为
故D选项错误。
故选A。
7.C
【详解】
A.由图知,使杠杆逆时针转动的力是物体对杠杆的拉力,故A错误;
BC.杠杆在A位置(如下图)
LOA=2LOC
拉力
因为拉力
F<G
所以此杠杆为省力杠杆,故B错误,C正确;
D.如下图所示
杠杆在B位置,OA′为动力臂,OC′为阻力臂,阻力不变为G,因为
△OC′D∽△OA′B
所以
OC′∶OA′=OD∶OB=1∶2
因为杠杆平衡,所以
F′LOA′=GLOC′
由此可知,当杠杆从A位置匀速提到B位置的过程中,力F的大小不变,故D错误。
故选C。
8.C
【详解】
A.自行车的脚踏装置,是轮轴,动力臂大于阻力臂,根据杠杆平衡,动力小于阻力,是省力杠杆,故A不符合题意;
B.盘山公路是斜面,省力费距离,故B不符合题意;
C.划船用的浆,是阻力臂大于动力臂,阻力小于动力,是费力杠杆,费力,但是省了距离,故C符合题意;
D.道钉撬动力臂大于阻力臂,是省力杠杆,费距离,故D不符合题意。
故选C。
9.B
根据滑轮组可知,本题考查有关于滑轮组的机械效率综合计算,根据滑轮组的特点及机械效率的计算公式进行求解.
【详解】
由图可知,n=2
A.不计绳重和轮与轴的摩擦,则绳子自由端受到的拉力:
故A错误.
BC.有用功:
故C错误;
额外功:
总功:
滑轮组的机械效率:
故B正确.
D.拉力F做功的功率:
故D错误.
10.D
【详解】
F1和F2使杠杆转动的方向与重物、杠杆转动的方向相反,可以使杠杆平衡;而F3的力臂为零,不能使杠杆平衡;F4使杠杆转动的方向与重物、杠杆转动方向相同,不能使杠杆平衡。故ABC不符合题意,D符合题意。
故选D。
11.C
【详解】
A.机械做功越快,功率越大,机械效率是有用功占总功的比例,做功的快慢与机械效率无关,故A错误;
B.机械做功越多,不清楚是有用功和总功的占比,故机械效率未知,故B错误;
CD.使用机械可以省力或省距离,但不能省功,任何机械都不能省功,故C正确;故D错误。
故选C。
12.D
【详解】
A.甲、乙图绳子的有效段数(n)分别为3、2,甲滑轮组的机械效率为
①
乙滑轮组的机械效率为
②
若F甲=F乙且G甲=G乙,乙的机械效率大于甲的机械效率,故A不符合题意;
B.由①②知,机械效率与提升物体的高度无关,若F甲=F乙,根据①②,因不知G甲与G乙的大小关系,故无法确定甲、乙机械效率大小,故B不符合题意;
C.不计绳重及摩擦,则克服动滑轮的重力做的功为额外功的唯一来源,因总功等于有用功与额外功之和,故甲、乙滑轮组的机械效率为
③
若G甲=G乙且滑轮重均相同,可知甲、乙的机械效率相同,故C不符合题意;
D.甲、乙图绳子的有效段数(n)分别为3、2。不计绳重及摩擦,则作用在绳子自由端的拉力为
则提升物体的重力为
G=nF-G动
若F甲=F乙且滑轮重均相同,则可知,甲滑轮组提升物体的重力较大,根据③式有
故可知甲的机械效率比乙高,故乙的机械效率比较低,故D符合题意。
故选D。
13.C
【详解】
因铅球和铜球体积相同,ρ铅>ρ铜,由m=ρV可知,m铅>m铜,则
G铅>G铜
由杠杆平衡条件可知
G铅×L1=G铜×L2
并且
L1<L2
将两球同时浸没在水中,由F浮=ρ水gV排可知,两球受到的浮力相等;由杠杆平衡条件可得,左边
(G铅﹣F浮)L1=G铅×L1﹣F浮L1
右边
(G铜﹣F浮)L2=G铜×L2﹣F浮L2
因为L1<L2,所以
G铅×L1﹣F浮L1>G铜×L2﹣F浮L2
故左端下沉,即杠杆逆时针转动,故C选项正确。
故选C。
14.D
【详解】
A.因为不计滑轮重、绳重和滑轮摩擦,拉力F=16N,根据动滑轮的特点可知,每段绳子上的力为8N。又因为弹簧测力计的示数为2N,物体B相对于地面静止,所以物体B与木板A之间的摩擦力为2N。木板受到向右的绳子拉力等于地面的摩擦力加上B的摩擦力,所以地面对木板A的摩擦力是
fA=8N-2N=6N
故A错误;
B.木板A的移动速度为0.3m/s,动滑轮的移动速度等于拉力F的移动速度,等于木板移动速度的二分之一,大小为0.15m/s,故B错误;
C.物块B始终静止,由力的平衡条件可得,物块B受到的摩擦力等于弹簧测力计的示数为2N,方向水平向右,故C错误;
D.绳子拉木板的功率是
故D正确。
故选D。
15.D
【详解】
A.由图可知承重绳子股数n=2,因为忽略绳重、摩擦、空气阻力时所需拉力
所以动滑轮的重力
故A正确,不符合题意;
B.由可知,A移动的距离等于动滑轮移动的距离
所以克服滑轮重做的额外功
故B正确,不符合题意;
C.因为忽略绳重、摩擦、空气阻力时
所以货物的最大重力
故C正确,不符合题意;
D.因为此装置提升重物的机械效率随提升物重的增大而增大,所以此装置运载货物的最高机械效率
故D错误,D符合题意。
故选D。
16. 230 200 57.5
【详解】
[1]一共有两段绳子分担动滑轮的重力,故人需用的拉力为
[2]人所做的有用功为
[3]拉力做功的功率为
17. 0.4 20
【详解】
[1]由图可知,n=2,vA=0.2m/s,则物体B下滑的速度为
vB=2vA=2×0.2m/s=0.4m/s
[2]物体B匀速下降,则绳端的拉力
F拉=GB=10N
不计摩擦、绳重及滑轮重
F拉=f
物体A与水平面间的摩擦力
f=2F拉=2×10N=20N
18. 240 24 83.3% 20
【详解】
[1]对木箱施加平行于斜面的大小为120N的拉力,斜面长为2m,此过程中拉力做功
W总=FS=120N×2m=240J
[2]将其以0.2m/s的速度匀速拉到顶端,拉力的功率
[3]使用斜面做的有用功
W有用=Gh=200N×1m=200J
斜面的机械效率
[4]因为W总=W有用+W额,所以克服摩擦力做的额外功
W额=W总-W有用=240J-200J=40J
由W额=fs得摩擦力大小
19. 费力 等于 80%
【详解】
(1)[1]根据表格数据可知
F甲>GM,F乙<GM
所以使用甲提升物体M时费力。
[2]将同一物体M匀速提升同样高度,由
W有=Gh
可知,甲乙机械做的有用功相等。
(2)[3]由图乙可知,滑轮组的动滑轮绕2段绳子,乙提升物体M时的机械效率
20. L1L4=L2L3
【详解】
[1]若物体W放在平台上的某一位置时,刀口A和E的受力相等,设物体W的质量为M0,按题意可得
FA=FE=0.5×(M+M0)g ①
以P点为支点,根据杠杆的平衡条件有
mgL4=F0L5 ②
以B点为支点,根据杠杆的平衡条件有
F0(L5+L4+L2)=FAL1 +FCFL2 ③
以D点为支点,根据杠杆的平衡条件有
FCFL4 =FEL3 ④
联立以上四式可得
[2]设物体重心与刀口A的距离为x,以E为支点,根据杠杆的平衡条件有
故
④
以A为支点,根据杠杆的平衡条件有
故
⑤
联立②③④⑤式可得
因此与x无关的条件是
L2L3L5-L1L4L5=0
即
L1L4=L2L3
21. 费力 动力臂小于阻力臂
【详解】
(1)[1]从支点O向力F2的作用线做出垂线段,垂线段的长度为F2的力臂l2,如图所示:
(2)[2]阻力和阻力臂不变,动力臂越长越省力,由图知最长的动力臂为支点O与作用点B的连线,然后根据力臂的画法作出垂直于力臂OB的作用力F1即可,为使杠杆平衡,动力的方向应垂直于OB向上。如图所示:
(3)[3][4]由图可知动力臂小于阻力臂,此杠杆是费力杠杆。
22. 0.5kg 1.1kg 偏大
【详解】
解:(1)[1]杆秤能够绕O点转动,可以看成是一个杠杆,秤杆水平静止时,秤砣的重力对应的力臂是OB,被称量物体重力对应的力臂是OA,根据杠杆平衡条件有
即
代入数据可得被测物体的质量
(2)[2]若秤杆长60cm,不改变OA的长度,要求称量物体质量最大,根据杠杆平衡条件可知,秤砣重力对应力臂应该最长,即为
L=60cm-5cm=55cm
假设最大称量质量为M,则根据杠杆平衡条件有
则
(3)[3]若秤砣有缺损,秤砣质量减小,而被称量物体重力和对应的力臂不变,根据杠杆平衡条件可知OB的长度要变大,即杆秤所示的质量会偏大。
答:(1)被测物体的质量是0.5kg;
(2)若秤杆长60cm,不改变OA的长度,则这把秤最大能称量1.1kg千克的物体;
(3)若秤砣有缺损时,则杆秤所示的质量会比真实值偏大。
23. 甲
【详解】
(1)[1]过支点O作垂直于力F1的作用线的垂线段,即力臂L1,如下图
(2)[2]由甲图知道,重力的力臂小于拉力的力臂,由杠杆的平衡条件知道,拉力大于重力,即提升物体M时会费力;乙图中使用的是定滑轮,既不也不费力;由功的原理知道,使用斜面可以省力。
(3)[3]根据题意知道,F3对物体做的功为W3是总功,F4对物体所做的功为W4是有用功,由知道,则该斜面的机械效率
24. F1 增大 7000N 35s 95.2%
【详解】
(1)[1]由抽象成的模型图可知,它用到的杠杆的相关知识,图中F0为拉索的拉力,F1相当于桥重和过往车辆等产生的对桥的作用力,O点此杠杆的支点。
[2]如下图所示,桥塔高度增加后,阻力F1及其力臂不变,L0'>L0,即动力臂增大,由杠杆的平衡条件可知:斜拉索的拉力F0减小。
(2)①[3]由图知,n=3,拉力端移动距离
s=3h=3×10m=30m
绳重和摩擦不计,拉力
F=(G+G轮)=× (2×103kg×10N/kg+100kg×10N/kg)=7000N
②[4]拉力做功
W=Fs=7000N×30m=2.1×105J
由P=得做功时间
t===35s
③[5]有用功
W有用=Gh=2×104N×10m=2×105J
滑轮组的机械效率
η=×100%=×100%≈95.2%
25. 3.6 2.88
【详解】
(1)[1]由图可知,弹簧测力计的分度值为0.2N,故弹簧测力计的示数为3.6N。
(2)[2]由图可知,刻度尺的分度值是0.1cm,物体的长度为2.88cm。
(3)[3]重力的作用点在重心,重心就是小球重心,方向竖直向下,过小球中心沿着竖直向下的方向做带有箭头的线段即为重力的示意图,如图所示:
(4)[4]从支点向力的作用线做垂线,垂线段即为力臂,如图所示:
26. 96 6 78 24 内
【详解】
①[1]放在水平方形台面上的木棒受左右两物体的竖直向下的拉力、重力和台面竖直向上的支持力,即
F支持=F拉+G木棒=2G+G木棒=2×30N+36N=96N
因为木棒对台面的压力和台面对木棒的支持力是相互作用力,大小相等,即
F压力=F支持=96N
②[2][3]若以右边缘C为支点,右边力臂最小,力最大,木棒重心在中点处,重力力臂为0.2m,G2力臂为0.4m,G1力臂为
1.2m-0.4m=0.8m
根据杠杆的平衡条件可得
30N×0.8m+36N×0.2m=G2×0.4m
解得
G2最大=78N
若以左边缘B为支点,右边力臂最大,力最小,同理,根据杠杆平衡条件可得
30N×0.4m=36N×0.2m+G2×0.8m
解得
G2=6N
③[4][5]若D端不挂重物,则支点在B点,木棒仍在水平台面上保持静止,根据杠杆的平衡条件可得
G1×L1=G木棒×L2
即
30N×L=36N×0.2m
解得
L=0.24m=24cm
即物体G1可以挂到距离B点左端的最大距离是24cm。由此小明猜想如果当时运输车沿大桥内侧车道行驶,悲剧可能就不会发生。
答案第1页,共2页
答案第1页,共2页
