【课件】5.5三角恒等变换5.5.1两角和与差的正弦、余弦和正切公式(课时2) 高中数学-RJA-必修第一册(共32张PPT)
文档属性
| 名称 | 【课件】5.5三角恒等变换5.5.1两角和与差的正弦、余弦和正切公式(课时2) 高中数学-RJA-必修第一册(共32张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-18 15:43:17 | ||
图片预览










文档简介
(共32张PPT)
数学-RJ·A-必修第一册
5.5 三角恒等变换
5.5.1 两角和与差的正弦、余弦和正切公式
第五章 三角函数
学习目标
1.经历用单位圆以及圆的旋转对称性推导出两角差的余弦公式的过程.
2.能从两角差的余弦公式导出两角和与差的正弦、余弦、正切公式,二倍角的正弦、余弦、正切公式,了解它们的内在联系.
3.会用两角和与差的正弦、余弦、正切公式以及二倍角公式进行简单的三角函数的化简、求值、证明.
重点:引导学生通过独立探究和讨论交流,导出两角和与差的三角函数的十一个公式,并了解它们的内在联系,为运用这些公式进行简单的恒等变换打好基础.
难点:两角差的余弦公式的探究.
知识梳理
推导:
sin(α+β)=sin αcos β+cos αsin β,当α=β时,sin 2α=2sin αcos α;
cos(α+β)=cos αcos β-sin αsin β,当α=β时,cos 2α=cos2 α-sin2 α ;
,当α=β时, .
二倍角的正弦、余弦、正切公式
利用S(α±β),C(α±β),T(α±β)推导出sin 2α,cos 2α,tan 2α的公式
课 时 2
通过推导,可以得到:
sin 2α=2sin αcos α, (S2α)
cos 2α=cos2α-sin2α, (C2α)
. (T2α)
如果要求二倍角的余弦公式(C2α)中仅含α的正弦(余弦),那么又可得到:
cos 2α=1-2sin2α, cos 2α=2cos2α-1.
以上这些公式都叫做倍角公式.倍角公式给出了α的三角函数与2α的三角函数之间的关系.(这里的“倍角”专指“二倍角”,遇到“三倍角”等名词时,“三”字等不可省去.)·
二倍角的“广义理解”:二倍角是相对的,如4α是2α的二倍,α是 的二倍等,“倍”是描述两个数量之间的关系的,这里蕴含着换元思想.
对于S2α和C2α,α∈R,但是在使用T2α时,要保证分母1-tan2α≠0且tan α有意义,即α≠kπ+ 且α≠kπ- 且α≠kπ+ (k∈Z).当α=kπ+ 及α=kπ- (k∈Z)时,tan 2α的值不存在;当α=kπ+ (k∈Z)时,tan α的值不存在,故不能用二倍角公式求tan 2α,此时可以利用诱导公式直接求tan 2α.
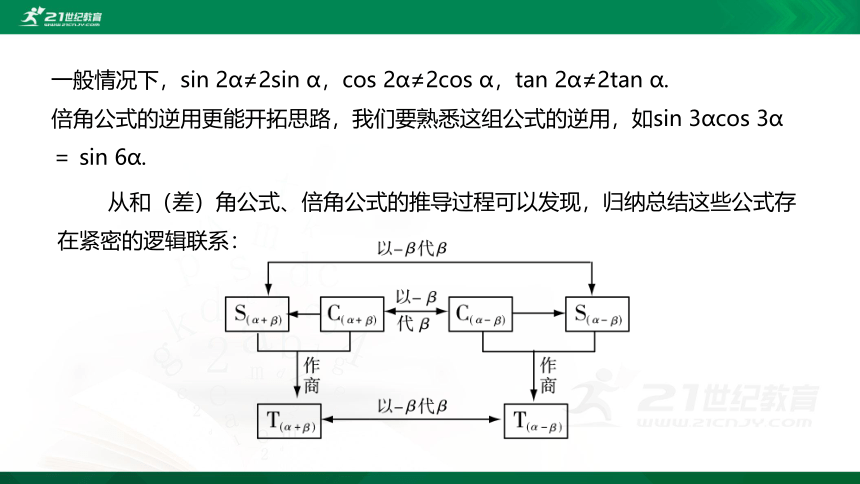
一般情况下,sin 2α≠2sin α,cos 2α≠2cos α,tan 2α≠2tan α.
倍角公式的逆用更能开拓思路,我们要熟悉这组公式的逆用,如sin 3αcos 3α= sin 6α.
从和(差)角公式、倍角公式的推导过程可以发现,归纳总结这些公式存在紧密的逻辑联系:
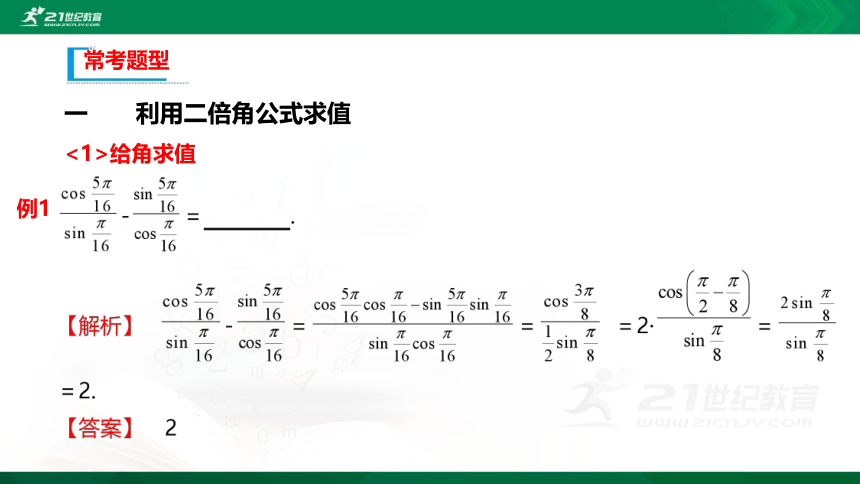
一 利用二倍角公式求值
<1>给角求值
常考题型
例1
利用二倍角公式给角求值的基本思路
(1)直接正用、逆用二倍角公式,结合诱导公式和同角三角函数的基本关系对已知式子进行转化,一般可以化为特殊角.
(2)若形式为几个非特殊角的三角函数式相乘,则一般逆用二倍角的正弦公式,在求解过程中,需利用互余关系配凑出应用二倍角公式的条件,使得问题出现可以连用二倍角的正弦公式的形式.
解题归纳
训练题
<2>条件求值
条件求值问题解法
条件求值问题常有两种解题途径:①对题设条件变形,把条件中的角、函数名向结论中的角、函数名靠拢;②对结论变形,将结论中的角、函数名向题设条件中的角、函数名靠拢,以便将题设条件代入结论.
解题归纳
训练题
D
A
B
二 利用二倍角公式化简
三角函数式的化简要求
①能求出值的应求出值;②使三角函数种数尽量少;③使三角函数式中的项数尽量少;④尽量使分母不含有三角函数;⑤尽量使被开方数不含三角函数.
三角函数式的化简方法
①弦切互化,异名化同名,异角化同角.
②降幂或升幂.
③一个重要结论:(sin θ±cos θ)2=1±sin 2θ.
解题归纳
训练题
A
三 二倍角公式的灵活应用
例4
二倍角公式的应用技巧
二倍角公式在三角函数的求值、化简、证明中应用十分广泛,公式的应用也十分灵活,常见的应用技巧有以下几种:
1.二倍角的相对性:2α是α的二倍;α是的二倍; 是的二倍,如此等等.
2.公式的逆用:二倍角公式的逆用非常广泛,逆用时要特别注意式子的结构特征,有时需要配凑系数或符号.
3.公式的变用:二倍角公式是一组要求很高的公式,不仅要会逆用,还要会变用,特别是二倍角的余弦,变形很多,应熟练掌握.
如sin αcos α=sin 2α;sin 2α-cos 2α=-cos 2α;sin 2α=;cos 2α= 等等.
解题归纳
训练题
BC
四 二倍角公式的综合应用
【 解析】
【答案】A
例5 [2019·河北张家口高一期末]函数f(x)=sin2x+ sin xcos x在区间 上的最大值是 ( )
A. B.1 C. D.
用二倍角公式解决三角函数性质问题的方法
1.为了研究函数的性质,往往要充分利用三角变换公式转化为余弦型(正弦型)函数,这是解决问题的前提.
2.解决有关三角函数的最值问题,一般需利用三角函数的有界性来解决,利用三角函数变换化多个三角函数为一个三角函数.如果含有二次方,一般要换元、配方借助于二次函数解决.
解题归纳
训练题
1. [2019·广东雷州高三期末]当x=θ时,函数f(x)=2+sin x-4cos2 取得最大值,则cos θ= .
解题归纳
小结
1、二倍角正弦、余弦、正切公式的推导
sin 2α=2sin αcos α,
cos 2α=cos2α-sin2α,
.且,
2、注意正 用 、逆用、变形用
cos 2α=1-2sin2α=2cos2α-1.
3、公式变形
升幂降角公式
降幂升角公式
知易行难,重在行动
千里之行,始于足下
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
数学-RJ·A-必修第一册
5.5 三角恒等变换
5.5.1 两角和与差的正弦、余弦和正切公式
第五章 三角函数
学习目标
1.经历用单位圆以及圆的旋转对称性推导出两角差的余弦公式的过程.
2.能从两角差的余弦公式导出两角和与差的正弦、余弦、正切公式,二倍角的正弦、余弦、正切公式,了解它们的内在联系.
3.会用两角和与差的正弦、余弦、正切公式以及二倍角公式进行简单的三角函数的化简、求值、证明.
重点:引导学生通过独立探究和讨论交流,导出两角和与差的三角函数的十一个公式,并了解它们的内在联系,为运用这些公式进行简单的恒等变换打好基础.
难点:两角差的余弦公式的探究.
知识梳理
推导:
sin(α+β)=sin αcos β+cos αsin β,当α=β时,sin 2α=2sin αcos α;
cos(α+β)=cos αcos β-sin αsin β,当α=β时,cos 2α=cos2 α-sin2 α ;
,当α=β时, .
二倍角的正弦、余弦、正切公式
利用S(α±β),C(α±β),T(α±β)推导出sin 2α,cos 2α,tan 2α的公式
课 时 2
通过推导,可以得到:
sin 2α=2sin αcos α, (S2α)
cos 2α=cos2α-sin2α, (C2α)
. (T2α)
如果要求二倍角的余弦公式(C2α)中仅含α的正弦(余弦),那么又可得到:
cos 2α=1-2sin2α, cos 2α=2cos2α-1.
以上这些公式都叫做倍角公式.倍角公式给出了α的三角函数与2α的三角函数之间的关系.(这里的“倍角”专指“二倍角”,遇到“三倍角”等名词时,“三”字等不可省去.)·
二倍角的“广义理解”:二倍角是相对的,如4α是2α的二倍,α是 的二倍等,“倍”是描述两个数量之间的关系的,这里蕴含着换元思想.
对于S2α和C2α,α∈R,但是在使用T2α时,要保证分母1-tan2α≠0且tan α有意义,即α≠kπ+ 且α≠kπ- 且α≠kπ+ (k∈Z).当α=kπ+ 及α=kπ- (k∈Z)时,tan 2α的值不存在;当α=kπ+ (k∈Z)时,tan α的值不存在,故不能用二倍角公式求tan 2α,此时可以利用诱导公式直接求tan 2α.
一般情况下,sin 2α≠2sin α,cos 2α≠2cos α,tan 2α≠2tan α.
倍角公式的逆用更能开拓思路,我们要熟悉这组公式的逆用,如sin 3αcos 3α= sin 6α.
从和(差)角公式、倍角公式的推导过程可以发现,归纳总结这些公式存在紧密的逻辑联系:
一 利用二倍角公式求值
<1>给角求值
常考题型
例1
利用二倍角公式给角求值的基本思路
(1)直接正用、逆用二倍角公式,结合诱导公式和同角三角函数的基本关系对已知式子进行转化,一般可以化为特殊角.
(2)若形式为几个非特殊角的三角函数式相乘,则一般逆用二倍角的正弦公式,在求解过程中,需利用互余关系配凑出应用二倍角公式的条件,使得问题出现可以连用二倍角的正弦公式的形式.
解题归纳
训练题
<2>条件求值
条件求值问题解法
条件求值问题常有两种解题途径:①对题设条件变形,把条件中的角、函数名向结论中的角、函数名靠拢;②对结论变形,将结论中的角、函数名向题设条件中的角、函数名靠拢,以便将题设条件代入结论.
解题归纳
训练题
D
A
B
二 利用二倍角公式化简
三角函数式的化简要求
①能求出值的应求出值;②使三角函数种数尽量少;③使三角函数式中的项数尽量少;④尽量使分母不含有三角函数;⑤尽量使被开方数不含三角函数.
三角函数式的化简方法
①弦切互化,异名化同名,异角化同角.
②降幂或升幂.
③一个重要结论:(sin θ±cos θ)2=1±sin 2θ.
解题归纳
训练题
A
三 二倍角公式的灵活应用
例4
二倍角公式的应用技巧
二倍角公式在三角函数的求值、化简、证明中应用十分广泛,公式的应用也十分灵活,常见的应用技巧有以下几种:
1.二倍角的相对性:2α是α的二倍;α是的二倍; 是的二倍,如此等等.
2.公式的逆用:二倍角公式的逆用非常广泛,逆用时要特别注意式子的结构特征,有时需要配凑系数或符号.
3.公式的变用:二倍角公式是一组要求很高的公式,不仅要会逆用,还要会变用,特别是二倍角的余弦,变形很多,应熟练掌握.
如sin αcos α=sin 2α;sin 2α-cos 2α=-cos 2α;sin 2α=;cos 2α= 等等.
解题归纳
训练题
BC
四 二倍角公式的综合应用
【 解析】
【答案】A
例5 [2019·河北张家口高一期末]函数f(x)=sin2x+ sin xcos x在区间 上的最大值是 ( )
A. B.1 C. D.
用二倍角公式解决三角函数性质问题的方法
1.为了研究函数的性质,往往要充分利用三角变换公式转化为余弦型(正弦型)函数,这是解决问题的前提.
2.解决有关三角函数的最值问题,一般需利用三角函数的有界性来解决,利用三角函数变换化多个三角函数为一个三角函数.如果含有二次方,一般要换元、配方借助于二次函数解决.
解题归纳
训练题
1. [2019·广东雷州高三期末]当x=θ时,函数f(x)=2+sin x-4cos2 取得最大值,则cos θ= .
解题归纳
小结
1、二倍角正弦、余弦、正切公式的推导
sin 2α=2sin αcos α,
cos 2α=cos2α-sin2α,
.且,
2、注意正 用 、逆用、变形用
cos 2α=1-2sin2α=2cos2α-1.
3、公式变形
升幂降角公式
降幂升角公式
知易行难,重在行动
千里之行,始于足下
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
