【课件】4.2 指数函数 高中数学-RJA-必修第一册 (共43张PPT)
文档属性
| 名称 | 【课件】4.2 指数函数 高中数学-RJA-必修第一册 (共43张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-18 00:00:00 | ||
图片预览










文档简介
(共42张PPT)
数学-RJ·A-必修第一册
4.2 指数函数
第四章 指数函数与对数函数
学习目标
1.理解指数函数的概念与意义.
2.能借助计算器与计算机画出具体指数函数的图象,探索并理解指数函数的单调性与特殊点.
3.在解决实际问题的过程中,体会指数函数是一类重要的函数模型.
重点:指数函数的概念和图象.
难点:指数函数性质的应用.
知识梳理
一般地,函数(>0,且≠1)叫做指数函数,其中指数是自变量,定义域是R.
一、指数函数的概念
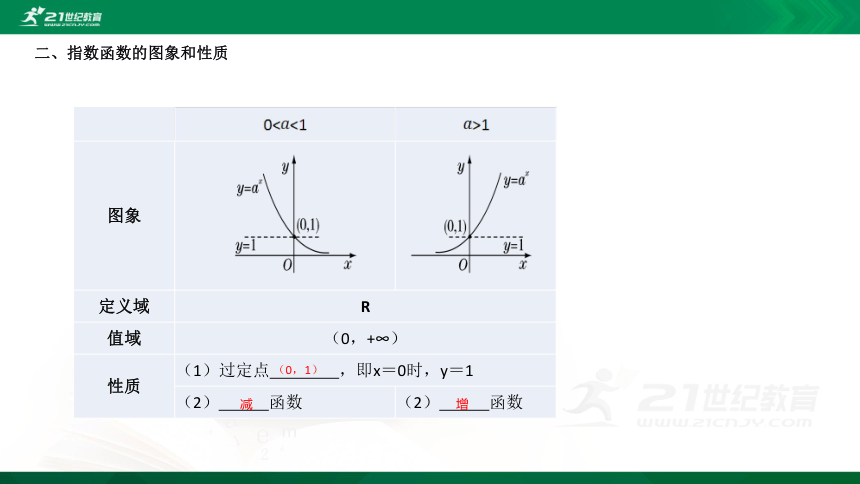
二、指数函数的图象和性质
0<<1 >1
图象
定义域 R 值域 (0,+∞) 性质 (1)过定点 ,即x=0时,y=1 (2) 函数 (2) 函数
增
减
(0,1)
一 指数函数的概念
常考题型
例1 函数·是指数函数,则的值为( )
A.1或2 B.1
C.2 D.>0且≠1的所有实数
【解析】 ∵·是指数函数,∴=1, 解得a=2,故选C.
【答案】 C
◆指数函数的判断方法
1.看形式,判断一个函数是否为指数函数,关键是看解析式是否符合y=ax(a>0,且a≠1)这一结构形式.
2.明特征,指数函数y=ax具有以下特征:
①底数a为大于0且不等于1的实数;
②指数位置是自变量x,且x的系数是1;
③ax的系数是1.
◆正确区分指数函数和指数型函数
1.形如y=ax(a>0且a≠1)的是指数函数.
2.形如y=b·ax+c(a>0,a≠1,b≠0,c≠0)的是指数型函数.
训练题
1.下列函数中为指数函数的有( )
①;②y= ;③;④(>0且≠1);⑤;⑥;⑦.
A.2个 B.3个 C.4个 D.5个
A
A
二、指数函数的图象及其应用
1.图象的画法及识别
例2 [2020·辽宁大连育明高中高一检测]若函数f(x)=(x-a)(x-b)(a>b)的图象如图所示,则g(x)=a-x+b的图象可能是 ( )
A B C D
【解析】根据函数f(x)=(x-a)(x-b)(a>b)的图象知
a>1,-1根据函数平移变换知选项C满足条件,故选C.
【答案】C
◆指数(型)函数图象的画法
1.三点法
在平面直角坐标系上通过描出,(0,1)(1,a)三个点并连线,从而画出指数函数的大致图象.
2.变换作图法
(1)平移变换:将函数y=f(x)的图象向右平移m(m>0)个单位长度得到函数y=f(x-m)的图象(若m<0,就是向左平移|m|个单位长度),将函数y=f (x)的图象向上平移n(n>0)个单位长度,得到函数y=f(x)+n的图象(若n<0,则向下平移|n|个单位长度).
(2)对称变换:
①函数y=f(x)的图象与函数y=f(-x)的图象关于y轴对称,函数y=f(x)的图象与函数y=-f(x)的图象关于x轴对称,函数y=f(x)的图象与函数y=-f(-x)的图象关于原点对称.
②函数y=f(|x|)是一个偶函数,其图象关于y轴对称,是将函数y=f(x)位于y轴右侧的图象保留,然后将y轴右侧的图象沿y轴翻折到左侧,就得到函数y=f(|x|)的图象.
③函数y=|f(x)|的图象是将函数y=f(x)的图象在x轴下方的部分沿x轴翻折到上方,x轴上方的部分不变.
训练题
1.[2020·天津一中高二期末]已知函数f(x)=3-x+a的图象经过第二、三、四象限,g(a)=f(a)-f(a+1),则g(a)的取值范围是 .
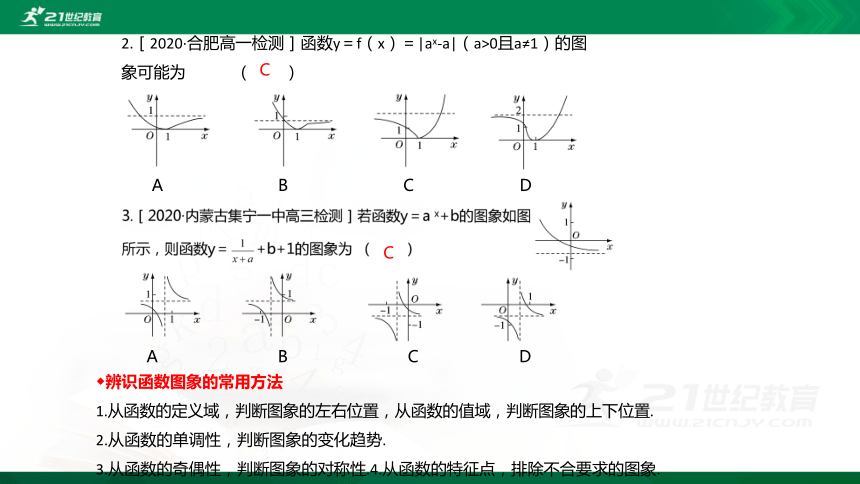
2.[2020·合肥高一检测]函数y=f(x)=|ax-a|(a>0且a≠1)的图象可能为 ( )
A B C D
A B C D
C
C
◆辨识函数图象的常用方法
1.从函数的定义域,判断图象的左右位置,从函数的值域,判断图象的上下位置.
2.从函数的单调性,判断图象的变化趋势.
3.从函数的奇偶性,判断图象的对称性.4.从函数的特征点,排除不合要求的图象.
2. 图象过定点问题
例3 [2019·山东师范大学附属中学高一检测]函数的图象恒过点 .
【解析】当,即时,为常数,此时=1-4=-3,即函数 的图象恒过点.
【答案】
◆指数型函数图象过定点问题的思路
由于指数函数y=ax(a>0,且a≠1)的图象过定点(0,1),因此讨论与指数函数有关的函数图象过定点问题,我们只需令指数为0,解出相应的x,y的值,即可确定定点的坐标.
训练题 [2019·沈阳高一期末]函数f(x)=2ax+2-1(a>0,且a≠1)的图象恒过的点坐标是 ( )
A.(-2,-1) B.(-2,1) C.(-1,-1) D.(-1,1)
B
3. 图象的应用
例4 [2020·云南省玉溪第一中学高一检测]已知f(x)=|3x-1|+1,若关于x的方程[f(x)]2-(2+a)f(x)+2a=0有三个实根,则实数a的取值范围是 ( )
A.12 C.21
【解题提示】由题得f(x)=2或f(x)=a,|3x-1|=1有一个解,命题等价于方程|3x-1|=a-1有两个不同的实根,利用数形结合求出a的取值范围.
【解析】由题得[f(x)-2][f(x)-a]=0,
所以f(x)=2或f(x)=a,所以|3x-1|+1=2或|3x-1|+1=a,
所以|3x-1|=1或|3x-1|=a-1,|3x-1|=1 有一个根,
所以方程|3x-1|=a-1有两个不同的实根,
函数y=|3x-1|的图象如图所示,所以0故选A.
【答案】A
◆应用函数图象的常用方法
1.抓住图象上的特殊点;
2.利用图象的变换;
3.利用函数的奇偶性与单调性.
训练题
1.若直线与函数(>0,且≠1)的图象有两个公共点,则的取值
范围是 .
A
三、与指数函数有关的定义域和值域问题
1.形如的函数的定义域和值域
【解】(1)由-4≠0,得≠4,∴的定义域为{|∈R,且≠4}.
又≠0,即 ≠1,∴ 的值域为{|>0,且≠1}.
(2)函数的定义域为R.∵ x2-2x-3=(x-1)2-4≥-4,
∴ ≤=16.又∵ >0,∴ y= 的值域为(0,16].
例5 求下列函数的定义域和值域.
(1); (2).
◆形如的函数的定义域和值域的求法
1.函数y=a f(x)的定义域与函数f(x)的定义域相同;
2.求函数y=a f(x)的值域,需先确定函数f(x)的值域,再根据指数函数y=ax的单调性确定函数y=a f(x)的值域.
2.[2019·江西新余四中高一检测]求下列函数的定义域和值域.
(1); (2) .
[解](1)定义域为R.
∵ ≥0,∴ = ≥ =1.
∴ 值域为{|≥1}.
(2)定义域为R.∵ ,∴ ≤2,即≤2.
故函数的值域为(0,2].
{x|x≠±1}
∪(1,+∞)
2.形如的函数的定义域和值域
【答案】(1)A (2)D
◆形如y=f(ax)的函数的定义域和值域的求法
1.求函数y=f(ax)的定义域,需先确定函数y=f(u)的定义域,即u的取值范围,亦即函数u=ax的值域,由此构造关于x的不等式(组)确定x的取值范围,得到函数y=f(ax)的定义域;
2.求函数y=f(ax)的值域,需先利用函数u=ax的单调性确定u的取值范围,再确定函数y=f(u)的值域,即为函数y=f(ax)的值域.
【知识拓展】
设x为任意一个实数,y是不超过x的最大整数,则这种对应关系是一个函数,通常称为取整函数,也叫高斯函数,记作y=[x].
其定义域是R,值域为Z,图象为“阶梯曲线”.
训练题
A
2.已知求函数的最值.
【解】 .
∵ ,∴ ,∴.
∴ 当,即=1时,取得最小值;
当=4,即时,取得最大值13.
四 指数函数的性质及其应用
1. 利用指数函数的单调性研究最值问题
例7 已知函数在[1,2]上的最大值比最小值大,求的值.
【解】①当00,a≠1)在[1,2]上的最大值f(x)max=f(1)=a1=a,最小值f(x)min=f(2)=a2,∴ a-a2=,解得a=或a=0(舍去).
②当a>1时,函数f(x)=ax(a>0,a≠1)在[1,2]上的最大值f(x)max=f(2)=a2,最小值f(x)min=f(1)=a1=a,∴ a2-a=,解得a=或a=0(舍去).
综上所述,a的值为或.
◆指数函数的最值问题
由于指数函数在定义域R上是单调函数,因此在R上的子集——闭区间上也是单调函数,且在闭区间的两个端点处分别取到最大值和最小值,应特别注意的是,当底数未知时,要对底数分情况讨论.
训练题
A
2. 利用指数函数的单调性比较大小
例8 [2019·浙江台州书生中学高一月考]已知a=0.3-2,b=,c=,则a,b,c的大小关系是 ( )
A.a>b>c B.a>c>b C.c>b>a D.b>a>c
【解析】 ∵ b=1,∴ a>c>b.故选B.
【答案】 B
◆利用指数函数的单调性比较大小的方法
1.比较两个幂的大小常用的方法:
①作差(商)法;②函数单调性法;③中间值法.
2.注意点:①对于底数相同,指数不同的两个幂,可以利用指数函数的单调性来比较.②对于底数不同,指数相同的两个幂,可以利用指数函数图象的变化规律来比较.③对于底数不同且指数也不同的两个幂,可以通过中间值来比较.
④对于三个(或三个以上的)数,则应先根据值的大小(特别是与0,1作大小比较)进行分组,再比较各组数的大小.
训练题
1.已知a=22.5,b=2.50,c=,则a,b,c的大小关系是( )
A.a>c>b B.c>a>b C.b>a>c D.a>b>c
2.[2019·山东师范大学附属中学高一检测]设y1=40.9,y2=80.61,y3=,则( )
A.y1>y2>y3 B.y2>y1>y3 C.y1>y3>y2 D.y3>y2>y1
3. 利用指数函数的单调性解不等式问题
例9 [2019·内蒙古鄂尔多斯高三检测]不等式>3-2x的解集是( )
A.{x|-2-2}
【解题提示】 利用指数函数的单调性化指数不等式为一元二次不等式求解.
【解析】 由 >3-2x,得 >3-2x,∴ 8-x2>-2x,即x2-2x-8<0,
解得-2∴ 不等式 >3-2x的解集是{x|-2【答案】 A
◆指数不等式的类型及解法
1.形如ax>ay的不等式,借助函数y=ax的单调性求解,如果a的取值不确定,那么需分a>1和02.形如ax>b的不等式,应先将b化成以a为底的指数幂的形式,再借助函数y=ax的单调性求解.
3.形如ax>bx的不等式,需利用函数图象求解.
A
五 指数型复合函数的单调性和奇偶性
1. 指数型复合函数的单调性和最值问题
例10 [2019·吉林省实验中学高一检测]函数f(x)= 的单调减区间为( )
A.(-∞,2] B.[1,2]
C.[2,+∞) D.[2,3]
【解析】 由题中的复合函数的底数大于0且小于1,
知要求g(x)=的增区间.
画出二次函数h(x)=-x2+4x-3的图象如图所示.
由二次函数单调性及二次根式有意义的条件可知1≤x≤2.所以选B.
【答案】 B
◆求解指数型复合函数的单调性的一般方法
1.指数函数y=ax(a>0且a≠1)的单调性与底数有关,因此讨论指数函数的单调性时,一定要明确底数与1的大小关系,当01时,y=ax为单调增函数.
2.与指数函数有关的函数的单调性也往往与底数有关,解决方法一般是利用函数单调性的定义.
3.特别地,对于形如f(x)=a g(x)(a>0且a≠1)的函数,可以利用复合函数的单调性,先判断指数函数y=a x及函数g(x)在定义域内的单调性,再根据“同增异减”得出f(x)的单调性.
训练题
1. 判断函数y=的单调性.
2.[2019·河北辛集高一检测]函数f(x)=在区间[1,2]上是减函数,则实数a的取值范围是( )
A.a≤-4 B.a≤-2 C.a≥-2 D.a>-4
【解】令t=,t>0,则y=t2-2t+2.
又t= 在R上是减函数,y=t2-2t+2在(0,1]上是减函数,在[1,+∞)上是增函数,
所以函数y= 在(-∞,0]上是减函数,在[0,+∞)上是增函数.
2. 指数型复合函数的奇偶性和单调性的综合问题
例11 [2019·安徽江淮名校高三联考]已知函数f(x)=,则f(x)是( )
A.奇函数,且在R上是增函数 B.偶函数,且在(0,+∞)上是增函数
C.奇函数,且在R上是减函数 D.偶函数,且在(0,+∞)上是减函数
【解题提示】 先判断定义域是否关于原点对称,进而利用f(-x)±f(x)与0的关系可得函数的奇偶性,再由复合函数单调性的判断方法可判断函数的单调性.
【解析】 f(x)的定义域为R,关于原点对称,
f(-x)= =有f(-x)+f(x)=0,
所以f(x)是奇函数,函数f(x)=显然是减函数.
【答案】 C
◆判断函数奇偶性要注意的问题
1.坚持“定义域优先”的原则.
如果定义域不关于原点对称,那么可立刻判定此函数既不是奇函数也不是偶函数.
2.正确利用变形技巧.
分析f(x)和f(-x)的关系,必要时可利用f(x)±f(-x)=0判定.
3.巧用图象的特征.
在解答有图象信息的选择题时,可根据奇函数的图象关于原点对称,偶函数的图象关于y轴对称,进行快速判定.
训练题
2.已知函数f(x)=(a>1).
(1)判断函数f(x)的奇偶性.
(2)证明f(x)在(-∞,+∞)上是增函数.
(3)求f(x)的值域.
(1)【解】函数的定义域为.
f(-x)= = ==-f(x),所以函数f(x)是奇函数.
()
(2) 【证明】 f(x)= = =1- ,
任取x1,x2∈R,且x1因为a>1,x10,,
所以f(x1)-f(x2)<0,即f(x1)(3) 【解】 (方法一:直接法)由(2)得f(x)=1- .因为ax>0,所以ax+1>1,所以0< <1,所以0< <2,所以-1<1- <1,所以f (x)的值域为(-1,1).
(方法二:反表示法)令y= ,得yax+y=ax-1,即(1-y)ax=y+1,所以ax=>0,
所以-1小结
1.指数函数的概念
指数函数的结构特征
(1)解析式中ax的系数为1;(2)底数a是常数,满足a>0,且a≠1;
(3)自变量x是指数,且x∈R.
2.指数函数的图象与性质
0<<1 >1
图象
定义域 R 值域 (0,+∞) 性质 (1)过定点(0,1),即x=0时,y=1 (2)减函数 (2)增函数
(1)常用结论
(1)y=f(x)与y=f(-x)的图象关于y轴对称.
(2)y=f(x)与y=-f(x)的图象关于x轴对称.
(3)y=f(x)与y=-f(-x)的图象关于原点对称.
(2)指数函数性质的记忆口诀
指数增减要看清,抓住底数不放松;
底数总是大于0,不等于1已表明;
底数若是大于1,图象从下往上增;
底数0到1之间,图象从上往下减;
无论函数增和减,图象都过(0,1)点.
3.指数函数性质的应用
比较幂值大小的方法
(1)底数相同、指数不同:利用指数函数的单调性解决.
(2)底数不同、指数相同:利用指数函数的图象解决.在同一平面直角坐标系中画出各个函数的图象,依据底数a对指数函数图象的影响,按照逆时针方向观察,底数在逐渐增大,然后观察指数取值所对应的函数值即可.
(3)底数不同、指数也不同:采用介值法(中间值法).取中间值1,其中一个大于1,另一个小于1.
谢谢
数学-RJ·A-必修第一册
4.2 指数函数
第四章 指数函数与对数函数
学习目标
1.理解指数函数的概念与意义.
2.能借助计算器与计算机画出具体指数函数的图象,探索并理解指数函数的单调性与特殊点.
3.在解决实际问题的过程中,体会指数函数是一类重要的函数模型.
重点:指数函数的概念和图象.
难点:指数函数性质的应用.
知识梳理
一般地,函数(>0,且≠1)叫做指数函数,其中指数是自变量,定义域是R.
一、指数函数的概念
二、指数函数的图象和性质
0<<1 >1
图象
定义域 R 值域 (0,+∞) 性质 (1)过定点 ,即x=0时,y=1 (2) 函数 (2) 函数
增
减
(0,1)
一 指数函数的概念
常考题型
例1 函数·是指数函数,则的值为( )
A.1或2 B.1
C.2 D.>0且≠1的所有实数
【解析】 ∵·是指数函数,∴=1, 解得a=2,故选C.
【答案】 C
◆指数函数的判断方法
1.看形式,判断一个函数是否为指数函数,关键是看解析式是否符合y=ax(a>0,且a≠1)这一结构形式.
2.明特征,指数函数y=ax具有以下特征:
①底数a为大于0且不等于1的实数;
②指数位置是自变量x,且x的系数是1;
③ax的系数是1.
◆正确区分指数函数和指数型函数
1.形如y=ax(a>0且a≠1)的是指数函数.
2.形如y=b·ax+c(a>0,a≠1,b≠0,c≠0)的是指数型函数.
训练题
1.下列函数中为指数函数的有( )
①;②y= ;③;④(>0且≠1);⑤;⑥;⑦.
A.2个 B.3个 C.4个 D.5个
A
A
二、指数函数的图象及其应用
1.图象的画法及识别
例2 [2020·辽宁大连育明高中高一检测]若函数f(x)=(x-a)(x-b)(a>b)的图象如图所示,则g(x)=a-x+b的图象可能是 ( )
A B C D
【解析】根据函数f(x)=(x-a)(x-b)(a>b)的图象知
a>1,-1
【答案】C
◆指数(型)函数图象的画法
1.三点法
在平面直角坐标系上通过描出,(0,1)(1,a)三个点并连线,从而画出指数函数的大致图象.
2.变换作图法
(1)平移变换:将函数y=f(x)的图象向右平移m(m>0)个单位长度得到函数y=f(x-m)的图象(若m<0,就是向左平移|m|个单位长度),将函数y=f (x)的图象向上平移n(n>0)个单位长度,得到函数y=f(x)+n的图象(若n<0,则向下平移|n|个单位长度).
(2)对称变换:
①函数y=f(x)的图象与函数y=f(-x)的图象关于y轴对称,函数y=f(x)的图象与函数y=-f(x)的图象关于x轴对称,函数y=f(x)的图象与函数y=-f(-x)的图象关于原点对称.
②函数y=f(|x|)是一个偶函数,其图象关于y轴对称,是将函数y=f(x)位于y轴右侧的图象保留,然后将y轴右侧的图象沿y轴翻折到左侧,就得到函数y=f(|x|)的图象.
③函数y=|f(x)|的图象是将函数y=f(x)的图象在x轴下方的部分沿x轴翻折到上方,x轴上方的部分不变.
训练题
1.[2020·天津一中高二期末]已知函数f(x)=3-x+a的图象经过第二、三、四象限,g(a)=f(a)-f(a+1),则g(a)的取值范围是 .
2.[2020·合肥高一检测]函数y=f(x)=|ax-a|(a>0且a≠1)的图象可能为 ( )
A B C D
A B C D
C
C
◆辨识函数图象的常用方法
1.从函数的定义域,判断图象的左右位置,从函数的值域,判断图象的上下位置.
2.从函数的单调性,判断图象的变化趋势.
3.从函数的奇偶性,判断图象的对称性.4.从函数的特征点,排除不合要求的图象.
2. 图象过定点问题
例3 [2019·山东师范大学附属中学高一检测]函数的图象恒过点 .
【解析】当,即时,为常数,此时=1-4=-3,即函数 的图象恒过点.
【答案】
◆指数型函数图象过定点问题的思路
由于指数函数y=ax(a>0,且a≠1)的图象过定点(0,1),因此讨论与指数函数有关的函数图象过定点问题,我们只需令指数为0,解出相应的x,y的值,即可确定定点的坐标.
训练题 [2019·沈阳高一期末]函数f(x)=2ax+2-1(a>0,且a≠1)的图象恒过的点坐标是 ( )
A.(-2,-1) B.(-2,1) C.(-1,-1) D.(-1,1)
B
3. 图象的应用
例4 [2020·云南省玉溪第一中学高一检测]已知f(x)=|3x-1|+1,若关于x的方程[f(x)]2-(2+a)f(x)+2a=0有三个实根,则实数a的取值范围是 ( )
A.1
【解题提示】由题得f(x)=2或f(x)=a,|3x-1|=1有一个解,命题等价于方程|3x-1|=a-1有两个不同的实根,利用数形结合求出a的取值范围.
【解析】由题得[f(x)-2][f(x)-a]=0,
所以f(x)=2或f(x)=a,所以|3x-1|+1=2或|3x-1|+1=a,
所以|3x-1|=1或|3x-1|=a-1,|3x-1|=1 有一个根,
所以方程|3x-1|=a-1有两个不同的实根,
函数y=|3x-1|的图象如图所示,所以0
【答案】A
◆应用函数图象的常用方法
1.抓住图象上的特殊点;
2.利用图象的变换;
3.利用函数的奇偶性与单调性.
训练题
1.若直线与函数(>0,且≠1)的图象有两个公共点,则的取值
范围是 .
A
三、与指数函数有关的定义域和值域问题
1.形如的函数的定义域和值域
【解】(1)由-4≠0,得≠4,∴的定义域为{|∈R,且≠4}.
又≠0,即 ≠1,∴ 的值域为{|>0,且≠1}.
(2)函数的定义域为R.∵ x2-2x-3=(x-1)2-4≥-4,
∴ ≤=16.又∵ >0,∴ y= 的值域为(0,16].
例5 求下列函数的定义域和值域.
(1); (2).
◆形如的函数的定义域和值域的求法
1.函数y=a f(x)的定义域与函数f(x)的定义域相同;
2.求函数y=a f(x)的值域,需先确定函数f(x)的值域,再根据指数函数y=ax的单调性确定函数y=a f(x)的值域.
2.[2019·江西新余四中高一检测]求下列函数的定义域和值域.
(1); (2) .
[解](1)定义域为R.
∵ ≥0,∴ = ≥ =1.
∴ 值域为{|≥1}.
(2)定义域为R.∵ ,∴ ≤2,即≤2.
故函数的值域为(0,2].
{x|x≠±1}
∪(1,+∞)
2.形如的函数的定义域和值域
【答案】(1)A (2)D
◆形如y=f(ax)的函数的定义域和值域的求法
1.求函数y=f(ax)的定义域,需先确定函数y=f(u)的定义域,即u的取值范围,亦即函数u=ax的值域,由此构造关于x的不等式(组)确定x的取值范围,得到函数y=f(ax)的定义域;
2.求函数y=f(ax)的值域,需先利用函数u=ax的单调性确定u的取值范围,再确定函数y=f(u)的值域,即为函数y=f(ax)的值域.
【知识拓展】
设x为任意一个实数,y是不超过x的最大整数,则这种对应关系是一个函数,通常称为取整函数,也叫高斯函数,记作y=[x].
其定义域是R,值域为Z,图象为“阶梯曲线”.
训练题
A
2.已知求函数的最值.
【解】 .
∵ ,∴ ,∴.
∴ 当,即=1时,取得最小值;
当=4,即时,取得最大值13.
四 指数函数的性质及其应用
1. 利用指数函数的单调性研究最值问题
例7 已知函数在[1,2]上的最大值比最小值大,求的值.
【解】①当0
②当a>1时,函数f(x)=ax(a>0,a≠1)在[1,2]上的最大值f(x)max=f(2)=a2,最小值f(x)min=f(1)=a1=a,∴ a2-a=,解得a=或a=0(舍去).
综上所述,a的值为或.
◆指数函数的最值问题
由于指数函数在定义域R上是单调函数,因此在R上的子集——闭区间上也是单调函数,且在闭区间的两个端点处分别取到最大值和最小值,应特别注意的是,当底数未知时,要对底数分情况讨论.
训练题
A
2. 利用指数函数的单调性比较大小
例8 [2019·浙江台州书生中学高一月考]已知a=0.3-2,b=,c=,则a,b,c的大小关系是 ( )
A.a>b>c B.a>c>b C.c>b>a D.b>a>c
【解析】 ∵ b=
【答案】 B
◆利用指数函数的单调性比较大小的方法
1.比较两个幂的大小常用的方法:
①作差(商)法;②函数单调性法;③中间值法.
2.注意点:①对于底数相同,指数不同的两个幂,可以利用指数函数的单调性来比较.②对于底数不同,指数相同的两个幂,可以利用指数函数图象的变化规律来比较.③对于底数不同且指数也不同的两个幂,可以通过中间值来比较.
④对于三个(或三个以上的)数,则应先根据值的大小(特别是与0,1作大小比较)进行分组,再比较各组数的大小.
训练题
1.已知a=22.5,b=2.50,c=,则a,b,c的大小关系是( )
A.a>c>b B.c>a>b C.b>a>c D.a>b>c
2.[2019·山东师范大学附属中学高一检测]设y1=40.9,y2=80.61,y3=,则( )
A.y1>y2>y3 B.y2>y1>y3 C.y1>y3>y2 D.y3>y2>y1
3. 利用指数函数的单调性解不等式问题
例9 [2019·内蒙古鄂尔多斯高三检测]不等式>3-2x的解集是( )
A.{x|-2
【解题提示】 利用指数函数的单调性化指数不等式为一元二次不等式求解.
【解析】 由 >3-2x,得 >3-2x,∴ 8-x2>-2x,即x2-2x-8<0,
解得-2
◆指数不等式的类型及解法
1.形如ax>ay的不等式,借助函数y=ax的单调性求解,如果a的取值不确定,那么需分a>1和0
3.形如ax>bx的不等式,需利用函数图象求解.
A
五 指数型复合函数的单调性和奇偶性
1. 指数型复合函数的单调性和最值问题
例10 [2019·吉林省实验中学高一检测]函数f(x)= 的单调减区间为( )
A.(-∞,2] B.[1,2]
C.[2,+∞) D.[2,3]
【解析】 由题中的复合函数的底数大于0且小于1,
知要求g(x)=的增区间.
画出二次函数h(x)=-x2+4x-3的图象如图所示.
由二次函数单调性及二次根式有意义的条件可知1≤x≤2.所以选B.
【答案】 B
◆求解指数型复合函数的单调性的一般方法
1.指数函数y=ax(a>0且a≠1)的单调性与底数有关,因此讨论指数函数的单调性时,一定要明确底数与1的大小关系,当0
2.与指数函数有关的函数的单调性也往往与底数有关,解决方法一般是利用函数单调性的定义.
3.特别地,对于形如f(x)=a g(x)(a>0且a≠1)的函数,可以利用复合函数的单调性,先判断指数函数y=a x及函数g(x)在定义域内的单调性,再根据“同增异减”得出f(x)的单调性.
训练题
1. 判断函数y=的单调性.
2.[2019·河北辛集高一检测]函数f(x)=在区间[1,2]上是减函数,则实数a的取值范围是( )
A.a≤-4 B.a≤-2 C.a≥-2 D.a>-4
【解】令t=,t>0,则y=t2-2t+2.
又t= 在R上是减函数,y=t2-2t+2在(0,1]上是减函数,在[1,+∞)上是增函数,
所以函数y= 在(-∞,0]上是减函数,在[0,+∞)上是增函数.
2. 指数型复合函数的奇偶性和单调性的综合问题
例11 [2019·安徽江淮名校高三联考]已知函数f(x)=,则f(x)是( )
A.奇函数,且在R上是增函数 B.偶函数,且在(0,+∞)上是增函数
C.奇函数,且在R上是减函数 D.偶函数,且在(0,+∞)上是减函数
【解题提示】 先判断定义域是否关于原点对称,进而利用f(-x)±f(x)与0的关系可得函数的奇偶性,再由复合函数单调性的判断方法可判断函数的单调性.
【解析】 f(x)的定义域为R,关于原点对称,
f(-x)= =有f(-x)+f(x)=0,
所以f(x)是奇函数,函数f(x)=显然是减函数.
【答案】 C
◆判断函数奇偶性要注意的问题
1.坚持“定义域优先”的原则.
如果定义域不关于原点对称,那么可立刻判定此函数既不是奇函数也不是偶函数.
2.正确利用变形技巧.
分析f(x)和f(-x)的关系,必要时可利用f(x)±f(-x)=0判定.
3.巧用图象的特征.
在解答有图象信息的选择题时,可根据奇函数的图象关于原点对称,偶函数的图象关于y轴对称,进行快速判定.
训练题
2.已知函数f(x)=(a>1).
(1)判断函数f(x)的奇偶性.
(2)证明f(x)在(-∞,+∞)上是增函数.
(3)求f(x)的值域.
(1)【解】函数的定义域为.
f(-x)= = ==-f(x),所以函数f(x)是奇函数.
()
(2) 【证明】 f(x)= = =1- ,
任取x1,x2∈R,且x1
所以f(x1)-f(x2)<0,即f(x1)
(方法二:反表示法)令y= ,得yax+y=ax-1,即(1-y)ax=y+1,所以ax=>0,
所以-1
1.指数函数的概念
指数函数的结构特征
(1)解析式中ax的系数为1;(2)底数a是常数,满足a>0,且a≠1;
(3)自变量x是指数,且x∈R.
2.指数函数的图象与性质
0<<1 >1
图象
定义域 R 值域 (0,+∞) 性质 (1)过定点(0,1),即x=0时,y=1 (2)减函数 (2)增函数
(1)常用结论
(1)y=f(x)与y=f(-x)的图象关于y轴对称.
(2)y=f(x)与y=-f(x)的图象关于x轴对称.
(3)y=f(x)与y=-f(-x)的图象关于原点对称.
(2)指数函数性质的记忆口诀
指数增减要看清,抓住底数不放松;
底数总是大于0,不等于1已表明;
底数若是大于1,图象从下往上增;
底数0到1之间,图象从上往下减;
无论函数增和减,图象都过(0,1)点.
3.指数函数性质的应用
比较幂值大小的方法
(1)底数相同、指数不同:利用指数函数的单调性解决.
(2)底数不同、指数相同:利用指数函数的图象解决.在同一平面直角坐标系中画出各个函数的图象,依据底数a对指数函数图象的影响,按照逆时针方向观察,底数在逐渐增大,然后观察指数取值所对应的函数值即可.
(3)底数不同、指数也不同:采用介值法(中间值法).取中间值1,其中一个大于1,另一个小于1.
谢谢
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
