【课件】2.3二次函数与一元二次方程、不等式 高中数学-RJA-必修第一册 (共36张PPT)
文档属性
| 名称 | 【课件】2.3二次函数与一元二次方程、不等式 高中数学-RJA-必修第一册 (共36张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-19 17:30:14 | ||
图片预览











文档简介
(共36张PPT)
数学-RJ·A-必修第一册
2.3二次函数与一元二次方程、不等式
第二章 一元二次函数、方程和不等式
学习目标
1.经历从实际情境中抽象出一元二次不等式模型的过程.
2.通过函数图象了解一元二次不等式与相应函数、方程的联系.
3.会解一元二次不等式.
重点:从实际问题中抽象出一元二次不等式模型,围绕一元二次不等式的解法展开,突出体现数形结合思想.
难点:理解二次函数、一元二次方程与一元二次不等式的联系.
知识梳理
一个
2
一、一元二次不等式
1.一元二次不等式的概念
解集
二、二次函数的零点
一般地,对于二次函数y=ax2+bx+c,我们把使ax2+bx+c=0的实数x叫作二次函数y=ax2+bx+c的零点.
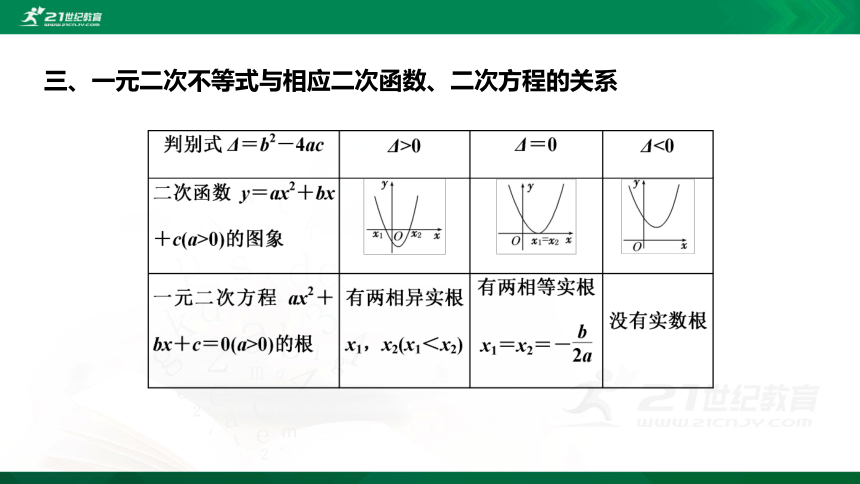
三、一元二次不等式与相应二次函数、二次方程的关系
例1 解不等式:(1)-3x2+6x-2>0;(2)4x2-4x+1≤0.
题组一 不含参数的一元二次不等式的解法
常考题型
(1)
(2)
解题归纳
解不含参数的一元二次不等式的步骤
1.通过对不等式的变形,使不等式右侧为0,使二次项系数为正.
2.对不等式左侧因式分解,若不易分解,则计算对应方程的判别式.
3.求出相应的一元二次方程的根或根据判别式说明方程有无实根.
4.根据一元二次方程根的情况画出对应的二次函数图象的草图.
5.根据图象写出不等式的解集.
记忆口诀:
设相应的二次函数的图象开口向上,并与x轴相交,则有口诀:大于取两边;小于取中间.
1. [2020·江苏南师附中高一检测]已知集合 U=R ,集合A={x|x2-3x+2>0},则UA=( )
A.(1,2) B.[1,2] C.(-2,-1) D.[ -2,-1]
2. “x2-3x+2<0”是“x<2”成立的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
B
A
巩固训练
题型二 简单分式不等式的解法
例2
解题归纳
1.若集合A=,B={x|-1A.[-2,2) B.(-1,1]
C.(-1,1) D.(-1,2)
2.不等式 ≤x-2的解集是 ( )
A.(-∞,0]∪(2,4] B.[0,2)∪[4,+∞)
C.[2,4) D.(-∞,2]∪(4,+∞)
B
C
巩固训练
例3 [2020·上海华东师范大学第一附属中学高二检测]解关于x的不等式ax2-2≥2x-ax(a∈R).
题组三 含参数的一元二次不等式的解法
【解题提示】 将原不等式化为(ax-2)(x+1)≥0,对参数a分5种情况讨论:a=0,a>0,-21.
巩固训练
B
2.
解题归纳
解含参数的一元二次不等式的步骤
1.若二次项含有参数,应先讨论参数是等于0、小于0,还是大于0,然后整理不等式;
2.当二次项系数不为0时,讨论判别式与0的关系,判断方程的根的个数;
3.确定无根时可直接写出解集,确定方程有两个根时,要讨论两根的大小关系,从而确定解集的形式.
例4 若不等式(m+1)x2-(m-1)x+3(m-1)<0对任何实数x恒成立,求实数m的取值范围.
题组四 一元二次不等式的恒成立问题
巩固训练
(1) 对于任意实数x,不等式(a-2)x2- 2(a-2)x-4<0恒成立,则实数a的取值范围是( )
A.(-∞,2) B.(-∞,2] C.(-2,2] D. (-2,2)
(2)[2020·黑龙江齐齐哈尔市第八中学高一检测]已知函数f(x)=mx2-mx-1,
对于任意的x∈[1,3],f(x)<-m+5恒成立,则m的取值范围是 .
C
解题归纳
一元二次不等式恒成立问题的解法
1.当未说明不等式为一元二次不等式时,应分二次项系数等于零和不等于零两种情况讨论.
2.一元二次不等式恒成立问题的常见类型:设y=ax2+bx+c(a≠0).
(1)y>0在x∈R上恒成立
(2)y<0在x∈R上恒成立
例5 某摩托车生产企业,上年度生产车的投入成本为1万元/辆,出厂价为1.2万元/辆,年销售量为1 000辆.本年度为适应市场需要,计划提高产品档次,适度增加投入成本,若每辆车投入成本增加的比例为x(0(1)写出本年度预计的年利润y与投入成本增加的比例x之间的关系式;
(2)为使本年度的利润比上年度有所增加,则投入成本增加的比例x应在什么范围内?
题组五 一元二次不等式的实际应用
解题归纳
用一元二次不等式求解实际应用题的一般步骤
1.审题:弄清题意,分析条件和结论,理顺数量关系;
2.建模:建立一元二次不等式模型;
3.求解:解一元二次不等式;
4.还原:把数学结论还原为实际问题.
巩固训练
解一元二次不等式的一般步骤:
第一步,将一元二次不等式化为一端为0的形式(习惯上二次项系数大于0).
第二步,求出相应一元二次方程的根,或判断出方程没有实根.
第三步,画出相应二次函数示意草图,方程有根的将根标在图中.
第四步,观察图象中位于x轴上方或下方的部分,对比不等式中不等号的方向,写出解集.
小结
Δ>0 Δ=0 Δ<0
y=ax2+bx+c(a>0) 的图象
ax2+bx+c=0(a>0) 的根 有两个不相等的实数根x1,x2(x1ax2+bx+c>0(a>0) 的解集 {x|xx2} R
ax2+bx+c<0(a>0) 的解集 {x|x1一元二次不等式的解集的求法
知易行难,重在行动
千里之行,始于足下
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
数学-RJ·A-必修第一册
2.3二次函数与一元二次方程、不等式
第二章 一元二次函数、方程和不等式
学习目标
1.经历从实际情境中抽象出一元二次不等式模型的过程.
2.通过函数图象了解一元二次不等式与相应函数、方程的联系.
3.会解一元二次不等式.
重点:从实际问题中抽象出一元二次不等式模型,围绕一元二次不等式的解法展开,突出体现数形结合思想.
难点:理解二次函数、一元二次方程与一元二次不等式的联系.
知识梳理
一个
2
一、一元二次不等式
1.一元二次不等式的概念
解集
二、二次函数的零点
一般地,对于二次函数y=ax2+bx+c,我们把使ax2+bx+c=0的实数x叫作二次函数y=ax2+bx+c的零点.
三、一元二次不等式与相应二次函数、二次方程的关系
例1 解不等式:(1)-3x2+6x-2>0;(2)4x2-4x+1≤0.
题组一 不含参数的一元二次不等式的解法
常考题型
(1)
(2)
解题归纳
解不含参数的一元二次不等式的步骤
1.通过对不等式的变形,使不等式右侧为0,使二次项系数为正.
2.对不等式左侧因式分解,若不易分解,则计算对应方程的判别式.
3.求出相应的一元二次方程的根或根据判别式说明方程有无实根.
4.根据一元二次方程根的情况画出对应的二次函数图象的草图.
5.根据图象写出不等式的解集.
记忆口诀:
设相应的二次函数的图象开口向上,并与x轴相交,则有口诀:大于取两边;小于取中间.
1. [2020·江苏南师附中高一检测]已知集合 U=R ,集合A={x|x2-3x+2>0},则UA=( )
A.(1,2) B.[1,2] C.(-2,-1) D.[ -2,-1]
2. “x2-3x+2<0”是“x<2”成立的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
B
A
巩固训练
题型二 简单分式不等式的解法
例2
解题归纳
1.若集合A=,B={x|-1
C.(-1,1) D.(-1,2)
2.不等式 ≤x-2的解集是 ( )
A.(-∞,0]∪(2,4] B.[0,2)∪[4,+∞)
C.[2,4) D.(-∞,2]∪(4,+∞)
B
C
巩固训练
例3 [2020·上海华东师范大学第一附属中学高二检测]解关于x的不等式ax2-2≥2x-ax(a∈R).
题组三 含参数的一元二次不等式的解法
【解题提示】 将原不等式化为(ax-2)(x+1)≥0,对参数a分5种情况讨论:a=0,a>0,-2
巩固训练
B
2.
解题归纳
解含参数的一元二次不等式的步骤
1.若二次项含有参数,应先讨论参数是等于0、小于0,还是大于0,然后整理不等式;
2.当二次项系数不为0时,讨论判别式与0的关系,判断方程的根的个数;
3.确定无根时可直接写出解集,确定方程有两个根时,要讨论两根的大小关系,从而确定解集的形式.
例4 若不等式(m+1)x2-(m-1)x+3(m-1)<0对任何实数x恒成立,求实数m的取值范围.
题组四 一元二次不等式的恒成立问题
巩固训练
(1) 对于任意实数x,不等式(a-2)x2- 2(a-2)x-4<0恒成立,则实数a的取值范围是( )
A.(-∞,2) B.(-∞,2] C.(-2,2] D. (-2,2)
(2)[2020·黑龙江齐齐哈尔市第八中学高一检测]已知函数f(x)=mx2-mx-1,
对于任意的x∈[1,3],f(x)<-m+5恒成立,则m的取值范围是 .
C
解题归纳
一元二次不等式恒成立问题的解法
1.当未说明不等式为一元二次不等式时,应分二次项系数等于零和不等于零两种情况讨论.
2.一元二次不等式恒成立问题的常见类型:设y=ax2+bx+c(a≠0).
(1)y>0在x∈R上恒成立
(2)y<0在x∈R上恒成立
例5 某摩托车生产企业,上年度生产车的投入成本为1万元/辆,出厂价为1.2万元/辆,年销售量为1 000辆.本年度为适应市场需要,计划提高产品档次,适度增加投入成本,若每辆车投入成本增加的比例为x(0
(2)为使本年度的利润比上年度有所增加,则投入成本增加的比例x应在什么范围内?
题组五 一元二次不等式的实际应用
解题归纳
用一元二次不等式求解实际应用题的一般步骤
1.审题:弄清题意,分析条件和结论,理顺数量关系;
2.建模:建立一元二次不等式模型;
3.求解:解一元二次不等式;
4.还原:把数学结论还原为实际问题.
巩固训练
解一元二次不等式的一般步骤:
第一步,将一元二次不等式化为一端为0的形式(习惯上二次项系数大于0).
第二步,求出相应一元二次方程的根,或判断出方程没有实根.
第三步,画出相应二次函数示意草图,方程有根的将根标在图中.
第四步,观察图象中位于x轴上方或下方的部分,对比不等式中不等号的方向,写出解集.
小结
Δ>0 Δ=0 Δ<0
y=ax2+bx+c(a>0) 的图象
ax2+bx+c=0(a>0) 的根 有两个不相等的实数根x1,x2(x1
ax2+bx+c<0(a>0) 的解集 {x|x1
知易行难,重在行动
千里之行,始于足下
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
