【课件】3.1.1 函数的概念 高中数学-RJA-必修第一册 (共43张PPT)
文档属性
| 名称 | 【课件】3.1.1 函数的概念 高中数学-RJA-必修第一册 (共43张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-18 16:58:16 | ||
图片预览










文档简介
(共43张PPT)
数学-RJ·A-必修第一册
3.1.1 函数的概念
第三章 函数的概念与性质
重点:体会函数是重要数学模型,正确理解函数的概念.
难点:对函数概念及符号()的理解.
1.体会函数是描述变量之间对应关系的重要数学模型,学会用集合与对应的语言来刻画函数,体会对应关系在刻画函数中的作用.
2.理解函数相等的概念,了解构成函数的三要素.
3.能正确使用函数、区间符号.
学习目标
知识梳理
一、函数的概念
函数的定义 设是非空的实数集,
如果对于集合中的任意一个数,
按照某种确定的对应关系,在集合中都有唯一确定的数和它对应,
那么就称为从集合A到集合的一个函数
函数的记法 =,
定义域 叫做自变量,的取值范围 叫做函数的定义域
值域 函数值的集合叫做函数的值域
集合A中元素的无剩余性
!
!
!
集合B中元素的可剩余性,
即集合B不一定是函数的值域,函数的值域一定是B的子集.
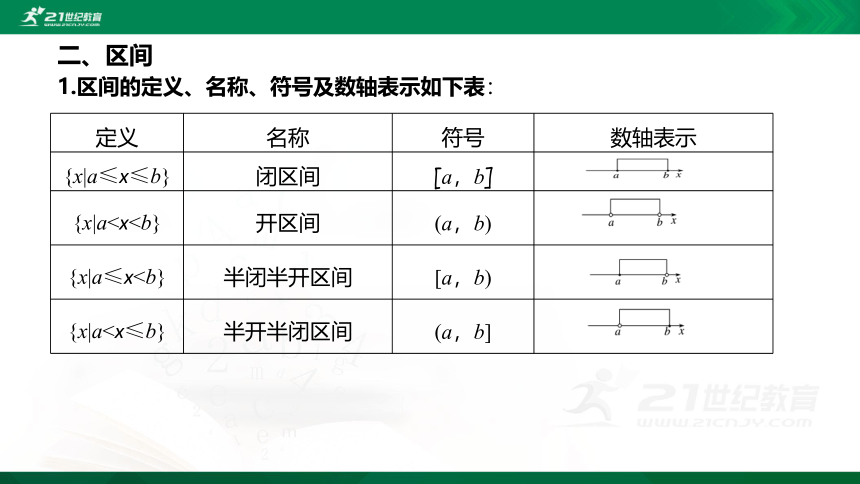
二、区间
1.区间的定义、名称、符号及数轴表示如下表:
定义 名称 符号 数轴表示
{x|a≤x≤b} 闭区间 [a,b]
{x|a{x|a≤x{x|a2.实数集 R 可以用区间表示为(- ∞,+ ∞),“∞”读作“无穷大”,“- ∞”读作“负无穷大”,“+ ∞”读作“正无穷大”.
定义 区间 数轴表示
{x|x≥a} [a,+∞)
{x|x>a} (a,+∞)
{x|x≤a} (-∞,a]
{x|xR (-∞,+∞) 取遍数轴上所有的值
三、同一个函数
一个函数的构成要素为:定义域,对应关系与值域.
因为值域是由定义域和对应关系决定的,所以,
如果两个函数的定义域相同,并且对应关系完全一致,我们就称这两个函数是同一个函数.
即相同的自变量对应的函数值也相同
!
一、函数关系的判断
常考题型
例1 下列从集合到集合的对应关系中,其中是函数的是( )
A.,对应关系,其中
B.,对应关系,其中
C.,对应关系,其中
D.,对应关系,其中
×
×
√
×
C
1.判断所给对应是否是函数
当集合M中的元素为奇数时,按照对应关系,其对应元素为非整数,但在N中无元素与之对应
M中每个元素,在N中都有两个不同元素对之对应
M中每个元素在N中都有唯一元素与之对应,故x→y是函数
反例:M中的元素0在N中没有元素对应
◆定义法判断函数关系
判断对应关系是否为函数,主要看以下三个方面:
1.A,B必须是非空数集;
2.A中任何一个元素在B中必须有元素与其对应;
3.A中任何一个元素在B中必须有唯一一个元素与其对应.
1.下列对应关系是否为A到B的函数.
(1)A=R,B=R,f:x→y=; (2)A=R+,B=R,f:x→y=±;
(3)A=N,B=N+,f:x→y=|x-1|;(4)A={x|0≤x≤3},B={x|0≤x≤1},f:x→y=x.
【解】(1)A中的元素-1在B中没有对应元素,故不是A到B的函数.
(2)对于集合A中任意一个正数,在集合B中有两个元素±与之对应,故不是A到B的函数.
(3)集合A中元素1在B中没有对应元素,故不是从A到B的函数.
(4)集合A中的任意一个元素,按照对应关系f:y=x,在集合B中都有唯一一个确定的实数x与之对应,故是从集合A到B的函数.
训练题
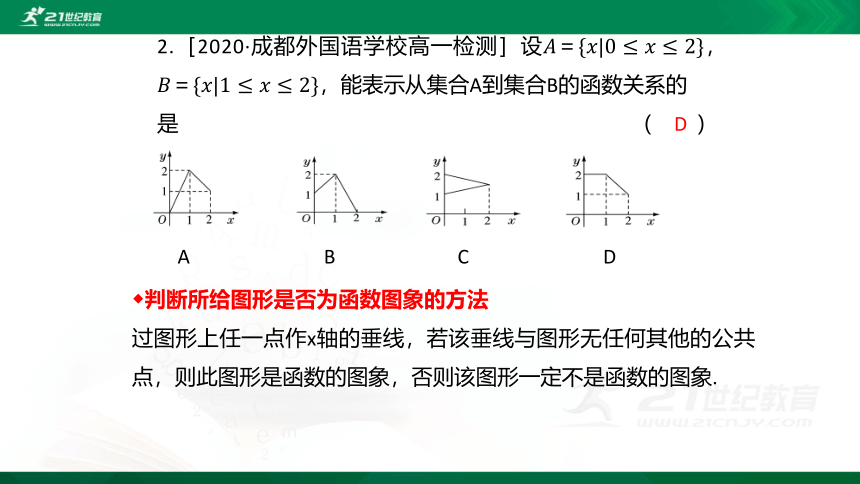
2.[2020·成都外国语学校高一检测]设,,能表示从集合A到集合B的函数关系的
是 ( )
A B C D
D
◆判断所给图形是否为函数图象的方法
过图形上任一点作x轴的垂线,若该垂线与图形无任何其他的公共点,则此图形是函数的图象,否则该图形一定不是函数的图象.
2.判断两个函数是否为同一函数
【解题提示】分析各选项中每组函数的定义域是否相同;定义域相同则再分析对应关系是否相同.两个条件都满足的是同一函数.
【答案】D
◆判断两个函数是否为同一函数的方法
只有当两个函数的定义域和对应关系都分别相同时,这两个函数才是同一函数.在具体判断时,(1)先看定义域,若定义域不同,则两函数不同;(2)再看值域,若值域不同,则两函数不同;(3)最后看对应关系,若不同,则不是同一函数.
D
训练题
B
【解析】要使函数有意义,则
解得且,
故函数的定义域为 , 故选B.
例3 [2020·重庆八中高一检测]函数(x)=的定义域为( )
A. B. C.R D.
二、函数的定义域
分母不为零
!
!
二次根号下代数式不小于零
1.已知解析式求定义域
【答案】B
◆已知的解析式,求的定义域的方法
(1)若为整式,则其定义域为实数集R.
(2)若是分式,则其定义域是使分母不等于0的实数的集合.
(3)若为偶次根式,则其定义域是使根号内的式子大于或等于0的实数的集合.
(4)若是由几部分数学式子构成的,则其定义域是使各部分数学式子都有意义的实数的集合,即交集.
(5)=的定义域是{∈R|≠0}.
1.函数+的定义域为( )
A. [-2, ) ∪(,+∞) B.[-2,+∞)
C. (-2, ) ∪(,+∞) D.(-2,+∞)
A
B
训练题
2.求抽象函数、复合函数的定义域
【解题提示】求出函数y=f(x)的定义域为[-1,3],然后解不等式-1≤3x-2≤3可得出函数y=f(3x-2)的定义域.
【答案】A
◆求复合函数定义域的方法
若函数的解析式是由几个部分的数学式子构成,则定义域是使各部分都有意义的实数的集合,即交集.其一般步骤为
1.将复合函数分解为若干个初等函数;
2.列出各初等函数满足的不等式;
3.各不等式组成的不等式组的解集即为复合函数的定义域.
C
B
C
【答案】D
◆已知函数定义域求参数的思路
求解此类问题需运用逆向思维以及化归与转化的思想方法.化归与转化即通过某种转化过程,将一个不易解决的问题转化为一个已经解决或比较容易解决的问题.
D
4.应用问题中函数的定义域
例6 如图3-1-1所示,有一块边长为a的正方形铁皮,将其四角各截去一个边长为x的小正方形,然后折成一个无盖的盒子,
写出此盒子的体积V以x为自变量的函数解析式,并指明
这个函数的定义域.
训练题
[2020·贵州遵义航天高级中学高一检测]将长度为2的一根铁丝折成一边长为x的矩形,矩形的面积y关于x的函数关系式是y=x(1-x),则函数的定义域为 ( )
A.R B.{x|x>0} C.{x|0D
三、求函数值或值域
1.已知解析式求函数值
◆求函数值的常用方法
1.求函数值问题,首先要确定函数的对应关系f的具体含义,再代入求值;
2.求类似f(g(x))的值,要注意f,g作用的对象,按“由内到外”的顺序求值;
3.求抽象函数值要恰当运用赋值法,针对所求的函数值,给予适当赋值.
训练题
[2019·江苏江阴四校高一联考]已知函数f(x)=x5+ax3+bx+1,
且f()=10,则f(2)= .
2.已知图象求函数值
例8 [2020·湖南长沙高一检测]已知函数y=f(x)的对应关系如下表,函数y=g(x)的图象是如图所示的曲线ABC,其中,,,则的值为 ( )
1 2 3
2 3 0
A.3 B.0 C.1 D.2
【解析】由图象可知g(2)=1,由表格可知f(1)=2,
∴ f(g(2))=f(1)=2.故选D.
【答案】D
训练题
[2020·北京西城区高一检测]如图,是函数的图象上的三点,其中,则的值为 ( )
A.0 B.1 C.2 D.3
B
3.求抽象函数的函数值
例9 [2020·山东沂水一中高一检测]若f(x)满足对任意的实数都有且,则+++…+ + + = ( )
A.1 009 B.2 018 C.2 019 D.2 020
【解析】利用==f(1)=2,累加可得.
因为f(x)满足对任意的实数a,b都有f(a+b)=f(a)·f(b)且f(1)=2,
所以==f(1)=2,
所以+++…+ + + = =2×1 010=2 020.
【答案】D
训练题
[2020·上海市上海中学高一检测]对任意正实数,,则= .
4.求函数的值域
例10 [2019·四川棠湖中学高一月考]函数y=x+的值域为()
A. B. C. D.
【解析】令t=,则t≥0,可得x=2-t2(t≥0),于是函数y=x+转化为f(t)=2-t2+t(t≥0), f(t)的图象开口向下,对称轴为直线t=.
∵ t≥0,∴ 当t=时,函数f(t)取得最大值为=,
∴ 函数f(t)的值域为.
∴ 函数y=x+的值域为.
【答案】C
◆求函数值域的常用方法
1.观察法:对于一些简单的函数,可通过定义域及对应关系用观察的方法来确定函数的值域.
2.配方法:对于含二次项的有关问题,常常根据问题的要求,采用配方法来解决.
3.判别式法:将函数视为关于自变量的一元二次方程,利用判别式求函数值的范围,常用于一些分式函数、无理函数等,使用此法要特别注意函数的定义域.
4.换元法:对于一些无理函数,常通过换元的方法将其化为有理函数,然后利用有理函数求值域的方法求出原函数的值域.
5.分离常数法:对于一些分子和分母都是关于自变量的一次式,常采用分离常数法求值域.
训练题
1.[2019·浙江丽水高一检测]函数f(x)=x2+2x(x∈[-2,1])的值域是 ( )
A.[0,3] B.[-1,3] C.[-1,0] D.[-1,+∞)
2.[2019·四川成都石室中学高一段考]函数y=的值域是 .
3.[2020·海南琼海市嘉积中学高一检测]若[x]表示不超过x的最大整数,例如[-2.3]=-3,[3.7]=3,那么函数f(x)=x-[x]的值域是 ( )
A.[0,1] B.(0,1) C.[0,1) D.(0,1]
B
C
5.已知函数值或值域求参数值
例11 [2019·四川宜宾三中高一月考]若函数y=的值域为[0,+∞),则实数m的取值范围是 ( )
A.(-,) B.[-,]
C.[-,+∞) D.(-∞,-]∪[,+∞)
【解析】∵ 函数y=的值域是[0,+∞),
∴ 2x2-mx+3能取遍所有大于或等于零的实数,
即方程2x2-mx+3=0在实数集范围内有解.
∴ Δ= m2-4×2×3=m2-24≥0,
解得m∈(-∞,-]∪[,+∞).
【答案】D
◆已知函数值或值域求参数值的方法
1.注意调整思维方向,根据值域的含义将给出的值域转化为方程的解或不等式的解集问题.
2.根据方程的解或不等式的解集情况来确定参数的值或取值范围.
训练题
1.[2019·四川阆中中学高一检测]若函数的定义域为[0,m],值域为[-10,-6],则m的取值范围是 ( )
A.[0,4] B.[4,6] C.[2,6] D.[2,4]
2.[2020·北京人大附中高一检测]函数,若存在,使得,则a的取值范围是 .
D
小结
三个知识点:
1.函数的概念(定义、记法、定义域、值域);2.区间(定义、符号、数轴表示);
3.同一函数(定义).
四种题型:
1.判断所给对应是否是函数;
2.已知()的解析式,求()的定义域;
3.已知函数关系式,求函数值;
4.判定两个函数是否为同一函数.
知易行难,重在行动
千里之行,始于足下
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
数学-RJ·A-必修第一册
3.1.1 函数的概念
第三章 函数的概念与性质
重点:体会函数是重要数学模型,正确理解函数的概念.
难点:对函数概念及符号()的理解.
1.体会函数是描述变量之间对应关系的重要数学模型,学会用集合与对应的语言来刻画函数,体会对应关系在刻画函数中的作用.
2.理解函数相等的概念,了解构成函数的三要素.
3.能正确使用函数、区间符号.
学习目标
知识梳理
一、函数的概念
函数的定义 设是非空的实数集,
如果对于集合中的任意一个数,
按照某种确定的对应关系,在集合中都有唯一确定的数和它对应,
那么就称为从集合A到集合的一个函数
函数的记法 =,
定义域 叫做自变量,的取值范围 叫做函数的定义域
值域 函数值的集合叫做函数的值域
集合A中元素的无剩余性
!
!
!
集合B中元素的可剩余性,
即集合B不一定是函数的值域,函数的值域一定是B的子集.
二、区间
1.区间的定义、名称、符号及数轴表示如下表:
定义 名称 符号 数轴表示
{x|a≤x≤b} 闭区间 [a,b]
{x|a
定义 区间 数轴表示
{x|x≥a} [a,+∞)
{x|x>a} (a,+∞)
{x|x≤a} (-∞,a]
{x|x
三、同一个函数
一个函数的构成要素为:定义域,对应关系与值域.
因为值域是由定义域和对应关系决定的,所以,
如果两个函数的定义域相同,并且对应关系完全一致,我们就称这两个函数是同一个函数.
即相同的自变量对应的函数值也相同
!
一、函数关系的判断
常考题型
例1 下列从集合到集合的对应关系中,其中是函数的是( )
A.,对应关系,其中
B.,对应关系,其中
C.,对应关系,其中
D.,对应关系,其中
×
×
√
×
C
1.判断所给对应是否是函数
当集合M中的元素为奇数时,按照对应关系,其对应元素为非整数,但在N中无元素与之对应
M中每个元素,在N中都有两个不同元素对之对应
M中每个元素在N中都有唯一元素与之对应,故x→y是函数
反例:M中的元素0在N中没有元素对应
◆定义法判断函数关系
判断对应关系是否为函数,主要看以下三个方面:
1.A,B必须是非空数集;
2.A中任何一个元素在B中必须有元素与其对应;
3.A中任何一个元素在B中必须有唯一一个元素与其对应.
1.下列对应关系是否为A到B的函数.
(1)A=R,B=R,f:x→y=; (2)A=R+,B=R,f:x→y=±;
(3)A=N,B=N+,f:x→y=|x-1|;(4)A={x|0≤x≤3},B={x|0≤x≤1},f:x→y=x.
【解】(1)A中的元素-1在B中没有对应元素,故不是A到B的函数.
(2)对于集合A中任意一个正数,在集合B中有两个元素±与之对应,故不是A到B的函数.
(3)集合A中元素1在B中没有对应元素,故不是从A到B的函数.
(4)集合A中的任意一个元素,按照对应关系f:y=x,在集合B中都有唯一一个确定的实数x与之对应,故是从集合A到B的函数.
训练题
2.[2020·成都外国语学校高一检测]设,,能表示从集合A到集合B的函数关系的
是 ( )
A B C D
D
◆判断所给图形是否为函数图象的方法
过图形上任一点作x轴的垂线,若该垂线与图形无任何其他的公共点,则此图形是函数的图象,否则该图形一定不是函数的图象.
2.判断两个函数是否为同一函数
【解题提示】分析各选项中每组函数的定义域是否相同;定义域相同则再分析对应关系是否相同.两个条件都满足的是同一函数.
【答案】D
◆判断两个函数是否为同一函数的方法
只有当两个函数的定义域和对应关系都分别相同时,这两个函数才是同一函数.在具体判断时,(1)先看定义域,若定义域不同,则两函数不同;(2)再看值域,若值域不同,则两函数不同;(3)最后看对应关系,若不同,则不是同一函数.
D
训练题
B
【解析】要使函数有意义,则
解得且,
故函数的定义域为 , 故选B.
例3 [2020·重庆八中高一检测]函数(x)=的定义域为( )
A. B. C.R D.
二、函数的定义域
分母不为零
!
!
二次根号下代数式不小于零
1.已知解析式求定义域
【答案】B
◆已知的解析式,求的定义域的方法
(1)若为整式,则其定义域为实数集R.
(2)若是分式,则其定义域是使分母不等于0的实数的集合.
(3)若为偶次根式,则其定义域是使根号内的式子大于或等于0的实数的集合.
(4)若是由几部分数学式子构成的,则其定义域是使各部分数学式子都有意义的实数的集合,即交集.
(5)=的定义域是{∈R|≠0}.
1.函数+的定义域为( )
A. [-2, ) ∪(,+∞) B.[-2,+∞)
C. (-2, ) ∪(,+∞) D.(-2,+∞)
A
B
训练题
2.求抽象函数、复合函数的定义域
【解题提示】求出函数y=f(x)的定义域为[-1,3],然后解不等式-1≤3x-2≤3可得出函数y=f(3x-2)的定义域.
【答案】A
◆求复合函数定义域的方法
若函数的解析式是由几个部分的数学式子构成,则定义域是使各部分都有意义的实数的集合,即交集.其一般步骤为
1.将复合函数分解为若干个初等函数;
2.列出各初等函数满足的不等式;
3.各不等式组成的不等式组的解集即为复合函数的定义域.
C
B
C
【答案】D
◆已知函数定义域求参数的思路
求解此类问题需运用逆向思维以及化归与转化的思想方法.化归与转化即通过某种转化过程,将一个不易解决的问题转化为一个已经解决或比较容易解决的问题.
D
4.应用问题中函数的定义域
例6 如图3-1-1所示,有一块边长为a的正方形铁皮,将其四角各截去一个边长为x的小正方形,然后折成一个无盖的盒子,
写出此盒子的体积V以x为自变量的函数解析式,并指明
这个函数的定义域.
训练题
[2020·贵州遵义航天高级中学高一检测]将长度为2的一根铁丝折成一边长为x的矩形,矩形的面积y关于x的函数关系式是y=x(1-x),则函数的定义域为 ( )
A.R B.{x|x>0} C.{x|0
三、求函数值或值域
1.已知解析式求函数值
◆求函数值的常用方法
1.求函数值问题,首先要确定函数的对应关系f的具体含义,再代入求值;
2.求类似f(g(x))的值,要注意f,g作用的对象,按“由内到外”的顺序求值;
3.求抽象函数值要恰当运用赋值法,针对所求的函数值,给予适当赋值.
训练题
[2019·江苏江阴四校高一联考]已知函数f(x)=x5+ax3+bx+1,
且f()=10,则f(2)= .
2.已知图象求函数值
例8 [2020·湖南长沙高一检测]已知函数y=f(x)的对应关系如下表,函数y=g(x)的图象是如图所示的曲线ABC,其中,,,则的值为 ( )
1 2 3
2 3 0
A.3 B.0 C.1 D.2
【解析】由图象可知g(2)=1,由表格可知f(1)=2,
∴ f(g(2))=f(1)=2.故选D.
【答案】D
训练题
[2020·北京西城区高一检测]如图,是函数的图象上的三点,其中,则的值为 ( )
A.0 B.1 C.2 D.3
B
3.求抽象函数的函数值
例9 [2020·山东沂水一中高一检测]若f(x)满足对任意的实数都有且,则+++…+ + + = ( )
A.1 009 B.2 018 C.2 019 D.2 020
【解析】利用==f(1)=2,累加可得.
因为f(x)满足对任意的实数a,b都有f(a+b)=f(a)·f(b)且f(1)=2,
所以==f(1)=2,
所以+++…+ + + = =2×1 010=2 020.
【答案】D
训练题
[2020·上海市上海中学高一检测]对任意正实数,,则= .
4.求函数的值域
例10 [2019·四川棠湖中学高一月考]函数y=x+的值域为()
A. B. C. D.
【解析】令t=,则t≥0,可得x=2-t2(t≥0),于是函数y=x+转化为f(t)=2-t2+t(t≥0), f(t)的图象开口向下,对称轴为直线t=.
∵ t≥0,∴ 当t=时,函数f(t)取得最大值为=,
∴ 函数f(t)的值域为.
∴ 函数y=x+的值域为.
【答案】C
◆求函数值域的常用方法
1.观察法:对于一些简单的函数,可通过定义域及对应关系用观察的方法来确定函数的值域.
2.配方法:对于含二次项的有关问题,常常根据问题的要求,采用配方法来解决.
3.判别式法:将函数视为关于自变量的一元二次方程,利用判别式求函数值的范围,常用于一些分式函数、无理函数等,使用此法要特别注意函数的定义域.
4.换元法:对于一些无理函数,常通过换元的方法将其化为有理函数,然后利用有理函数求值域的方法求出原函数的值域.
5.分离常数法:对于一些分子和分母都是关于自变量的一次式,常采用分离常数法求值域.
训练题
1.[2019·浙江丽水高一检测]函数f(x)=x2+2x(x∈[-2,1])的值域是 ( )
A.[0,3] B.[-1,3] C.[-1,0] D.[-1,+∞)
2.[2019·四川成都石室中学高一段考]函数y=的值域是 .
3.[2020·海南琼海市嘉积中学高一检测]若[x]表示不超过x的最大整数,例如[-2.3]=-3,[3.7]=3,那么函数f(x)=x-[x]的值域是 ( )
A.[0,1] B.(0,1) C.[0,1) D.(0,1]
B
C
5.已知函数值或值域求参数值
例11 [2019·四川宜宾三中高一月考]若函数y=的值域为[0,+∞),则实数m的取值范围是 ( )
A.(-,) B.[-,]
C.[-,+∞) D.(-∞,-]∪[,+∞)
【解析】∵ 函数y=的值域是[0,+∞),
∴ 2x2-mx+3能取遍所有大于或等于零的实数,
即方程2x2-mx+3=0在实数集范围内有解.
∴ Δ= m2-4×2×3=m2-24≥0,
解得m∈(-∞,-]∪[,+∞).
【答案】D
◆已知函数值或值域求参数值的方法
1.注意调整思维方向,根据值域的含义将给出的值域转化为方程的解或不等式的解集问题.
2.根据方程的解或不等式的解集情况来确定参数的值或取值范围.
训练题
1.[2019·四川阆中中学高一检测]若函数的定义域为[0,m],值域为[-10,-6],则m的取值范围是 ( )
A.[0,4] B.[4,6] C.[2,6] D.[2,4]
2.[2020·北京人大附中高一检测]函数,若存在,使得,则a的取值范围是 .
D
小结
三个知识点:
1.函数的概念(定义、记法、定义域、值域);2.区间(定义、符号、数轴表示);
3.同一函数(定义).
四种题型:
1.判断所给对应是否是函数;
2.已知()的解析式,求()的定义域;
3.已知函数关系式,求函数值;
4.判定两个函数是否为同一函数.
知易行难,重在行动
千里之行,始于足下
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
