【课件】3.1.2 函数的表示 高中数学-RJA-必修第一册(共47张PPT)
文档属性
| 名称 | 【课件】3.1.2 函数的表示 高中数学-RJA-必修第一册(共47张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 7.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-18 16:56:43 | ||
图片预览








文档简介
(共47张PPT)
数学-RJ·A-必修第一册
3.1.2 函数的表示法
第三章 函数的概念与性质
重点:会选择恰当的方法表示函数.
难点:函数的实际应用.
1.掌握函数的三种表示法:解析法、图象法、列表法,以及各种
表示法的优缺点.
2.在实际问题中,能够选择恰当的表示法来表示函数.
3.能利用函数图象求函数的值域,并确定函数值的变化趋势.
学习目标
知识梳理
函数的表示法
【总结归纳】
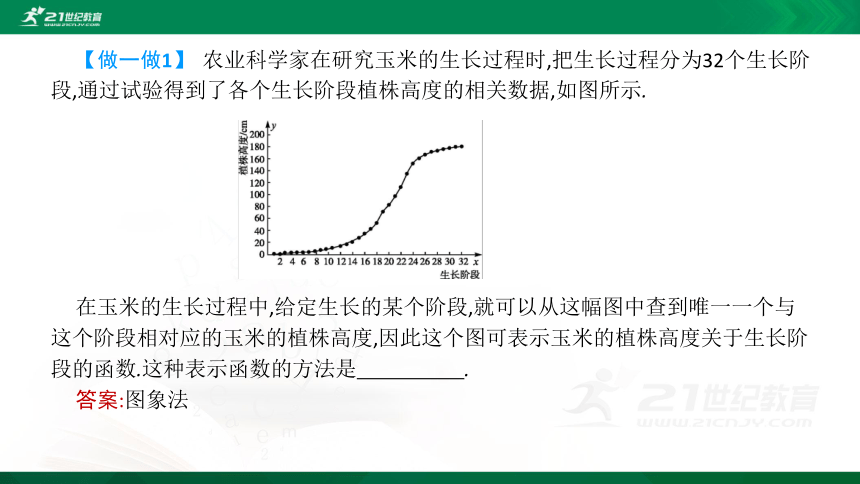
【做一做1】 农业科学家在研究玉米的生长过程时,把生长过程分为32个生长阶段,通过试验得到了各个生长阶段植株高度的相关数据,如图所示.
在玉米的生长过程中,给定生长的某个阶段,就可以从这幅图中查到唯一一个与这个阶段相对应的玉米的植株高度,因此这个图可表示玉米的植株高度关于生长阶段的函数.这种表示函数的方法是 .
答案:图象法
【做一做2】 用列表法将函数f(x)表示如下:
则f(f(2))= .
答案:0
0 1 2
4 2 0 1
一、函数的三种表示方法
常考题型
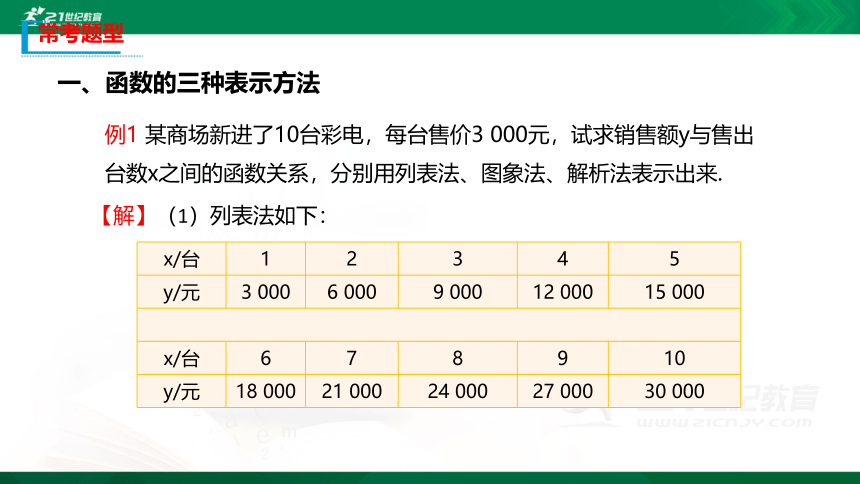
例1 某商场新进了10台彩电,每台售价3 000元,试求销售额y与售出台数x之间的函数关系,分别用列表法、图象法、解析法表示出来.
x/台 1 2 3 4 5
y/元 3 000 6 000 9 000 12 000 15 000
x/台 6 7 8 9 10
y/元 18 000 21 000 24 000 27 000 30 000
【解】(1)列表法如下:
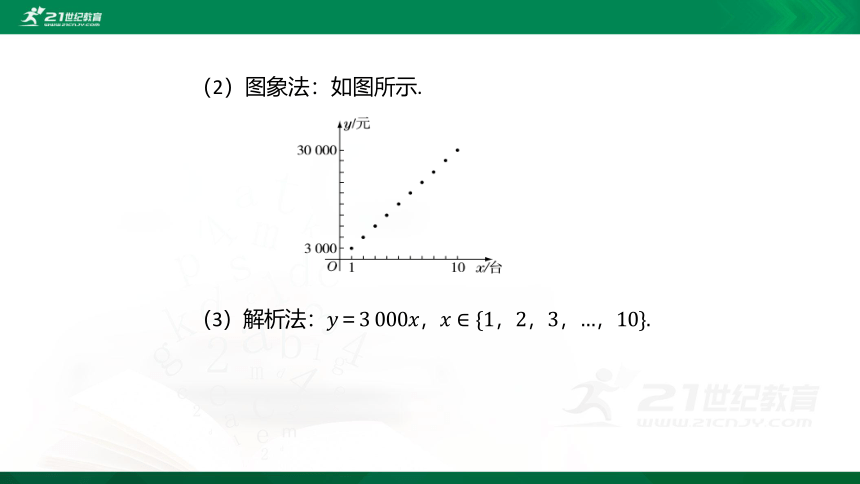
(2)图象法:如图所示.
(3)解析法:
◆函数三种表示方法及其特点
1.解析法、列表法、图象法均是函数的表示方法,解析法从“数”的方面简明、全面地概括了变量之间的数量关系;图象法从“形”的方面刻画了变量之间的数量关系;列表法,可根据表格由自变量x的取值查到和它对应的唯一的函数值y.
2.三种表示方法各有优缺点,并不是所有的函数都能用解析法表示,解题时要根据需要选择适当的表示方法,无论用哪种方法表示函数,都必须满足函数的概念.
训练题
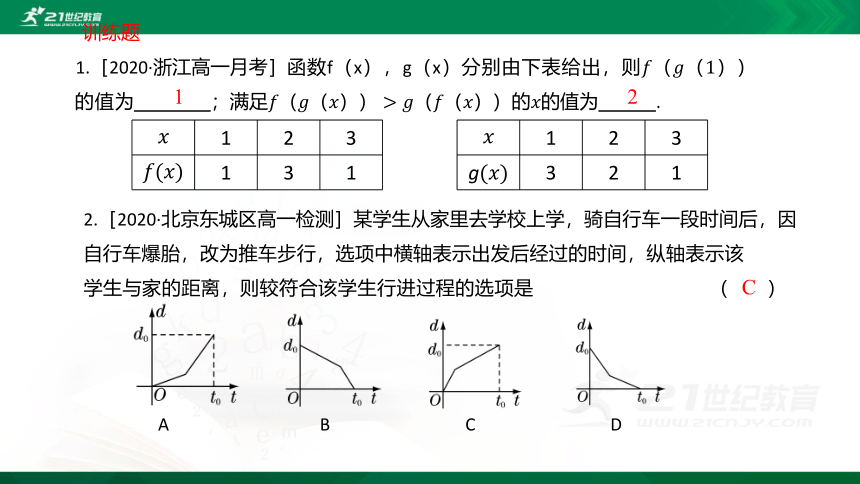
1.[2020·浙江高一月考]函数f(x),g(x)分别由下表给出,则
的值为 ;满足的的值为 .
1 2 3
1 3 1
1 2 3
g 3 2 1
2.[2020·北京东城区高一检测]某学生从家里去学校上学,骑自行车一段时间后,因自行车爆胎,改为推车步行,选项中横轴表示出发后经过的时间,纵轴表示该
学生与家的距离,则较符合该学生行进过程的选项是 ( )
A B C D
1
2
C
二、函数的解析式
1.已知函数类型求解析式
例2 [2019·海南高一检测]已知二次函数f(x)满足f(x+1)=
f(x)+2x,且f(0)=1.求f(x)的解析式.
◆待定系数法
1.如果已知函数类型,可设出函数解析式,再代入已知条件建立方程(组)求解,得到系数的值,从而使问题得以解决,这种方法叫做待定系数法.
2.待定系数法求函数解析式的两种类型:
(1)已知函数类型,满足两个解析式恒相等,要把两个解析式整理成相同的一般形式,由对应项系数相等求出待定系数,从而得解.
(2)解析式中的系数满足一些关系,利用这些关系列出方程(组),解方程(组)进而得解.
◆二次函数解析式的三种形式
1.一般式:f(x)=ax2+bx+c(a≠0);
2.顶点式:f(x)=a(x-m)2+n
(a≠0,(m,n)为顶点坐标);
3.两根式:f (x)=a (x-x1) (x-x2)(a≠0,x1,x2为方程f(x)=0的两个实根).
解题时要根据题设条件灵活选取.
训练题
1.[2019·宁夏石嘴山市第三中学高一月考]函数f(x)的图象如图所示,曲线BCD为抛物线的一部分,求f(x)的解析式.
2.[2019·辽师大附中高一检测]已知f(x)是图象对称轴为直线x=的二次函数,且f(0)=-1,f(1)=3.求f(x)的解析式.
2.已知f(g(x))求f(x)的解析式
例3 [2019·海南儋州市第一中学高一检测]已知f (+1)=x+,则f (x)的解析式是 ( )
f(x)=x2-1 B. f(x)=x2-1(x≥1)
C. f(x)=x2-4x-1(x≥1) D. f(x)=x2+1
【解析】(方法一)∵ (+1)2=x++1,∴ x+=(+1)2-1.
∴ f(+1)=(+1)2-1,其中+1≥1.∴ f(x)=x2-1(x≥1).
(方法二)令+1=t,则t≥1,x=(t-1)2,
∴ f(t)=(t-1)2+2(t-1)=t2-1,∴ f(x)=x2-1(x≥1).
【答案】B
◆ 代入法、配凑法与换元法
1.代入法:已知函数f(x)求函数f(g(x))的解析式,可用代入法;
2.配凑法:由已知条件f (g(x))=F(x),可将F(x)改写成关于g(x)的解析式,然后以x替代g(x),便得到f(x)的解析式,要注意此时f(x)的定义域为g(x)的值域.
3.换元法:对于形如y=f(g(x))的函数解析式,令t=g(x),从中求出x=φ(t),然后代入解析式求出f(t),再将t换成x,即可得到f(x)的解析式,换元后要注意新元的取值范围,如果新元t的取值范围不是全体实数,要标明所求函数的定义域.
A
C
【答案】f(x)=()
◆消元法(方程组法)
已知关于与或的关系式,可根据已知条件再构造出另外一个等式组成方程组,通过解方程组的方法求出的解析式.
训练题
1.[2020·黑龙江哈师大附中高一检测]已知函数满足,则= ( )
A. x2+x B.x2-3x C.x2+3x D.x2+3x
2.[2019·安徽合肥一六八中学高一检测]已知函数满足,则的值为 ( )
A. B. C. D.
B
D
4.求抽象函数的解析式
例5 函数f(x)对一切实数x,y均有
x(x+2y+1)成立,且f(1)=0,求f(x)的解析式.
【解】已知f(x+y)-f(y)=x(x+2y+1),
令x=1,y=0,得f(1)-f(0)=2.
∵ f(1)=0,∴ f(0)=-2.
再令y=0,得f(x)-f(0)=x(x+1),
∴ f(x)+2=x2+x,即f(x)=x2+x-2.
◆赋值法求抽象函数的解析式
已知所给函数方程中含有两个变量时,可对这两个变量交替用特殊值代入,或使这两个变量相等代入,再利用条件求出未知的函数.至于赋予何值则需依据题目特征而定.
训练题
[2020·黑龙江哈尔滨高一检测]若函数f(x)对定义域内任意两个自变量x,y都有f(x+y)=f(x)f(y),则f(x)可以是 ( )
A. f(x)=2x+1 B. f(x)=x2 C. f(x)= D. f(x)=
D
【解】(1)由已知函数定义域为{0,1,2},列表如下:
其图象是离散的点列,如图所示,值域为{1,3,5}.
例6 作出下列函数的图象并求出其值域.
(1)y=2x+1,x∈Z且0≤x≤2;(2)y= ,x∈[2,+∞);
(3)y=x2+2x,x∈[-2,2].
三、函数的图象问题
x 0 1 2
y 1 3 5
1.图象的画法
(2)由已知函数定义域为[2,+∞),列表如下:
其图象是反比例函数y= 图象的一部分,如图所示,
观察图象知函数值域为(0,1].
x 2 3 4 5 …
y 1 …
(3)由已知函数定义域为[-2,2],列表如下:
其图象是抛物线y=x2+2x在-2≤x≤2之间的部分,如图所示,
由图象可得函数的值域是[-1,8].
x -2 -1 0 1 2
y 0 -1 0 3 8
◆描点法作图的步骤
训练题 作出下列函数的图象:
(1)y=;(2)y=|x2-2x|+1.
【解】(1)∵ y==2+,∴ 先作函数y= 的图象,把它向右平移1个单位长度得到函数y=的图象,再把平移后的图象向上平移2个单位长度得到函数y=的图象,如图所示.
(2)先作函数y=x2-2x的图象,保留x轴上方的图象,再把x轴下方图象对称翻到x轴上方,最后把图象整体向上平移1个单位长度,即得到y=|x2-2x|+1的图象,如图所示.
◆作函数图象六注意
1.先确定函数的定义域,要在定义域内作图;
2.图象是实线或实点,定义域外的部分有时可用虚线来衬托整个图象;
3.要标出某些关键点,例如图象的顶点、端点、与坐标轴的交点;
4.作分段函数的图象时,应根据不同取值范围上的解析式分别作出;
5.函数图象可以是连续的曲线,也可以是直线、折线、离散的点等;
6.对于已经熟悉形状的函数图象,只需选出几个特殊点即可作出全图,其中抛物线选3个点即可,直线或线段选2个点即可.
2.图象的识别
例7 [2020·江西南昌市实验中学高一月考]在函数,
的图象上有一点P(t,|t|),此函数图象
与x轴、直线x=-1及x=t围成图形(如图阴影部分)的面积
为S,则S与t的函数关系可表示为 ( )
A B C D
【答案】B
训练题
1.[2020·北京人大附中高一检测]如图3-1-10所示,是吴老师散步时所走的离家距离(y)与行走时间(x)之间的函数关系的图象,若用黑点表示吴老师家的位置,则吴老师散步行走的路线可能是 ( )
A B C D
2.[2019·山东菏泽高一检测]已知a≠0,b>0,一次函数y=ax+b,二次函数
y=ax2,则下列图象中可以成立的是 ( )
A B C D
D
B
◆根据函数解析式选择对应图象的方法
求解此类问题,首先要从函数解析式中得到函数的一些基本性质、特征;然后从图象中读出有用的信息,根据这些信息排除不符合的选项.
3.图象的应用
例8 对于任意的实数表示中较小的那个数.
若f(x)=2-x2,g(x)=x,则min{ f(x),g(x)}的最大值是 .
【答案】1
B
2
四、分段函数问题
【解题提示】(1)已知x0,求f(x0).求解时首先要分清x0所在的范围,然后选择相应的解析式代入即可.(2)已知f(x0)=t,求x0.求解时要先对不同的范围进行分类讨论,分别求出x0,并验证求得的x0是否满足要求,最后得出结果.
【答案】
◆分段函数求值的求解策略
分段函数的求值问题,要根据自变量的范围选择适当的解析式去求函数值.若不确定,则需要分类讨论.若知道分段函数的函数值,则应分类讨论求出不同范围上的自变量的值,并且要检验所求得的值是否符合相应各段上自变量的取值范围,也可以先画出分段函数的图象,结合图象求函数值或相应的自变量的值.
A
C
B
A
【解题提示】(1)根据分段函数的表达式,利用代入法进行求解即可;(2)根据分段函数的表达式,讨论x的取值范围,分别列不等式进行求解,然后求并集即可.
【解】(1)f(2)=-2×2+8=-4+8=4,
f(f(-1))=f(4)=-2×4+8=0.
(2)若x≤1,由f(x)≥4得x+5≥4,即x≥-1,此时-1≤x≤1.
若x>1,由f (x)≥4得-2x+8≥4,即x≤2,此时1综上,-1≤x≤2.
【点评】
(1)求分段函数的函数值,要先确定要求值的自变量属于哪一段区间,然后代入该段的解析式求值,当出现f(f(a))的形式时,应从内到外依次求值.
(2)当给出函数值求自变量的值时,先假设所求的值在分段函数定义区间的各段上,然后求出相应自变量的值,切记要代入检验,看所求的自变量的值是否满足相应段自变量的取值范围.
C
[0,2)
◆已知分段函数的函数值求参数的方法
1.对参数的取值范围分类讨论;
2.代入到不同的解析式中;
3.通过解不等式求出参数的取值范围;
4.检验所求得的取值范围是否在讨论的区间之内.
小结
一个知识点:
函数的表示方法(图像法、解析法、列表法)
四种题型:
1.函数的三种表示方法;
2.函数图象的画法;
3.图象的识别;
4.与分段函数有关的实际问题.
知易行难,重在行动
千里之行,始于足下
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
数学-RJ·A-必修第一册
3.1.2 函数的表示法
第三章 函数的概念与性质
重点:会选择恰当的方法表示函数.
难点:函数的实际应用.
1.掌握函数的三种表示法:解析法、图象法、列表法,以及各种
表示法的优缺点.
2.在实际问题中,能够选择恰当的表示法来表示函数.
3.能利用函数图象求函数的值域,并确定函数值的变化趋势.
学习目标
知识梳理
函数的表示法
【总结归纳】
【做一做1】 农业科学家在研究玉米的生长过程时,把生长过程分为32个生长阶段,通过试验得到了各个生长阶段植株高度的相关数据,如图所示.
在玉米的生长过程中,给定生长的某个阶段,就可以从这幅图中查到唯一一个与这个阶段相对应的玉米的植株高度,因此这个图可表示玉米的植株高度关于生长阶段的函数.这种表示函数的方法是 .
答案:图象法
【做一做2】 用列表法将函数f(x)表示如下:
则f(f(2))= .
答案:0
0 1 2
4 2 0 1
一、函数的三种表示方法
常考题型
例1 某商场新进了10台彩电,每台售价3 000元,试求销售额y与售出台数x之间的函数关系,分别用列表法、图象法、解析法表示出来.
x/台 1 2 3 4 5
y/元 3 000 6 000 9 000 12 000 15 000
x/台 6 7 8 9 10
y/元 18 000 21 000 24 000 27 000 30 000
【解】(1)列表法如下:
(2)图象法:如图所示.
(3)解析法:
◆函数三种表示方法及其特点
1.解析法、列表法、图象法均是函数的表示方法,解析法从“数”的方面简明、全面地概括了变量之间的数量关系;图象法从“形”的方面刻画了变量之间的数量关系;列表法,可根据表格由自变量x的取值查到和它对应的唯一的函数值y.
2.三种表示方法各有优缺点,并不是所有的函数都能用解析法表示,解题时要根据需要选择适当的表示方法,无论用哪种方法表示函数,都必须满足函数的概念.
训练题
1.[2020·浙江高一月考]函数f(x),g(x)分别由下表给出,则
的值为 ;满足的的值为 .
1 2 3
1 3 1
1 2 3
g 3 2 1
2.[2020·北京东城区高一检测]某学生从家里去学校上学,骑自行车一段时间后,因自行车爆胎,改为推车步行,选项中横轴表示出发后经过的时间,纵轴表示该
学生与家的距离,则较符合该学生行进过程的选项是 ( )
A B C D
1
2
C
二、函数的解析式
1.已知函数类型求解析式
例2 [2019·海南高一检测]已知二次函数f(x)满足f(x+1)=
f(x)+2x,且f(0)=1.求f(x)的解析式.
◆待定系数法
1.如果已知函数类型,可设出函数解析式,再代入已知条件建立方程(组)求解,得到系数的值,从而使问题得以解决,这种方法叫做待定系数法.
2.待定系数法求函数解析式的两种类型:
(1)已知函数类型,满足两个解析式恒相等,要把两个解析式整理成相同的一般形式,由对应项系数相等求出待定系数,从而得解.
(2)解析式中的系数满足一些关系,利用这些关系列出方程(组),解方程(组)进而得解.
◆二次函数解析式的三种形式
1.一般式:f(x)=ax2+bx+c(a≠0);
2.顶点式:f(x)=a(x-m)2+n
(a≠0,(m,n)为顶点坐标);
3.两根式:f (x)=a (x-x1) (x-x2)(a≠0,x1,x2为方程f(x)=0的两个实根).
解题时要根据题设条件灵活选取.
训练题
1.[2019·宁夏石嘴山市第三中学高一月考]函数f(x)的图象如图所示,曲线BCD为抛物线的一部分,求f(x)的解析式.
2.[2019·辽师大附中高一检测]已知f(x)是图象对称轴为直线x=的二次函数,且f(0)=-1,f(1)=3.求f(x)的解析式.
2.已知f(g(x))求f(x)的解析式
例3 [2019·海南儋州市第一中学高一检测]已知f (+1)=x+,则f (x)的解析式是 ( )
f(x)=x2-1 B. f(x)=x2-1(x≥1)
C. f(x)=x2-4x-1(x≥1) D. f(x)=x2+1
【解析】(方法一)∵ (+1)2=x++1,∴ x+=(+1)2-1.
∴ f(+1)=(+1)2-1,其中+1≥1.∴ f(x)=x2-1(x≥1).
(方法二)令+1=t,则t≥1,x=(t-1)2,
∴ f(t)=(t-1)2+2(t-1)=t2-1,∴ f(x)=x2-1(x≥1).
【答案】B
◆ 代入法、配凑法与换元法
1.代入法:已知函数f(x)求函数f(g(x))的解析式,可用代入法;
2.配凑法:由已知条件f (g(x))=F(x),可将F(x)改写成关于g(x)的解析式,然后以x替代g(x),便得到f(x)的解析式,要注意此时f(x)的定义域为g(x)的值域.
3.换元法:对于形如y=f(g(x))的函数解析式,令t=g(x),从中求出x=φ(t),然后代入解析式求出f(t),再将t换成x,即可得到f(x)的解析式,换元后要注意新元的取值范围,如果新元t的取值范围不是全体实数,要标明所求函数的定义域.
A
C
【答案】f(x)=()
◆消元法(方程组法)
已知关于与或的关系式,可根据已知条件再构造出另外一个等式组成方程组,通过解方程组的方法求出的解析式.
训练题
1.[2020·黑龙江哈师大附中高一检测]已知函数满足,则= ( )
A. x2+x B.x2-3x C.x2+3x D.x2+3x
2.[2019·安徽合肥一六八中学高一检测]已知函数满足,则的值为 ( )
A. B. C. D.
B
D
4.求抽象函数的解析式
例5 函数f(x)对一切实数x,y均有
x(x+2y+1)成立,且f(1)=0,求f(x)的解析式.
【解】已知f(x+y)-f(y)=x(x+2y+1),
令x=1,y=0,得f(1)-f(0)=2.
∵ f(1)=0,∴ f(0)=-2.
再令y=0,得f(x)-f(0)=x(x+1),
∴ f(x)+2=x2+x,即f(x)=x2+x-2.
◆赋值法求抽象函数的解析式
已知所给函数方程中含有两个变量时,可对这两个变量交替用特殊值代入,或使这两个变量相等代入,再利用条件求出未知的函数.至于赋予何值则需依据题目特征而定.
训练题
[2020·黑龙江哈尔滨高一检测]若函数f(x)对定义域内任意两个自变量x,y都有f(x+y)=f(x)f(y),则f(x)可以是 ( )
A. f(x)=2x+1 B. f(x)=x2 C. f(x)= D. f(x)=
D
【解】(1)由已知函数定义域为{0,1,2},列表如下:
其图象是离散的点列,如图所示,值域为{1,3,5}.
例6 作出下列函数的图象并求出其值域.
(1)y=2x+1,x∈Z且0≤x≤2;(2)y= ,x∈[2,+∞);
(3)y=x2+2x,x∈[-2,2].
三、函数的图象问题
x 0 1 2
y 1 3 5
1.图象的画法
(2)由已知函数定义域为[2,+∞),列表如下:
其图象是反比例函数y= 图象的一部分,如图所示,
观察图象知函数值域为(0,1].
x 2 3 4 5 …
y 1 …
(3)由已知函数定义域为[-2,2],列表如下:
其图象是抛物线y=x2+2x在-2≤x≤2之间的部分,如图所示,
由图象可得函数的值域是[-1,8].
x -2 -1 0 1 2
y 0 -1 0 3 8
◆描点法作图的步骤
训练题 作出下列函数的图象:
(1)y=;(2)y=|x2-2x|+1.
【解】(1)∵ y==2+,∴ 先作函数y= 的图象,把它向右平移1个单位长度得到函数y=的图象,再把平移后的图象向上平移2个单位长度得到函数y=的图象,如图所示.
(2)先作函数y=x2-2x的图象,保留x轴上方的图象,再把x轴下方图象对称翻到x轴上方,最后把图象整体向上平移1个单位长度,即得到y=|x2-2x|+1的图象,如图所示.
◆作函数图象六注意
1.先确定函数的定义域,要在定义域内作图;
2.图象是实线或实点,定义域外的部分有时可用虚线来衬托整个图象;
3.要标出某些关键点,例如图象的顶点、端点、与坐标轴的交点;
4.作分段函数的图象时,应根据不同取值范围上的解析式分别作出;
5.函数图象可以是连续的曲线,也可以是直线、折线、离散的点等;
6.对于已经熟悉形状的函数图象,只需选出几个特殊点即可作出全图,其中抛物线选3个点即可,直线或线段选2个点即可.
2.图象的识别
例7 [2020·江西南昌市实验中学高一月考]在函数,
的图象上有一点P(t,|t|),此函数图象
与x轴、直线x=-1及x=t围成图形(如图阴影部分)的面积
为S,则S与t的函数关系可表示为 ( )
A B C D
【答案】B
训练题
1.[2020·北京人大附中高一检测]如图3-1-10所示,是吴老师散步时所走的离家距离(y)与行走时间(x)之间的函数关系的图象,若用黑点表示吴老师家的位置,则吴老师散步行走的路线可能是 ( )
A B C D
2.[2019·山东菏泽高一检测]已知a≠0,b>0,一次函数y=ax+b,二次函数
y=ax2,则下列图象中可以成立的是 ( )
A B C D
D
B
◆根据函数解析式选择对应图象的方法
求解此类问题,首先要从函数解析式中得到函数的一些基本性质、特征;然后从图象中读出有用的信息,根据这些信息排除不符合的选项.
3.图象的应用
例8 对于任意的实数表示中较小的那个数.
若f(x)=2-x2,g(x)=x,则min{ f(x),g(x)}的最大值是 .
【答案】1
B
2
四、分段函数问题
【解题提示】(1)已知x0,求f(x0).求解时首先要分清x0所在的范围,然后选择相应的解析式代入即可.(2)已知f(x0)=t,求x0.求解时要先对不同的范围进行分类讨论,分别求出x0,并验证求得的x0是否满足要求,最后得出结果.
【答案】
◆分段函数求值的求解策略
分段函数的求值问题,要根据自变量的范围选择适当的解析式去求函数值.若不确定,则需要分类讨论.若知道分段函数的函数值,则应分类讨论求出不同范围上的自变量的值,并且要检验所求得的值是否符合相应各段上自变量的取值范围,也可以先画出分段函数的图象,结合图象求函数值或相应的自变量的值.
A
C
B
A
【解题提示】(1)根据分段函数的表达式,利用代入法进行求解即可;(2)根据分段函数的表达式,讨论x的取值范围,分别列不等式进行求解,然后求并集即可.
【解】(1)f(2)=-2×2+8=-4+8=4,
f(f(-1))=f(4)=-2×4+8=0.
(2)若x≤1,由f(x)≥4得x+5≥4,即x≥-1,此时-1≤x≤1.
若x>1,由f (x)≥4得-2x+8≥4,即x≤2,此时1
【点评】
(1)求分段函数的函数值,要先确定要求值的自变量属于哪一段区间,然后代入该段的解析式求值,当出现f(f(a))的形式时,应从内到外依次求值.
(2)当给出函数值求自变量的值时,先假设所求的值在分段函数定义区间的各段上,然后求出相应自变量的值,切记要代入检验,看所求的自变量的值是否满足相应段自变量的取值范围.
C
[0,2)
◆已知分段函数的函数值求参数的方法
1.对参数的取值范围分类讨论;
2.代入到不同的解析式中;
3.通过解不等式求出参数的取值范围;
4.检验所求得的取值范围是否在讨论的区间之内.
小结
一个知识点:
函数的表示方法(图像法、解析法、列表法)
四种题型:
1.函数的三种表示方法;
2.函数图象的画法;
3.图象的识别;
4.与分段函数有关的实际问题.
知易行难,重在行动
千里之行,始于足下
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
