【课件】3.2.1 单调性与最大(小)值-第1课时 高中数学-RJA-必修第一册 (共48张PPT)
文档属性
| 名称 | 【课件】3.2.1 单调性与最大(小)值-第1课时 高中数学-RJA-必修第一册 (共48张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-19 18:24:07 | ||
图片预览










文档简介
(共48张PPT)
数学-RJ·A-必修第一册
3.2.1 单调性与最大(小)值
第1课时
第三章 函数的概念与性质
重点:理解函数单调性的概念;判断函数的单调性.
难点:判断函数的单调性.
1.了解函数的单调区间、单调性等概念.
2.会划分函数的单调区间,判断单调性.
3.会用定义证明函数的单调性.
学习目标
知识梳理
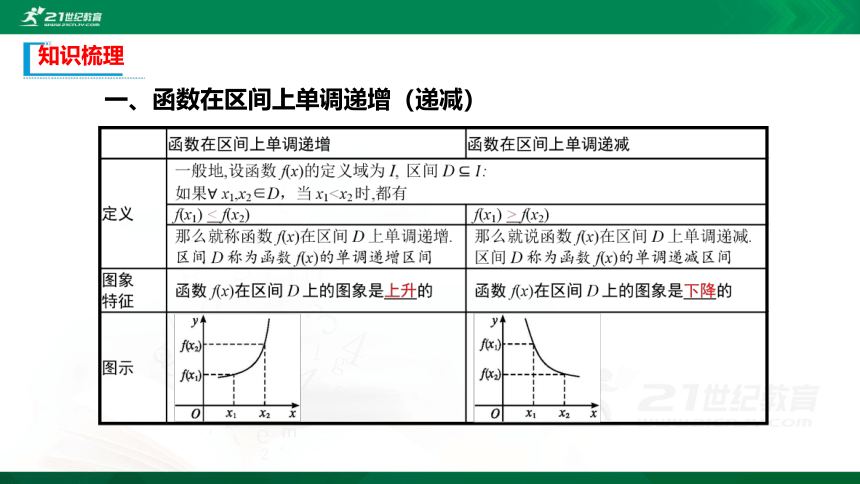
一、函数在区间上单调递增(递减)
总结归纳
1.函数f(x)在区间D上是增函数,x1,x2∈D,且x1≠x2
(x1-x2)[f(x1)-f(x2)]>0
2.函数f(x)在区间D上是减函数,x1,x2∈D,且x1≠x2
(x1-x2)[f(x1)-f(x2)]<0
特别提醒
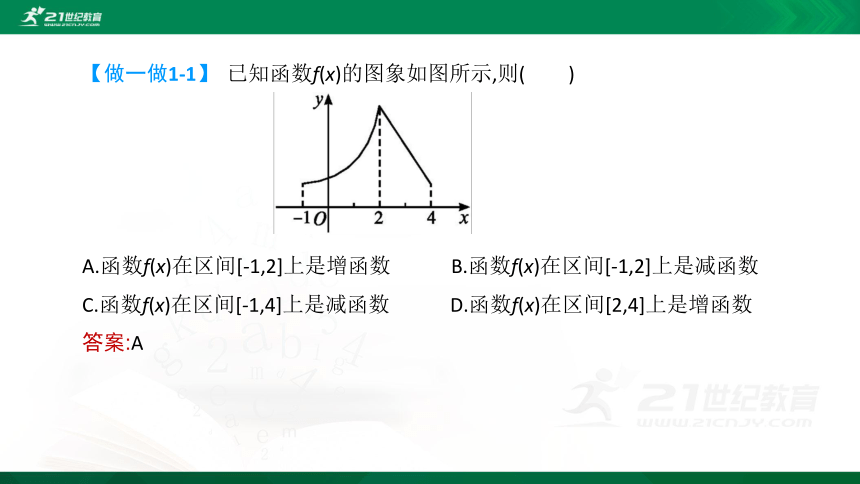
函数在区间上单调递增(递减)的定义是用数学符号来刻画函数的图象特征,它反映了函数图象的变化趋势(当自变量增大时,函数值是增大还是减小,图象是上升还是下降);函数y=f(x)在区间D上是单调递增(递减),等价于对于D中任意的两个自变量x1,x2,且x1f(x2));其中“任意”二字是关键,不能用具体的两个自变量代替,否则就会产生错误.比如函数f(x)取x1=-1,x2=1,f(x1)=-1,f(x2)=1,f(x1)【做一做1-1】 已知函数f(x)的图象如图所示,则( )
A.函数f(x)在区间[-1,2]上是增函数 B.函数f(x)在区间[-1,2]上是减函数
C.函数f(x)在区间[-1,4]上是减函数 D.函数f(x)在区间[2,4]上是增函数
答案:A
【做一做1-2】 已知函数y=f(x)在区间(a,b)内是单调递减,x1,x2∈(a,b),且x1A.f(x1)f(x2)
C.f(x1)=f(x2) D.以上都有可能
答案:B
二、函数的增减性
1.定义:如果函数y=f(x)在区间D上单调递增或单调递减,那么就说函数y=f(x)在这一区间具有(严格的)单调性,区间D叫做y=f(x)的单调区间.
2.图象特征:函数y=f(x)在区间D上具有单调性,则函数y=f(x)在区间D上的图象是上升的或下降的.
总结归纳
基本初等函数的单调区间如下表所示:
【做一做2】已知[0,3]是函数f(x)定义域内的一个区间,若f(1)A.是单调递增 B.是单调递减
C.不单调递增就是单调递减 D.增减性不能确定
解析:虽然1,2∈[0,3],1<2,且f(1)答案:D
常考题型
一、用定义法判断和证明函数的单调性
◆用定义法证明函数的单调性的一般步骤
(1)取值,设x1,x2是给定区间内的任意两个值,且x1(2)作差变形,作差f(x1)-f(x2)(或f(x2)-f(x1)),通过因式分解、配方、通分、有理化等方法使其转化为易于判断正负的式子.
(3)判号,确定f(x1)-f(x2)(或f(x2)- f(x1))的符号,当符号不确定时,要进行分类讨论.
(4)定论,根据定义得出结论.
◆用定义法证明函数的单调性常用的变形技巧
1.因式分解:当原函数是多项式函数时,通常作差后进行因式分解.
2.通分:当原函数是分式函数时,作差后往往先进行通分,然后对分子进行因式分解.
3.配方:当原函数是二次函数时,作差后可以考虑配方.
4.分子有理化:当原函数是根式函数时,作差后往往考虑分子有理化.
二、函数单调性的判断及单调区间的求解
◆含参函数单调性的两种类型及解法
1.作差变形后式子的符号与参数值无关,直接用定义判断.
2.作差变形后式子的符号与参数值有关,此时应对参数分类讨论.
C
2.图象法
例3 函数f(x)=|x-2|x的单调减区间是 ( )
A.[1,2] B.[-1,0]
C.[0,2] D.[2,+∞)
【答案】A
训练题
1.[2019·湖南衡阳市一中高一月考]函数y=|x2-3x-4|的单调
增区间是 .
,[4,+∞)
2.已知函数f(x)=-x2+2|x|+3.
(1)用分段函数的形式表示f(x); (2)画出f(x)的图象;
(3)根据图象写出f(x)的单调区间.
解:(1)当x≥0时,f(x)=-x2+2x+3=-(x-1)2+4;
当x<0时,f(x)=-x2-2x+3=-(x+1)2+4,
即f(x)
(2)函数f(x)的图象如图所示.
(3)函数f(x)的图象在区间(-∞,-1]和[0,1]上是上升的,
在区间(-1,0)和(1,+∞)内是下降的,
所以f(x)的单调递增区间是(-∞,-1],[0,1],单调递减区间是[-1,0],[1,+∞).
◆图象法
适用于已知函数图象或函数图象可以作出的函数.
图象法就是先画出函数的图象,然后利用图象直观判断函数的单调性.从左到右图象逐渐上升就是单调递增,逐渐下降就是单调递减.
f(x) g(x) f(x)+ g(x) f(x)-
g(x)
增 增 增 不确定
增 减 不确定 增
减 减 减 不确定
减 增 不确定 减
训练题
1.[2019·安徽芜湖高一月考]函数f(x)=1- ( )
A.在(-1,+∞)上单调递增 B.在(1,+∞)上单调递增
C.在(-1,+∞)上单调递减 D.在(1,+∞)上单调递减
B
2.[2020·上海市育才中学高一月考]已知函数f(x)=x2,x∈[1,+∞),判断该函数的单调性,并证明.
【解题提示】设t=x2+3x-4,由t≥0,可得x≤-4或x≥1,则运用复合函数的单调性(同增异减),以及二次函数和幂函数的单调性,即可得到所求的单调区间.
【答案】[1,+∞)
◆判断复合函数的单调性的方法
1.对于复合函数y=f(g(x)),如果u=g(x)在(a,b)上是单调函数,
并且y=f(u)在(g(a),g(b))或者(g(b),g(a))上也是单调
函数,则y=f(g(x))在(a,b)上的单调性如下表所示:
u=g(x) y=f(u) y=f(g(x))
增 增 增
增 减 减
减 增 减
减 减 增
简记为“同增异减”.
2.若一个函数是由多个简单函数复合而成的,则此复合函数的单调性由简单函数中减函数的个数决定.若减函数有偶数个,则这个复合函数为增函数;若减函数有奇数个,则这个复合函数为减函数.
(-∞,0) 和[1,+∞)
(0,1]
5.抽象函数的单调性
例6[2020·安徽庐江二中高一检测]已知函数f(x)对任意的a,b∈,都有f(a+b)=f(a)+f(b)-1,并且当x>0时,f(x)>1.
(1)求证:f(x)是R上的增函数;
(2)若f(4)=5,解不等式f(3m2-m-2)<3.
(1)【证明】任取x1,x2∈R,且x10,∴ f(x2-x1)>1,
∴ f(x2)-f(x1)=f((x2-x1)+x1)-f(x1)
=f(x2-x1)+f(x1)-1-f(x1)=f(x2-x1)-1>0,∴ f(x1)∴ f(x)是R上的增函数.
◆判断抽象函数的单调性的方法
1.抽象函数的单调性一般用定义法来判断,其一般步骤为
(1)在所证区间上设出x1,x2(x1(2)利用题设条件向已知区间转化得出函数值之间的大小关系
(f(x1)f(x2)).
(3)由定义得出结论.
训练题 [2019·河南南阳高一检测]已知定义在上的函数对任意x,y∈(0,+∞),恒有f(xy)=f(x)+f(y),且当00,判断f(x)在(0,+∞)上的单调性并加以证明.
三、函数单调性的应用
1.利用函数的单调性比较大小
例7 [2020·陕西西电附中高一月考]若函数f(x)的定义域为R,且在(0,+∞)上单调递减,则下列不等式成立的是 ( )
A.>f(a2-a+1) B.≥f(a2-a+1) C.【解题提示】判断与a2-a+1的大小关系,利用函数的单调性,即可得出函数值的大小关系.
【解析】∵ a2-a+1=+≥,函数f(x)在(0,+∞)上单调递减,
∴ ≥f(a2-a+1).故选B.
【答案】B
◆利用函数的单调性比较大小的方法
若已知函数y=f(x)在区间[a,b]上是增函数,x1,x2∈[a,b],则
当x1当x1>x2时,有f(x1)>f(x2).
减函数也有类似的性质.
利用此性质我们可以根据函数的单调性及自变量的大小比较函数值的大小.
D
解:由题意知,f(x)图象的对称轴为直线x=2,
且f(x)在(2,+∞)上单调递增.
又∵ f(1)=f(3),且3<4,∴ f(3)【答案】
◆分段函数单调性的判断方法
分段函数f(x)在R上单调递增(减),不仅每一段是单调递增(减)的,且两段的分界点处的函数值也要满足相应的大小关系,即保证在分段函数的分界点处,函数的图象不下降(上升).
训练题
1.已知函数f(x)的定义域为[-2,2],且f(x)在区间[-2,2]上是增函数,
f(1-m)【解】因为f(x)在区间[-2,2]上单调递增,且f(1-m)2.[2019·安徽蚌埠铁路中学高一检测]已知f(x)是定义在(0,+∞)上的增函数,且=f(x)-f(y).
(1)求f(1)的值; (2)若f(6)=1,解不等式f(x+3)-<2.
◆利用函数的单调性解函数值不等式的方法
1.利用函数在某个区间内的单调性,去掉对应关系“f ”,转化为自变量的不等式,此时一定要注意自变量的限制条件.
2.脱去“f ”的具体方法:
①若y=f(x)在[a,b]上单调递增,则f(g(x))?
②若y=f(x)在[a,b]上单调递减,则f(g(x))【答案】D
A
(2,5)
D
小结
两个知识点:
1.函数在区间上单调递增(递减);2.函数的增减性;
三种题型:
1.利用图象确定函数的单调区间;
2.证明函数的单调性;
3.函数单调性的应用.
知易行难,重在行动
千里之行,始于足下
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
数学-RJ·A-必修第一册
3.2.1 单调性与最大(小)值
第1课时
第三章 函数的概念与性质
重点:理解函数单调性的概念;判断函数的单调性.
难点:判断函数的单调性.
1.了解函数的单调区间、单调性等概念.
2.会划分函数的单调区间,判断单调性.
3.会用定义证明函数的单调性.
学习目标
知识梳理
一、函数在区间上单调递增(递减)
总结归纳
1.函数f(x)在区间D上是增函数,x1,x2∈D,且x1≠x2
(x1-x2)[f(x1)-f(x2)]>0
2.函数f(x)在区间D上是减函数,x1,x2∈D,且x1≠x2
(x1-x2)[f(x1)-f(x2)]<0
特别提醒
函数在区间上单调递增(递减)的定义是用数学符号来刻画函数的图象特征,它反映了函数图象的变化趋势(当自变量增大时,函数值是增大还是减小,图象是上升还是下降);函数y=f(x)在区间D上是单调递增(递减),等价于对于D中任意的两个自变量x1,x2,且x1
A.函数f(x)在区间[-1,2]上是增函数 B.函数f(x)在区间[-1,2]上是减函数
C.函数f(x)在区间[-1,4]上是减函数 D.函数f(x)在区间[2,4]上是增函数
答案:A
【做一做1-2】 已知函数y=f(x)在区间(a,b)内是单调递减,x1,x2∈(a,b),且x1
C.f(x1)=f(x2) D.以上都有可能
答案:B
二、函数的增减性
1.定义:如果函数y=f(x)在区间D上单调递增或单调递减,那么就说函数y=f(x)在这一区间具有(严格的)单调性,区间D叫做y=f(x)的单调区间.
2.图象特征:函数y=f(x)在区间D上具有单调性,则函数y=f(x)在区间D上的图象是上升的或下降的.
总结归纳
基本初等函数的单调区间如下表所示:
【做一做2】已知[0,3]是函数f(x)定义域内的一个区间,若f(1)
C.不单调递增就是单调递减 D.增减性不能确定
解析:虽然1,2∈[0,3],1<2,且f(1)
常考题型
一、用定义法判断和证明函数的单调性
◆用定义法证明函数的单调性的一般步骤
(1)取值,设x1,x2是给定区间内的任意两个值,且x1
(3)判号,确定f(x1)-f(x2)(或f(x2)- f(x1))的符号,当符号不确定时,要进行分类讨论.
(4)定论,根据定义得出结论.
◆用定义法证明函数的单调性常用的变形技巧
1.因式分解:当原函数是多项式函数时,通常作差后进行因式分解.
2.通分:当原函数是分式函数时,作差后往往先进行通分,然后对分子进行因式分解.
3.配方:当原函数是二次函数时,作差后可以考虑配方.
4.分子有理化:当原函数是根式函数时,作差后往往考虑分子有理化.
二、函数单调性的判断及单调区间的求解
◆含参函数单调性的两种类型及解法
1.作差变形后式子的符号与参数值无关,直接用定义判断.
2.作差变形后式子的符号与参数值有关,此时应对参数分类讨论.
C
2.图象法
例3 函数f(x)=|x-2|x的单调减区间是 ( )
A.[1,2] B.[-1,0]
C.[0,2] D.[2,+∞)
【答案】A
训练题
1.[2019·湖南衡阳市一中高一月考]函数y=|x2-3x-4|的单调
增区间是 .
,[4,+∞)
2.已知函数f(x)=-x2+2|x|+3.
(1)用分段函数的形式表示f(x); (2)画出f(x)的图象;
(3)根据图象写出f(x)的单调区间.
解:(1)当x≥0时,f(x)=-x2+2x+3=-(x-1)2+4;
当x<0时,f(x)=-x2-2x+3=-(x+1)2+4,
即f(x)
(2)函数f(x)的图象如图所示.
(3)函数f(x)的图象在区间(-∞,-1]和[0,1]上是上升的,
在区间(-1,0)和(1,+∞)内是下降的,
所以f(x)的单调递增区间是(-∞,-1],[0,1],单调递减区间是[-1,0],[1,+∞).
◆图象法
适用于已知函数图象或函数图象可以作出的函数.
图象法就是先画出函数的图象,然后利用图象直观判断函数的单调性.从左到右图象逐渐上升就是单调递增,逐渐下降就是单调递减.
f(x) g(x) f(x)+ g(x) f(x)-
g(x)
增 增 增 不确定
增 减 不确定 增
减 减 减 不确定
减 增 不确定 减
训练题
1.[2019·安徽芜湖高一月考]函数f(x)=1- ( )
A.在(-1,+∞)上单调递增 B.在(1,+∞)上单调递增
C.在(-1,+∞)上单调递减 D.在(1,+∞)上单调递减
B
2.[2020·上海市育才中学高一月考]已知函数f(x)=x2,x∈[1,+∞),判断该函数的单调性,并证明.
【解题提示】设t=x2+3x-4,由t≥0,可得x≤-4或x≥1,则运用复合函数的单调性(同增异减),以及二次函数和幂函数的单调性,即可得到所求的单调区间.
【答案】[1,+∞)
◆判断复合函数的单调性的方法
1.对于复合函数y=f(g(x)),如果u=g(x)在(a,b)上是单调函数,
并且y=f(u)在(g(a),g(b))或者(g(b),g(a))上也是单调
函数,则y=f(g(x))在(a,b)上的单调性如下表所示:
u=g(x) y=f(u) y=f(g(x))
增 增 增
增 减 减
减 增 减
减 减 增
简记为“同增异减”.
2.若一个函数是由多个简单函数复合而成的,则此复合函数的单调性由简单函数中减函数的个数决定.若减函数有偶数个,则这个复合函数为增函数;若减函数有奇数个,则这个复合函数为减函数.
(-∞,0) 和[1,+∞)
(0,1]
5.抽象函数的单调性
例6[2020·安徽庐江二中高一检测]已知函数f(x)对任意的a,b∈,都有f(a+b)=f(a)+f(b)-1,并且当x>0时,f(x)>1.
(1)求证:f(x)是R上的增函数;
(2)若f(4)=5,解不等式f(3m2-m-2)<3.
(1)【证明】任取x1,x2∈R,且x1
∴ f(x2)-f(x1)=f((x2-x1)+x1)-f(x1)
=f(x2-x1)+f(x1)-1-f(x1)=f(x2-x1)-1>0,∴ f(x1)
◆判断抽象函数的单调性的方法
1.抽象函数的单调性一般用定义法来判断,其一般步骤为
(1)在所证区间上设出x1,x2(x1
(f(x1)
(3)由定义得出结论.
训练题 [2019·河南南阳高一检测]已知定义在上的函数对任意x,y∈(0,+∞),恒有f(xy)=f(x)+f(y),且当0
三、函数单调性的应用
1.利用函数的单调性比较大小
例7 [2020·陕西西电附中高一月考]若函数f(x)的定义域为R,且在(0,+∞)上单调递减,则下列不等式成立的是 ( )
A.>f(a2-a+1) B.≥f(a2-a+1) C.
【解析】∵ a2-a+1=+≥,函数f(x)在(0,+∞)上单调递减,
∴ ≥f(a2-a+1).故选B.
【答案】B
◆利用函数的单调性比较大小的方法
若已知函数y=f(x)在区间[a,b]上是增函数,x1,x2∈[a,b],则
当x1
减函数也有类似的性质.
利用此性质我们可以根据函数的单调性及自变量的大小比较函数值的大小.
D
解:由题意知,f(x)图象的对称轴为直线x=2,
且f(x)在(2,+∞)上单调递增.
又∵ f(1)=f(3),且3<4,∴ f(3)
◆分段函数单调性的判断方法
分段函数f(x)在R上单调递增(减),不仅每一段是单调递增(减)的,且两段的分界点处的函数值也要满足相应的大小关系,即保证在分段函数的分界点处,函数的图象不下降(上升).
训练题
1.已知函数f(x)的定义域为[-2,2],且f(x)在区间[-2,2]上是增函数,
f(1-m)
(1)求f(1)的值; (2)若f(6)=1,解不等式f(x+3)-<2.
◆利用函数的单调性解函数值不等式的方法
1.利用函数在某个区间内的单调性,去掉对应关系“f ”,转化为自变量的不等式,此时一定要注意自变量的限制条件.
2.脱去“f ”的具体方法:
①若y=f(x)在[a,b]上单调递增,则f(g(x))
②若y=f(x)在[a,b]上单调递减,则f(g(x))
A
(2,5)
D
小结
两个知识点:
1.函数在区间上单调递增(递减);2.函数的增减性;
三种题型:
1.利用图象确定函数的单调区间;
2.证明函数的单调性;
3.函数单调性的应用.
知易行难,重在行动
千里之行,始于足下
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
