【课件】3.3 幂函数 高中数学-RJ·A-必修第一册 (共37张PPT)
文档属性
| 名称 | 【课件】3.3 幂函数 高中数学-RJ·A-必修第一册 (共37张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-19 18:28:14 | ||
图片预览









文档简介
(共37张PPT)
数学-RJ·A-必修第一册
3.3 幂函数
第三章 函数的概念与性质
学习目标
1.了解幂函数的概念.
2.结合函数y=x,y=x2,y=x3,y=x-1,的图象,了解它们的变化情况.
重点:从五个具体幂函数中认识幂函数的一些性质.
难点:画幂函数的图象,并由图象概括其性质.
知识梳理
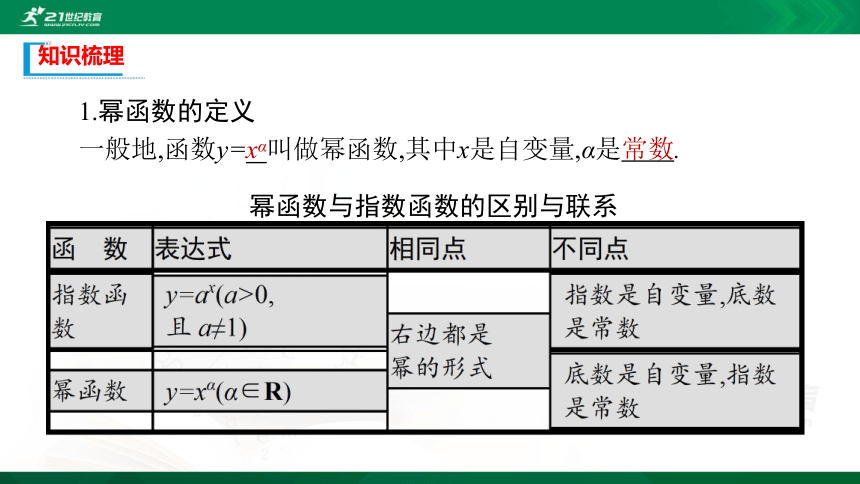
1.幂函数的定义
一般地,函数y=xα叫做幂函数,其中x是自变量,α是常数.
幂函数与指数函数的区别与联系
A.1 B.2
C.3 D.4
解析:②⑦为指数函数,③中系数不是1,④中解析式为多项式,⑤中底数不是自变量本身,所以只有①⑥是幂函数,故选B.
答案:B
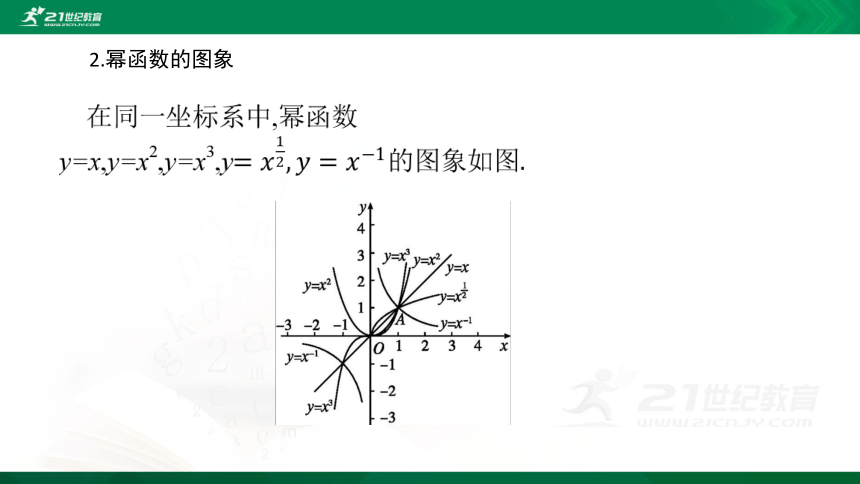
2.幂函数的图象
归纳总结
幂函数在第一象限内的指数变化规律:在第一象限内直线x=1的右侧,图象从上到下,相应的指数由大变小,即指数大的在上边.
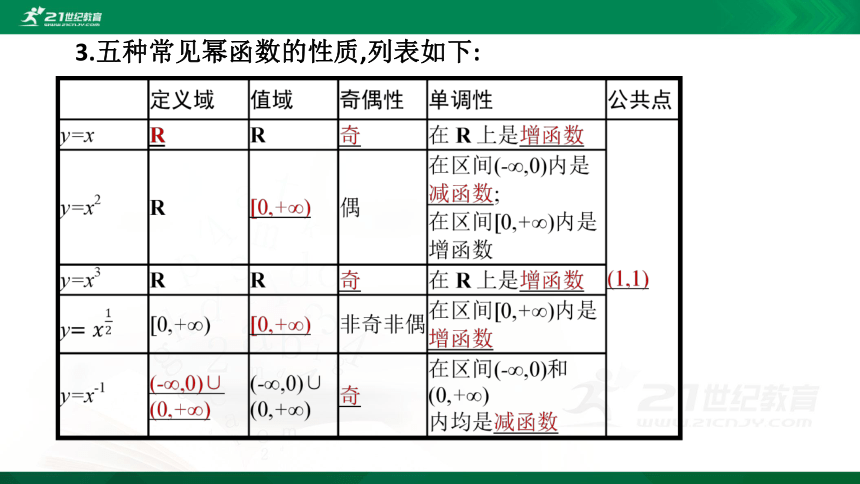
3.五种常见幂函数的性质,列表如下:
幂函数有如下性质:
(1)所有的幂函数在区间(0,+∞)内都有意义,图象都通过点(1,1),并且幂函数的图象都不过第四象限.
(2)当α>0时,幂函数的图象都通过点(0,0),(1,1),并且在区间[0,+∞)内都是增函数.当α<0时,幂函数的图象都通过点(1,1),在区间(0,+∞)内都是减函数,在第一象限内,函数图象向上与y轴无限接近,向右与x轴无限接近.
知识拓展
【做一做2】 下列结论正确的是( )
A.幂函数的图象都通过点(0,0),(1,1)
B.幂函数的图象可以出现在第四象限
D.当幂指数α=-1时,幂函数y=xα在定义域上是减函数
解析:当幂指数α=-1时,幂函数y=x-1的图象不通过原点,故选项A不正确;
因为所有的幂函数在区间(0,+∞)内都有定义,且y=xα(α∈R),y>0,所以幂函数的图象不可能出现在第四象限,故选项B不正确;
当α=-1时,y=x-1在区间(-∞,0)和(0,+∞)内是减函数,但在它的定义域上不是减函数,
故选项D不正确.故选C.
答案:C
常考题型
一、幂函数的概念
1. 幂函数的判断
例1 幂函数f(x)=(m2-3m+3)xm的图象关于y轴对称,则实数m= .
【解析】∵ f(x)=(m2-3m+3)xm是幂函数,∴ m2-3m+3=1,
∴m=1或m=2.
当m=1时,函数f(x)=x的图象不关于y轴对称,舍去;
当m=2时,函数f(x)=x2的图象关于y轴对称,符合题意.
综上可知,m=2.
【答案】2
◆幂函数的判断的一般方法
幂函数y=xα的三个特征:
①系数为1;②底数只能是自变量x;③幂指数是常数.
只有满足这三个特征,才是幂函数.
训练题
1.[2020·湖南衡阳县四中高一月考]下列函数既是偶函数又是幂函数的是 ( )
A.y=x B.y= C.y= D.y=|x|
2.[2019·山西涑北中学高一月考]已知函数f (x)=(m2+m-1)xm+3是幂函数,且该函数是偶函数,则m的值是 .
C
1
2. 确定幂函数的解析式、定义域和值域
例2 已知幂函数f(x)=xa的图象经过点(2,),则a= .
不等式f(x)>3的解集为 .
【解析】由题意,将点(2,)的坐标代入f(x)=xa,得2a==,
∴ a=.不等式f(x)>3,即>3,∴ x>9.
【答案】 (9,+∞)
◆待定系数法确定幂函数的解析式
1.设出幂函数的解析式y=xα;2.将图象上的点的坐标代入解析式得关于α的方程;
3.求出参数α; 4.代回得幂函数的解析式.
◆幂函数的定义域和值域的求法
1.当α=0时,的定义域为,值域为.
2.当α为正整数时,的定义域为,α为正偶数时,值域为[0,+∞),α为正奇数时,值域为.
3.当为负整数时,的定义域为为负偶数时,值域为为负奇数时,值域为.
B
B
二、幂函数的图象及其应用
1. 图象的画法与识别
例3 [2020·重庆八中高一检测]幂函数f(x)=xα(α∈)的图象经过点
(8,4),则幂函数f(x)的大致图象是 ( )
A B C D
【解析】∵ f(x)=xα(α∈)的图象经过点(8,4),
∴ f(8)=4,即8α=4,α=,
∴ f(x)=,f(x)为偶函数,故选C.
【答案】C
◆幂函数图象的识别和作法
1.当α>0时,
(1)图象都过点(0,0),(1,1);
(2)在第一象限内,函数值随x的增大而增大;
(3)在第一象限内,α>1时,图象是向下凸的,0<α<1时,图象是向上凸的;
(4)在第一象限内,过(1,1)点后,图象向右上方无限伸展.
2.当α<0时,
(1)图象都过点(1,1);
(2)在第一象限内,函数值随x的增大而减小,图象是向下凸的;
(3)在第一象限内,图象向左与y轴无限接近,向右与x轴无限接近;
(4)在第一象限内,过(1,1)点后,|α|越大,图象下落的速度越快.
训练题
1.[2019·湖南衡阳高一期末]下列命题正确的是 ( )
A.幂函数的图象都经过(0,0),(1,1)两点
B.当n=0时,函数y=xn的图象是一条直线
C.如果两个幂函数的图象至少有三个公共点,那么这两个函数一定相同
D.如果幂函数为偶函数,则图象一定经过点(-1,1)
D
2.[2019·黑龙江哈尔滨高一期末]图中给出四个幂函数的图象,则图象与函数大致对应的是 ( )
① ② ③ ④
B
2. 图象的应用
例4 [2020·上海曹杨中学高一期末]设y=f(x)和y=g(x)是两个不同的幂函数,集合M={(x,y)|f(x)=g(x)},则集合M中元素的个数为 ( )
A.1或2或0 B.1或2或3
C.1或2或3或4 D.0或1或2或3
【解析】任意幂函数的图象必过点(1,1),
故(1,1)∈M,故排除A,D.
任意两个幂函数的图象不可能有4个交点,故排除C.
故选B.
【答案】B
训练题
1.已知幂函数f(x)=(m∈)的图象关于y轴对称,
且在区间(0,+∞)上单调递减,则m的值为 .
2.[2019·福建三明高一期末]函数f(x)=xa+b,不论a为
何值,f(x)的图象均过点(m,m),则实数b的值为( )
A.0 B.1 C.2 D.3
2
A
三、幂函数的性质及其应用
1.幂函数的性质
【解析】 设f(x)=xa,因为函数f(x)的图象经过点,所以2a==2-3,解得a=-3,根据幂函数f(x)=x-3的图象如图所示,可知①不正确,②正确,③说法有误,
【答案】②④
C
④
2.比较幂的大小
例6 [2020·山东淄博一中高一检测]已知a=20.4,b=30.2 ,c=50.2 ,则( )
A.a【解析】由已知可得a=20.4=(22)0.2=40.2.因为幂函数y=x0.2在(0,+∞)
上单调递增,且3<4<5,所以30.2<40.2<50.2,即b【答案】B
◆比较幂的大小的方法
比较两个幂值的大小,关键是构造适当的函数.若指数相同而底数不同,则考虑幂函数;若指数不同而底数相同,则考虑借助函数的图象来比较.
训练题
1.比较下列各组数中两个数的大小:
解:(1)∵幂函数y[0,+∞)内是增函数,
(2)∵幂函数y=x-1在区间(-∞,0)内是减函数,
(3)∵函数y1R上为减函数,
又函数y2[0,+∞)内是增函数,
2.已知(0.71.3)m<(1.30.7)m,求m的取值范围.
解:根据幂函数y=x1.3的图象(图略),可知当01时,y>1,∴ 1.30.7>1.于是有0.71.3<1.30.7.
对于幂函数y=xm,由(0.71.3)m<(1.30.7)m知,当x>0时,随着自变量x的增大,函数值y也增大,
∴ m的取值范围是(0,+∞).
◆已知单调性、奇偶性求参数的思路
关键是利用幂函数的单调性和奇偶性进行合理转化,列出含参数的方程(组)或不等式(组)求解.
0
解:因为f(x)在(0,+∞)上单调递减,所以m2-2m-3<0,
所以-1当m=0时,f(x)=x-3,为奇函数,舍去;
当m=1时,f(x)=x-4,为偶函数,符合题意;
当m=2时,f(x)=x-3,为奇函数,舍去.
故f(x)=x-4.
【答案】
◆利用幂函数的单调性解不等式的一般步骤
利用幂函数解不等式,实质是已知两个函数值的大小,判断自变量的大小,常与幂函数的单调性、奇偶性等综合命题,求解步骤如下:
(1)确定可以利用的幂函数;
(2)借助相应幂函数的单调性,将不等式的大小关系转化为自变量的大小关系;
(3)解不等式(组)求参数的取值范围,注意分类讨论思想的应用.
训练题
1.[2019·湖北荆州高三检测]若对任意的x∈[a,a+2],均有
(3x+a)3≤8x3,则实数a的取值范围是 ( )
A.(-∞,-2] B.(-∞,-1] C.(-∞,0] D.[0,+∞)
2.[2020·四川高一检测]已知幂函数f(x)=(m2-m-1)x-2m-1在(0,+∞)上单调递增.
(1)求实数m的值.
(2)若(k+1)m<(3-2k)m,求实数k的取值范围.
B
解:(1)因为f(x)是幂函数,所以m2-m-1=1,解得m=-1或m=2.
又因为f(x)在(0,+∞)上单调递增,
所以-2m-1>0,即m<,所以m=-1.
小结
二个知识点:
1.幂函数的定义;2.幂函数的图象;3.五种常见幂函数的性质.
四种题型:
1.幂函数的概念问题;
2.幂函数的图象问题;
3.比较幂的大小.
知易行难,重在行动
千里之行,始于足下
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
数学-RJ·A-必修第一册
3.3 幂函数
第三章 函数的概念与性质
学习目标
1.了解幂函数的概念.
2.结合函数y=x,y=x2,y=x3,y=x-1,的图象,了解它们的变化情况.
重点:从五个具体幂函数中认识幂函数的一些性质.
难点:画幂函数的图象,并由图象概括其性质.
知识梳理
1.幂函数的定义
一般地,函数y=xα叫做幂函数,其中x是自变量,α是常数.
幂函数与指数函数的区别与联系
A.1 B.2
C.3 D.4
解析:②⑦为指数函数,③中系数不是1,④中解析式为多项式,⑤中底数不是自变量本身,所以只有①⑥是幂函数,故选B.
答案:B
2.幂函数的图象
归纳总结
幂函数在第一象限内的指数变化规律:在第一象限内直线x=1的右侧,图象从上到下,相应的指数由大变小,即指数大的在上边.
3.五种常见幂函数的性质,列表如下:
幂函数有如下性质:
(1)所有的幂函数在区间(0,+∞)内都有意义,图象都通过点(1,1),并且幂函数的图象都不过第四象限.
(2)当α>0时,幂函数的图象都通过点(0,0),(1,1),并且在区间[0,+∞)内都是增函数.当α<0时,幂函数的图象都通过点(1,1),在区间(0,+∞)内都是减函数,在第一象限内,函数图象向上与y轴无限接近,向右与x轴无限接近.
知识拓展
【做一做2】 下列结论正确的是( )
A.幂函数的图象都通过点(0,0),(1,1)
B.幂函数的图象可以出现在第四象限
D.当幂指数α=-1时,幂函数y=xα在定义域上是减函数
解析:当幂指数α=-1时,幂函数y=x-1的图象不通过原点,故选项A不正确;
因为所有的幂函数在区间(0,+∞)内都有定义,且y=xα(α∈R),y>0,所以幂函数的图象不可能出现在第四象限,故选项B不正确;
当α=-1时,y=x-1在区间(-∞,0)和(0,+∞)内是减函数,但在它的定义域上不是减函数,
故选项D不正确.故选C.
答案:C
常考题型
一、幂函数的概念
1. 幂函数的判断
例1 幂函数f(x)=(m2-3m+3)xm的图象关于y轴对称,则实数m= .
【解析】∵ f(x)=(m2-3m+3)xm是幂函数,∴ m2-3m+3=1,
∴m=1或m=2.
当m=1时,函数f(x)=x的图象不关于y轴对称,舍去;
当m=2时,函数f(x)=x2的图象关于y轴对称,符合题意.
综上可知,m=2.
【答案】2
◆幂函数的判断的一般方法
幂函数y=xα的三个特征:
①系数为1;②底数只能是自变量x;③幂指数是常数.
只有满足这三个特征,才是幂函数.
训练题
1.[2020·湖南衡阳县四中高一月考]下列函数既是偶函数又是幂函数的是 ( )
A.y=x B.y= C.y= D.y=|x|
2.[2019·山西涑北中学高一月考]已知函数f (x)=(m2+m-1)xm+3是幂函数,且该函数是偶函数,则m的值是 .
C
1
2. 确定幂函数的解析式、定义域和值域
例2 已知幂函数f(x)=xa的图象经过点(2,),则a= .
不等式f(x)>3的解集为 .
【解析】由题意,将点(2,)的坐标代入f(x)=xa,得2a==,
∴ a=.不等式f(x)>3,即>3,∴ x>9.
【答案】 (9,+∞)
◆待定系数法确定幂函数的解析式
1.设出幂函数的解析式y=xα;2.将图象上的点的坐标代入解析式得关于α的方程;
3.求出参数α; 4.代回得幂函数的解析式.
◆幂函数的定义域和值域的求法
1.当α=0时,的定义域为,值域为.
2.当α为正整数时,的定义域为,α为正偶数时,值域为[0,+∞),α为正奇数时,值域为.
3.当为负整数时,的定义域为为负偶数时,值域为为负奇数时,值域为.
B
B
二、幂函数的图象及其应用
1. 图象的画法与识别
例3 [2020·重庆八中高一检测]幂函数f(x)=xα(α∈)的图象经过点
(8,4),则幂函数f(x)的大致图象是 ( )
A B C D
【解析】∵ f(x)=xα(α∈)的图象经过点(8,4),
∴ f(8)=4,即8α=4,α=,
∴ f(x)=,f(x)为偶函数,故选C.
【答案】C
◆幂函数图象的识别和作法
1.当α>0时,
(1)图象都过点(0,0),(1,1);
(2)在第一象限内,函数值随x的增大而增大;
(3)在第一象限内,α>1时,图象是向下凸的,0<α<1时,图象是向上凸的;
(4)在第一象限内,过(1,1)点后,图象向右上方无限伸展.
2.当α<0时,
(1)图象都过点(1,1);
(2)在第一象限内,函数值随x的增大而减小,图象是向下凸的;
(3)在第一象限内,图象向左与y轴无限接近,向右与x轴无限接近;
(4)在第一象限内,过(1,1)点后,|α|越大,图象下落的速度越快.
训练题
1.[2019·湖南衡阳高一期末]下列命题正确的是 ( )
A.幂函数的图象都经过(0,0),(1,1)两点
B.当n=0时,函数y=xn的图象是一条直线
C.如果两个幂函数的图象至少有三个公共点,那么这两个函数一定相同
D.如果幂函数为偶函数,则图象一定经过点(-1,1)
D
2.[2019·黑龙江哈尔滨高一期末]图中给出四个幂函数的图象,则图象与函数大致对应的是 ( )
① ② ③ ④
B
2. 图象的应用
例4 [2020·上海曹杨中学高一期末]设y=f(x)和y=g(x)是两个不同的幂函数,集合M={(x,y)|f(x)=g(x)},则集合M中元素的个数为 ( )
A.1或2或0 B.1或2或3
C.1或2或3或4 D.0或1或2或3
【解析】任意幂函数的图象必过点(1,1),
故(1,1)∈M,故排除A,D.
任意两个幂函数的图象不可能有4个交点,故排除C.
故选B.
【答案】B
训练题
1.已知幂函数f(x)=(m∈)的图象关于y轴对称,
且在区间(0,+∞)上单调递减,则m的值为 .
2.[2019·福建三明高一期末]函数f(x)=xa+b,不论a为
何值,f(x)的图象均过点(m,m),则实数b的值为( )
A.0 B.1 C.2 D.3
2
A
三、幂函数的性质及其应用
1.幂函数的性质
【解析】 设f(x)=xa,因为函数f(x)的图象经过点,所以2a==2-3,解得a=-3,根据幂函数f(x)=x-3的图象如图所示,可知①不正确,②正确,③说法有误,
【答案】②④
C
④
2.比较幂的大小
例6 [2020·山东淄博一中高一检测]已知a=20.4,b=30.2 ,c=50.2 ,则( )
A.a
上单调递增,且3<4<5,所以30.2<40.2<50.2,即b
◆比较幂的大小的方法
比较两个幂值的大小,关键是构造适当的函数.若指数相同而底数不同,则考虑幂函数;若指数不同而底数相同,则考虑借助函数的图象来比较.
训练题
1.比较下列各组数中两个数的大小:
解:(1)∵幂函数y[0,+∞)内是增函数,
(2)∵幂函数y=x-1在区间(-∞,0)内是减函数,
(3)∵函数y1R上为减函数,
又函数y2[0,+∞)内是增函数,
2.已知(0.71.3)m<(1.30.7)m,求m的取值范围.
解:根据幂函数y=x1.3的图象(图略),可知当0
对于幂函数y=xm,由(0.71.3)m<(1.30.7)m知,当x>0时,随着自变量x的增大,函数值y也增大,
∴ m的取值范围是(0,+∞).
◆已知单调性、奇偶性求参数的思路
关键是利用幂函数的单调性和奇偶性进行合理转化,列出含参数的方程(组)或不等式(组)求解.
0
解:因为f(x)在(0,+∞)上单调递减,所以m2-2m-3<0,
所以-1
当m=1时,f(x)=x-4,为偶函数,符合题意;
当m=2时,f(x)=x-3,为奇函数,舍去.
故f(x)=x-4.
【答案】
◆利用幂函数的单调性解不等式的一般步骤
利用幂函数解不等式,实质是已知两个函数值的大小,判断自变量的大小,常与幂函数的单调性、奇偶性等综合命题,求解步骤如下:
(1)确定可以利用的幂函数;
(2)借助相应幂函数的单调性,将不等式的大小关系转化为自变量的大小关系;
(3)解不等式(组)求参数的取值范围,注意分类讨论思想的应用.
训练题
1.[2019·湖北荆州高三检测]若对任意的x∈[a,a+2],均有
(3x+a)3≤8x3,则实数a的取值范围是 ( )
A.(-∞,-2] B.(-∞,-1] C.(-∞,0] D.[0,+∞)
2.[2020·四川高一检测]已知幂函数f(x)=(m2-m-1)x-2m-1在(0,+∞)上单调递增.
(1)求实数m的值.
(2)若(k+1)m<(3-2k)m,求实数k的取值范围.
B
解:(1)因为f(x)是幂函数,所以m2-m-1=1,解得m=-1或m=2.
又因为f(x)在(0,+∞)上单调递增,
所以-2m-1>0,即m<,所以m=-1.
小结
二个知识点:
1.幂函数的定义;2.幂函数的图象;3.五种常见幂函数的性质.
四种题型:
1.幂函数的概念问题;
2.幂函数的图象问题;
3.比较幂的大小.
知易行难,重在行动
千里之行,始于足下
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
