【课件】5.1任意角和弧度制 5.1.2弧度制 高中数学-RJA-必修第一册 (共29张PPT)
文档属性
| 名称 | 【课件】5.1任意角和弧度制 5.1.2弧度制 高中数学-RJA-必修第一册 (共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-19 00:00:00 | ||
图片预览








文档简介
(共29张PPT)
数学-RJ·A-必修第一册
5.1 任意角和弧度制
5.1.2 弧度制
第五章 三角函数
学习目标
1.了解弧度制,体会引入弧度制的必要性.
2.理解1弧度的角及弧度的定义.
3.掌握角度与弧度的换算公式,能进行角度与弧度的换算,并熟记几个特殊角的弧度数.
4.掌握弧度制中扇形的弧长公式和面积公式.
重点:了解弧度制,并能进行弧度与角度的换算.
难点:弧度的概念.
知识梳理
用度作为单位来度量角的单位制叫做 .
把长度等于半径长的圆弧所对的圆心角叫做 的角,用符号rad表示,读作弧度.
我们把半径为1的圆叫做单位圆.
如图,单位圆O中,的长等于1,
∠AOB就是1弧度的角.
一、角度制、弧度制的相关概念
角度制
1弧度
一般地,正角的弧度数是一个 ,负角的弧度数是一个 ,
零角的弧度数是 .
正数
二、角度与弧度的换算
负数
0
弧度与角度换算公式:
如果半径为r的圆的圆心角α所对弧的长为l,那么,角α的弧度数的绝对
值是|α|= .
例1
一 弧度制的概念的理解
常考题型
在大小不同的圆中,1 rad的圆心角所对的 ( )
A.弦长相等 B.弧长相等
C.弦长等于所在圆的半径 D.弧长等于所在圆的半径
【解析】 由弧度制的定义,1弧度的角就是所对弧长与半径之比等于1的角,所以1 rad的圆心角所对的弧长等于所在圆的半径.
【答案】 D
正确理解弧度制
1.圆心角所对的弧长与半径的比值,与圆半径的大小无关,只与角的大小有关,因而可用这个比值来度量圆心角,即|α|=(l表示弧长).
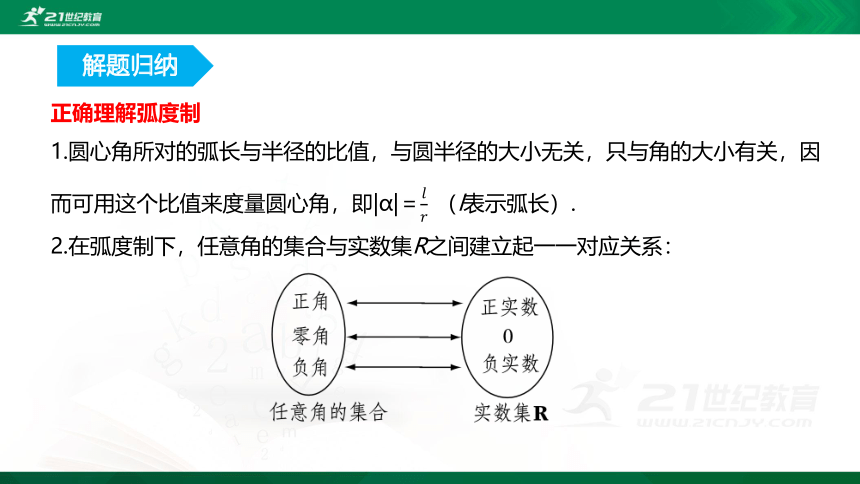
2.在弧度制下,任意角的集合与实数集R之间建立起一一对应关系:
解题归纳
1.[2020·上海高一检测]下列选项中,错误的是( )
A.“度”与“弧度”是度量角的两种不同的度量单位
B.一度的角是周角的,一弧度的角是周角的
C.180度一定等于π弧度
D.无论用角度制还是弧度制度量角,它们与圆的半径长短有关
训练题
2.[2020·上海市行知中学高一检测]一场数学科目考试需要两个小时,则时针走了 弧度.
例2
二 角度与弧度的互化
下列互化结果错误的是( )
A.60°化成弧度是rad B.π rad化成度是-600°
C.-150°化成弧度是rad D.rad化成度是12°
【解】 对于A,60°=60×rad=rad;
对于B,π rad= =-600°;
对于C,-150°=-150×rad=rad;
对于D,rad= =12°.
【答案】 C
角度与弧度的换算公式
角度化弧度 弧度化角度
360°=2π rad 2π rad=360°
180°=π rad π rad=180°
1°=rad 1 rad= ≈57.30°
角度数×=弧度数 弧度数× =角度数
解题归纳
训练题
[2019·黑龙江牡丹江三中高一检测]下列各式中,不正确的是( )
A.45°ad B.60°=rad
C.-210°=rad D.725°=rad
1.
将下列角度与弧度进行互化:rad= ;112°30′= .
2.
-105°
D
rad
三 弧度制下终边相同的角的表示及其应用
例3
将-1 125°表示成2kπ+α(k∈Z,0≤α<2π)的形式,并在[-4π,0)上找出与角-1 125°终边相同的角.
【解题提示】 先把-1 125°化成k·360°+α(k∈Z)的形式,再用弧度制表示.
【解】 -1 125°=-4×360°+315°,而315°=315×rad=rad,
故-1 125°=-4×2π+rad.
∴ 与角-1 125°终边相同的角为β=2kπ+(k∈Z).
由-4π≤2kπ+<0,得≤k<.又k∈Z,∴ k=-1或-2.
当k=-1时,β=;当k=-2时,β=.
故在[-4π,0)上与角-1 125°终边相同的角为, .
弧度制下终边相同角的表示
1.与角α终边相同的角,连同角α在内,构成集合S={β|β=2kπ+α,k∈Z}.
2. 用弧度制表示终边相同的角α+2kπ(k∈Z)时,注意2kπ是π的偶数倍.
3.在进行“弧度”与“角度”换算时,若无特别要求,不可进行近似计算,也不必将π化为小数.
4.角度制和弧度制不得混用,如α=2kπ+60°(k∈Z),β=k·360°+(k∈Z)都是不正确的写法.
解题归纳
训练题
1.
若角θ的终边与角的终边相同,则在[0,2π)内终边与角的终
边相同的角为 .
2.
将下列各角化成2kπ+α(0≤α<2π,k∈Z)的形式,并指出是第几象限角:(1)-1 500°;(2);(3)-4.
【解】(1)∵-1 500°=-1 800°+300°=-5×360°+300°
= rad,∴ -1 500°角与角的终边相同,是第四象限角.
(2)∵=2π+,∴ 角与角的终边相同,是第四象限角.
(3)∵-4=-2π+(2π-4),
∴-4角与2π-4角的终边相同,是第二象限角.
[2020·南京校级联考]若角α的终边与角的终边关于直线y=x对称,且
α∈(-4π,4π),则α= .
3.
4.
若角α的终边在如图所示的阴影部分(包括边界),
则角α的取值范围是( )
A. B.
C. D.
用弧度制表示区域角应关注的三点
1.用弧度表示区域角,必要时需进行角度与弧度的换算,注意单位要统一.
2.在表示角的集合时,可以先写出一周范围内的角(如-π~π,0~2π),再加上2kπ,k∈Z.
3.终边在同一条直线上的角的集合可以表示为{x|x=α+kπ,k∈Z};终边在相互垂直的两条直线上的角的集合可以表示为.
解题归纳
四 与弧长、扇形面积有关的问题
例4
(1)[2019·广东珠海模拟]已知扇形的周长是4 cm,则扇形面积最大时,扇形的圆心角的弧度数是( )
A.2 B.1 C. D.3
(2)[2019·广西贺州高二检测]已知扇形的圆心角为,面积为,则扇形的弧长等于 .
【解析】 (1)设扇形的半径为R cm,则弧长l=(4-2R)cm,
∴ 扇形面积S=lR=R(2-R)=-R2+2R=-(R-1)2+1.
当R=1时,S最大,此时l=2,扇形圆心角为2弧度.
(2)设扇形的半径为r,弧长为l,则解得
【答案】 (1)A (2)
【方法点拨】
1.已知圆心角的度量单位为角度制时,可直接使用角度制下扇形的弧长和面积公式:(1)弧长公式:l=;(2)面积公式:=.
2.已知圆心角的度量单位为弧度制时,可使用弧度制下扇形的弧长和面积公式:
(1)弧长公式:l=αr;
(2)面积公式:=lr=|α|r2.
解题归纳
训练题
[2020·黑龙江大庆市第十中学高一期末]已知扇形的半径为2,圆心角为2弧度,则该扇形的面积为 .
1.
2.
[2020·安徽省太和县第一中学高一期末]已知一扇形的面积是8 cm2,周长是12 cm,则该扇形的圆心角α(0<α<π)的弧度数是 .
使用弧度制下扇形的弧长和面积公式应注意
①在扇形的弧长公式与面积公式中,各含有三个量,因此可知二求一;
②使用公式时,注意角α的单位只能是弧度,而不是角度;
③弧度制下扇形面积公式S=lr,类似于三角形面识公式S=ah(其中h是三角形中长度为a的边上的高),可类比记忆.
解题归纳
小结
1.角度与弧度的换算
2.弧长公式、扇形面积公式
角度制 弧度制
弧长 公式 = =|α|r
扇形 面积 公式 = =
知易行难,重在行动
千里之行,始于足下
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
数学-RJ·A-必修第一册
5.1 任意角和弧度制
5.1.2 弧度制
第五章 三角函数
学习目标
1.了解弧度制,体会引入弧度制的必要性.
2.理解1弧度的角及弧度的定义.
3.掌握角度与弧度的换算公式,能进行角度与弧度的换算,并熟记几个特殊角的弧度数.
4.掌握弧度制中扇形的弧长公式和面积公式.
重点:了解弧度制,并能进行弧度与角度的换算.
难点:弧度的概念.
知识梳理
用度作为单位来度量角的单位制叫做 .
把长度等于半径长的圆弧所对的圆心角叫做 的角,用符号rad表示,读作弧度.
我们把半径为1的圆叫做单位圆.
如图,单位圆O中,的长等于1,
∠AOB就是1弧度的角.
一、角度制、弧度制的相关概念
角度制
1弧度
一般地,正角的弧度数是一个 ,负角的弧度数是一个 ,
零角的弧度数是 .
正数
二、角度与弧度的换算
负数
0
弧度与角度换算公式:
如果半径为r的圆的圆心角α所对弧的长为l,那么,角α的弧度数的绝对
值是|α|= .
例1
一 弧度制的概念的理解
常考题型
在大小不同的圆中,1 rad的圆心角所对的 ( )
A.弦长相等 B.弧长相等
C.弦长等于所在圆的半径 D.弧长等于所在圆的半径
【解析】 由弧度制的定义,1弧度的角就是所对弧长与半径之比等于1的角,所以1 rad的圆心角所对的弧长等于所在圆的半径.
【答案】 D
正确理解弧度制
1.圆心角所对的弧长与半径的比值,与圆半径的大小无关,只与角的大小有关,因而可用这个比值来度量圆心角,即|α|=(l表示弧长).
2.在弧度制下,任意角的集合与实数集R之间建立起一一对应关系:
解题归纳
1.[2020·上海高一检测]下列选项中,错误的是( )
A.“度”与“弧度”是度量角的两种不同的度量单位
B.一度的角是周角的,一弧度的角是周角的
C.180度一定等于π弧度
D.无论用角度制还是弧度制度量角,它们与圆的半径长短有关
训练题
2.[2020·上海市行知中学高一检测]一场数学科目考试需要两个小时,则时针走了 弧度.
例2
二 角度与弧度的互化
下列互化结果错误的是( )
A.60°化成弧度是rad B.π rad化成度是-600°
C.-150°化成弧度是rad D.rad化成度是12°
【解】 对于A,60°=60×rad=rad;
对于B,π rad= =-600°;
对于C,-150°=-150×rad=rad;
对于D,rad= =12°.
【答案】 C
角度与弧度的换算公式
角度化弧度 弧度化角度
360°=2π rad 2π rad=360°
180°=π rad π rad=180°
1°=rad 1 rad= ≈57.30°
角度数×=弧度数 弧度数× =角度数
解题归纳
训练题
[2019·黑龙江牡丹江三中高一检测]下列各式中,不正确的是( )
A.45°ad B.60°=rad
C.-210°=rad D.725°=rad
1.
将下列角度与弧度进行互化:rad= ;112°30′= .
2.
-105°
D
rad
三 弧度制下终边相同的角的表示及其应用
例3
将-1 125°表示成2kπ+α(k∈Z,0≤α<2π)的形式,并在[-4π,0)上找出与角-1 125°终边相同的角.
【解题提示】 先把-1 125°化成k·360°+α(k∈Z)的形式,再用弧度制表示.
【解】 -1 125°=-4×360°+315°,而315°=315×rad=rad,
故-1 125°=-4×2π+rad.
∴ 与角-1 125°终边相同的角为β=2kπ+(k∈Z).
由-4π≤2kπ+<0,得≤k<.又k∈Z,∴ k=-1或-2.
当k=-1时,β=;当k=-2时,β=.
故在[-4π,0)上与角-1 125°终边相同的角为, .
弧度制下终边相同角的表示
1.与角α终边相同的角,连同角α在内,构成集合S={β|β=2kπ+α,k∈Z}.
2. 用弧度制表示终边相同的角α+2kπ(k∈Z)时,注意2kπ是π的偶数倍.
3.在进行“弧度”与“角度”换算时,若无特别要求,不可进行近似计算,也不必将π化为小数.
4.角度制和弧度制不得混用,如α=2kπ+60°(k∈Z),β=k·360°+(k∈Z)都是不正确的写法.
解题归纳
训练题
1.
若角θ的终边与角的终边相同,则在[0,2π)内终边与角的终
边相同的角为 .
2.
将下列各角化成2kπ+α(0≤α<2π,k∈Z)的形式,并指出是第几象限角:(1)-1 500°;(2);(3)-4.
【解】(1)∵-1 500°=-1 800°+300°=-5×360°+300°
= rad,∴ -1 500°角与角的终边相同,是第四象限角.
(2)∵=2π+,∴ 角与角的终边相同,是第四象限角.
(3)∵-4=-2π+(2π-4),
∴-4角与2π-4角的终边相同,是第二象限角.
[2020·南京校级联考]若角α的终边与角的终边关于直线y=x对称,且
α∈(-4π,4π),则α= .
3.
4.
若角α的终边在如图所示的阴影部分(包括边界),
则角α的取值范围是( )
A. B.
C. D.
用弧度制表示区域角应关注的三点
1.用弧度表示区域角,必要时需进行角度与弧度的换算,注意单位要统一.
2.在表示角的集合时,可以先写出一周范围内的角(如-π~π,0~2π),再加上2kπ,k∈Z.
3.终边在同一条直线上的角的集合可以表示为{x|x=α+kπ,k∈Z};终边在相互垂直的两条直线上的角的集合可以表示为.
解题归纳
四 与弧长、扇形面积有关的问题
例4
(1)[2019·广东珠海模拟]已知扇形的周长是4 cm,则扇形面积最大时,扇形的圆心角的弧度数是( )
A.2 B.1 C. D.3
(2)[2019·广西贺州高二检测]已知扇形的圆心角为,面积为,则扇形的弧长等于 .
【解析】 (1)设扇形的半径为R cm,则弧长l=(4-2R)cm,
∴ 扇形面积S=lR=R(2-R)=-R2+2R=-(R-1)2+1.
当R=1时,S最大,此时l=2,扇形圆心角为2弧度.
(2)设扇形的半径为r,弧长为l,则解得
【答案】 (1)A (2)
【方法点拨】
1.已知圆心角的度量单位为角度制时,可直接使用角度制下扇形的弧长和面积公式:(1)弧长公式:l=;(2)面积公式:=.
2.已知圆心角的度量单位为弧度制时,可使用弧度制下扇形的弧长和面积公式:
(1)弧长公式:l=αr;
(2)面积公式:=lr=|α|r2.
解题归纳
训练题
[2020·黑龙江大庆市第十中学高一期末]已知扇形的半径为2,圆心角为2弧度,则该扇形的面积为 .
1.
2.
[2020·安徽省太和县第一中学高一期末]已知一扇形的面积是8 cm2,周长是12 cm,则该扇形的圆心角α(0<α<π)的弧度数是 .
使用弧度制下扇形的弧长和面积公式应注意
①在扇形的弧长公式与面积公式中,各含有三个量,因此可知二求一;
②使用公式时,注意角α的单位只能是弧度,而不是角度;
③弧度制下扇形面积公式S=lr,类似于三角形面识公式S=ah(其中h是三角形中长度为a的边上的高),可类比记忆.
解题归纳
小结
1.角度与弧度的换算
2.弧长公式、扇形面积公式
角度制 弧度制
弧长 公式 = =|α|r
扇形 面积 公式 = =
知易行难,重在行动
千里之行,始于足下
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
