4.3.1 公式法 课件(共16张PPT)
文档属性
| 名称 | 4.3.1 公式法 课件(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-18 00:00:00 | ||
图片预览






文档简介
(共16张PPT)
第四章 因式分解
3.1 公式法
1.探索并运用平方差公式进行因式分解,体会转化思想.(重点)
2.能会综合运用提公因式法和平方差公式对多项式进行因式分解.(难点)
学习目标
a米
b米
b米
a米
(a-b)
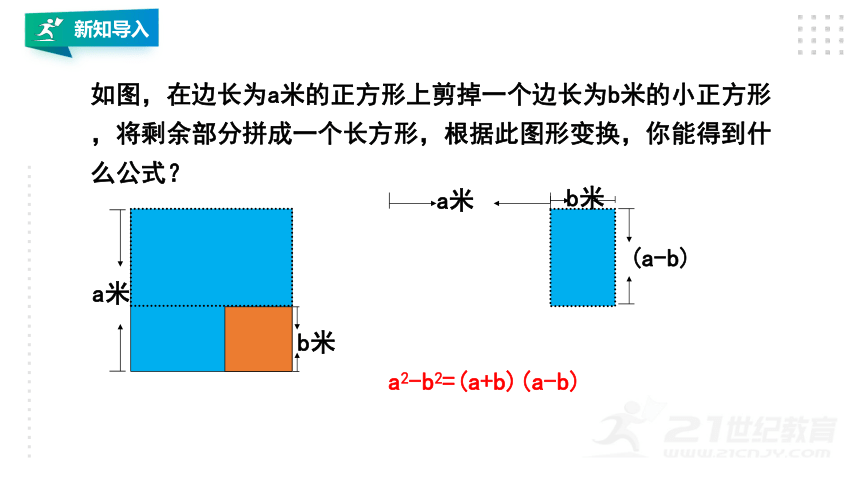
如图,在边长为a米的正方形上剪掉一个边长为b米的小正方形,将剩余部分拼成一个长方形,根据此图形变换,你能得到什么公式?
a2-b2=(a+b)(a-b)
新知导入
(1)(x+5)(x-5)=____________
(2)(3x-y)(3x+y)=___________
(3)(1+3a)(1-3a)=___________
1-9a2
x2-25
9x2-y2
它们的结果有什么共同特征?
合作探究
(1)下列多项式中,他们有什么共同特征
①x2-25
②9x2-y2
(2)尝试将它们分别写成两个因式的乘积,并与同伴交流.
(整式乘法)
(因式分解)
合作探究
事实上,把乘法公式(a+b)(a-b) = a2-b2反过来就得到
a2-b2 =(a+b)(a-b)
语言叙述:两个数的平方差,等于这两个数的和与这两个数的差的积.
合作探究
例1.把下列各式因式分解:
(1)25 - 16x2;
(2)9a2 – b2.
解: (1) 25-16x2 = 52–(4x)2 = (5+4x)(5-4x);
(2) 9a2 - b2 =(3a)2–( b)2 = (3a+ b)(3a- b).
新知讲解
方法总结:公式中的a、b无论表示数、单项式、还是多项式,只要被分解的多项式能转化成平方差的形式,就能用平方差公式因式分解.
利用平方差公式分解两项式的一般步骤:
1.找出公式中的a、b;
2.转化成a2-b2的形式;
3.根据公式a2-b2=(a+b) (a-b)写出结果.
合作探究入
例2.分解因式:
(1) 2x3-8x; (2)9(m+n)2-(m-n)2.
=(2m+4n)(4m+2n)
(2)原式=(3m+3n-m+n)(3m+3n+m-n)
=4(m+2n)(2m+n).
若用平方差公式分解后的结果中有公因式,一定要再用提公因式法继续分解.
(1)原式=2x(x2-4)
=2x(x2-22)
=2x(x+2)(x-2)
分解因式时,一般先用提公因式法进行分解,然后再用公式法.最后进行检查.
新知讲解
例3.已知x2-y2=-2,x+y=1,求x-y,x,y的值.
∴x-y=-2②.
解:∵x2-y2=(x+y)(x-y)=-2,
x+y=1①,
联立①②组成二元一次方程组,
解得
新知讲解
1.下列各式中,能用平方差公式分解因式的是( )
A.a2+b2 B.-a2+b2
C.-a2-b2 D.-(-a2)+b2
课堂练习
B
2.下列各式中,可用平方差公式分解因式的有( )
①-a2-b2;②16x2-9y2;③(-a)2-(-b)2;
④-121m2+225n2;⑤(6x)2-9(2y)2.
A.5个 B.4个 C.3个 D.2个
课堂练习
B
3.已知a,b,c为△ABC的三边长,且满足a2c2-b2c2=a4-b4,则△ABC的形状为( )
A.等腰三角形 B.直角三角形
C.等腰直角三角形 D.等腰三角形或直角三角形
课堂练习
D
1.利用平方差公式分解因式:.
2.因式分解的步骤是:首先提取公因式,然后考虑用公式法.
3.因式分解应进行到每一个因式不能分解为止.
课堂小结
https://www.21cnjy.com/help/help_extract.php
第四章 因式分解
3.1 公式法
1.探索并运用平方差公式进行因式分解,体会转化思想.(重点)
2.能会综合运用提公因式法和平方差公式对多项式进行因式分解.(难点)
学习目标
a米
b米
b米
a米
(a-b)
如图,在边长为a米的正方形上剪掉一个边长为b米的小正方形,将剩余部分拼成一个长方形,根据此图形变换,你能得到什么公式?
a2-b2=(a+b)(a-b)
新知导入
(1)(x+5)(x-5)=____________
(2)(3x-y)(3x+y)=___________
(3)(1+3a)(1-3a)=___________
1-9a2
x2-25
9x2-y2
它们的结果有什么共同特征?
合作探究
(1)下列多项式中,他们有什么共同特征
①x2-25
②9x2-y2
(2)尝试将它们分别写成两个因式的乘积,并与同伴交流.
(整式乘法)
(因式分解)
合作探究
事实上,把乘法公式(a+b)(a-b) = a2-b2反过来就得到
a2-b2 =(a+b)(a-b)
语言叙述:两个数的平方差,等于这两个数的和与这两个数的差的积.
合作探究
例1.把下列各式因式分解:
(1)25 - 16x2;
(2)9a2 – b2.
解: (1) 25-16x2 = 52–(4x)2 = (5+4x)(5-4x);
(2) 9a2 - b2 =(3a)2–( b)2 = (3a+ b)(3a- b).
新知讲解
方法总结:公式中的a、b无论表示数、单项式、还是多项式,只要被分解的多项式能转化成平方差的形式,就能用平方差公式因式分解.
利用平方差公式分解两项式的一般步骤:
1.找出公式中的a、b;
2.转化成a2-b2的形式;
3.根据公式a2-b2=(a+b) (a-b)写出结果.
合作探究入
例2.分解因式:
(1) 2x3-8x; (2)9(m+n)2-(m-n)2.
=(2m+4n)(4m+2n)
(2)原式=(3m+3n-m+n)(3m+3n+m-n)
=4(m+2n)(2m+n).
若用平方差公式分解后的结果中有公因式,一定要再用提公因式法继续分解.
(1)原式=2x(x2-4)
=2x(x2-22)
=2x(x+2)(x-2)
分解因式时,一般先用提公因式法进行分解,然后再用公式法.最后进行检查.
新知讲解
例3.已知x2-y2=-2,x+y=1,求x-y,x,y的值.
∴x-y=-2②.
解:∵x2-y2=(x+y)(x-y)=-2,
x+y=1①,
联立①②组成二元一次方程组,
解得
新知讲解
1.下列各式中,能用平方差公式分解因式的是( )
A.a2+b2 B.-a2+b2
C.-a2-b2 D.-(-a2)+b2
课堂练习
B
2.下列各式中,可用平方差公式分解因式的有( )
①-a2-b2;②16x2-9y2;③(-a)2-(-b)2;
④-121m2+225n2;⑤(6x)2-9(2y)2.
A.5个 B.4个 C.3个 D.2个
课堂练习
B
3.已知a,b,c为△ABC的三边长,且满足a2c2-b2c2=a4-b4,则△ABC的形状为( )
A.等腰三角形 B.直角三角形
C.等腰直角三角形 D.等腰三角形或直角三角形
课堂练习
D
1.利用平方差公式分解因式:.
2.因式分解的步骤是:首先提取公因式,然后考虑用公式法.
3.因式分解应进行到每一个因式不能分解为止.
课堂小结
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
