4.3.2 公式法 课件(共17张PPT)
文档属性
| 名称 | 4.3.2 公式法 课件(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-18 10:41:26 | ||
图片预览





文档简介
(共17张PPT)
第四章 因式分解
3.2 公式法
1.理解用完全平方公式进行因式分解,并能熟练地运用完全平方公式分解因式.(重点)
2.能综合运用提公因式法和完全平方公式对多项式进行因式分解.(难点)
学习目标
1.因式分解:
把一个多项式转化为几个整式的积的形式.
2.我们已经学过哪些因式分解的方法?
1.提公因式法
2.平方差公式
a2-b2=(a+b)(a-b)
新知导入
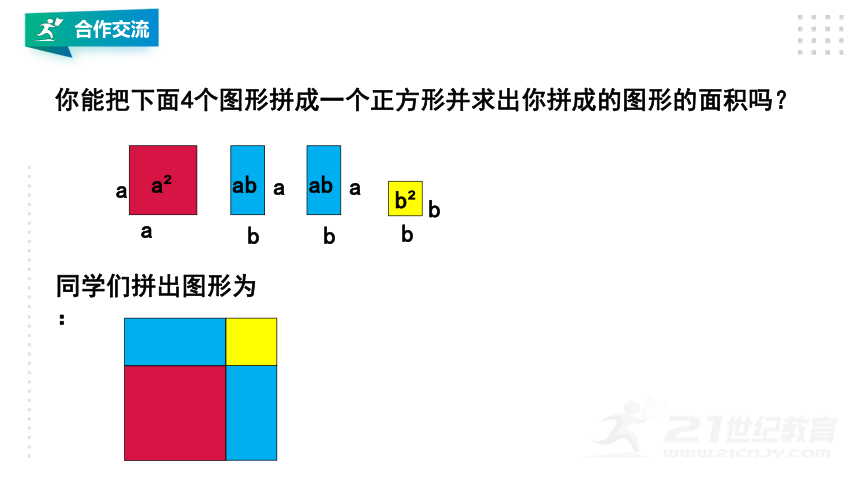
你能把下面4个图形拼成一个正方形并求出你拼成的图形的面积吗?
同学们拼出图形为:
a
a
b
b
a
b
a
b
ab
a
b
ab
合作交流
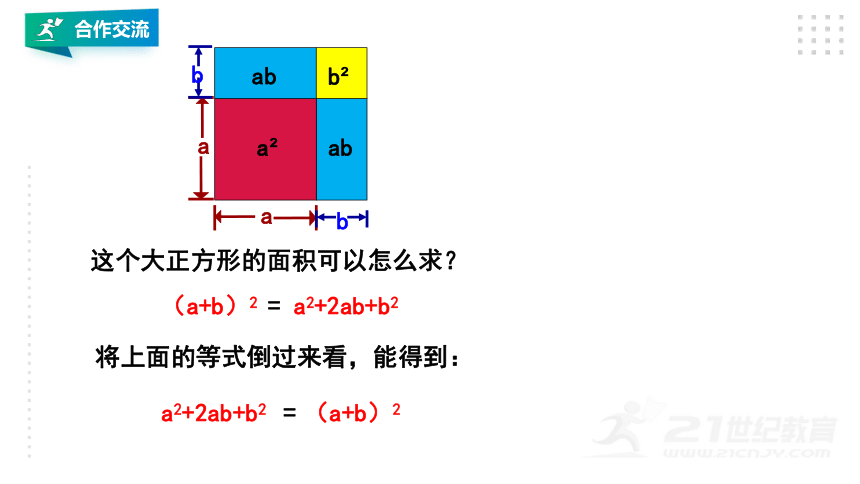
这个大正方形的面积可以怎么求?
a2+2ab+b2
(a+b)2
=
a
b
a
b
a
ab
ab
b
(a+b)2
a2+2ab+b2
=
将上面的等式倒过来看,能得到:
合作交流
a2+2ab+b2
a2-2ab+b2
我们把a +2ab+b 和a -2ab+b 这样的式子叫作完全平方式.
观察这两个式子:
(1)每个多项式有几项?
(3)中间项和第一项,第三项有什么关系?
(2)每个多项式的第一项和第三项有什么特征?
三项
这两项都是数或式的平方,并且符号相同
是第一项和第三项底数的积的±2倍
合作交流
根据因式分解与整式乘法的关系,我们可以利用乘法公式把某些多项式因式分解,这种因式分解的方法叫做公式法.
(a+b)2=a2+2ab+b2,
(a-b)2=a2-2ab+b2.
整式乘法
因式分解
a2+2ab+b2 =(a+b)2
a2-2ab+b2 =(a-b)2
合作交流
例1.把下列完全平方式因式分解:
(1)x2+14x+49;
(2)(m+n)2–6(m+n)+9.
解(1)x2+14x+49
=x2+2×7x+72
=(x+7)2;
(2)(m+n)2 –6(m+n)+9
= [(m+n)-3]2
= (m+n-3)2.
完全平方式的特点:
(1)是一个三项式;
(2)三项中有两项是两式的平方和,另一项是这两式乘积的2倍.
新知讲解
例2.把下列各式因式分解:
(1)3ax2 + 6axy + 3ay2;
(2)– x2 – 4y2 + 4xy.
解(1)3ax2 + 6axy + 3ay2
=3a(x2 +2xy+y2)
=3a(x + y)2;
(2)- x2 - 4y2 + 4xy
=-(x2 +4y2-4xy)
= - (x2 - 4xy + 4y2)
= - [x2 -2·x·2y+(2y)2]
= - (x - 2y)2.
首项有“负号”要先提
新知讲解
例3.计算或化简下列各式:
(1)2022+202×196+982;
(2)(a2-2)2-2a2(a2-2)+a4.
新知讲解
(1)原式=2022+2×202×98+982
=(202+98)2
=3002=90 000.
(2)原式=(a2-2)2-2a2(a2-2)+(a2)2
=(a2-2-a2)2
=(-2)2=4.
新知讲解
1.下列各式能用完全平方公式进行因式分解的是( )
A.x2+1 B.x2+2x-1
C.x2+x+1 D.x2+4x+4
课堂练习
D
2.把2xy-x2-y2因式分解,结果正确的是( )
A.(x-y)2 B.(-x-y)2
C.-(x-y)2 D.-(x+y)2
课堂练习
C
3.如果x2 + mxy + 9y2是一个完全平方式,那么m的值为( )
A. 6 B. ±6
C. 3 D. ±3
课堂练习
B
完全平方公式分解因式
公式
a2±2ab+b2=(a±b)2
特点
(1)要求多项式有三项.
(2)其中两项同号,且都可以写成某数或式的平方,另一项则是这两数或式的乘积的2倍,符号可正可负.
课堂小结
https://www.21cnjy.com/help/help_extract.php
第四章 因式分解
3.2 公式法
1.理解用完全平方公式进行因式分解,并能熟练地运用完全平方公式分解因式.(重点)
2.能综合运用提公因式法和完全平方公式对多项式进行因式分解.(难点)
学习目标
1.因式分解:
把一个多项式转化为几个整式的积的形式.
2.我们已经学过哪些因式分解的方法?
1.提公因式法
2.平方差公式
a2-b2=(a+b)(a-b)
新知导入
你能把下面4个图形拼成一个正方形并求出你拼成的图形的面积吗?
同学们拼出图形为:
a
a
b
b
a
b
a
b
ab
a
b
ab
合作交流
这个大正方形的面积可以怎么求?
a2+2ab+b2
(a+b)2
=
a
b
a
b
a
ab
ab
b
(a+b)2
a2+2ab+b2
=
将上面的等式倒过来看,能得到:
合作交流
a2+2ab+b2
a2-2ab+b2
我们把a +2ab+b 和a -2ab+b 这样的式子叫作完全平方式.
观察这两个式子:
(1)每个多项式有几项?
(3)中间项和第一项,第三项有什么关系?
(2)每个多项式的第一项和第三项有什么特征?
三项
这两项都是数或式的平方,并且符号相同
是第一项和第三项底数的积的±2倍
合作交流
根据因式分解与整式乘法的关系,我们可以利用乘法公式把某些多项式因式分解,这种因式分解的方法叫做公式法.
(a+b)2=a2+2ab+b2,
(a-b)2=a2-2ab+b2.
整式乘法
因式分解
a2+2ab+b2 =(a+b)2
a2-2ab+b2 =(a-b)2
合作交流
例1.把下列完全平方式因式分解:
(1)x2+14x+49;
(2)(m+n)2–6(m+n)+9.
解(1)x2+14x+49
=x2+2×7x+72
=(x+7)2;
(2)(m+n)2 –6(m+n)+9
= [(m+n)-3]2
= (m+n-3)2.
完全平方式的特点:
(1)是一个三项式;
(2)三项中有两项是两式的平方和,另一项是这两式乘积的2倍.
新知讲解
例2.把下列各式因式分解:
(1)3ax2 + 6axy + 3ay2;
(2)– x2 – 4y2 + 4xy.
解(1)3ax2 + 6axy + 3ay2
=3a(x2 +2xy+y2)
=3a(x + y)2;
(2)- x2 - 4y2 + 4xy
=-(x2 +4y2-4xy)
= - (x2 - 4xy + 4y2)
= - [x2 -2·x·2y+(2y)2]
= - (x - 2y)2.
首项有“负号”要先提
新知讲解
例3.计算或化简下列各式:
(1)2022+202×196+982;
(2)(a2-2)2-2a2(a2-2)+a4.
新知讲解
(1)原式=2022+2×202×98+982
=(202+98)2
=3002=90 000.
(2)原式=(a2-2)2-2a2(a2-2)+(a2)2
=(a2-2-a2)2
=(-2)2=4.
新知讲解
1.下列各式能用完全平方公式进行因式分解的是( )
A.x2+1 B.x2+2x-1
C.x2+x+1 D.x2+4x+4
课堂练习
D
2.把2xy-x2-y2因式分解,结果正确的是( )
A.(x-y)2 B.(-x-y)2
C.-(x-y)2 D.-(x+y)2
课堂练习
C
3.如果x2 + mxy + 9y2是一个完全平方式,那么m的值为( )
A. 6 B. ±6
C. 3 D. ±3
课堂练习
B
完全平方公式分解因式
公式
a2±2ab+b2=(a±b)2
特点
(1)要求多项式有三项.
(2)其中两项同号,且都可以写成某数或式的平方,另一项则是这两数或式的乘积的2倍,符号可正可负.
课堂小结
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
