沪科版数学七年级下册 8.1 积的乘方 课件(13张ppt)
文档属性
| 名称 | 沪科版数学七年级下册 8.1 积的乘方 课件(13张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-18 23:21:08 | ||
图片预览





文档简介
(共15张PPT)
8.1.3 积的乘方
同底数幂相乘,底数不变,指数相加。 am·an=am+n ( m、n都为正整数)
幂的乘方,底数不变,指数相乘。
(am)n=amn (m,n都是正整数)
复习引入新课:
1、计算(1) (2) (y3)4
(1)
(2)
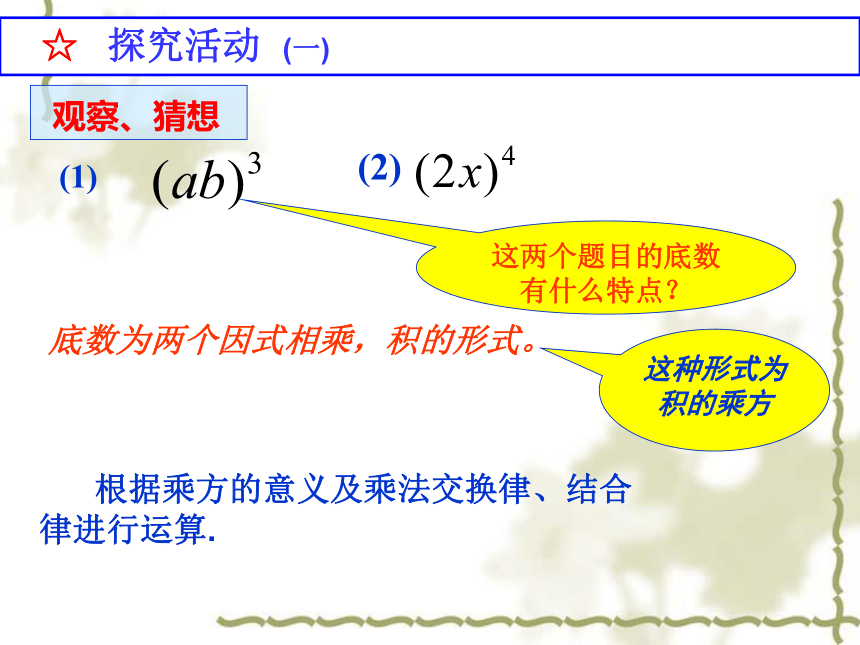
这两个题目的底数有什么特点?
底数为两个因式相乘,积的形式。
这种形式为积的乘方
☆ 探究活动 (一)
观察、猜想
根据乘方的意义及乘法交换律、结合律进行运算.
同理:
(乘方的意义)
(乘法交换律、结合律)
(乘方的意义)
=(2m).(2m).(2m).(2m)
=(2×2×2×2).(m.m.m.m.)
=24m4=16m4
(2m)4
思考: (ab)n =
(ab)n =( ab)·(ab)·……·(ab )
=(a·a·……·a) (b·b·……·b)
=an·bn
n个ab
n个a
n个b
(n为正整数)
积的乘方,等于各因式乘方的积
拓展 当三个或三个以上因式的积的乘方时, 也具有这一性质 例如 :(abc)n=anbncn n为正整数
1、口答
(1)(ab)6; (2)(-a)3;
(3)(- 2x)2 ; (4)( ab)3
(5)(-xy)7; (6)(-3abc)2;
1
2
2、计算:
(-4mn)3 (- xyz)4
1
3
a6b6
-a3
4x2
1
8
a3b3
-x7y7
9a2b2c2
-64m3n3
1
81
x4y4z4
3、下面的计算对不对?如果不对,应怎样改正?
(1)(ab2)2=ab4; (2)(3cd)3=9c3d3;
(3)(-3a3)2= -9a6; (4)(- x3y)3= - x6y3; (5)(a3+b2)3=a9+b6
4、填空: (1) a6y3=( )3;
(2)81x4y10=( )2
(3)若(a3ym)2=any8, 则m= , n= .
1
3
1
9
例题:
(1) a3 ·a4· a+(a2)4+(-2a4)2
(2) 2(x3)2 · x3-(3x3)3+(5x)2 ·x7
注意:运算顺序是先乘方,再乘除,
最后算加减。
拓展训练
(5)若n是正整数,且 ,求 的值。
5.计算:
(1)410 × 0.2510
(2) 5 × 5
看谁本领大!
(3 7 × 22
小结:
1、本节课的主要内容:
幂的运算的三个性质:
am·an=am+n (am)n=amn (ab)n=anbn ( m、n都为正整数)
2、 运用积的乘方法则时要注意什么?
每一个因式都要“乘方”,还有符号问题。
积的乘方
8.1.3 积的乘方
同底数幂相乘,底数不变,指数相加。 am·an=am+n ( m、n都为正整数)
幂的乘方,底数不变,指数相乘。
(am)n=amn (m,n都是正整数)
复习引入新课:
1、计算(1) (2) (y3)4
(1)
(2)
这两个题目的底数有什么特点?
底数为两个因式相乘,积的形式。
这种形式为积的乘方
☆ 探究活动 (一)
观察、猜想
根据乘方的意义及乘法交换律、结合律进行运算.
同理:
(乘方的意义)
(乘法交换律、结合律)
(乘方的意义)
=(2m).(2m).(2m).(2m)
=(2×2×2×2).(m.m.m.m.)
=24m4=16m4
(2m)4
思考: (ab)n =
(ab)n =( ab)·(ab)·……·(ab )
=(a·a·……·a) (b·b·……·b)
=an·bn
n个ab
n个a
n个b
(n为正整数)
积的乘方,等于各因式乘方的积
拓展 当三个或三个以上因式的积的乘方时, 也具有这一性质 例如 :(abc)n=anbncn n为正整数
1、口答
(1)(ab)6; (2)(-a)3;
(3)(- 2x)2 ; (4)( ab)3
(5)(-xy)7; (6)(-3abc)2;
1
2
2、计算:
(-4mn)3 (- xyz)4
1
3
a6b6
-a3
4x2
1
8
a3b3
-x7y7
9a2b2c2
-64m3n3
1
81
x4y4z4
3、下面的计算对不对?如果不对,应怎样改正?
(1)(ab2)2=ab4; (2)(3cd)3=9c3d3;
(3)(-3a3)2= -9a6; (4)(- x3y)3= - x6y3; (5)(a3+b2)3=a9+b6
4、填空: (1) a6y3=( )3;
(2)81x4y10=( )2
(3)若(a3ym)2=any8, 则m= , n= .
1
3
1
9
例题:
(1) a3 ·a4· a+(a2)4+(-2a4)2
(2) 2(x3)2 · x3-(3x3)3+(5x)2 ·x7
注意:运算顺序是先乘方,再乘除,
最后算加减。
拓展训练
(5)若n是正整数,且 ,求 的值。
5.计算:
(1)410 × 0.2510
(2) 5 × 5
看谁本领大!
(3 7 × 22
小结:
1、本节课的主要内容:
幂的运算的三个性质:
am·an=am+n (am)n=amn (ab)n=anbn ( m、n都为正整数)
2、 运用积的乘方法则时要注意什么?
每一个因式都要“乘方”,还有符号问题。
积的乘方
