沪科版数学七年级下册 8.3 完全平方公式与平方差公式 第1课时 表格式教案
文档属性
| 名称 | 沪科版数学七年级下册 8.3 完全平方公式与平方差公式 第1课时 表格式教案 |
|
|
| 格式 | docx | ||
| 文件大小 | 53.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-19 10:47:06 | ||
图片预览



文档简介
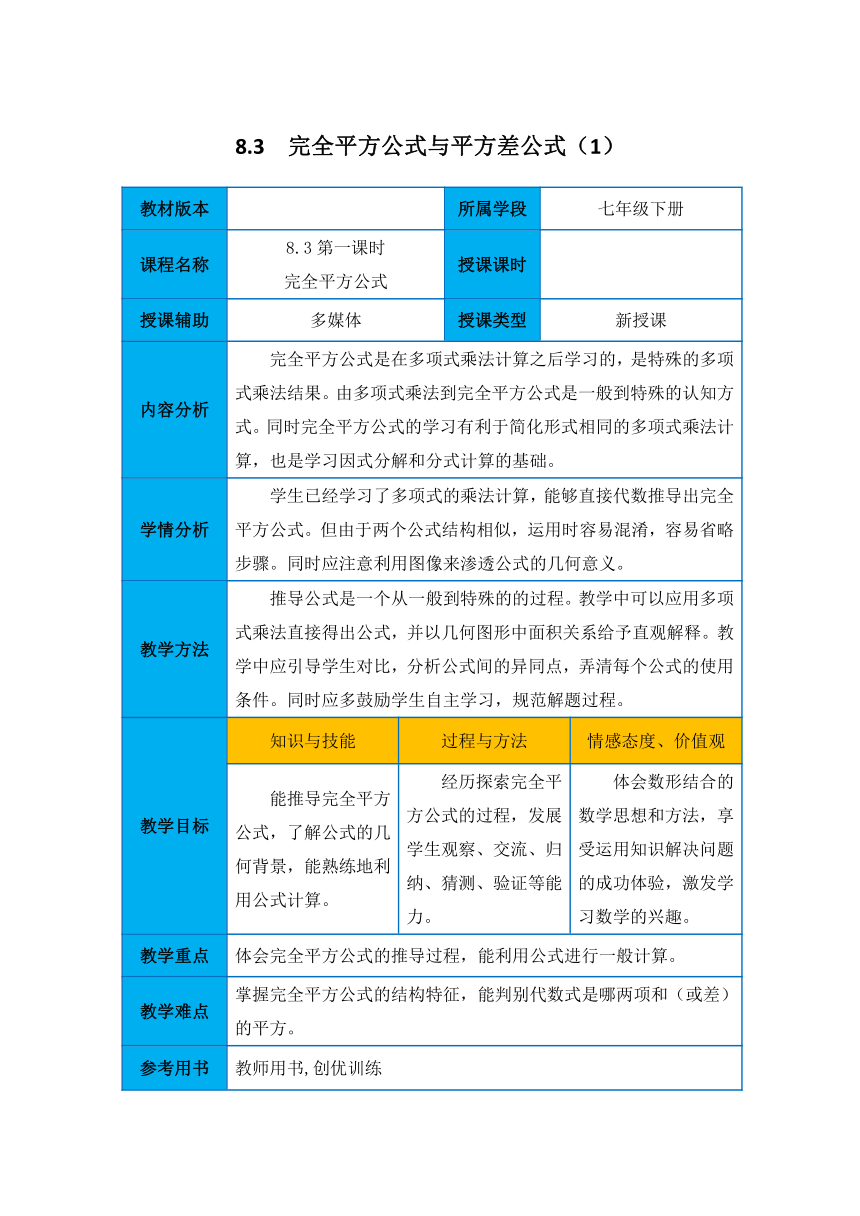
8.3 完全平方公式与平方差公式(1)
教材版本 所属学段 七年级下册
课程名称 8.3第一课时 完全平方公式 授课课时
授课辅助 多媒体 授课类型 新授课
内容分析 完全平方公式是在多项式乘法计算之后学习的,是特殊的多项式乘法结果。由多项式乘法到完全平方公式是一般到特殊的认知方式。同时完全平方公式的学习有利于简化形式相同的多项式乘法计算,也是学习因式分解和分式计算的基础。
学情分析 学生已经学习了多项式的乘法计算,能够直接代数推导出完全平方公式。但由于两个公式结构相似,运用时容易混淆,容易省略步骤。同时应注意利用图像来渗透公式的几何意义。
教学方法 推导公式是一个从一般到特殊的的过程。教学中可以应用多项式乘法直接得出公式,并以几何图形中面积关系给予直观解释。教学中应引导学生对比,分析公式间的异同点,弄清每个公式的使用条件。同时应多鼓励学生自主学习,规范解题过程。
教学目标 知识与技能 过程与方法 情感态度、价值观
能推导完全平方公式,了解公式的几何背景,能熟练地利用公式计算。 经历探索完全平方公式的过程,发展学生观察、交流、归纳、猜测、验证等能力。 体会数形结合的数学思想和方法,享受运用知识解决问题的成功体验,激发学习数学的兴趣。
教学重点 体会完全平方公式的推导过程,能利用公式进行一般计算。
教学难点 掌握完全平方公式的结构特征,能判别代数式是哪两项和(或差)的平方。
参考用书 教师用书,创优训练
教 学过程设计 教 学 过 程 设 计
教 学 环 节 师 生 活 动 设 计 意 图
一、探索感悟 1、用多项式乘法计算下列练习。 (1)(x+3) (2)(x-3) (3m+2n) (3m-2n) () (a-5) (m+n) (m-n) 2、你发现两组计算有何规律? 用自己的语言表述出来 教师活动:给出两组计算,并提出问题 学生活动:自主完成两组计算,并把两组结果相比较,找出异同,表述发现。 利用多项式乘法计算导入,既让学生体会到完全平方公式是特殊的多项式乘法计算,又通过两组计算形成鲜明对比,利于学生理解两个公式的不同。
二、讲授新知 1、你能猜想一下(a+b) 和 (a-b) 的结果吗? 并验证你的结论 2、用自己的语言叙述你的猜想。 教师活动:提出问题 学生活动: 猜想并验证 (a+b) =a +2ab+b (a-b) =a -2ab+b 教师活动: 板书完全平方公式 学生活动: 两个数的和(或差)的平方,等于这两个数的平方和加(或减)这两个数乘积的2倍。 学生经历猜想、验证,归纳总结出公式。师生共同明确公式结构,便于对公式更好地理解。
教 学过程设计 教 学 过 程 设 计
教 学 环 节 师 生 活 动 设 计 意 图
三、几何验证 观察:完全平方公式,除了直接由乘法得到,你还可通过图形面积割补的方法得到吗? (a+b)2=a2+2ab+( ) 图(1) (a-b)2=a2-( )+b2 图(2) 教师活动:引导学生利用面积恒等来解决问题 学生活动: 图(1) 整体:(a+b) 部分和:a +2ab+b 相等: (a+b) =a +2ab+b 图(2) (a-b) =a -2ab+b 利用图形直观地说明完全平方公式的几何意义,加深对公式的理解,并体会数形结合的思想方法。
四、例题讲解 例1利用完全平方公式计算: (1)(2x+y)2; (2)(3a-2b) 解: 教师活动:运用公式计算,要先识别a,b在具体式子中分别表示什么。 学生活动:学生指出题目中a,b分别对应哪一项 例1利用箭头,直观的指出a,b分别在代数式中对应哪一项,利于学生更好的理解和掌握公式。
教 学过程设计 教 学 过 程 设 计
教 学 环 节 师 生 活 动 设 计 意 图
例2利用完全平方公式简算。 (1)101 (2)98 教师活动: 学生活动: (1)101 =(100+1) =10 +2×100×1+1 =10000+200+1 =10201 (2)98 =(100-2) =100 -2×100×2+2 =10000-400+4 =9604 例2将完全平方公式与简便计算相结合,在巩固的基础上有所提升。
五、巩固练习 1、填空 (1)(a+ ) =a +4ab+4b (2)(x- ) = -6xy+ (3) [ + ] =4x + +9y 2、利用乘法公式计算: (1)(3x+1) (2) (2x+) 3、利用完全平方公式简算: (1)97 (2) 102. 4、如图,是一张正方形的纸片,如果把它沿着各边都剪去3cm宽的一条,那么所得小正方形的面积比原正方形的面 教师活动:练习1的(1)、(2)让学生独立完成,(3)引导学生发散思维,答案不唯一 练习2,3可以学生黑板板书 学生活动: (1)找准题目中对应的a,b。 (2)练习1的(3)尝试给出不同的答案。 练习1考察学生对公式的理解。 练习2,3巩固并检测对公式的掌握程度。
教 学过程设计 教 学 过 程 设 计
教 学 环 节 师 生 活 动 设 计 意 图
积比原正方形的面积减少84cm ,求原正方形的边长. 教师活动:数形结合 学生活动: 设原正方形的边长为xcm.则 x -(x-6) =84. 12x-36=84. x=10. ∴原正方形的边长为10cm. 练习4有关图形的应用题,进一步体会数形结合的思想。
六、自主小结 请同学们说说今天你有什么收获? 教师活动:鼓励学生主动发言。 学生活动:经过思考和讨论后,分享自己的收获。 让学生自己回顾、梳理知识,利于学生知识的自我建构和思维严谨性的培养。
七、作业设置 1、必做作业 书本习题8.3第1题 基础训练8.3(一) 2、选做作业 (1)已知a+b=10,ab=21,求下列各式的值. (1)a +b (2) (a-b) 分层设计作业,使不同层级的学生得到不同程度的发展。
板书设计 8.3完全平方公式与平方差公式(1) 1、完全平方公式 2、几何验证 (a+b) =a +2ab+b (a-b) =a -2ab+b 3、例题讲解 4、巩固练习 5、自主小结
教学反思 从多项式乘法计算引出完全平方公式,学生在教师的引导下经历计算、猜想、验证等过程,体会由一般到特殊,数与形相结合的数学思想。同时,学生积极主动参与教学活动,体验学习知识,应用知识的成就感,增强学习数学的兴趣和信心。
教材版本 所属学段 七年级下册
课程名称 8.3第一课时 完全平方公式 授课课时
授课辅助 多媒体 授课类型 新授课
内容分析 完全平方公式是在多项式乘法计算之后学习的,是特殊的多项式乘法结果。由多项式乘法到完全平方公式是一般到特殊的认知方式。同时完全平方公式的学习有利于简化形式相同的多项式乘法计算,也是学习因式分解和分式计算的基础。
学情分析 学生已经学习了多项式的乘法计算,能够直接代数推导出完全平方公式。但由于两个公式结构相似,运用时容易混淆,容易省略步骤。同时应注意利用图像来渗透公式的几何意义。
教学方法 推导公式是一个从一般到特殊的的过程。教学中可以应用多项式乘法直接得出公式,并以几何图形中面积关系给予直观解释。教学中应引导学生对比,分析公式间的异同点,弄清每个公式的使用条件。同时应多鼓励学生自主学习,规范解题过程。
教学目标 知识与技能 过程与方法 情感态度、价值观
能推导完全平方公式,了解公式的几何背景,能熟练地利用公式计算。 经历探索完全平方公式的过程,发展学生观察、交流、归纳、猜测、验证等能力。 体会数形结合的数学思想和方法,享受运用知识解决问题的成功体验,激发学习数学的兴趣。
教学重点 体会完全平方公式的推导过程,能利用公式进行一般计算。
教学难点 掌握完全平方公式的结构特征,能判别代数式是哪两项和(或差)的平方。
参考用书 教师用书,创优训练
教 学过程设计 教 学 过 程 设 计
教 学 环 节 师 生 活 动 设 计 意 图
一、探索感悟 1、用多项式乘法计算下列练习。 (1)(x+3) (2)(x-3) (3m+2n) (3m-2n) () (a-5) (m+n) (m-n) 2、你发现两组计算有何规律? 用自己的语言表述出来 教师活动:给出两组计算,并提出问题 学生活动:自主完成两组计算,并把两组结果相比较,找出异同,表述发现。 利用多项式乘法计算导入,既让学生体会到完全平方公式是特殊的多项式乘法计算,又通过两组计算形成鲜明对比,利于学生理解两个公式的不同。
二、讲授新知 1、你能猜想一下(a+b) 和 (a-b) 的结果吗? 并验证你的结论 2、用自己的语言叙述你的猜想。 教师活动:提出问题 学生活动: 猜想并验证 (a+b) =a +2ab+b (a-b) =a -2ab+b 教师活动: 板书完全平方公式 学生活动: 两个数的和(或差)的平方,等于这两个数的平方和加(或减)这两个数乘积的2倍。 学生经历猜想、验证,归纳总结出公式。师生共同明确公式结构,便于对公式更好地理解。
教 学过程设计 教 学 过 程 设 计
教 学 环 节 师 生 活 动 设 计 意 图
三、几何验证 观察:完全平方公式,除了直接由乘法得到,你还可通过图形面积割补的方法得到吗? (a+b)2=a2+2ab+( ) 图(1) (a-b)2=a2-( )+b2 图(2) 教师活动:引导学生利用面积恒等来解决问题 学生活动: 图(1) 整体:(a+b) 部分和:a +2ab+b 相等: (a+b) =a +2ab+b 图(2) (a-b) =a -2ab+b 利用图形直观地说明完全平方公式的几何意义,加深对公式的理解,并体会数形结合的思想方法。
四、例题讲解 例1利用完全平方公式计算: (1)(2x+y)2; (2)(3a-2b) 解: 教师活动:运用公式计算,要先识别a,b在具体式子中分别表示什么。 学生活动:学生指出题目中a,b分别对应哪一项 例1利用箭头,直观的指出a,b分别在代数式中对应哪一项,利于学生更好的理解和掌握公式。
教 学过程设计 教 学 过 程 设 计
教 学 环 节 师 生 活 动 设 计 意 图
例2利用完全平方公式简算。 (1)101 (2)98 教师活动: 学生活动: (1)101 =(100+1) =10 +2×100×1+1 =10000+200+1 =10201 (2)98 =(100-2) =100 -2×100×2+2 =10000-400+4 =9604 例2将完全平方公式与简便计算相结合,在巩固的基础上有所提升。
五、巩固练习 1、填空 (1)(a+ ) =a +4ab+4b (2)(x- ) = -6xy+ (3) [ + ] =4x + +9y 2、利用乘法公式计算: (1)(3x+1) (2) (2x+) 3、利用完全平方公式简算: (1)97 (2) 102. 4、如图,是一张正方形的纸片,如果把它沿着各边都剪去3cm宽的一条,那么所得小正方形的面积比原正方形的面 教师活动:练习1的(1)、(2)让学生独立完成,(3)引导学生发散思维,答案不唯一 练习2,3可以学生黑板板书 学生活动: (1)找准题目中对应的a,b。 (2)练习1的(3)尝试给出不同的答案。 练习1考察学生对公式的理解。 练习2,3巩固并检测对公式的掌握程度。
教 学过程设计 教 学 过 程 设 计
教 学 环 节 师 生 活 动 设 计 意 图
积比原正方形的面积减少84cm ,求原正方形的边长. 教师活动:数形结合 学生活动: 设原正方形的边长为xcm.则 x -(x-6) =84. 12x-36=84. x=10. ∴原正方形的边长为10cm. 练习4有关图形的应用题,进一步体会数形结合的思想。
六、自主小结 请同学们说说今天你有什么收获? 教师活动:鼓励学生主动发言。 学生活动:经过思考和讨论后,分享自己的收获。 让学生自己回顾、梳理知识,利于学生知识的自我建构和思维严谨性的培养。
七、作业设置 1、必做作业 书本习题8.3第1题 基础训练8.3(一) 2、选做作业 (1)已知a+b=10,ab=21,求下列各式的值. (1)a +b (2) (a-b) 分层设计作业,使不同层级的学生得到不同程度的发展。
板书设计 8.3完全平方公式与平方差公式(1) 1、完全平方公式 2、几何验证 (a+b) =a +2ab+b (a-b) =a -2ab+b 3、例题讲解 4、巩固练习 5、自主小结
教学反思 从多项式乘法计算引出完全平方公式,学生在教师的引导下经历计算、猜想、验证等过程,体会由一般到特殊,数与形相结合的数学思想。同时,学生积极主动参与教学活动,体验学习知识,应用知识的成就感,增强学习数学的兴趣和信心。
