湖南省师大附中2013届高三第5次月考数学(文)试题
文档属性
| 名称 | 湖南省师大附中2013届高三第5次月考数学(文)试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 224.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-02-28 00:00:00 | ||
图片预览

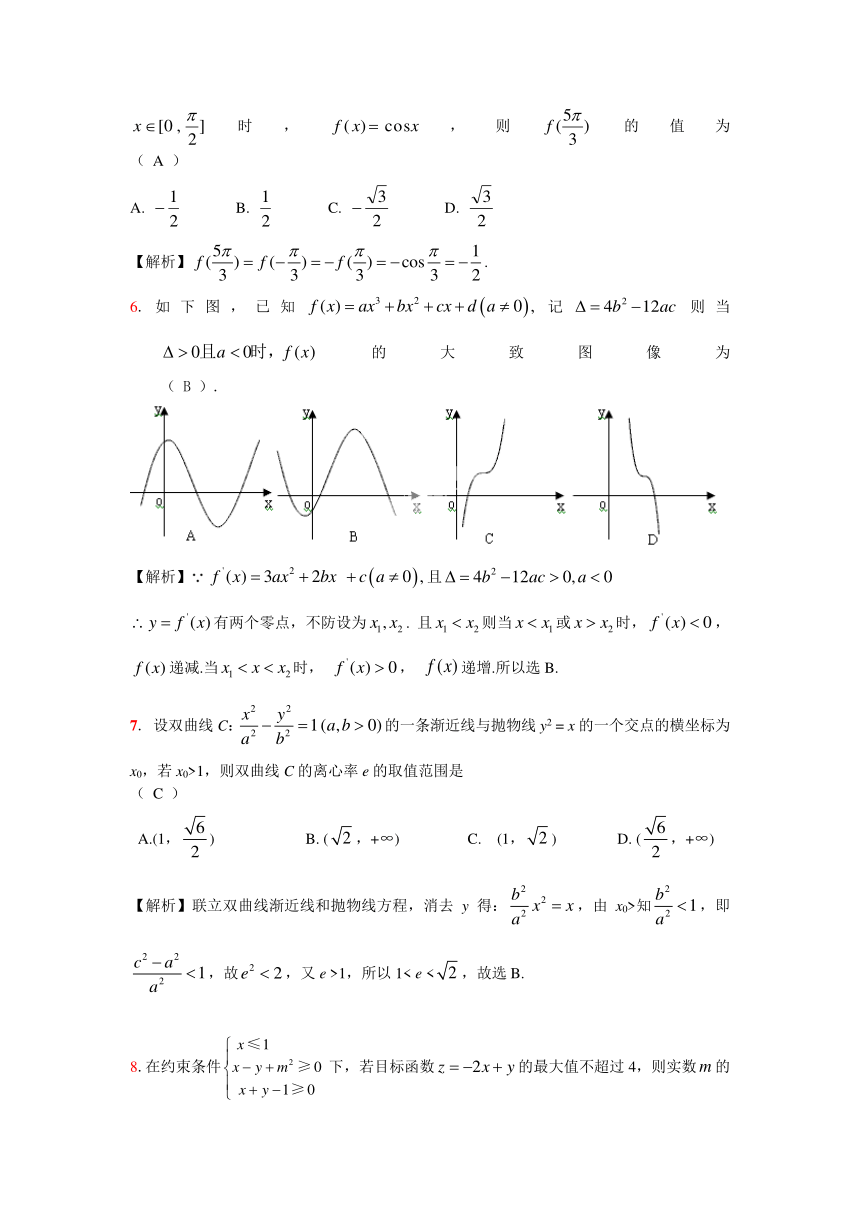



文档简介
湖南省师大附中2013届高三第5次月考
数学(文)试题
命题:曾克平 洪利民 苏萍 审题:湖南师大附中高三数学文科备课组
(考试范围:高中文科数学全部内容)
一.选择题:本大题共9小题,每小题5分,共45分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 设集合, ,则= ( A )
A. B. C. D.
【解析】利用数轴易知选A.
2.等差数列中,,,则 ( C )
A.16 B.21 C.20 D.31
【解析】由,可求得.
3.给出如下四个命题:
① 若“且”为假命题,则、均为假命题;
②若等差数列的前n项和为则三点共线;
③ “ x∈R,x2+1≥1”的否定是 “x∈R,x2+1≤1”;
④ 在中,“”是“”的充要条件.
其中正确的命题的个数是 ( D )
A.1 B. 4 C. 3 D.2
【解析】若“且”为假命题,则、至少有一个为假命题,所以①错;若等差数列的前n项和为,则数列为等差数列,所以②对;“ x∈R,x2+1≥1”的否定是 “x∈R,x2+1<1”; 所以③错;在中, “”等价于“”, 所以④对.
4. 已知平面内一点及,若,则点与的位置关系是( C )
A.点在线段上 B.点在线段上
C.点在线段上 D.点在外部
【解析】,所以C对.
5.定义在R上的函数既是奇函数又是周期函数,若的最小正周期是,且当时,,则的值为 ( A )
A. B. C. D.
【解析】.
6.如下图,已知记则当的大致图像为 ( B ).
【解析】且
有两个零点,不防设为. 且则当或时,,递减.当时, , 递增.所以选B.
7. 设双曲线C:的一条渐近线与抛物线y2 = x的一个交点的横坐标为x0,若x0>1,则双曲线C的离心率e的取值范围是 ( C )
A.(1,) B. (,+∞) C. (1,) D. (,+∞)
【解析】联立双曲线渐近线和抛物线方程,消去y得:,由x0>知,即,故,又e >1,所以1< e <,故选B.
8.在约束条件下,若目标函数的最大值不超过4,则实数的取值范围 ( D )
A B C D
【解析】作出可行域,即知目标函数在点处取得最大值.
由得
9. 已知,实数a、b、c满足<0,且0<a<b<c,若实数是函数的一个零点,那么下列不等式中,不可能成立的是 ( D )
A.<a B.>b C.<c D.>c
【解析】当时,当时
<0,且,所以不可能成立.
二.填空题:本大题共7个小题,考生作答6小题,每小题5分,共30分,把答案填在答题卡中对应题号后的横线上.
(一)选做题:从下列两题中任意选做一题,若两题全做,则只按第9题记分.
10.(坐标系与参数方程选做题)极坐标方程为的圆与参数方程为 的直线位置关系是_ _______相交_____.
【解析】.圆心(0,1)到直线的距离小于半径1.
11.(优选法选做题)下列五个函数:①,②,,③,,④,⑤中,不是单峰函数的是________.
【解析】根据单峰函数的定义知②⑤是单峰函数.
(二)必做题(11~16题)
12.定义运算,复数z满足
则复数在复平面对应点为P_(2,-1) .
【解析】设,则
即,所以在复平面对应点为P(2,-1).
13.已知,,若对,,使,则的范围 .
【解析】若对,,;使,则
当时,;当时,.
所以,由,得.
14.一个三棱锥的三视图是三个直角三角形,如图所示,则该三棱锥的外接球表面积为( A )
A.
B.
C.
D.
【解析】由三视图复原几何体,几何体是底面是直角三角形,
一条侧棱垂直底面直角顶点的三棱锥;把它扩展为长方体,两者有相同的外接球,
它的对角线的长为球的直径,即该三棱锥的外接球的表面积为:.
15.已知M是面积为1的△ABC内的一点(不含边界),,若△MBC,△MCA和△MAB的面积分别为,则的最小值是 3 .
【解析】由已知可得,
.
16.对于定义域和值域均为的函数,定义,,…,,n=1,2,3,….满足的点称为f的阶周期点.
(1)设则f的阶周期点的个数是____1_______;
(2)设则f的阶周期点的个数是____4_______ .
【解析】(1)得;
(2)当,即时,.由
得;当,即时,
由,得;同理可得另两个周期点.
三、解答题:本大题共6个小题,共75分.解答应写出文字说明、证明过程或演算步骤.
17.(本题满分12分)
已知A,B,C是的三个内角,A,B,C对的边分别为a,b,c,设平面向量,,.
(Ⅰ)求角A的值;
(Ⅱ)若,设角B的大小为,的周长为,求的最大值.
「解析」(Ⅰ),,且
,即 …………(3分) A,B,C是的三个内角,
即,又
……………………………………………………………………(6分)
(Ⅱ)由,及正弦定理得
………………………………………………(8分)
+ …………………(10分),
,即时, ………………………………………(12分)
18.(本题满分12分)
某同学利用国庆节进行社会实践,对[25,55]岁的人群随机抽取n人进行了一次生活习惯是否符合低碳生活的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
组数 分组 低碳族的人数 占本组的频率
第一组 120 0.6
第二组 195 p
第三组 100 0.5
第四组 a 0.4
第五组 30 0.3
第六组 15 0.3
(1)补全频率分布直方图,并求n,a,p的值;
(2)从年龄段在的“低碳族”中采用分层抽样抽取6人参加户外低碳体验生活,其中选取2人作为领队,求选取的2名领队中恰有1人年龄在岁的概率。
解:(1)第二组的频率为1-(0.04+0.04+0.03+0.02+0.01)×5=0.3
所以高为 ………………………………(2分)频率直方图如下:
第一组的人数为,频率为,所以
由题意可知,第二组的频率为0.3,所以第二组的人数为
第四组的频率为,所以第四组的人数为,所以 ………………………………(6分)
(2)因为岁年龄段的“低碳族”与岁年龄段的“低碳族”的比值为60:30=2:1,所以采用分层抽样法抽取6人,岁中有4人, 岁中有2人. …………(8分)
设岁中的4人为岁中的2人为,则选取2人作为领队的情况有:共15种,其中恰有1人年龄在 岁的情况有:,共8种. ……………………(11分)
所以选取的2名领队中恰有1人年龄在岁的概率为 ………………(12分)
19.(本题满分12分)
如图,三棱锥中,,,,.
(Ⅰ)证明:;
(Ⅱ)求直线AC与平面ABD所成的角的正弦值.
「解析」:(Ⅰ)在中,,,
, …………………………………………(2分)
又,且
,又
………………………………………………………………………(6分)
(Ⅱ)在三角形中,,,
,
由(1)可知:
………………………………………(8分) 在中, ,
在中,,,故
………………………………………(10分)
设点C到平面ABD的距离为h,CA与平面ABD所成的角为
即AC与平面ABD所成的角的正弦值为 ………………(12分)20.(本题满分13分)
已知单调递增的等比数列满足: ;
(1)求数列的通项公式;
(2)若,数列的前n项和为,求成立的正整数 n的最小值.
【解析】(1)设等比数列的首项为,公比为q,
依题意,有,解之得或;…………………………(4分)
又单调递增,∴,∴.………………………………………………….6分)
(2)依题意,, …………………………………………………(8分)
∴ ①,
∴ ②,
∴①-②得,
………………………………………………………………………(10分)
∴即为,
∵当n≤4时,;当n≥5时,.
∴使成立的正整数n的最小值为5. ………………………………………(13分)
21.(本题满分13分)
为了使“神州七号”飞船的返回仓顺利返回地面,及时将航天员救出,地面指挥中心在返回仓预计到达区域安排了三个救援点A、B、C(如图).其中点B在点A的正东方向,且与点A相距6km;点C在点B的北偏东30°方向,且与点B相距4km.某一时刻,返回仓于点P着陆,并同时发出着陆信号.由于B、C两地比A地距着陆点P远,因此在救援点A收到信号4s后,B、C两个救援点才同时接受到返回仓的着陆信号,已知该信号的传播速度为1km/s.
(1)试确定返回仓的着陆点P相对于救援点A的位置;
(2)若返回仓在着陆点P的正上方某处发出信号,那么救援点A与B收到信号的时间差变大还是变小?说明你的理由.
【解】(1)以AB所在直线为x轴,线段AB的垂直平分线
为y轴,建立直角坐标系,则点A(-3,0),B(3,0). ………… (2分)
过点C作x轴的垂线,垂足为D,由已知,|BC|=4,
∠CBD=60°.则|BD|=4cos60°=2,|CD|=4sin60°=,
所以C(5,). 因为|PB|=|PC|,所以点P在线段BC的垂直平分线上.
因为直线BC的斜率为tan60°=,线段BC的中点为(4,).
所以线段BC的垂直平分线方程为是,即.
因为|PB|-|PA|=4,所以点P在以A、B为焦点的
双曲线左支上,且双曲线方程为.…………(4分)
由,
即(11x-32)(x+8)=0. 因为x<0,所以x=-8,点P(-8,).过点P作x轴的垂线,垂足为E,则|AE|=5,|PE|=.所以|PA|=10,tan∠PAE=,即∠PAE=60°.
故着陆点P位于救援点A的北偏西30°,且与点A相距10km. …………(8分)
(2)设返回仓在着陆点P的正上方点M处发出信号,|PM|=h,|PA|=a,|PB|=b,如图.
则
.
故救援点A与B收到信号的时间差变小. …………………………(13分)
22. (本题满分13分)
已知函数
(1)讨论函数的单调性;
(2)若函数在处取得极值,不等式对恒成立,求实数的取值范围;
(3)当时,证明不等式
解:(1)函数的定义域是且…………………………(1分)
当时,,从而,函数在上单调递减;
当时,若,则,从而;
若,则,从而,
所以函数在上单调递减,在上单调递增. …………………(4分)
(2)由(1)可知,函数的极值点是,若,则.
若在上恒成立,即在上恒成立,只需在上恒成立. ………………………………………………(6分)
令,则,
易知为函数在内唯一的极小值点,也是最小值点,故,即=,故只要即可.
所以b的取值范围是.……………………………………………………(8分)
(3)由题意可知,要证不等式成立,只需证.
构造函数,则,因为在上单调递增,由于,所以,所以,即.
……………………………………………………………………………………………(13分)
3
4
2
左视图
主视图
俯视图
A
B
D
C
P
C
B
A
A
B
C
P
D
x
y
O
E
A
B
M
P
数学(文)试题
命题:曾克平 洪利民 苏萍 审题:湖南师大附中高三数学文科备课组
(考试范围:高中文科数学全部内容)
一.选择题:本大题共9小题,每小题5分,共45分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 设集合, ,则= ( A )
A. B. C. D.
【解析】利用数轴易知选A.
2.等差数列中,,,则 ( C )
A.16 B.21 C.20 D.31
【解析】由,可求得.
3.给出如下四个命题:
① 若“且”为假命题,则、均为假命题;
②若等差数列的前n项和为则三点共线;
③ “ x∈R,x2+1≥1”的否定是 “x∈R,x2+1≤1”;
④ 在中,“”是“”的充要条件.
其中正确的命题的个数是 ( D )
A.1 B. 4 C. 3 D.2
【解析】若“且”为假命题,则、至少有一个为假命题,所以①错;若等差数列的前n项和为,则数列为等差数列,所以②对;“ x∈R,x2+1≥1”的否定是 “x∈R,x2+1<1”; 所以③错;在中, “”等价于“”, 所以④对.
4. 已知平面内一点及,若,则点与的位置关系是( C )
A.点在线段上 B.点在线段上
C.点在线段上 D.点在外部
【解析】,所以C对.
5.定义在R上的函数既是奇函数又是周期函数,若的最小正周期是,且当时,,则的值为 ( A )
A. B. C. D.
【解析】.
6.如下图,已知记则当的大致图像为 ( B ).
【解析】且
有两个零点,不防设为. 且则当或时,,递减.当时, , 递增.所以选B.
7. 设双曲线C:的一条渐近线与抛物线y2 = x的一个交点的横坐标为x0,若x0>1,则双曲线C的离心率e的取值范围是 ( C )
A.(1,) B. (,+∞) C. (1,) D. (,+∞)
【解析】联立双曲线渐近线和抛物线方程,消去y得:,由x0>知,即,故,又e >1,所以1< e <,故选B.
8.在约束条件下,若目标函数的最大值不超过4,则实数的取值范围 ( D )
A B C D
【解析】作出可行域,即知目标函数在点处取得最大值.
由得
9. 已知,实数a、b、c满足<0,且0<a<b<c,若实数是函数的一个零点,那么下列不等式中,不可能成立的是 ( D )
A.<a B.>b C.<c D.>c
【解析】当时,当时
<0,且,所以不可能成立.
二.填空题:本大题共7个小题,考生作答6小题,每小题5分,共30分,把答案填在答题卡中对应题号后的横线上.
(一)选做题:从下列两题中任意选做一题,若两题全做,则只按第9题记分.
10.(坐标系与参数方程选做题)极坐标方程为的圆与参数方程为 的直线位置关系是_ _______相交_____.
【解析】.圆心(0,1)到直线的距离小于半径1.
11.(优选法选做题)下列五个函数:①,②,,③,,④,⑤中,不是单峰函数的是________.
【解析】根据单峰函数的定义知②⑤是单峰函数.
(二)必做题(11~16题)
12.定义运算,复数z满足
则复数在复平面对应点为P_(2,-1) .
【解析】设,则
即,所以在复平面对应点为P(2,-1).
13.已知,,若对,,使,则的范围 .
【解析】若对,,;使,则
当时,;当时,.
所以,由,得.
14.一个三棱锥的三视图是三个直角三角形,如图所示,则该三棱锥的外接球表面积为( A )
A.
B.
C.
D.
【解析】由三视图复原几何体,几何体是底面是直角三角形,
一条侧棱垂直底面直角顶点的三棱锥;把它扩展为长方体,两者有相同的外接球,
它的对角线的长为球的直径,即该三棱锥的外接球的表面积为:.
15.已知M是面积为1的△ABC内的一点(不含边界),,若△MBC,△MCA和△MAB的面积分别为,则的最小值是 3 .
【解析】由已知可得,
.
16.对于定义域和值域均为的函数,定义,,…,,n=1,2,3,….满足的点称为f的阶周期点.
(1)设则f的阶周期点的个数是____1_______;
(2)设则f的阶周期点的个数是____4_______ .
【解析】(1)得;
(2)当,即时,.由
得;当,即时,
由,得;同理可得另两个周期点.
三、解答题:本大题共6个小题,共75分.解答应写出文字说明、证明过程或演算步骤.
17.(本题满分12分)
已知A,B,C是的三个内角,A,B,C对的边分别为a,b,c,设平面向量,,.
(Ⅰ)求角A的值;
(Ⅱ)若,设角B的大小为,的周长为,求的最大值.
「解析」(Ⅰ),,且
,即 …………(3分) A,B,C是的三个内角,
即,又
……………………………………………………………………(6分)
(Ⅱ)由,及正弦定理得
………………………………………………(8分)
+ …………………(10分),
,即时, ………………………………………(12分)
18.(本题满分12分)
某同学利用国庆节进行社会实践,对[25,55]岁的人群随机抽取n人进行了一次生活习惯是否符合低碳生活的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
组数 分组 低碳族的人数 占本组的频率
第一组 120 0.6
第二组 195 p
第三组 100 0.5
第四组 a 0.4
第五组 30 0.3
第六组 15 0.3
(1)补全频率分布直方图,并求n,a,p的值;
(2)从年龄段在的“低碳族”中采用分层抽样抽取6人参加户外低碳体验生活,其中选取2人作为领队,求选取的2名领队中恰有1人年龄在岁的概率。
解:(1)第二组的频率为1-(0.04+0.04+0.03+0.02+0.01)×5=0.3
所以高为 ………………………………(2分)频率直方图如下:
第一组的人数为,频率为,所以
由题意可知,第二组的频率为0.3,所以第二组的人数为
第四组的频率为,所以第四组的人数为,所以 ………………………………(6分)
(2)因为岁年龄段的“低碳族”与岁年龄段的“低碳族”的比值为60:30=2:1,所以采用分层抽样法抽取6人,岁中有4人, 岁中有2人. …………(8分)
设岁中的4人为岁中的2人为,则选取2人作为领队的情况有:共15种,其中恰有1人年龄在 岁的情况有:,共8种. ……………………(11分)
所以选取的2名领队中恰有1人年龄在岁的概率为 ………………(12分)
19.(本题满分12分)
如图,三棱锥中,,,,.
(Ⅰ)证明:;
(Ⅱ)求直线AC与平面ABD所成的角的正弦值.
「解析」:(Ⅰ)在中,,,
, …………………………………………(2分)
又,且
,又
………………………………………………………………………(6分)
(Ⅱ)在三角形中,,,
,
由(1)可知:
………………………………………(8分) 在中, ,
在中,,,故
………………………………………(10分)
设点C到平面ABD的距离为h,CA与平面ABD所成的角为
即AC与平面ABD所成的角的正弦值为 ………………(12分)20.(本题满分13分)
已知单调递增的等比数列满足: ;
(1)求数列的通项公式;
(2)若,数列的前n项和为,求成立的正整数 n的最小值.
【解析】(1)设等比数列的首项为,公比为q,
依题意,有,解之得或;…………………………(4分)
又单调递增,∴,∴.………………………………………………….6分)
(2)依题意,, …………………………………………………(8分)
∴ ①,
∴ ②,
∴①-②得,
………………………………………………………………………(10分)
∴即为,
∵当n≤4时,;当n≥5时,.
∴使成立的正整数n的最小值为5. ………………………………………(13分)
21.(本题满分13分)
为了使“神州七号”飞船的返回仓顺利返回地面,及时将航天员救出,地面指挥中心在返回仓预计到达区域安排了三个救援点A、B、C(如图).其中点B在点A的正东方向,且与点A相距6km;点C在点B的北偏东30°方向,且与点B相距4km.某一时刻,返回仓于点P着陆,并同时发出着陆信号.由于B、C两地比A地距着陆点P远,因此在救援点A收到信号4s后,B、C两个救援点才同时接受到返回仓的着陆信号,已知该信号的传播速度为1km/s.
(1)试确定返回仓的着陆点P相对于救援点A的位置;
(2)若返回仓在着陆点P的正上方某处发出信号,那么救援点A与B收到信号的时间差变大还是变小?说明你的理由.
【解】(1)以AB所在直线为x轴,线段AB的垂直平分线
为y轴,建立直角坐标系,则点A(-3,0),B(3,0). ………… (2分)
过点C作x轴的垂线,垂足为D,由已知,|BC|=4,
∠CBD=60°.则|BD|=4cos60°=2,|CD|=4sin60°=,
所以C(5,). 因为|PB|=|PC|,所以点P在线段BC的垂直平分线上.
因为直线BC的斜率为tan60°=,线段BC的中点为(4,).
所以线段BC的垂直平分线方程为是,即.
因为|PB|-|PA|=4,所以点P在以A、B为焦点的
双曲线左支上,且双曲线方程为.…………(4分)
由,
即(11x-32)(x+8)=0. 因为x<0,所以x=-8,点P(-8,).过点P作x轴的垂线,垂足为E,则|AE|=5,|PE|=.所以|PA|=10,tan∠PAE=,即∠PAE=60°.
故着陆点P位于救援点A的北偏西30°,且与点A相距10km. …………(8分)
(2)设返回仓在着陆点P的正上方点M处发出信号,|PM|=h,|PA|=a,|PB|=b,如图.
则
.
故救援点A与B收到信号的时间差变小. …………………………(13分)
22. (本题满分13分)
已知函数
(1)讨论函数的单调性;
(2)若函数在处取得极值,不等式对恒成立,求实数的取值范围;
(3)当时,证明不等式
解:(1)函数的定义域是且…………………………(1分)
当时,,从而,函数在上单调递减;
当时,若,则,从而;
若,则,从而,
所以函数在上单调递减,在上单调递增. …………………(4分)
(2)由(1)可知,函数的极值点是,若,则.
若在上恒成立,即在上恒成立,只需在上恒成立. ………………………………………………(6分)
令,则,
易知为函数在内唯一的极小值点,也是最小值点,故,即=,故只要即可.
所以b的取值范围是.……………………………………………………(8分)
(3)由题意可知,要证不等式成立,只需证.
构造函数,则,因为在上单调递增,由于,所以,所以,即.
……………………………………………………………………………………………(13分)
3
4
2
左视图
主视图
俯视图
A
B
D
C
P
C
B
A
A
B
C
P
D
x
y
O
E
A
B
M
P
同课章节目录
