2021-2022学年度北师大版九年级数学下册 1.3 三角函数的计算 课件(共20张)
文档属性
| 名称 | 2021-2022学年度北师大版九年级数学下册 1.3 三角函数的计算 课件(共20张) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-19 13:16:12 | ||
图片预览






文档简介
(共20张PPT)
第一章
直角三角形的边角关系
1.3 三角函数的计算
授课人:XXXX
九年级数学北师版·下册
教学目标
1.经历用计算器由已知锐角求三角函数的过程,进一步体会三角函数的意义.
2.能够运用计算器辅助解决含三角函数值计算的实际问题,提高用现代工具解决实际问题的能力.
3.发现实际问题中的边角关系,提高学生有条理地思考和表达的能力.
新课导入
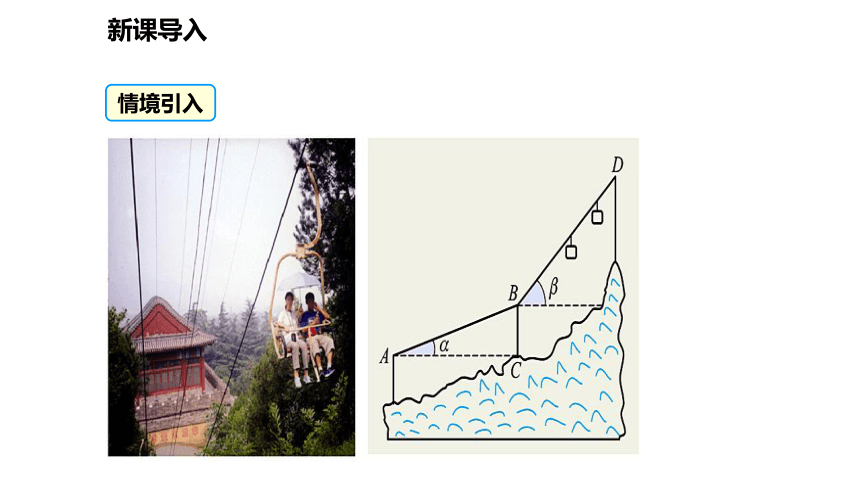
情境引入
新课导入
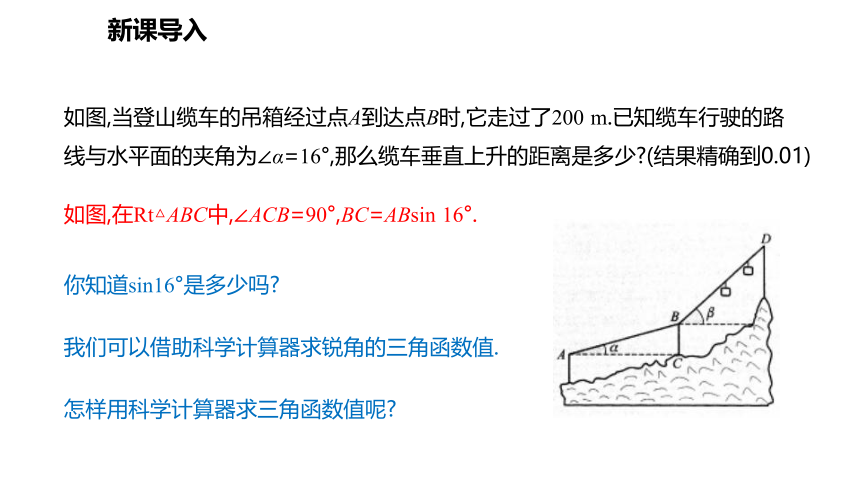
如图,当登山缆车的吊箱经过点A到达点B时,它走过了200 m.已知缆车行驶的路线与水平面的夹角为∠α=16°,那么缆车垂直上升的距离是多少 (结果精确到0.01)
你知道sin16°是多少吗
我们可以借助科学计算器求锐角的三角函数值.
怎样用科学计算器求三角函数值呢
如图,在Rt△ABC中,∠ACB=90°,BC=ABsin 16°.
新课导入
用科学计算器求三角函数值,要用到三个键:
例如,求sin16°,cos42°,tan85°和sin72°38′25″的按键顺序如下表所示:
sin
cos
tan
按键顺序
sin 16°
cos 42°
tan 85°
sin 72° 38′25″
sin
1
6
cos
4
2
tan
8
5
sin
7
2
3
8
2
5
=
=
=
=
由于计算器的型号与功能不同,请按照相应的说明书使用.
新知探究
对于本节一开始提出的问题,利用科学计算器可以求得: BC=ABsin16°≈200×0.275 6=55.12(m).
当缆车继续从点B到达点D时,它又走过了200 m.缆车由点B到点D的行驶路线与水平面的夹角为∠β=42°,由此你还能计算什么
温馨提示:用计算器求三角函数值时,结果一般有10个数位.本书约定,如无特别说明,计算结果一般精确到万分位.
缆车从B点运动到D点,垂直上升的距离是多少?
BDsin42°≈200×0.6691=133.83(m).
新知探究
1、用计算器求下列各式的值:
(1)sin 56°.
(2)sin 15°49′.
(3)cos 20°.
(4)tan 29°.
(5)tan 44°59′59″.
(6)sin 15°+cos 61°+tan 76°.
【跟踪训练】
新知探究
解:
(1)0.8290,
(2)0.2726,
(3)0.9397,
(4)0.5543,
(5)1.0000,
(6)4.7544 .
新知探究
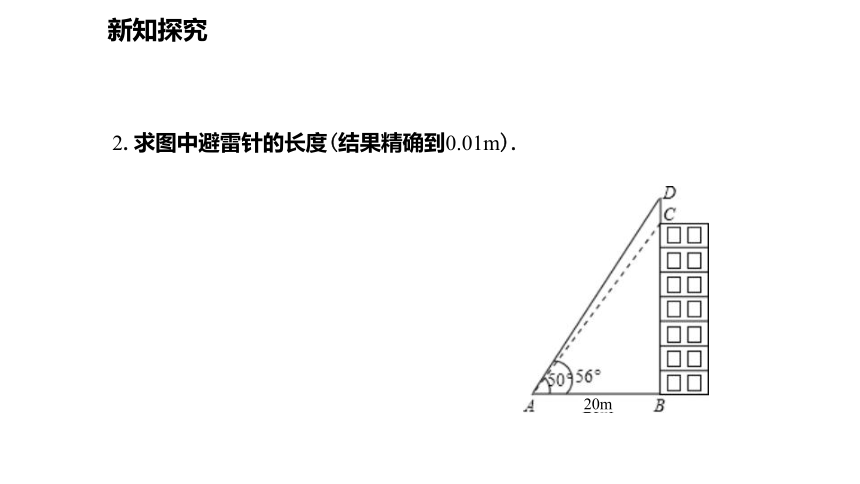
2.求图中避雷针的长度(结果精确到0.01m).
20m
新知探究
解:在Rt△ABC中,
在Rt△ABD中,
tan
tan
20tan
tan
tan
20tan
20tan
20tan50
(m) .
新知探究
温馨提示:当从低处观察高处的目标时.视线与水平线所成的锐角称为仰角.当从高处观察低处的目标时.视线与水平线所成的锐角称为俯角.
A
O
B
C
3.如图,物华大厦离小伟家60m,小伟从自家的窗中眺望大厦,并测得大厦顶部的仰角是45°,而大厦底部的俯角是37°,求该大厦的高度 (结果精确到0.1m).
新知探究
A
O
B
C
解:如图,在Rt△AOC中,
在Rt△BOC中,
答:物华大厦的高度约为105.2m.
60tan
tan
tan
tan
tan
60tan
60tan
60tan
(m) .
课堂小结
1.运用计算器计算已知锐角的三角函数值.
2.运用计算器辅助解决含三角函数值计算的实际问题.
通过本课时的学习,需要我们掌握:
课堂小测
1.在△ABC中,∠C=90°, ∠A=72°,AB=10,则边AC的长约为(精确到0.1)( )
A.9.1 B.9.5 C.3.1 D.3.5
【解析】AC=ABcos72°≈10×0.309≈3.1.
C
课堂小测
2. 光明中学九(1)班开展数学实践活动,小李沿着东西方向的公路以50 m/min的速度向正东方向行走,在A处测得建筑物C在北偏东60°方向上,20 min后他走到B处,测得建筑物C在北偏西45°方向上,求建筑物C到公路AB的距离.( )
课堂小测
解:过点C作CD⊥AB于D点,由题意可知AB=50×20=1000 m,
答:建筑物C到公路AB的距离约为366 m.
D
B
60°
∠CAB=30°,∠CBA=45°,AD= ,BD= ,
tan
tan
∵AD+BD = =1000(m),
tan
tan
m
m
课堂小测
3. 目前世界上最高的电视塔是广州新电视塔.如图所示,新电视塔高AB为610米,远处有一栋大楼,某人在楼底C处测得塔顶B的仰角为45°,在楼顶D处测得塔顶B的仰角为39°.
(1)求大楼与电视塔之间的距离AC.
(2)求大楼的高度CD(精确到1米).
课堂小测
答:大楼的高度CD约为116米.
解:(1)由题意,AC=AB=610 米.
故BE=DEtan39°.
因为CD=AE,所以CD=AB-DE·tan 39°
=610-610×tan 39°≈116(米).
(2)DE=AC=610米,
在Rt△BDE中,tan∠BDE=
课堂小测
【规律方法】
解决此类实际问题的关键是能够根据题意画出几何图形,构造直角三角形,充分利用三角函数的有关知识并能结合勾股定理灵活运用.
第一章
直角三角形的边角关系
1.3 三角函数的计算
授课人:XXXX
九年级数学北师版·下册
教学目标
1.经历用计算器由已知锐角求三角函数的过程,进一步体会三角函数的意义.
2.能够运用计算器辅助解决含三角函数值计算的实际问题,提高用现代工具解决实际问题的能力.
3.发现实际问题中的边角关系,提高学生有条理地思考和表达的能力.
新课导入
情境引入
新课导入
如图,当登山缆车的吊箱经过点A到达点B时,它走过了200 m.已知缆车行驶的路线与水平面的夹角为∠α=16°,那么缆车垂直上升的距离是多少 (结果精确到0.01)
你知道sin16°是多少吗
我们可以借助科学计算器求锐角的三角函数值.
怎样用科学计算器求三角函数值呢
如图,在Rt△ABC中,∠ACB=90°,BC=ABsin 16°.
新课导入
用科学计算器求三角函数值,要用到三个键:
例如,求sin16°,cos42°,tan85°和sin72°38′25″的按键顺序如下表所示:
sin
cos
tan
按键顺序
sin 16°
cos 42°
tan 85°
sin 72° 38′25″
sin
1
6
cos
4
2
tan
8
5
sin
7
2
3
8
2
5
=
=
=
=
由于计算器的型号与功能不同,请按照相应的说明书使用.
新知探究
对于本节一开始提出的问题,利用科学计算器可以求得: BC=ABsin16°≈200×0.275 6=55.12(m).
当缆车继续从点B到达点D时,它又走过了200 m.缆车由点B到点D的行驶路线与水平面的夹角为∠β=42°,由此你还能计算什么
温馨提示:用计算器求三角函数值时,结果一般有10个数位.本书约定,如无特别说明,计算结果一般精确到万分位.
缆车从B点运动到D点,垂直上升的距离是多少?
BDsin42°≈200×0.6691=133.83(m).
新知探究
1、用计算器求下列各式的值:
(1)sin 56°.
(2)sin 15°49′.
(3)cos 20°.
(4)tan 29°.
(5)tan 44°59′59″.
(6)sin 15°+cos 61°+tan 76°.
【跟踪训练】
新知探究
解:
(1)0.8290,
(2)0.2726,
(3)0.9397,
(4)0.5543,
(5)1.0000,
(6)4.7544 .
新知探究
2.求图中避雷针的长度(结果精确到0.01m).
20m
新知探究
解:在Rt△ABC中,
在Rt△ABD中,
tan
tan
20tan
tan
tan
20tan
20tan
20tan50
(m) .
新知探究
温馨提示:当从低处观察高处的目标时.视线与水平线所成的锐角称为仰角.当从高处观察低处的目标时.视线与水平线所成的锐角称为俯角.
A
O
B
C
3.如图,物华大厦离小伟家60m,小伟从自家的窗中眺望大厦,并测得大厦顶部的仰角是45°,而大厦底部的俯角是37°,求该大厦的高度 (结果精确到0.1m).
新知探究
A
O
B
C
解:如图,在Rt△AOC中,
在Rt△BOC中,
答:物华大厦的高度约为105.2m.
60tan
tan
tan
tan
tan
60tan
60tan
60tan
(m) .
课堂小结
1.运用计算器计算已知锐角的三角函数值.
2.运用计算器辅助解决含三角函数值计算的实际问题.
通过本课时的学习,需要我们掌握:
课堂小测
1.在△ABC中,∠C=90°, ∠A=72°,AB=10,则边AC的长约为(精确到0.1)( )
A.9.1 B.9.5 C.3.1 D.3.5
【解析】AC=ABcos72°≈10×0.309≈3.1.
C
课堂小测
2. 光明中学九(1)班开展数学实践活动,小李沿着东西方向的公路以50 m/min的速度向正东方向行走,在A处测得建筑物C在北偏东60°方向上,20 min后他走到B处,测得建筑物C在北偏西45°方向上,求建筑物C到公路AB的距离.( )
课堂小测
解:过点C作CD⊥AB于D点,由题意可知AB=50×20=1000 m,
答:建筑物C到公路AB的距离约为366 m.
D
B
60°
∠CAB=30°,∠CBA=45°,AD= ,BD= ,
tan
tan
∵AD+BD = =1000(m),
tan
tan
m
m
课堂小测
3. 目前世界上最高的电视塔是广州新电视塔.如图所示,新电视塔高AB为610米,远处有一栋大楼,某人在楼底C处测得塔顶B的仰角为45°,在楼顶D处测得塔顶B的仰角为39°.
(1)求大楼与电视塔之间的距离AC.
(2)求大楼的高度CD(精确到1米).
课堂小测
答:大楼的高度CD约为116米.
解:(1)由题意,AC=AB=610 米.
故BE=DEtan39°.
因为CD=AE,所以CD=AB-DE·tan 39°
=610-610×tan 39°≈116(米).
(2)DE=AC=610米,
在Rt△BDE中,tan∠BDE=
课堂小测
【规律方法】
解决此类实际问题的关键是能够根据题意画出几何图形,构造直角三角形,充分利用三角函数的有关知识并能结合勾股定理灵活运用.
