2021-2022学年度人教版九年级数学下册 27.2.1.1平行线分线段成比例课件(共18张PPT)
文档属性
| 名称 | 2021-2022学年度人教版九年级数学下册 27.2.1.1平行线分线段成比例课件(共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-19 16:14:01 | ||
图片预览



文档简介
(共18张PPT)
第二十七章
27.2相似三角形
九年级数学人教版·下册
27.2.1.1平行线分线段成比例
授课人:XXXX
教学目标
1.掌握平行线分线段成比例基本事实;(重点)
2.能利用平行线判定三角形相似.(难点)
新课导入
1. 对应角_______, 对应边 的两个
三角形, 叫做相似三角形.
2. 相似三角形的 , 各对应边 .
相等
成比例
对应角相等
成比例
复习回顾
A
B
C
A1
B1
C1
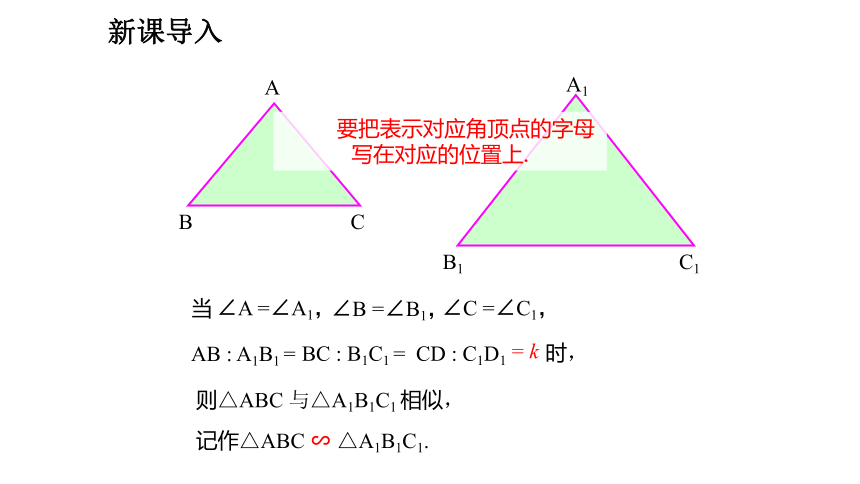
∠A =∠A1,
∠B =∠B1,
∠C =∠C1,
AB : A1B1 =
BC : B1C1 =
CD : C1D1
= k
当
时,
则△ABC 与△A1B1C1 相似,
记作△ABC ∽ △A1B1C1.
要把表示对应角顶点的字母写在对应的位置上.
新课导入
新课导入
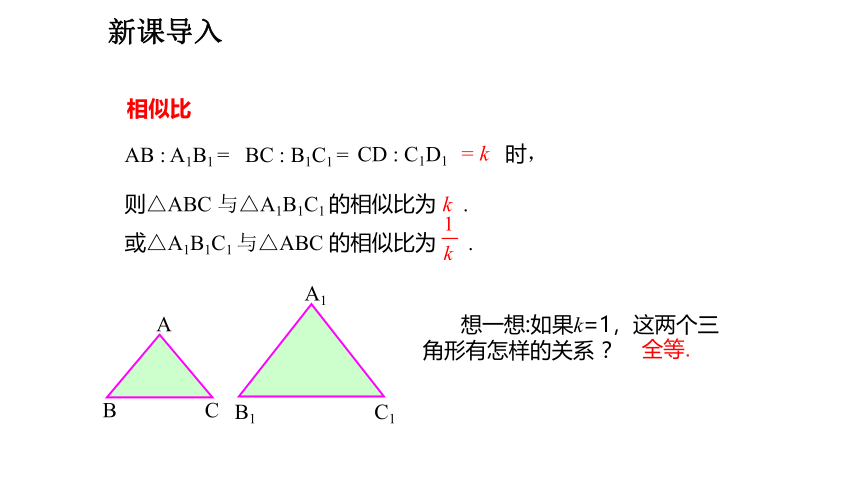
相似比
AB : A1B1 =
BC : B1C1 =
CD : C1D1
= k
时,
A
B
C
A1
B1
C1
则△ABC 与△A1B1C1 的相似比为 k .
或△A1B1C1 与△ABC 的相似比为 .
想一想:如果k=1,这两个三角形有怎样的关系 ?
全等.
新知探究
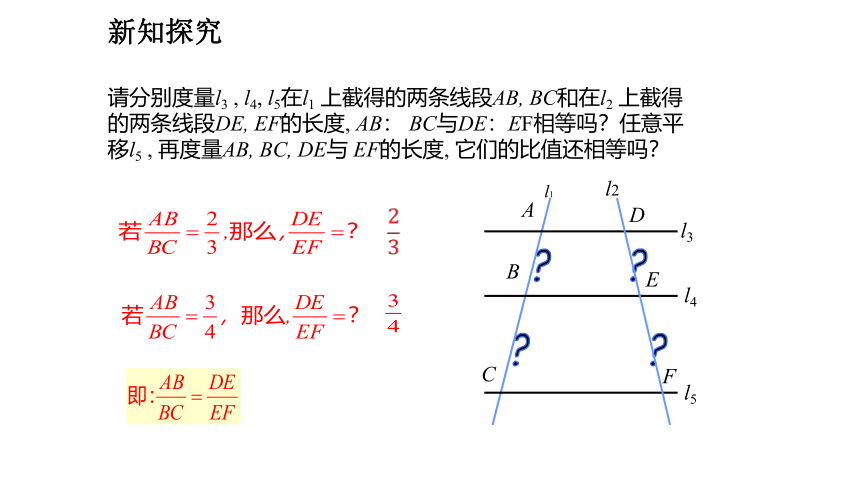
请分别度量l3 , l4, l5在l1 上截得的两条线段AB, BC和在l2 上截得的两条线段DE, EF的长度, AB: BC与DE:EF相等吗?任意平移l5 , 再度量AB, BC, DE与 EF的长度, 它们的比值还相等吗?
A
B
C
D
E
F
l3
l4
l5
l1
l2
新知探究
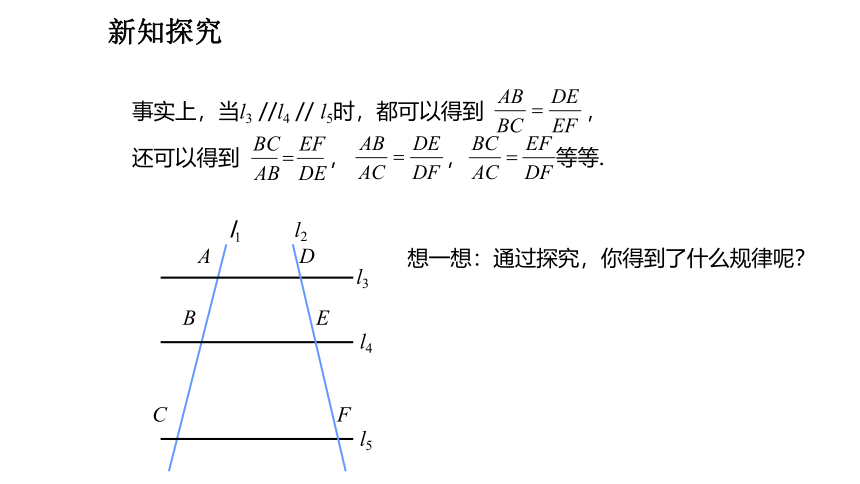
事实上,当l3 //l4 // l5时,都可以得到 , 还可以得到 , , 等等.
A
B
C
D
E
F
l3
l4
l5
l1
l2
想一想:通过探究,你得到了什么规律呢?
新知探究
平行线分线段成比例的基本事实:三条平行线截两条直线,所得到的对应线段的比相等.
把平行线分线段成比例的事实应用到三角形,会出现以下两种情况:
B
A
C
A
B
C
平移
新知探究
新知探究
平行于三角形一边的直线截其它两边(或两边的延长线),
所得的对应线段成比例.
新知探究
思考:
如图,在△ABC中,DE∥BC,且DE分别交AB,AC于点D,E, △ADE与△ABC有什么关系?
A
D
B
C
E
F
证明:∵ DE∥BC,
∴∠ADE=∠B, ∠AED=∠C.
过点E作为EF∥AB,交BC于F.
∵ DE∥BC, EF∥AB,
∴ .
∵四边形DBFE是平行四边形,
∴DE=BF.
又∵∠A=∠A, ∴△ADE∽△ABC.
.
.
新知探究
要熟悉该基本事实的几种基本图形
A
B
C
D
E
F
A
B
C
D
E
F
新知探究
注意该定理在三角形中的应用
新知探究
平行于三角形的一边的直线和其它两边相交,所构成的三角形与原三角形相似.
课堂小结
平行线分线段成比例
平行线分线段成比例的基本事实:三条平行线截两条直线,所得到的对应线段的比相等.
平行于三角形一边的直线截其它两边(或两边的延长线),所得的对应线段成比例.
课堂小测
1.平行于三角形一边的直线与其它两边(或延长线)相交,所得的三角形与原三角形________.
(图2)
D
E
O
B
C
A
B
C
D
E
(图1)
相似
课堂小测
2.如图所示,如果D,E,F分别在OA,OB,OC上,
且DF∥AC,EF∥BC.求证:
证明: ∵ DF∥AC,
∵EF∥BC,
第二十七章
27.2相似三角形
九年级数学人教版·下册
27.2.1.1平行线分线段成比例
授课人:XXXX
教学目标
1.掌握平行线分线段成比例基本事实;(重点)
2.能利用平行线判定三角形相似.(难点)
新课导入
1. 对应角_______, 对应边 的两个
三角形, 叫做相似三角形.
2. 相似三角形的 , 各对应边 .
相等
成比例
对应角相等
成比例
复习回顾
A
B
C
A1
B1
C1
∠A =∠A1,
∠B =∠B1,
∠C =∠C1,
AB : A1B1 =
BC : B1C1 =
CD : C1D1
= k
当
时,
则△ABC 与△A1B1C1 相似,
记作△ABC ∽ △A1B1C1.
要把表示对应角顶点的字母写在对应的位置上.
新课导入
新课导入
相似比
AB : A1B1 =
BC : B1C1 =
CD : C1D1
= k
时,
A
B
C
A1
B1
C1
则△ABC 与△A1B1C1 的相似比为 k .
或△A1B1C1 与△ABC 的相似比为 .
想一想:如果k=1,这两个三角形有怎样的关系 ?
全等.
新知探究
请分别度量l3 , l4, l5在l1 上截得的两条线段AB, BC和在l2 上截得的两条线段DE, EF的长度, AB: BC与DE:EF相等吗?任意平移l5 , 再度量AB, BC, DE与 EF的长度, 它们的比值还相等吗?
A
B
C
D
E
F
l3
l4
l5
l1
l2
新知探究
事实上,当l3 //l4 // l5时,都可以得到 , 还可以得到 , , 等等.
A
B
C
D
E
F
l3
l4
l5
l1
l2
想一想:通过探究,你得到了什么规律呢?
新知探究
平行线分线段成比例的基本事实:三条平行线截两条直线,所得到的对应线段的比相等.
把平行线分线段成比例的事实应用到三角形,会出现以下两种情况:
B
A
C
A
B
C
平移
新知探究
新知探究
平行于三角形一边的直线截其它两边(或两边的延长线),
所得的对应线段成比例.
新知探究
思考:
如图,在△ABC中,DE∥BC,且DE分别交AB,AC于点D,E, △ADE与△ABC有什么关系?
A
D
B
C
E
F
证明:∵ DE∥BC,
∴∠ADE=∠B, ∠AED=∠C.
过点E作为EF∥AB,交BC于F.
∵ DE∥BC, EF∥AB,
∴ .
∵四边形DBFE是平行四边形,
∴DE=BF.
又∵∠A=∠A, ∴△ADE∽△ABC.
.
.
新知探究
要熟悉该基本事实的几种基本图形
A
B
C
D
E
F
A
B
C
D
E
F
新知探究
注意该定理在三角形中的应用
新知探究
平行于三角形的一边的直线和其它两边相交,所构成的三角形与原三角形相似.
课堂小结
平行线分线段成比例
平行线分线段成比例的基本事实:三条平行线截两条直线,所得到的对应线段的比相等.
平行于三角形一边的直线截其它两边(或两边的延长线),所得的对应线段成比例.
课堂小测
1.平行于三角形一边的直线与其它两边(或延长线)相交,所得的三角形与原三角形________.
(图2)
D
E
O
B
C
A
B
C
D
E
(图1)
相似
课堂小测
2.如图所示,如果D,E,F分别在OA,OB,OC上,
且DF∥AC,EF∥BC.求证:
证明: ∵ DF∥AC,
∵EF∥BC,
