2021-2022学年度人教版九年级数学 下册 27.2.1.2相似三角形的判定课件 (共14张PPT)
文档属性
| 名称 | 2021-2022学年度人教版九年级数学 下册 27.2.1.2相似三角形的判定课件 (共14张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-19 17:53:26 | ||
图片预览




文档简介
(共14张PPT)
第二十七章
27.2相似三角形
九年级数学人教版·下册
27.2.1.2相似三角形的判定定理1
授课人:XXXX
教学目标
1.能运用三边成比例、两边成比例且夹角相等的两个三角形相似判定定理证明三角形相似;(重点)
2.三角形相似判定定理的证明过程.(难点)
新课导入
1、两个三角形全等有哪些判定方法?
2、我们学过哪些判定三角形相似的方法?
3、全等三角形与相似三角形有怎样的关系?
SSS、SAS、ASA、AAS、HL(直角三角形)
(1)定义;(2)对应角相等,对应边的比相等.
全等三角形一定是相似三角形,相似三角形不一定是全等三角形.
新知探究
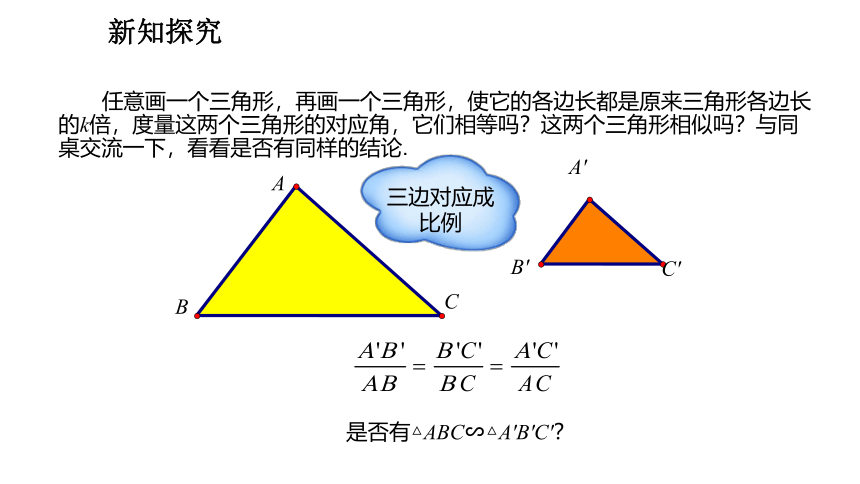
任意画一个三角形,再画一个三角形,使它的各边长都是原来三角形各边长的k倍,度量这两个三角形的对应角,它们相等吗?这两个三角形相似吗?与同桌交流一下,看看是否有同样的结论.
是否有△ABC∽△A′B′C′?
A
B
C
C′
B′
A′
三边对应成 比例
新知探究
A
B
C
D
E
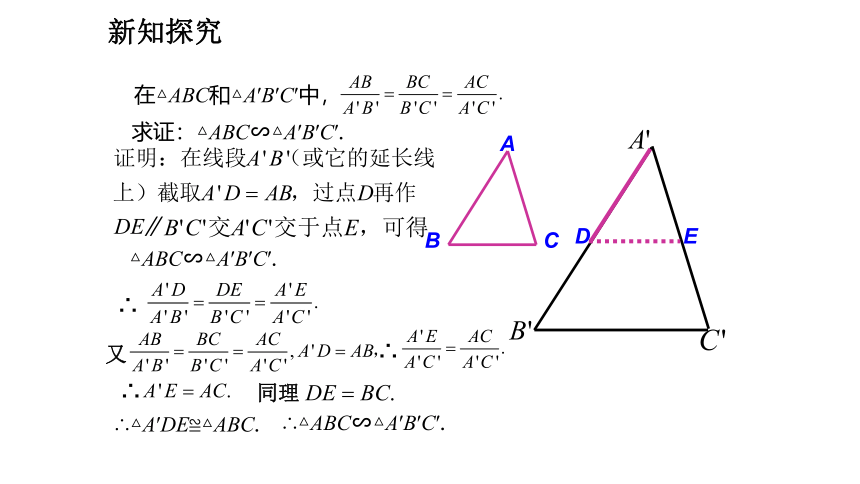
∴
又
∴
同理
∥
∴
在△ABC和△A′B′C′中,
求证:△ABC∽△A′B′C′.
△ABC∽△A′B′C′.
∴△ABC∽△A′B′C′.
∴△A′DE≌△ABC.
新知探究
A
B
C
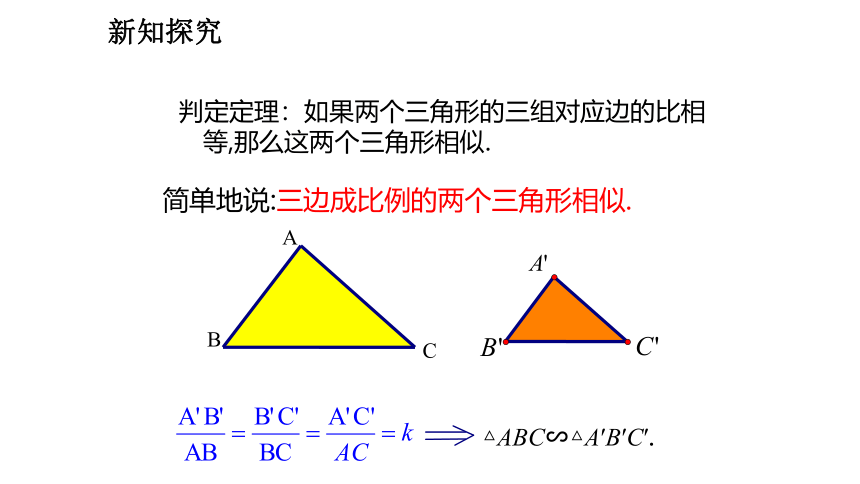
判定定理:如果两个三角形的三组对应边的比相等,那么这两个三角形相似.
简单地说:三边成比例的两个三角形相似.
△ABC∽△A′B′C′.
新知探究
例1:根据下列条件,判断△ABC与△A'B'C'是否相似,并说明理由.
AB=4 cm,BC=6 cm,AC=8 cm,A'B'=12 cm,B'C'=18 cm,A'C'=24 cm.
解:∵
∴
∴
△ABC ∽ △A'B'C'.
例2:要制作两个形状相同的三角形框架,其中一个三角形框架的三边长分别
为4、5、6,另一个三角形框架的一边长为2,它的另外两条边长应当是
多少?你有几种制作方案?
方案(1)
解:设另外两条边长分别为x , y
方案(2)
方案(3)
新知探究
新知探究
1、在△ABC和△DEF中,如果AB=4,BC=3,AC=6;DE=2.4,EF=1.2,FD=1.6,那么这两个三角形能否相似的结论是______,理由是__________________.
2、如图所示,小正方形的边长均为1,则下列选项中阴影部分的三角形与△ABC相似的( )
相似
A
三组对应边的比相等
课堂小结
相似三角形判定定理1
判定定理:如果两个三角形的三组对应边的比相等,那么这两个三角形相似.
简单地说:三边成比例的两个三角形相似.
课堂小测
1.在△ABC中,BC=15 cm,CA=45 cm,AB=63 cm,另一个和它相似的三角形
的最短边长是5 cm,则最长边长是 ( )
A.18 cm B.21 cm C.24 cm D.19.5 cm
B
2.如图所示,与左图中的三角形相似的是 ( )
A B C D
B
3.如果三角形的每条边都扩大为原来的3倍,那么三角形的每个角 ( )
A.都扩大为原来的3倍 B.都扩大为原来的6倍
C.都扩大为原来的9倍 D.都与原来相等
D
课堂小测
课堂小测
第二十七章
27.2相似三角形
九年级数学人教版·下册
27.2.1.2相似三角形的判定定理1
授课人:XXXX
教学目标
1.能运用三边成比例、两边成比例且夹角相等的两个三角形相似判定定理证明三角形相似;(重点)
2.三角形相似判定定理的证明过程.(难点)
新课导入
1、两个三角形全等有哪些判定方法?
2、我们学过哪些判定三角形相似的方法?
3、全等三角形与相似三角形有怎样的关系?
SSS、SAS、ASA、AAS、HL(直角三角形)
(1)定义;(2)对应角相等,对应边的比相等.
全等三角形一定是相似三角形,相似三角形不一定是全等三角形.
新知探究
任意画一个三角形,再画一个三角形,使它的各边长都是原来三角形各边长的k倍,度量这两个三角形的对应角,它们相等吗?这两个三角形相似吗?与同桌交流一下,看看是否有同样的结论.
是否有△ABC∽△A′B′C′?
A
B
C
C′
B′
A′
三边对应成 比例
新知探究
A
B
C
D
E
∴
又
∴
同理
∥
∴
在△ABC和△A′B′C′中,
求证:△ABC∽△A′B′C′.
△ABC∽△A′B′C′.
∴△ABC∽△A′B′C′.
∴△A′DE≌△ABC.
新知探究
A
B
C
判定定理:如果两个三角形的三组对应边的比相等,那么这两个三角形相似.
简单地说:三边成比例的两个三角形相似.
△ABC∽△A′B′C′.
新知探究
例1:根据下列条件,判断△ABC与△A'B'C'是否相似,并说明理由.
AB=4 cm,BC=6 cm,AC=8 cm,A'B'=12 cm,B'C'=18 cm,A'C'=24 cm.
解:∵
∴
∴
△ABC ∽ △A'B'C'.
例2:要制作两个形状相同的三角形框架,其中一个三角形框架的三边长分别
为4、5、6,另一个三角形框架的一边长为2,它的另外两条边长应当是
多少?你有几种制作方案?
方案(1)
解:设另外两条边长分别为x , y
方案(2)
方案(3)
新知探究
新知探究
1、在△ABC和△DEF中,如果AB=4,BC=3,AC=6;DE=2.4,EF=1.2,FD=1.6,那么这两个三角形能否相似的结论是______,理由是__________________.
2、如图所示,小正方形的边长均为1,则下列选项中阴影部分的三角形与△ABC相似的( )
相似
A
三组对应边的比相等
课堂小结
相似三角形判定定理1
判定定理:如果两个三角形的三组对应边的比相等,那么这两个三角形相似.
简单地说:三边成比例的两个三角形相似.
课堂小测
1.在△ABC中,BC=15 cm,CA=45 cm,AB=63 cm,另一个和它相似的三角形
的最短边长是5 cm,则最长边长是 ( )
A.18 cm B.21 cm C.24 cm D.19.5 cm
B
2.如图所示,与左图中的三角形相似的是 ( )
A B C D
B
3.如果三角形的每条边都扩大为原来的3倍,那么三角形的每个角 ( )
A.都扩大为原来的3倍 B.都扩大为原来的6倍
C.都扩大为原来的9倍 D.都与原来相等
D
课堂小测
课堂小测
