2021-2022学年度人教版九年级数学下册课件 27.2.1.3相似三角形的判定 (共13张PPT)
文档属性
| 名称 | 2021-2022学年度人教版九年级数学下册课件 27.2.1.3相似三角形的判定 (共13张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-19 17:56:16 | ||
图片预览





文档简介
(共13张PPT)
第二十七章
27.2相似三角形
九年级数学人教版·下册
27.2.1.3相似三角形的判定定理2
授课人:XXXX
教学目标
1.能运用两边成比例且夹角相等的两个三角形相似判定定理证明三角形相似;(重点)
2.三角形相似判定定理的证明过程.(难点)
新课导入
1、两个三角形全等有哪些判定方法?
2、我们学过哪些判定三角形相似的方法?
3、全等三角形与相似三角形有怎样的关系?
SSS、SAS、ASA、AAS、HL(直角三角形)
(1)定义;(2)对应角相等,对应边的比相等.
全等三角形一定是相似三角形,相似三角形不一定是全等三角形.
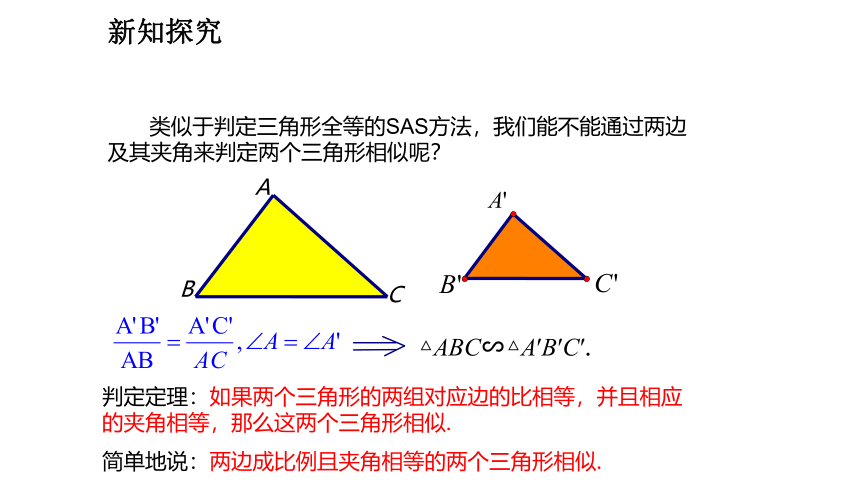
类似于判定三角形全等的SAS方法,我们能不能通过两边及其夹角来判定两个三角形相似呢?
A
B
C
判定定理:如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似.
简单地说:两边成比例且夹角相等的两个三角形相似.
新知探究
△ABC∽△A′B′C′.
新知探究
如图,在△ABC与△A′B′C′中,已知∠A= ∠A′,
证明:在△A′B′C′的边A′B′上截取点D,使
A′D=AB.过点D作DE∥B′C′,交A′C′于点E.
∵DE∥B′C′,
∴△A′DE∽△A′B′C′.
求证:△A′B′C′∽△ABC.
B
A
C
B'
A'
D
E
C'
∵A′D=AB,
∴A′E=AC. 又∠A′=∠A.
∴△A′DE≌△ABC, ∴△A′B′C′∽△ABC.
例1:在△ABC和△DEF中,∠C=∠F=70°,AC=3.5cm,BC=2.5 cm,DF=2.1 cm,EF=1.5 cm.求证:△DEF∽△ABC.
A
F
E
C
B
D
证明:∵AC=3.5cm,BC=2.5cm,DF=2.1cm,EF=1.5cm,
又∵∠C=∠F=70°,
∴ △DEF∽△ABC(两边成比例且夹角相等的两个三角形相似).
新知探究
例2: 如图,在 △ABC 中,CD是边AB上的高,且 . 求证:∠ACB=90°.
A
B
C
D
解: ∵ CD是边AB上的高,
∴ ∠ADC= ∠CDB=90°.
∴ △ADC∽△CDB,
∴ ∠ACD= ∠B,
∴ ∠ACB= ∠ACD+ ∠BCD= ∠B+ ∠BCD= 90°.
新知探究
∵
课堂小结
相似三角形的判定定理2
如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似.
简单地说:两边成比例且夹角相等的两个三角形相似.
课堂小测
1.如图所示,四边形ABCD的对角线AC,BD相交于O,且将这个四边形分成①②③④
四个三角形,若OA∶OC=OB∶OD,则下列结论中一定正确的是 ( )
A.①与②相似 B.①与③相似
C.①与④相似 D.②与④相似
B
2.已知线段AB,CD相交于O,AO=3,OB=6,CO=2,则当CD= 时,AC∥BD.
6
3.如图所示,△ABC中,点P在边AB上,在下列四个条件中:
①AP∶AC=AC∶AB;②AC2=AP·AB;③AB·CP=AP·CB.
能满足△APC和△ACB相似的有 个.
2
课堂小测
4.如图所示,D是∠ABC平分线上的一点,AB=15 cm,BD=12 cm,
要使△ABD∽△DBC,则BC的长为 cm.
9.6
课堂小测
解:∵AE=1.5,AC=2,
∴
∵ ∴
又∵∠EAD=∠CAB,
∴△ADE∽△ABC,
∴ ∵BC=3 , ∴DE=
5.如图所示,D,E分别是△ABC的边AC,AB上的点,
AE=1.5,AC=2,BC=3,且 ,求DE的长.
A
C
B
E
D
6.如图所示,点C,D在线段AB上,且△PCD是等边三角形.
(1)当AC,CD,DB满足怎样的关系时,△ACP∽△PDB
(2)当△ACP∽△PDB时,求∠APB的度数.
课堂小测
解:(1)∵△PCD是等边三角形,
∴PC=CD=PD,∠PCD=∠PDC=∠CPD=60°,
∴∠PCA=∠PDB=120°,
∴当CD2=AC·DB时,△ACP∽△PDB.
(2)∵△PDB∽△ACP,∴∠BPD=∠A.
∴∠APC+∠BPD=∠APC+∠A=∠PCD=60°,
∴∠APB=∠APC+∠BPD+∠CPD=60°+60°=120°.
第二十七章
27.2相似三角形
九年级数学人教版·下册
27.2.1.3相似三角形的判定定理2
授课人:XXXX
教学目标
1.能运用两边成比例且夹角相等的两个三角形相似判定定理证明三角形相似;(重点)
2.三角形相似判定定理的证明过程.(难点)
新课导入
1、两个三角形全等有哪些判定方法?
2、我们学过哪些判定三角形相似的方法?
3、全等三角形与相似三角形有怎样的关系?
SSS、SAS、ASA、AAS、HL(直角三角形)
(1)定义;(2)对应角相等,对应边的比相等.
全等三角形一定是相似三角形,相似三角形不一定是全等三角形.
类似于判定三角形全等的SAS方法,我们能不能通过两边及其夹角来判定两个三角形相似呢?
A
B
C
判定定理:如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似.
简单地说:两边成比例且夹角相等的两个三角形相似.
新知探究
△ABC∽△A′B′C′.
新知探究
如图,在△ABC与△A′B′C′中,已知∠A= ∠A′,
证明:在△A′B′C′的边A′B′上截取点D,使
A′D=AB.过点D作DE∥B′C′,交A′C′于点E.
∵DE∥B′C′,
∴△A′DE∽△A′B′C′.
求证:△A′B′C′∽△ABC.
B
A
C
B'
A'
D
E
C'
∵A′D=AB,
∴A′E=AC. 又∠A′=∠A.
∴△A′DE≌△ABC, ∴△A′B′C′∽△ABC.
例1:在△ABC和△DEF中,∠C=∠F=70°,AC=3.5cm,BC=2.5 cm,DF=2.1 cm,EF=1.5 cm.求证:△DEF∽△ABC.
A
F
E
C
B
D
证明:∵AC=3.5cm,BC=2.5cm,DF=2.1cm,EF=1.5cm,
又∵∠C=∠F=70°,
∴ △DEF∽△ABC(两边成比例且夹角相等的两个三角形相似).
新知探究
例2: 如图,在 △ABC 中,CD是边AB上的高,且 . 求证:∠ACB=90°.
A
B
C
D
解: ∵ CD是边AB上的高,
∴ ∠ADC= ∠CDB=90°.
∴ △ADC∽△CDB,
∴ ∠ACD= ∠B,
∴ ∠ACB= ∠ACD+ ∠BCD= ∠B+ ∠BCD= 90°.
新知探究
∵
课堂小结
相似三角形的判定定理2
如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似.
简单地说:两边成比例且夹角相等的两个三角形相似.
课堂小测
1.如图所示,四边形ABCD的对角线AC,BD相交于O,且将这个四边形分成①②③④
四个三角形,若OA∶OC=OB∶OD,则下列结论中一定正确的是 ( )
A.①与②相似 B.①与③相似
C.①与④相似 D.②与④相似
B
2.已知线段AB,CD相交于O,AO=3,OB=6,CO=2,则当CD= 时,AC∥BD.
6
3.如图所示,△ABC中,点P在边AB上,在下列四个条件中:
①AP∶AC=AC∶AB;②AC2=AP·AB;③AB·CP=AP·CB.
能满足△APC和△ACB相似的有 个.
2
课堂小测
4.如图所示,D是∠ABC平分线上的一点,AB=15 cm,BD=12 cm,
要使△ABD∽△DBC,则BC的长为 cm.
9.6
课堂小测
解:∵AE=1.5,AC=2,
∴
∵ ∴
又∵∠EAD=∠CAB,
∴△ADE∽△ABC,
∴ ∵BC=3 , ∴DE=
5.如图所示,D,E分别是△ABC的边AC,AB上的点,
AE=1.5,AC=2,BC=3,且 ,求DE的长.
A
C
B
E
D
6.如图所示,点C,D在线段AB上,且△PCD是等边三角形.
(1)当AC,CD,DB满足怎样的关系时,△ACP∽△PDB
(2)当△ACP∽△PDB时,求∠APB的度数.
课堂小测
解:(1)∵△PCD是等边三角形,
∴PC=CD=PD,∠PCD=∠PDC=∠CPD=60°,
∴∠PCA=∠PDB=120°,
∴当CD2=AC·DB时,△ACP∽△PDB.
(2)∵△PDB∽△ACP,∴∠BPD=∠A.
∴∠APC+∠BPD=∠APC+∠A=∠PCD=60°,
∴∠APB=∠APC+∠BPD+∠CPD=60°+60°=120°.
