2021-2022学年度人教版九年级数学 下册课件 27.2.1.4相似三角形的判定 (共17张PPT)
文档属性
| 名称 | 2021-2022学年度人教版九年级数学 下册课件 27.2.1.4相似三角形的判定 (共17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-19 17:59:06 | ||
图片预览





文档简介
(共17张PPT)
第二十七章
27.2相似三角形
九年级数学人教版·下册
27.2.1.4相似三角形的判定定理3
授课人:XXXX
教学目标
1.运用两角对应相等的两个三角形相似的判定定理证明三角形相似;(重点)
2.三角形相似判定定理的证明过程.(难点)
新课导入
相似三角形的识别方法有那些?
方法1:通过定义
方法3:两边对应成比例且夹角.
方法2:平行于三角形一边的直线.
新知探究
这两个三角形的三个内角的大小有什么关系?
三个内角对应相等的两个三角形一定相似吗?
三个内角对应相等.
观察你与老师的直角三角尺(30°与60°),会相似吗?
相
似
新知探究
画三角形,使三个角分别为60°,45°, 75° .
①分别量出两个三角形三边的长度;
②这两个三角形相似吗
即:如果一个三角形的三个角分别与另一个三角形的三个角对应相等,那么这两个三角形_______.
一定需三个角吗?
如果一个三角形的两角分别与另一个三角形的两角对应相等,那么这两个三角形相似.
相似三角形的识别方法:
思 考
如果两个三角形仅有一对角是对应相等的,那么它们是否一定相似?
相似
不一定
A
A'
B
B'
C'
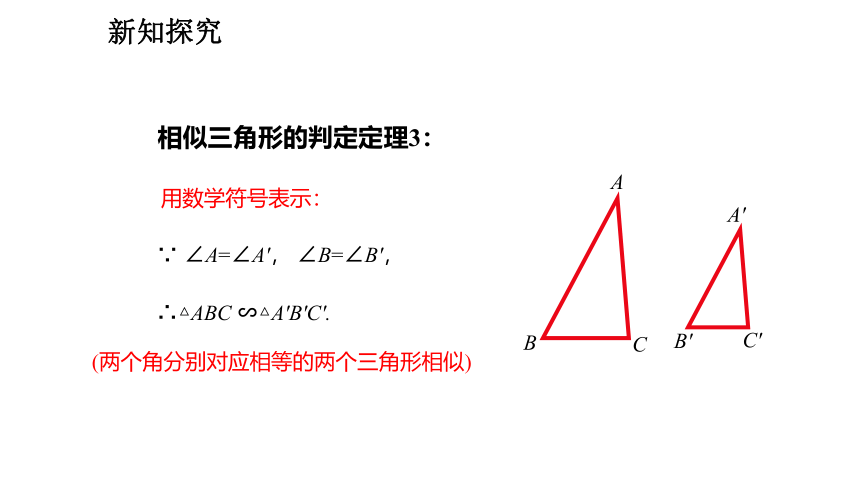
∵ ∠A=∠A', ∠B=∠B',
∴△ABC ∽△A'B'C'.
用数学符号表示:
相似三角形的判定定理3:
(两个角分别对应相等的两个三角形相似)
C
新知探究
新知探究
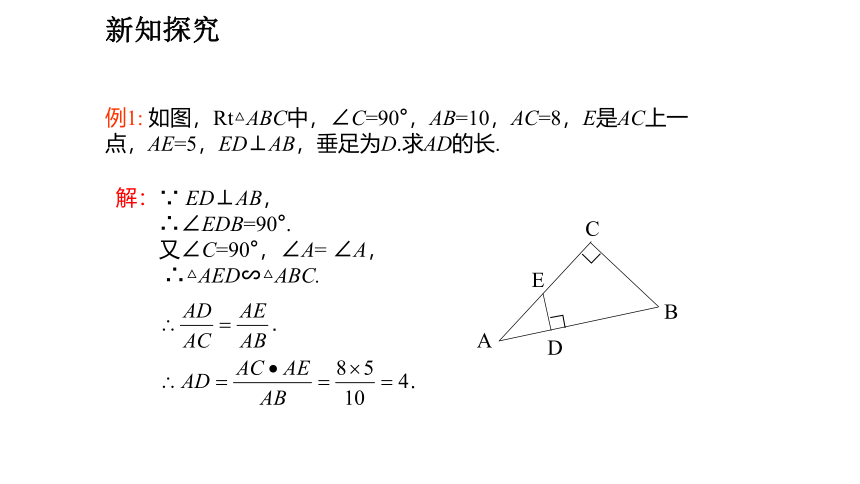
例1: 如图,Rt△ABC中,∠C=90°,AB=10,AC=8,E是AC上一点,AE=5,ED⊥AB,垂足为D.求AD的长.
A
B
C
D
E
∟
∟
解:∵ ED⊥AB,
∴∠EDB=90°.
又∠C=90°,∠A= ∠A,
∴△AED∽△ABC.
.
.
新知探究
已知: 在Rt△ABC和Rt△A'B'C'中,∠C=90°,∠C′=90°,
求证: Rt△ABC∽Rt△A'B'C'.
证明:设 = k,
由勾股定理,得 .
∴ .
∴ .
∴Rt △ABC∽Rt △A′B′C′.
思考 对于两个直角三角形,我们还可以用“HL”判定它们全等,那么,满足斜
边的比等于一组直角边的比的两个直角三角形相似吗?
如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例, 那么这两个直角三角形相似.
判定三角形相似的定理
A
B
C
∴△ABC∽△A1B1C1.
A1
B1
C1
在Rt△ABC 和 Rt△A1B1C1中,
符号语言:
新知探究
例2:如图所示,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,图中共有哪几对相似三
角形 请选择其中一对进行证明.
解:(1)△ACD∽△ABC,△CDB∽△ACB,△ACD∽△CBD.
(2)答案不唯一.
证明△ACD∽△ABC如下:
∵∠A+∠B=90°,∠A+∠ACD=90°,
∴∠B=∠ACD,
又∵∠ACB=∠ADC=90°,
∴△ACD∽△ABC.
新知探究
1、如图,D为△ABC的边AB上一点,且AB=4.AD=3,
∠ABC=∠ACD,则AC长为_____.
2、如图,△ABC中, DE∥BC,EF∥AB,
试说明△ADE∽△EFC.
解:∵ DE∥BC,
∴ ∠ADE= ∠B, ∠AED= ∠C.
∵ EF∥AB,
∴ ∠EFC= ∠B,则∠ADE= ∠EFC.
在△ADE 和△EFC 中,
∠AED= ∠C,
∠ADE= ∠EFC,
∴ △ADE∽△EFC.
新知探究
课堂小结
相似三角形判定定理3
判定定理:两个角分别对应相等的两个三角形相似.
判定定理: 如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例, 那么这两个直角三角形相似.
课堂小测
1、判断题:
⑴所有的直角三角形都相似.( )
⑵所有的等边三角形都相似.( )
⑶所有的等腰直角三角形都相似.( )
⑷有一个角相等的两等腰三角形相似.( )
×
√
√
×
课堂小测
2、已知:如图,△ABC与△ADE中,D在BC上,∠1=∠2=∠3.
求证:△ABC∽△ADE.
证明:∵△ABC与△ADE中,D在BC上,∠2=∠3,
∴∠E=∠C,
∵∠DAE=∠DAC+∠2,∠BAC=∠DAC+∠1,
且∠1=∠2,
∴∠DAE=∠BAC,
∵∠1=∠3,∠DAC=∠1+∠B=∠3+∠ADE,
∴∠B=∠ADE,
∴△ABC∽△ADE.
课堂小测
证明: ∵ △ABC 的高AD、BE交于点F
∴ ∠FEA=∠FDB=90°,∠AFE =∠BFD(对顶角相等)
在△ FDB和△FEA中 ∠FEA=∠FDB,
∠AFE =∠BFD,
∴ △FEA ∽ △ FDB,
∴ .
3、已知:如图,△ABC 的高AD、BE交于点F.
求证: .
课堂小测
4.△ABC为锐角三角形,BD、CE为高 .
求证:△ ADE∽ △ ABC.
证明:∵BD⊥AC,CE⊥AB,
∴∠ABD+∠A=90°,
∠ACE+∠A= 90°.
∴ ∠ABD= ∠ACE.
又∵ ∠A= ∠A,
∴△ ABD ∽ △ ACE.
∴
∵ ∠A= ∠A,
∴ △ ADE ∽ △ ABC.
A
B
D
C
E
O
第二十七章
27.2相似三角形
九年级数学人教版·下册
27.2.1.4相似三角形的判定定理3
授课人:XXXX
教学目标
1.运用两角对应相等的两个三角形相似的判定定理证明三角形相似;(重点)
2.三角形相似判定定理的证明过程.(难点)
新课导入
相似三角形的识别方法有那些?
方法1:通过定义
方法3:两边对应成比例且夹角.
方法2:平行于三角形一边的直线.
新知探究
这两个三角形的三个内角的大小有什么关系?
三个内角对应相等的两个三角形一定相似吗?
三个内角对应相等.
观察你与老师的直角三角尺(30°与60°),会相似吗?
相
似
新知探究
画三角形,使三个角分别为60°,45°, 75° .
①分别量出两个三角形三边的长度;
②这两个三角形相似吗
即:如果一个三角形的三个角分别与另一个三角形的三个角对应相等,那么这两个三角形_______.
一定需三个角吗?
如果一个三角形的两角分别与另一个三角形的两角对应相等,那么这两个三角形相似.
相似三角形的识别方法:
思 考
如果两个三角形仅有一对角是对应相等的,那么它们是否一定相似?
相似
不一定
A
A'
B
B'
C'
∵ ∠A=∠A', ∠B=∠B',
∴△ABC ∽△A'B'C'.
用数学符号表示:
相似三角形的判定定理3:
(两个角分别对应相等的两个三角形相似)
C
新知探究
新知探究
例1: 如图,Rt△ABC中,∠C=90°,AB=10,AC=8,E是AC上一点,AE=5,ED⊥AB,垂足为D.求AD的长.
A
B
C
D
E
∟
∟
解:∵ ED⊥AB,
∴∠EDB=90°.
又∠C=90°,∠A= ∠A,
∴△AED∽△ABC.
.
.
新知探究
已知: 在Rt△ABC和Rt△A'B'C'中,∠C=90°,∠C′=90°,
求证: Rt△ABC∽Rt△A'B'C'.
证明:设 = k,
由勾股定理,得 .
∴ .
∴ .
∴Rt △ABC∽Rt △A′B′C′.
思考 对于两个直角三角形,我们还可以用“HL”判定它们全等,那么,满足斜
边的比等于一组直角边的比的两个直角三角形相似吗?
如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例, 那么这两个直角三角形相似.
判定三角形相似的定理
A
B
C
∴△ABC∽△A1B1C1.
A1
B1
C1
在Rt△ABC 和 Rt△A1B1C1中,
符号语言:
新知探究
例2:如图所示,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,图中共有哪几对相似三
角形 请选择其中一对进行证明.
解:(1)△ACD∽△ABC,△CDB∽△ACB,△ACD∽△CBD.
(2)答案不唯一.
证明△ACD∽△ABC如下:
∵∠A+∠B=90°,∠A+∠ACD=90°,
∴∠B=∠ACD,
又∵∠ACB=∠ADC=90°,
∴△ACD∽△ABC.
新知探究
1、如图,D为△ABC的边AB上一点,且AB=4.AD=3,
∠ABC=∠ACD,则AC长为_____.
2、如图,△ABC中, DE∥BC,EF∥AB,
试说明△ADE∽△EFC.
解:∵ DE∥BC,
∴ ∠ADE= ∠B, ∠AED= ∠C.
∵ EF∥AB,
∴ ∠EFC= ∠B,则∠ADE= ∠EFC.
在△ADE 和△EFC 中,
∠AED= ∠C,
∠ADE= ∠EFC,
∴ △ADE∽△EFC.
新知探究
课堂小结
相似三角形判定定理3
判定定理:两个角分别对应相等的两个三角形相似.
判定定理: 如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例, 那么这两个直角三角形相似.
课堂小测
1、判断题:
⑴所有的直角三角形都相似.( )
⑵所有的等边三角形都相似.( )
⑶所有的等腰直角三角形都相似.( )
⑷有一个角相等的两等腰三角形相似.( )
×
√
√
×
课堂小测
2、已知:如图,△ABC与△ADE中,D在BC上,∠1=∠2=∠3.
求证:△ABC∽△ADE.
证明:∵△ABC与△ADE中,D在BC上,∠2=∠3,
∴∠E=∠C,
∵∠DAE=∠DAC+∠2,∠BAC=∠DAC+∠1,
且∠1=∠2,
∴∠DAE=∠BAC,
∵∠1=∠3,∠DAC=∠1+∠B=∠3+∠ADE,
∴∠B=∠ADE,
∴△ABC∽△ADE.
课堂小测
证明: ∵ △ABC 的高AD、BE交于点F
∴ ∠FEA=∠FDB=90°,∠AFE =∠BFD(对顶角相等)
在△ FDB和△FEA中 ∠FEA=∠FDB,
∠AFE =∠BFD,
∴ △FEA ∽ △ FDB,
∴ .
3、已知:如图,△ABC 的高AD、BE交于点F.
求证: .
课堂小测
4.△ABC为锐角三角形,BD、CE为高 .
求证:△ ADE∽ △ ABC.
证明:∵BD⊥AC,CE⊥AB,
∴∠ABD+∠A=90°,
∠ACE+∠A= 90°.
∴ ∠ABD= ∠ACE.
又∵ ∠A= ∠A,
∴△ ABD ∽ △ ACE.
∴
∵ ∠A= ∠A,
∴ △ ADE ∽ △ ABC.
A
B
D
C
E
O
