2021-2022学年度人教版九年级数学 下册课件 28.2.1解直角三角形 课件(共18张PPT)
文档属性
| 名称 | 2021-2022学年度人教版九年级数学 下册课件 28.2.1解直角三角形 课件(共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-19 19:49:30 | ||
图片预览




文档简介
(共18张PPT)
第二十八章
28.2解直角三角形及其应用
九年级数学人教版·下册
28.2.1解直角三角形
授课人:XXXX
教学目标
1.理解解直角三角形的概念;(重点)
2.理解并掌握解直角三角形的方法.(难点)
新课导入
A
C
B
c
b
a
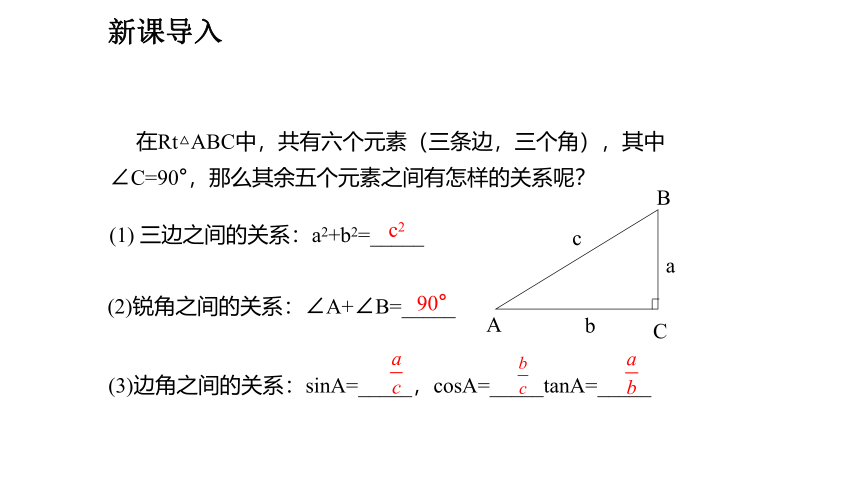
(1) 三边之间的关系:a2+b2=_____
(2)锐角之间的关系:∠A+∠B=_____
(3)边角之间的关系:sinA=_____,cosA=_____tanA=_____
在Rt△ABC中,共有六个元素(三条边,三个角),其中∠C=90°,那么其余五个元素之间有怎样的关系呢?
c2
90°
在本章引言中我们曾经描述过比萨斜塔倾斜程度的问题,把1972年的情形抽象为数学问题为:设塔顶中心点为B,塔身中心线与垂直中心线的夹角为∠A,过点B向垂直中心线引垂线,垂足为点C(如图所示).在Rt△ABC中,∠C=90°,BC=5.2 m,AB=54.5 m,求∠A的度数.
A
B
C
利用计算器可得∠A≈5°28′
在Rt△ABC中,你还能求出其他的边和角吗
已知直角三角形的斜边和一条直角边,求它的锐角的度数.
新课导入
新知探究
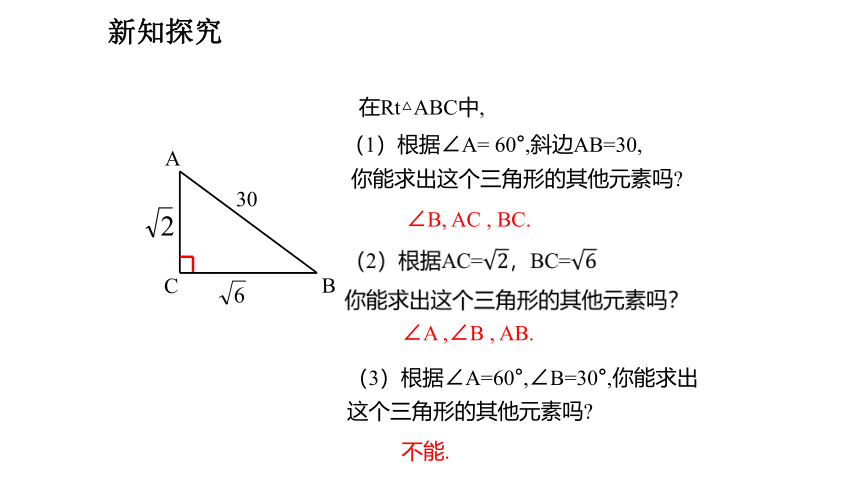
在Rt△ABC中,
(1)根据∠A= 60°,斜边AB=30,
A
B
C
∠B, AC , BC.
∠A ,∠B , AB.
(3)根据∠A=60°,∠B=30°,你能求出这个三角形的其他元素吗
不能.
你能求出这个三角形的其他元素吗
30
解直角三角形,只有两种:①已知两条边;②已知一条边和一个锐角.
定义:由直角三角形中的已知元素,求出其余未知元素的过程,叫做解直角三角形.
新知探究
新知探究
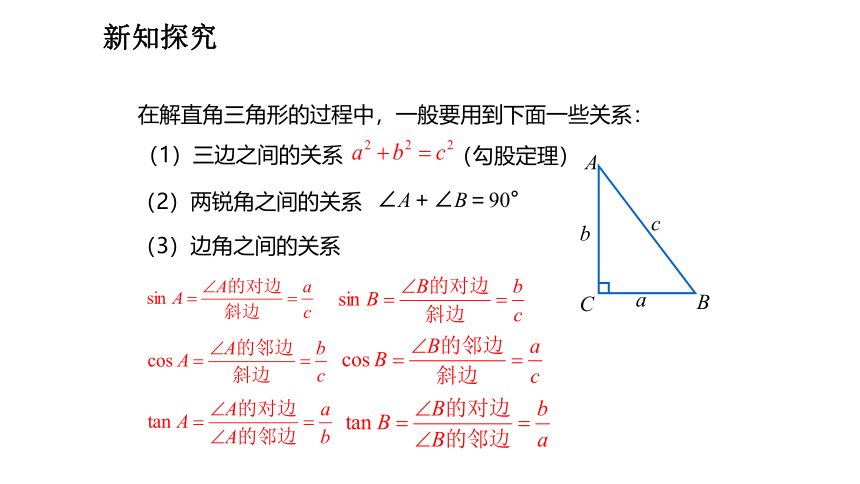
(2)两锐角之间的关系
∠A+∠B=90°
(3)边角之间的关系
(1)三边之间的关系
(勾股定理)
A
B
a
b
c
C
在解直角三角形的过程中,一般要用到下面一些关系:
图形 已知类型 已知条件 解法步骤
两边 斜边,一直角边(如c,a)
两直角边(a,b)
一边一角 斜边,一锐角(如c,∠A)
一直角边,一锐角(如a,∠A)
A
B
C
a
b
c
新知探究
解直角三角形的步骤:
新知探究
A
B
C
解:
新知探究
例2:如图所示,在Rt△ABC中, ∠C=90°, ∠B=35°,b=20,
解这个直角三角形(结果保留小数点后一位).
A
B
C
a
b
c
20
35°
(1)直角三角形中一共有六个元素,即三条边和三个角,除直角外,另外的五个元素中,只要已知一条边和一个角或两条边,就可以求出其余的所有未知元素.
(2)运用关系式解直角三角形时,常用到下列变形:①锐角之间的关系:∠A=90°-∠B,∠B=90°-∠A.②三边之间的常用变形: .
(3)边角之间的常用变形:a=c·sin A,b=c·cos A,a=b·tan A,a=c·cos B,b=c·sin B,b=a·tan B.
(4)虽然求未知元素时可选择的关系式有很多种,但为了计算方便,最好遵循“先求角后求边”和“宁乘不除”的原则.
(5)选择关系式时要尽量利用原始数据,以防“累积误差”.
(6)遇到不是直角三角形的图形时,要适当添加辅助线,将其转化为直角三角形求解.
新知探究
课堂小结
解直角三角形
解直角三角形的概念.
直角三角形中五个元素之间的关系.
解直角三角形的基本类型及解法步骤.
课堂小测
1.在下列直角三角形中不能求解的是( )
A.已知一直角边一锐角 B.已知一斜边一锐角
C.已知两边 D.已知两角
D
2.在△ABC中,a,b,c分别是∠A,∠B,∠C的对边,如果a2+b2=c2,
那么下列结论正确的是 ( )
A.csin A=a B.bcos B=c
C.atan A=b D.ctan B=b
A
课堂小测
C
A
课堂小测
45°
5
5
课堂小测
课堂小测
第二十八章
28.2解直角三角形及其应用
九年级数学人教版·下册
28.2.1解直角三角形
授课人:XXXX
教学目标
1.理解解直角三角形的概念;(重点)
2.理解并掌握解直角三角形的方法.(难点)
新课导入
A
C
B
c
b
a
(1) 三边之间的关系:a2+b2=_____
(2)锐角之间的关系:∠A+∠B=_____
(3)边角之间的关系:sinA=_____,cosA=_____tanA=_____
在Rt△ABC中,共有六个元素(三条边,三个角),其中∠C=90°,那么其余五个元素之间有怎样的关系呢?
c2
90°
在本章引言中我们曾经描述过比萨斜塔倾斜程度的问题,把1972年的情形抽象为数学问题为:设塔顶中心点为B,塔身中心线与垂直中心线的夹角为∠A,过点B向垂直中心线引垂线,垂足为点C(如图所示).在Rt△ABC中,∠C=90°,BC=5.2 m,AB=54.5 m,求∠A的度数.
A
B
C
利用计算器可得∠A≈5°28′
在Rt△ABC中,你还能求出其他的边和角吗
已知直角三角形的斜边和一条直角边,求它的锐角的度数.
新课导入
新知探究
在Rt△ABC中,
(1)根据∠A= 60°,斜边AB=30,
A
B
C
∠B, AC , BC.
∠A ,∠B , AB.
(3)根据∠A=60°,∠B=30°,你能求出这个三角形的其他元素吗
不能.
你能求出这个三角形的其他元素吗
30
解直角三角形,只有两种:①已知两条边;②已知一条边和一个锐角.
定义:由直角三角形中的已知元素,求出其余未知元素的过程,叫做解直角三角形.
新知探究
新知探究
(2)两锐角之间的关系
∠A+∠B=90°
(3)边角之间的关系
(1)三边之间的关系
(勾股定理)
A
B
a
b
c
C
在解直角三角形的过程中,一般要用到下面一些关系:
图形 已知类型 已知条件 解法步骤
两边 斜边,一直角边(如c,a)
两直角边(a,b)
一边一角 斜边,一锐角(如c,∠A)
一直角边,一锐角(如a,∠A)
A
B
C
a
b
c
新知探究
解直角三角形的步骤:
新知探究
A
B
C
解:
新知探究
例2:如图所示,在Rt△ABC中, ∠C=90°, ∠B=35°,b=20,
解这个直角三角形(结果保留小数点后一位).
A
B
C
a
b
c
20
35°
(1)直角三角形中一共有六个元素,即三条边和三个角,除直角外,另外的五个元素中,只要已知一条边和一个角或两条边,就可以求出其余的所有未知元素.
(2)运用关系式解直角三角形时,常用到下列变形:①锐角之间的关系:∠A=90°-∠B,∠B=90°-∠A.②三边之间的常用变形: .
(3)边角之间的常用变形:a=c·sin A,b=c·cos A,a=b·tan A,a=c·cos B,b=c·sin B,b=a·tan B.
(4)虽然求未知元素时可选择的关系式有很多种,但为了计算方便,最好遵循“先求角后求边”和“宁乘不除”的原则.
(5)选择关系式时要尽量利用原始数据,以防“累积误差”.
(6)遇到不是直角三角形的图形时,要适当添加辅助线,将其转化为直角三角形求解.
新知探究
课堂小结
解直角三角形
解直角三角形的概念.
直角三角形中五个元素之间的关系.
解直角三角形的基本类型及解法步骤.
课堂小测
1.在下列直角三角形中不能求解的是( )
A.已知一直角边一锐角 B.已知一斜边一锐角
C.已知两边 D.已知两角
D
2.在△ABC中,a,b,c分别是∠A,∠B,∠C的对边,如果a2+b2=c2,
那么下列结论正确的是 ( )
A.csin A=a B.bcos B=c
C.atan A=b D.ctan B=b
A
课堂小测
C
A
课堂小测
45°
5
5
课堂小测
课堂小测
