精讲精练·专项突破 第六章《平面向量及其应用》单元能力提升(含详细解析) (18)
文档属性
| 名称 | 精讲精练·专项突破 第六章《平面向量及其应用》单元能力提升(含详细解析) (18) |  | |
| 格式 | docx | ||
| 文件大小 | 110.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-18 16:27:25 | ||
图片预览




文档简介
精讲精练·专项突破
2021-2022学年高一下学期人教版(2019)
第六章 《平面向量及其应用》 单元能力提升(含详细解析)
一、单选题
1.(2021高一下·滨海新月考)下列说法中正确的是( )
A.若两个向量相等,则它们的起点和终点分别重合
B.模相等的两个平行向量是相等向量
C.若 和 都是单位向量,则
D.零向量与其它向量都共线
2.(2021高一下·抚顺期末)已知在 中,若 ,则 的值等于( )
A. B. C. D.
3.(2021高一下·长沙期末)已知 , 是单位向量,且 ,则( )
A. B.
C. =2 D. 与 的夹角为
4.(2021·陕西模拟)已知动点 在椭圆 上,若 点坐标为 , ,且 ,则 的最小值是( )
A. B. C.2 D.3
5.(2021高一下·肇庆期末)平面四边形 是边长为 的菱形,且 ,点 是 边上的点,且 ,点 是四边形 内或边界上的一个动点,则 的最大值为( )
A.1 B.3 C. D.4
6.(2021高二上·南阳期中)已知 的内角 , , 的对边分别为 , , ,若 , , ,则 外接圆半径为( )
A.2 B. C. D.1
7.(2021高一下·厦门期末)已知 , 是两个不共线的向量,且 , ,若 , , 三点共线,则实数 ( )
A.-4 B.-1 C.1 D.4
8.(2021高一下·隆阳期中)旅游区的玻璃栈道、玻璃桥、玻璃景观台等近年来热搜不断,因其惊险刺激的体验备受追捧.某景区顺应趋势,为扩大营收,准备在如图所示的山峰和山峰间建一座空中玻璃观景桥.已知两座山峰的高度都是,从点测得点的仰角,点的仰角以及,则两座山峰之间的距离( )
A. B. C. D.
二、多选题
9.(2021高一下·齐齐哈尔期中)定义平面向量之间的一种运算“ ”如下:对任意的 , ,令 ,下面说法正确的是( )
A.若 与 共线,则
B.
C.对任意的 ,有
D.
10.(2021高一下·辽宁期中)给出下列命题,其中正确的选项有( )
A.非零向量,满足,则与的夹角为30°
B.中,是成立的充要条件
C.若,,,为锐角,则实数的取值范围是
D.已知单位向量,,且,则当取最小值时,
11.(2021高二上·肥城期中)已知点 在平面 内,平面 ,其中 是平面 的一个法向量,则下列各点在平面 内的是( )
A. B. C. D.
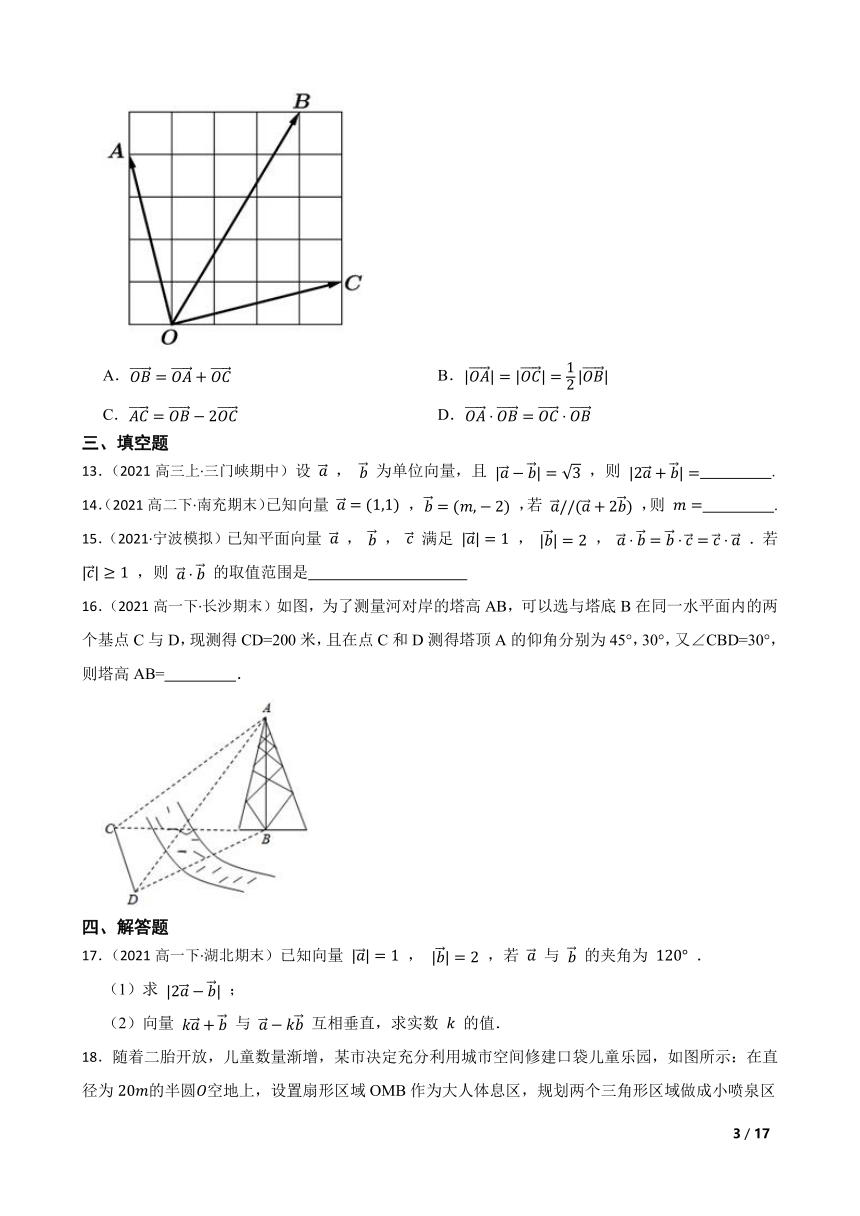
12.(2021高三上·苏州月考)如图所示,在4×4的方格中,点 , , , 均为小正方形的顶点,则下列结论正确的是( )
A. B.
C. D.
三、填空题
13.(2021高三上·三门峡期中)设 , 为单位向量,且 ,则 .
14.(2021高二下·南充期末)已知向量 , ,若 ,则 .
15.(2021·宁波模拟)已知平面向量 , , 满足 , , .若 ,则 的取值范围是
16.(2021高一下·长沙期末)如图,为了测量河对岸的塔高AB,可以选与塔底B在同一水平面内的两个基点C与D,现测得CD=200米,且在点C和D测得塔顶A的仰角分别为45°,30°,又∠CBD=30°,则塔高AB= .
四、解答题
17.(2021高一下·湖北期末)已知向量 , ,若 与 的夹角为 .
(1)求 ;
(2)向量 与 互相垂直,求实数 的值.
18.随着二胎开放,儿童数量渐增,某市决定充分利用城市空间修建口袋儿童乐园,如图所示:在直径为的半圆空地上,设置扇形区域OMB作为大人体息区,规划两个三角形区域做成小喷泉区(区域)和沙坑滑梯区(区域),其中为直径MN延长线上一点,且,为半圆周上一动点,以AB为边作等边.
(1)若等边的边长为,,试写出关于的函数关系式;
(2)问为多少时,儿童游玩区的面积最大?这个最大面积为多少?
19.(2021·淮安模拟)在 中,角 , , 所对的边分别是 , , ,已知 .
(1)求角 的大小;
(2)在下列三个条件中任选一个,补充在下面问题中的横线上,并解答.
若 , ,点 是 边上的一点,且 ▲ .求线段 的长.
① 是 的高;② 是 的中线;③ 是 的角平分线.
注:如果选择多个方案分别解答,按第一个方案解答计分.
20.(2021高一下·泰州期末)已知平面向量 , 满足 , ,其中 .
(1)若 ∥ ,求 ;
(2)若 ,求 与 夹角的余弦值.
21.(2022·益阳模拟)在①;②;③,这三个条作中任选一个,补充在下面的横线上,并解答.在中,角A,B,C所对的边分别为a,b,c,且____.
(1)求角C的大小;
(2)若,求AB的中线CD长度的最小值.
22.(2021高一下·德州期末)已知向量 ), ,其中 , ,且函数 周期为 .
(1)若 ,且 ,求 的值;
(2)方程 在 上有且仅有两个不同的实数解,求实数 的取值范围.
答案解析部分
1.【答案】D
【考点】零向量;单位向量;相等向量与相反向量
【解析】【解答】对于A选项,因为向量是可以移动的,两个向量相等时,它们的起点和终点不一定重合,A选项错误;
对于B选项,模相等的两个平行向量,可以是相等向量,也可以是相反向量,B选项错误;
对于C选项, 和 都是单位向量,但它们的方向不一定相同,故 和 不一定相等,C选项错误;
对于D选项,零向量的方向是任意的,零向量与其它向量都共线,D选项正确.
故答案为:D.
【分析】 根据平面向量的基本概念,对选项中的命题进行分析、判断正误即可.
2.【答案】D
【考点】正弦定理
【解析】【解答】解:因为 ,所以由正弦定理得 ,
所以 ,
故答案为:D
【分析】 直接利用正弦定理和三角函数的值的应用求出结果.
3.【答案】B
【考点】向量的模;单位向量;相等向量与相反向量;向量的线性运算性质及几何意义
【解析】【解答】解:∵
∴
如图,不妨设,则
则显然A错误;
则 ,故B正确;
则 =,故C错误;
则 与 的夹角为 ,故D错误
故答案为:B
【分析】根据向量的运算,结合单位向量,相等向量、向量的模、以及向量的夹角求解即可.
4.【答案】B
【考点】向量在几何中的应用
【解析】【解答】 点为椭圆的右焦点,由于 ,∴ .当 最小时, 最小,
的最小值为a-c=5-3=2,此时 .
故答案为:B
【分析】 根据推断出,进而利用勾股定理可知|PM|2=|AP|2-|AM|2,进而问题转化为求得|AP|最小值,但点A到椭圆的右顶点时|AP|最小,进而求得 的最小值 .
5.【答案】C
【考点】平面向量数量积的运算;向量的投影
【解析】【解答】如图,当 在 点时, 在 上的投影向量与 同向,且长度最长,
所以此时 最大,最大值为 ,
因为 ,
,所以
.
故答案为:C.
【分析】 根据数量积的几何意义, 在 上的投影向量与 同向且长度最长,有最大值,结合图形可得当M在C点时,最大,最大值为 。
6.【答案】D
【考点】两角和与差的正弦公式;二倍角的正弦公式;正弦定理
【解析】【解答】由正弦定理可得 ,即 ,又因为 ,
故 ,
结合两角和公式得 ,故 , ,由 。
故答案为:D
【分析】利用已知条件结合正弦定理得出 ,再利用 结合二倍角的正弦公式和三角形内角和为180度的性质,再结合诱导公式和两角和的正弦公式,从而求出角A的值,再结合正弦定理的性质,从而求出三角形 外接圆的半径。
7.【答案】A
【考点】平面向量的基本定理及其意义;三点共线
【解析】【解答】因为 , , 三点共线,所以 ,又因为 , ,则 ,即 ,因此 ,解得 。
故答案为:A.
【分析】利用已知条件结合平面向量基本定理和三点共线的判断方法,从而求出实数的值。
8.【答案】C
【考点】余弦定理的应用;解三角形的实际应用
【解析】【解答】由题意可知:,
, ,
由余弦定理得
故答案为:C
【分析】由勾股定理求出BM,再由余弦定理即可求MN.
9.【答案】A,C,D
【考点】平面向量数量积的运算
【解析】【解答】解:对于A,若 与 共线,则mq-np=0,即 ,所以A对;
对于B,由题意得 , ,所以 ,所以B错;
对于C,对于任意的λ∈R, ,所以 ,所以C对;
对于D, ,所以D对.
故答案为:ACD.
【分析】根据向量的数量积,结合对向量的新定义,直接求解即可.
10.【答案】A,B,D
【考点】平面向量数量积的坐标表示、模、夹角;正弦定理
【解析】【解答】解:对于A,如图,,则,
因为 ,则 为等边三角形,所以 , ,可得平行四边形 为菱形,所以 平分 ,即 ,所以 与 的夹角为30°,所以A正确;
对于B,由正弦定理得,当 时, ,反之当 时, ,所以 是 成立的充要条件,所以B正确;
对于C,因为 , , ,所以 , ,因为 为锐角,所以 且 不共线,由 ,得 ,解得 ,由 共线,得 ,得 ,所以当 为锐角时, 且 ,所以C错误;
对于D, ,所以当 时, 取最小值,所以D正确,
故答案为:ABD
【分析】由 ,通过平行四边形法即可判断A,由正弦定理即可判断B,由因为 为锐角,所以且不共线,列出不等式即可判断C.由即可求最小值,判断D
11.【答案】A,C
【考点】平面向量数量积的运算
【解析】【解答】设平面 内点的坐标为 ,
则 ,
平面 的一个法向量是 ,
所以 ,
即 .
故答案为:AC
【分析】设平面 内点的坐标为 ,利用,得到,即可得到答案.
12.【答案】A,D
【考点】平面向量的坐标运算;平面向量数量积的运算
【解析】【解答】由题意可知,以 为原点建立直角坐标系,
则各点坐标可写为: , , , ,
所以 , , , ,
,A符合题意;
, ,B不符合题意;
,
C不符合题意;
,D符合题意.
故答案为:AD.
【分析】 首先利用已知条件建立平面直角坐标系,进一步求出A、B、C的坐标,再利用向量的坐标运算和数量积运算逐项进行判断,可得答案.
13.【答案】
【考点】平面向量数量积的运算
【解析】【解答】因为 , 为单位向量,且 ,
所以 ,即 ,
所以 .
所以 .
故答案为: .
【分析】由已知结合向量数量积的性质可求得,进而求出 的值。
14.【答案】-2
【考点】平面向量的坐标运算;平面向量共线(平行)的坐标表示
【解析】【解答】因为 , ,所以 ,
又 ,所以 ,解得 .
故答案为: -2
【分析】根据题意求出向量的坐标,再由共线向量的坐标公式代入数值计算出结果即可。
15.【答案】
【考点】向量的模;数量积的坐标表达式
【解析】【解答】解:记 , , ,则 , , .
由题意 , ,可得 (显然 )
又由 ,得 ,消去n得 ,
化简得 ,即 .
结合 ,可解得 或 .
因此, .
故答案为:
【分析】首先由数量积的坐标公式整理即可得到,,,由此求解出再由向量模的定义结合已知条件即可得出不等式,求解出m的取值范围,由此即可得出的取值范围。
16.【答案】200m
【考点】余弦定理的应用
【解析】【解答】解:在△ABC中,∠ACB=45° , 在△ABD中,∠ADB=30° ,
设AB=x , 则BC=x, ,
在△BCD中,CD=200 , ∠CBD = 30°
由余弦定理得:CD2=BC2+BD2-2BC·BD·cos∠CBD
即
故答案为:200m
【分析】根据余弦定理直接求解即可.
17.【答案】(1)因为 , , 与 的夹角为 .
所以
所以
(2)因为向量 与 互相垂直,
所以 ,
所以
所以 ,
【考点】平面向量数量积的坐标表示、模、夹角;平面向量数量积的运算;数量积判断两个平面向量的垂直关系
【解析】【分析】(1)利用已知条件结合数量积的定义,从而结合数量积求向量的模的公式,进而求出向量的模。
(2)利用两向量垂直数量积为0的等价关系,再结合数量积的运算法则,从而利用数量积的定义,进而求出k的值。
18.【答案】(1)解:,,
在中,,,,,
由余弦定理可得,
所以,,其中;
(2)解:
,,
所以, ,
,则,
当时,即当时,四边形的面积取最大值.
【考点】三角函数的最值;余弦定理;三角形中的几何计算
【解析】【分析】(1)在 中 ,直接由余弦定理即可求出 关于的函数关系式 ;
(2)先求出 ,, 从而可得 , 由三角函数知识即可求最大值。
19.【答案】(1)因为 ,所以整理得 ,
所以由余弦定理得 ,
因为 ,所以
(2)选①, 是 的高
由余弦定理得 ,所以
所以根据等面积法 得 ;
选②, 是 的中线,
则由于 ,所以 ,
所以 ,
所以 ;
选③, 是 的角平分线
由于 ,
所以 ,即 ,
解得 .
【考点】余弦定理
【解析】【分析】(1)由题得 ,进而根据余弦定理可得 ;
(2)选 ① ,由余弦定理得 ,进而根据等面积法求解即可; 选② 根据 并结合向量的模的计算即可; 选③ ,根据 计算即可得答案。
20.【答案】(1)由 , ,解得 , .
因为 ∥ ,所以 ,解得 .
所以 , .
(2)当 时, , ,则 ,
, .
设 与 的夹角为 ,则 .
所以 与 夹角的余弦值为 .
【考点】向量的模;平面向量共线(平行)的坐标表示;平面向量数量积的坐标表示、模、夹角
【解析】【分析】 (1)根据已知条件,运用向量的平行公式,可得m=1,再结合向量模公式,即可求解;
(2)根据已知条件,结合向量的夹角公式,即可求解.
21.【答案】(1)解:选择条件①:由及正弦定理,得:,
即,由余弦定理,得,
因为,所以;
选择条件②:由及正弦定理,
得:,
即.
即.
在中,,所以,
即,因为,所以,所以,
因为,所以;
选择条件③:由及正弦定理,
得:,
因为,,所以.
在中,,则,
故.
因为,所以,则,
故;
(2)解:因为,所以,
整理得,
在三角形中,由余弦定理得.
因为,当且仅当时取等号,
所以,即,
所以,即,
即长度的最小值为.
【考点】解三角形;正弦定理;余弦定理
【解析】【分析】(1) 选择条件① 由正弦定理整理化简已知条件整理化简即可得出关于a、b、c的关系式,并把结果代入到余弦定理计算出cosC的取值,从而即可得出角C的大小。 选择条件② ,由正弦定理以及两角和的正弦公式整理化简已知条件,再由诱导公式整理化简由此计算出cosC的取值,从而求出角C的大小; 选择条件③ 首先由正弦定理整理化简已知条件,然后由两角和的正弦公式结合三角形的内角和的性质由此计算出sinC的取值,从而即可得出角C的取值。
(2)由已知条件结合余弦定理代入数值计算出 ,然后把结果代入到余弦定理结合基本不等式即可求出最小值。
22.【答案】(1)解:
因为 ,
所以 ,
所以
又因为
所以
所以 ;
(2)方程 在 上有且仅有两个不同的实数解等价于函数 与 在 有且仅有两个不同的交点,
时, , ,
所以 ,在 上为增函数,在 为减函数
, , ,
所以
所以 时,函数 与 在 有且仅有两个不同的交点,
即所求 的范围是 .
【考点】函数单调性的判断与证明;数量积的坐标表达式;三角函数的恒等变换及化简求值;三角函数的周期性及其求法;函数的零点与方程根的关系
【解析】【分析】(1)利用已知条件结合数量积的坐标表示结合二倍角的正弦公式和余弦公式,再利用辅助角公式化简函数为正弦型函数,再利用正弦型函数的最小正周期公式,从而求出的值,进而求出正弦型函数的解析式,再结合角的取值范围结合已知条件,再利用同角三角函数基本关系式,从而求出角的余弦值,再利用代入法结合两角和的正弦公式和角的正弦值和余弦值,从而求出 的值。
(2) 利用方程 在 上有且仅有两个不同的实数解等价于函数 与 在 有且仅有两个不同的交点,再利用x的取值范围结合已知条件,从而求出x的值,再利用的单调函数的定义,从而推出 在 上为增函数,在 为减函数,再利用函数 与直线 的图像,从而求出实数t的取值范围。
1 / 1
2021-2022学年高一下学期人教版(2019)
第六章 《平面向量及其应用》 单元能力提升(含详细解析)
一、单选题
1.(2021高一下·滨海新月考)下列说法中正确的是( )
A.若两个向量相等,则它们的起点和终点分别重合
B.模相等的两个平行向量是相等向量
C.若 和 都是单位向量,则
D.零向量与其它向量都共线
2.(2021高一下·抚顺期末)已知在 中,若 ,则 的值等于( )
A. B. C. D.
3.(2021高一下·长沙期末)已知 , 是单位向量,且 ,则( )
A. B.
C. =2 D. 与 的夹角为
4.(2021·陕西模拟)已知动点 在椭圆 上,若 点坐标为 , ,且 ,则 的最小值是( )
A. B. C.2 D.3
5.(2021高一下·肇庆期末)平面四边形 是边长为 的菱形,且 ,点 是 边上的点,且 ,点 是四边形 内或边界上的一个动点,则 的最大值为( )
A.1 B.3 C. D.4
6.(2021高二上·南阳期中)已知 的内角 , , 的对边分别为 , , ,若 , , ,则 外接圆半径为( )
A.2 B. C. D.1
7.(2021高一下·厦门期末)已知 , 是两个不共线的向量,且 , ,若 , , 三点共线,则实数 ( )
A.-4 B.-1 C.1 D.4
8.(2021高一下·隆阳期中)旅游区的玻璃栈道、玻璃桥、玻璃景观台等近年来热搜不断,因其惊险刺激的体验备受追捧.某景区顺应趋势,为扩大营收,准备在如图所示的山峰和山峰间建一座空中玻璃观景桥.已知两座山峰的高度都是,从点测得点的仰角,点的仰角以及,则两座山峰之间的距离( )
A. B. C. D.
二、多选题
9.(2021高一下·齐齐哈尔期中)定义平面向量之间的一种运算“ ”如下:对任意的 , ,令 ,下面说法正确的是( )
A.若 与 共线,则
B.
C.对任意的 ,有
D.
10.(2021高一下·辽宁期中)给出下列命题,其中正确的选项有( )
A.非零向量,满足,则与的夹角为30°
B.中,是成立的充要条件
C.若,,,为锐角,则实数的取值范围是
D.已知单位向量,,且,则当取最小值时,
11.(2021高二上·肥城期中)已知点 在平面 内,平面 ,其中 是平面 的一个法向量,则下列各点在平面 内的是( )
A. B. C. D.
12.(2021高三上·苏州月考)如图所示,在4×4的方格中,点 , , , 均为小正方形的顶点,则下列结论正确的是( )
A. B.
C. D.
三、填空题
13.(2021高三上·三门峡期中)设 , 为单位向量,且 ,则 .
14.(2021高二下·南充期末)已知向量 , ,若 ,则 .
15.(2021·宁波模拟)已知平面向量 , , 满足 , , .若 ,则 的取值范围是
16.(2021高一下·长沙期末)如图,为了测量河对岸的塔高AB,可以选与塔底B在同一水平面内的两个基点C与D,现测得CD=200米,且在点C和D测得塔顶A的仰角分别为45°,30°,又∠CBD=30°,则塔高AB= .
四、解答题
17.(2021高一下·湖北期末)已知向量 , ,若 与 的夹角为 .
(1)求 ;
(2)向量 与 互相垂直,求实数 的值.
18.随着二胎开放,儿童数量渐增,某市决定充分利用城市空间修建口袋儿童乐园,如图所示:在直径为的半圆空地上,设置扇形区域OMB作为大人体息区,规划两个三角形区域做成小喷泉区(区域)和沙坑滑梯区(区域),其中为直径MN延长线上一点,且,为半圆周上一动点,以AB为边作等边.
(1)若等边的边长为,,试写出关于的函数关系式;
(2)问为多少时,儿童游玩区的面积最大?这个最大面积为多少?
19.(2021·淮安模拟)在 中,角 , , 所对的边分别是 , , ,已知 .
(1)求角 的大小;
(2)在下列三个条件中任选一个,补充在下面问题中的横线上,并解答.
若 , ,点 是 边上的一点,且 ▲ .求线段 的长.
① 是 的高;② 是 的中线;③ 是 的角平分线.
注:如果选择多个方案分别解答,按第一个方案解答计分.
20.(2021高一下·泰州期末)已知平面向量 , 满足 , ,其中 .
(1)若 ∥ ,求 ;
(2)若 ,求 与 夹角的余弦值.
21.(2022·益阳模拟)在①;②;③,这三个条作中任选一个,补充在下面的横线上,并解答.在中,角A,B,C所对的边分别为a,b,c,且____.
(1)求角C的大小;
(2)若,求AB的中线CD长度的最小值.
22.(2021高一下·德州期末)已知向量 ), ,其中 , ,且函数 周期为 .
(1)若 ,且 ,求 的值;
(2)方程 在 上有且仅有两个不同的实数解,求实数 的取值范围.
答案解析部分
1.【答案】D
【考点】零向量;单位向量;相等向量与相反向量
【解析】【解答】对于A选项,因为向量是可以移动的,两个向量相等时,它们的起点和终点不一定重合,A选项错误;
对于B选项,模相等的两个平行向量,可以是相等向量,也可以是相反向量,B选项错误;
对于C选项, 和 都是单位向量,但它们的方向不一定相同,故 和 不一定相等,C选项错误;
对于D选项,零向量的方向是任意的,零向量与其它向量都共线,D选项正确.
故答案为:D.
【分析】 根据平面向量的基本概念,对选项中的命题进行分析、判断正误即可.
2.【答案】D
【考点】正弦定理
【解析】【解答】解:因为 ,所以由正弦定理得 ,
所以 ,
故答案为:D
【分析】 直接利用正弦定理和三角函数的值的应用求出结果.
3.【答案】B
【考点】向量的模;单位向量;相等向量与相反向量;向量的线性运算性质及几何意义
【解析】【解答】解:∵
∴
如图,不妨设,则
则显然A错误;
则 ,故B正确;
则 =,故C错误;
则 与 的夹角为 ,故D错误
故答案为:B
【分析】根据向量的运算,结合单位向量,相等向量、向量的模、以及向量的夹角求解即可.
4.【答案】B
【考点】向量在几何中的应用
【解析】【解答】 点为椭圆的右焦点,由于 ,∴ .当 最小时, 最小,
的最小值为a-c=5-3=2,此时 .
故答案为:B
【分析】 根据推断出,进而利用勾股定理可知|PM|2=|AP|2-|AM|2,进而问题转化为求得|AP|最小值,但点A到椭圆的右顶点时|AP|最小,进而求得 的最小值 .
5.【答案】C
【考点】平面向量数量积的运算;向量的投影
【解析】【解答】如图,当 在 点时, 在 上的投影向量与 同向,且长度最长,
所以此时 最大,最大值为 ,
因为 ,
,所以
.
故答案为:C.
【分析】 根据数量积的几何意义, 在 上的投影向量与 同向且长度最长,有最大值,结合图形可得当M在C点时,最大,最大值为 。
6.【答案】D
【考点】两角和与差的正弦公式;二倍角的正弦公式;正弦定理
【解析】【解答】由正弦定理可得 ,即 ,又因为 ,
故 ,
结合两角和公式得 ,故 , ,由 。
故答案为:D
【分析】利用已知条件结合正弦定理得出 ,再利用 结合二倍角的正弦公式和三角形内角和为180度的性质,再结合诱导公式和两角和的正弦公式,从而求出角A的值,再结合正弦定理的性质,从而求出三角形 外接圆的半径。
7.【答案】A
【考点】平面向量的基本定理及其意义;三点共线
【解析】【解答】因为 , , 三点共线,所以 ,又因为 , ,则 ,即 ,因此 ,解得 。
故答案为:A.
【分析】利用已知条件结合平面向量基本定理和三点共线的判断方法,从而求出实数的值。
8.【答案】C
【考点】余弦定理的应用;解三角形的实际应用
【解析】【解答】由题意可知:,
, ,
由余弦定理得
故答案为:C
【分析】由勾股定理求出BM,再由余弦定理即可求MN.
9.【答案】A,C,D
【考点】平面向量数量积的运算
【解析】【解答】解:对于A,若 与 共线,则mq-np=0,即 ,所以A对;
对于B,由题意得 , ,所以 ,所以B错;
对于C,对于任意的λ∈R, ,所以 ,所以C对;
对于D, ,所以D对.
故答案为:ACD.
【分析】根据向量的数量积,结合对向量的新定义,直接求解即可.
10.【答案】A,B,D
【考点】平面向量数量积的坐标表示、模、夹角;正弦定理
【解析】【解答】解:对于A,如图,,则,
因为 ,则 为等边三角形,所以 , ,可得平行四边形 为菱形,所以 平分 ,即 ,所以 与 的夹角为30°,所以A正确;
对于B,由正弦定理得,当 时, ,反之当 时, ,所以 是 成立的充要条件,所以B正确;
对于C,因为 , , ,所以 , ,因为 为锐角,所以 且 不共线,由 ,得 ,解得 ,由 共线,得 ,得 ,所以当 为锐角时, 且 ,所以C错误;
对于D, ,所以当 时, 取最小值,所以D正确,
故答案为:ABD
【分析】由 ,通过平行四边形法即可判断A,由正弦定理即可判断B,由因为 为锐角,所以且不共线,列出不等式即可判断C.由即可求最小值,判断D
11.【答案】A,C
【考点】平面向量数量积的运算
【解析】【解答】设平面 内点的坐标为 ,
则 ,
平面 的一个法向量是 ,
所以 ,
即 .
故答案为:AC
【分析】设平面 内点的坐标为 ,利用,得到,即可得到答案.
12.【答案】A,D
【考点】平面向量的坐标运算;平面向量数量积的运算
【解析】【解答】由题意可知,以 为原点建立直角坐标系,
则各点坐标可写为: , , , ,
所以 , , , ,
,A符合题意;
, ,B不符合题意;
,
C不符合题意;
,D符合题意.
故答案为:AD.
【分析】 首先利用已知条件建立平面直角坐标系,进一步求出A、B、C的坐标,再利用向量的坐标运算和数量积运算逐项进行判断,可得答案.
13.【答案】
【考点】平面向量数量积的运算
【解析】【解答】因为 , 为单位向量,且 ,
所以 ,即 ,
所以 .
所以 .
故答案为: .
【分析】由已知结合向量数量积的性质可求得,进而求出 的值。
14.【答案】-2
【考点】平面向量的坐标运算;平面向量共线(平行)的坐标表示
【解析】【解答】因为 , ,所以 ,
又 ,所以 ,解得 .
故答案为: -2
【分析】根据题意求出向量的坐标,再由共线向量的坐标公式代入数值计算出结果即可。
15.【答案】
【考点】向量的模;数量积的坐标表达式
【解析】【解答】解:记 , , ,则 , , .
由题意 , ,可得 (显然 )
又由 ,得 ,消去n得 ,
化简得 ,即 .
结合 ,可解得 或 .
因此, .
故答案为:
【分析】首先由数量积的坐标公式整理即可得到,,,由此求解出再由向量模的定义结合已知条件即可得出不等式,求解出m的取值范围,由此即可得出的取值范围。
16.【答案】200m
【考点】余弦定理的应用
【解析】【解答】解:在△ABC中,∠ACB=45° , 在△ABD中,∠ADB=30° ,
设AB=x , 则BC=x, ,
在△BCD中,CD=200 , ∠CBD = 30°
由余弦定理得:CD2=BC2+BD2-2BC·BD·cos∠CBD
即
故答案为:200m
【分析】根据余弦定理直接求解即可.
17.【答案】(1)因为 , , 与 的夹角为 .
所以
所以
(2)因为向量 与 互相垂直,
所以 ,
所以
所以 ,
【考点】平面向量数量积的坐标表示、模、夹角;平面向量数量积的运算;数量积判断两个平面向量的垂直关系
【解析】【分析】(1)利用已知条件结合数量积的定义,从而结合数量积求向量的模的公式,进而求出向量的模。
(2)利用两向量垂直数量积为0的等价关系,再结合数量积的运算法则,从而利用数量积的定义,进而求出k的值。
18.【答案】(1)解:,,
在中,,,,,
由余弦定理可得,
所以,,其中;
(2)解:
,,
所以, ,
,则,
当时,即当时,四边形的面积取最大值.
【考点】三角函数的最值;余弦定理;三角形中的几何计算
【解析】【分析】(1)在 中 ,直接由余弦定理即可求出 关于的函数关系式 ;
(2)先求出 ,, 从而可得 , 由三角函数知识即可求最大值。
19.【答案】(1)因为 ,所以整理得 ,
所以由余弦定理得 ,
因为 ,所以
(2)选①, 是 的高
由余弦定理得 ,所以
所以根据等面积法 得 ;
选②, 是 的中线,
则由于 ,所以 ,
所以 ,
所以 ;
选③, 是 的角平分线
由于 ,
所以 ,即 ,
解得 .
【考点】余弦定理
【解析】【分析】(1)由题得 ,进而根据余弦定理可得 ;
(2)选 ① ,由余弦定理得 ,进而根据等面积法求解即可; 选② 根据 并结合向量的模的计算即可; 选③ ,根据 计算即可得答案。
20.【答案】(1)由 , ,解得 , .
因为 ∥ ,所以 ,解得 .
所以 , .
(2)当 时, , ,则 ,
, .
设 与 的夹角为 ,则 .
所以 与 夹角的余弦值为 .
【考点】向量的模;平面向量共线(平行)的坐标表示;平面向量数量积的坐标表示、模、夹角
【解析】【分析】 (1)根据已知条件,运用向量的平行公式,可得m=1,再结合向量模公式,即可求解;
(2)根据已知条件,结合向量的夹角公式,即可求解.
21.【答案】(1)解:选择条件①:由及正弦定理,得:,
即,由余弦定理,得,
因为,所以;
选择条件②:由及正弦定理,
得:,
即.
即.
在中,,所以,
即,因为,所以,所以,
因为,所以;
选择条件③:由及正弦定理,
得:,
因为,,所以.
在中,,则,
故.
因为,所以,则,
故;
(2)解:因为,所以,
整理得,
在三角形中,由余弦定理得.
因为,当且仅当时取等号,
所以,即,
所以,即,
即长度的最小值为.
【考点】解三角形;正弦定理;余弦定理
【解析】【分析】(1) 选择条件① 由正弦定理整理化简已知条件整理化简即可得出关于a、b、c的关系式,并把结果代入到余弦定理计算出cosC的取值,从而即可得出角C的大小。 选择条件② ,由正弦定理以及两角和的正弦公式整理化简已知条件,再由诱导公式整理化简由此计算出cosC的取值,从而求出角C的大小; 选择条件③ 首先由正弦定理整理化简已知条件,然后由两角和的正弦公式结合三角形的内角和的性质由此计算出sinC的取值,从而即可得出角C的取值。
(2)由已知条件结合余弦定理代入数值计算出 ,然后把结果代入到余弦定理结合基本不等式即可求出最小值。
22.【答案】(1)解:
因为 ,
所以 ,
所以
又因为
所以
所以 ;
(2)方程 在 上有且仅有两个不同的实数解等价于函数 与 在 有且仅有两个不同的交点,
时, , ,
所以 ,在 上为增函数,在 为减函数
, , ,
所以
所以 时,函数 与 在 有且仅有两个不同的交点,
即所求 的范围是 .
【考点】函数单调性的判断与证明;数量积的坐标表达式;三角函数的恒等变换及化简求值;三角函数的周期性及其求法;函数的零点与方程根的关系
【解析】【分析】(1)利用已知条件结合数量积的坐标表示结合二倍角的正弦公式和余弦公式,再利用辅助角公式化简函数为正弦型函数,再利用正弦型函数的最小正周期公式,从而求出的值,进而求出正弦型函数的解析式,再结合角的取值范围结合已知条件,再利用同角三角函数基本关系式,从而求出角的余弦值,再利用代入法结合两角和的正弦公式和角的正弦值和余弦值,从而求出 的值。
(2) 利用方程 在 上有且仅有两个不同的实数解等价于函数 与 在 有且仅有两个不同的交点,再利用x的取值范围结合已知条件,从而求出x的值,再利用的单调函数的定义,从而推出 在 上为增函数,在 为减函数,再利用函数 与直线 的图像,从而求出实数t的取值范围。
1 / 1
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
