精讲精练·专项突破 第六章《平面向量及其应用》单元能力提升(含详细解析) (21)
文档属性
| 名称 | 精讲精练·专项突破 第六章《平面向量及其应用》单元能力提升(含详细解析) (21) |  | |
| 格式 | docx | ||
| 文件大小 | 199.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-18 16:27:35 | ||
图片预览




文档简介
精讲精练·专项突破
2021-2022学年高一下学期人教版(2019)
第六章 《平面向量及其应用》 单元能力提升(含详细解析)
一、单选题
1.(2020高二上·新余期末)在 中,若 , , ,则边 的长为( )
A. B. C. D.4
【答案】B
【考点】余弦定理
【解析】【解答】由题意可知: ,
故 或 ,
其中A=0不成立,则 ,
∵AB=2,AC=3,
∴由余弦定理得BC2=AB2+AC2 2AB×AC×cosA=19,
∴ .
故答案为:B.
【分析】 根据辅助角公式求出A的大小,利用余弦定理即可得到结论.
2.(2022·浙江模拟)已知非零向量,,则“”是“”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
【答案】A
【考点】必要条件、充分条件与充要条件的判断;平面向量共线(平行)的坐标表示
【解析】【解答】由,则,故,即充分性成立,
由 ,若 时必要性不成立.
所以“ ”是“ ”的充分不必要条件.
故答案为:A
【分析】根据充分、必要性的定义,结合向量平行的坐标表示判断条件间的推出关系,即可得答案.
3.(2020高二上·泸县期末)设 为坐标原点, , 是双曲线 的焦点,若双曲线上存在点 ,满足 , ,则该双曲线的离心率为( )
A. B. C. D.
【答案】B
【考点】双曲线的定义;双曲线的简单性质;余弦定理
【解析】【解答】由 ,可得 ,
在直角三角形 中, ,所以 ,
在△ 中,由余弦定理得:
,
所以 ,由双曲线定义可得 ,
解得离心率 .
故答案为:B.
【分析】 由题意作出图形,由已知可得OP⊥PF1,再由已知求得|,,然后结合双曲线定义计算出结果即可。
4.(2021高二下·南京开学考)如图,在三棱柱ABC-A1B1C1中,BC1与B1C相交于点O,∠A1AB=∠A1AC= ,∠BAC= ,A1A=3,AB=AC=2,则线段AO的长度为( )
A. B. C. D.
【答案】A
【考点】平面向量的基本定理及其意义;平面向量数量积的含义与物理意义;平面向量数量积的坐标表示、模、夹角;平面向量数量积的运算
【解析】【解答】因为四边形 是平行四边形,
,
,
,
,
,
,
,
即 。
故答案为:A
【分析】因为四边形 是平行四边形,再利用中点的性质结合平行四边形法则,得出
,再利用三角形法则结合共线定理,从而结合平面向量基本定理,得出
,因为再利用数量积求向量的模的公式结合数量积的定义,得出 ,再利用数量积求向量的模的公式结合数量积的定义和数量积的运算法则,从而求出 ,进而求出线段AO的长度。
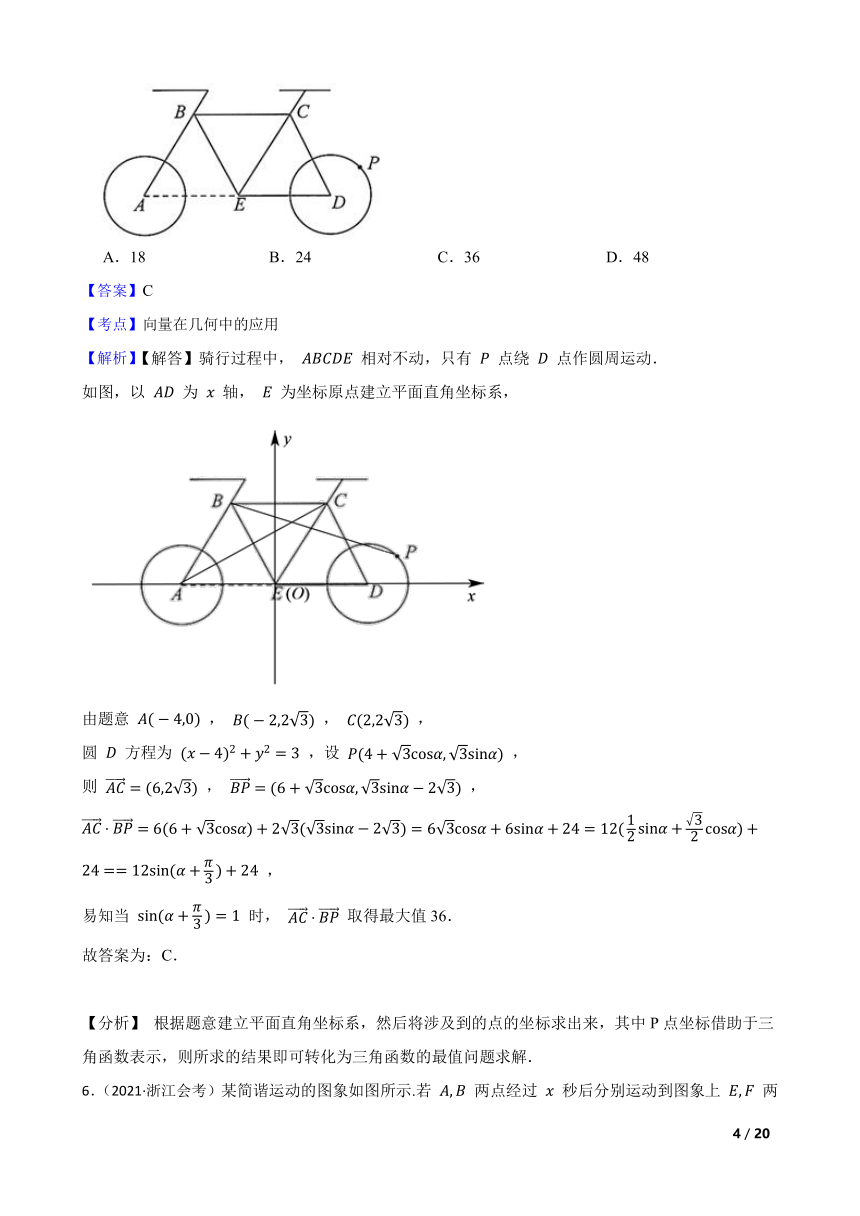
5.(2021·深圳模拟)骑自行车是一种能有效改善心肺功能的耐力性有氧运动,深受大众喜爱,如图是某一自行车的平面结构示意图,已知图中的圆A(前轮),圆D(后轮)的半径均为 , , , 均是边长为4的等边三角形.设点P为后轮上的一点,则在骑动该自行车的过程中, 的最大值为( )
A.18 B.24 C.36 D.48
【答案】C
【考点】向量在几何中的应用
【解析】【解答】骑行过程中, 相对不动,只有 点绕 点作圆周运动.
如图,以 为 轴, 为坐标原点建立平面直角坐标系,
由题意 , , ,
圆 方程为 ,设 ,
则 , ,
,
易知当 时, 取得最大值36.
故答案为:C.
【分析】 根据题意建立平面直角坐标系,然后将涉及到的点的坐标求出来,其中P点坐标借助于三角函数表示,则所求的结果即可转化为三角函数的最值问题求解.
6.(2021·浙江会考)某简谐运动的图象如图所示.若 两点经过 秒后分别运动到图象上 两点,则下列结论不一定成立的是( )
A. B.
C. D.
【答案】B
【考点】平面向量数量积的运算;正弦函数的图象;正弦函数的单调性;正弦函数的周期性
【解析】【解答】设 ,
由图知 , ,解得 ,所以 ,
假设 ,则 即 ,
, , , ,
,
对于A: , ,
所以 ,A成立;
对于B: ,
显然 最大值为 , 不成立,B不成立;
对于C: , ,所以 ,C成立;
对于D: ,
所以 ,
因为 ,所以 ,即 ,所以 ,D成立,
故答案为:B
【分析】根据题意由已知条件结合图象求出A以及周期公式由此即可求出,进而求出函数的解析式,设出点E的坐标由此得到点F的坐标,从而求出向量的坐标,由数量积的坐标公式结合三角函数的最值情况对选项逐一判断即可得出答案。
7.(2021高三上·海安开学考)已知单位向量 , 满足 ,则 , 的夹角为( )
A.0° B.45° C.60° D.90°
【答案】A
【考点】平面向量数量积的坐标表示、模、夹角
【解析】【解答】因为 ,
所以 ,解得 或 ,
因为 ,所以 ,
又因为 ,所以 。
故答案为:A
【分析】利用已知条件结合数量积求向量的模的公式,从而结合数量积的运算法则,进而求出数量积的值,再利用数量积的定义结合两向量的夹角的取值范围,进而求出两向量 , 的夹角 。
8.(2021高三上·南溪月考)已知点 是 所在平面内一点,满足 从 内任取一点 ,则点 在 内部的概率为( )
A. B. C. D.
【答案】B
【考点】向量的共线定理;向量的线性运算性质及几何意义;几何概型
【解析】【解答】解:点P是△ABC所在平面内一点,满足
∴,即,
∴AO是AABC边BC的中线;
∴P是AABC三条中线的交点,如图所示:
从△ABC内任取一点Q,则点Q在△PBC内部的概率为
故答案为:B
【分析】根据向量的线性运算及共线定理,结合几何概型的概率公式求解即可.
二、多选题
9.(2021高三下·常州开学考)已知 , 是平面上夹角为 的两个单位向量, 在该平面上,且( ﹣ )·( ﹣ )=0,则下列结论中正确的有( )
A. B.
C. D. , 的夹角是钝角
【答案】B,C
【考点】向量的模;平面向量的综合题
【解析】【解答】如图,
, , , ,则 ,即 ,B符合题意;
,由( ﹣ )·( ﹣ )=0得 ,点 在以 直径的圆上(可以与 重合). 中点是 ,
则 ,A不符合题意;
的最大值为 ,C符合题意;
与 同向,由图, 与 的夹角不可能为钝角.D不符合题意.
故答案为:BC.
【分析】根据由题意知 ( ﹣ ) ( ﹣ ),作图,则C点在以AB为走私的圆周上,进一步通过推理计算得到结果.
10.(2021·漳州模拟)已知 的三个内角 , , 满足 ,则下列结论正确的是( )
A. 是钝角三角形 B.
C.角 的最大值为 D.角 的最大值为
【答案】A,B,C
【考点】两角和与差的正切公式;正弦定理;余弦定理
【解析】【解答】A. 由题得 ,所以 是钝角三角形,故该选项正确;
B. 由题得 是最大角,所以 ,假设 ,所以 ,所以该选项正确;
C.由题得 所以 ,因为 ,所以角 的最大值为 ,所以该选项正确;
D. 由已知得
所以 ,
当 时 , .所以该选项错误.
故答案为:ABC
【分析】 A选项,利用已知条件,运用正弦定理,可得cosC < 0,即可求解;B选项,结合c为△ABC的最大边,以及正弦定理做等量变换,即可求解;C选项,运用余弦定理,以及均值不等式,即可求解;D选项,对原式利用三角函数的两角和公式,可得tanC =- 3tan A,再运用正切函数的两角和公式,可得tan B的表达式,最后对C取特殊值,即可解答.
11.(2021·唐山模拟)将边长为2的正方形 沿对角线 折成直二面角 ,如图所示,点 分别为线段 的中点,则 ( )
A. 与 所成得角为
B.
C.过 且与 平行得平面截四面体 所得截面的面积为
D.四面体 的外接球的表面积为8π
【答案】C,D
【考点】数量积判断两个平面向量的垂直关系;球的体积和表面积;异面直线及其所成的角;空间中直线与直线之间的位置关系
【解析】【解答】如图,取 中点 ,连接 ,
由正方形的性质得 , 均为等腰直角三角形,
所以 ,
所以 是二面角 的平面角,
因为二面角 是直二面角,
所以 ,
所以,如图,以 点为坐标原点,建立空间直角坐标系,
所以 , , , , ,
所以 ,
所以 ,
所以 与 所成得角为 ,A选项错误;
所以 ,所以 ,
所以 不成立,B选项错误;
取 中点 ,连接 ,
由中位线定理得 ,
所以四边形 为平行四边形,且为过 且与 平行得平面截四面体 所得截面,
由于 ,
所以 ,
所以 ,
所以四边形 为矩形,面积为 ,C选项正确;
因为 ,
所以点 即为四面体 的外接球的球心,半径为 ,
所以四面体 的外接球的表面积为 ,D选项正确.
故答案为:CD.
【分析】利用折叠的方法结合已知条件,再利用直二面角的定义和中点的性质,从而求出异面直线所成的角,再利用线线垂直的判断方法、再利用两直线平行结合平面截四面体所得截面的方法,再结合矩形的定义和向量的方法,推出四边形 为矩形,再利用矩形的面积,从而求出过 且与 平行得平面截四面体 所得截面的面积,因为 ,所以点 即为四面体 的外接球的球心,进而求出球的半径,再利用球的表面积公式,从而求出四面体 的外接球的表面积,进而选出正确选项。
12.(2021高二上·温州期中)下列四个结论正确的有 ( )
A.对于任意两个向量 ,若 ,则 或 或
B.若空间中点 满足 ,则 三点共线
C.空间中任意三个向量 都满足
D.对于任意两个向量 , 都有
【答案】A,B
【考点】向量的线性运算性质及几何意义;平面向量数量积的运算;数量积判断两个平面向量的垂直关系
【解析】【解答】对A,若 ,则 或 或 ,A符合题意.
对B,因为 ,
所以 ,
所以 ,
又因为 为公共点,所以 三点共线,B符合题意.
对C,若 为空间向量中的单位向量,且 夹角为 ,
的夹角为 ,
则 , , ,C不符合题意.
对D,因为 ,
当 时, ,D不符合题意.
故答案为:AB
【分析】对A,根据 得到 或 或 ,即可判断A选项的正误;对B,根据题意得到 和 为公共点,即可判断B选项的正误;对C,利用特殊向量,即可判断C选项的正误;对D,根据 ,即可判断D选项的正误。
三、填空题
13.(2021高一下·辽宁期末)如图,正方形 的边长为2, 是线段 上的动点(含端点),则 的取值范围是 .
【答案】
【考点】数量积的坐标表达式;平面向量数量积的运算
【解析】【解答】以A为坐标原点, 为 轴建立平面直角坐标系,如图:
, , , ,且 ,
所以 , ,
所以 .
所以 的取值范围是 .
故答案为:
【分析】根据题意建立直角坐标系求出各个点的坐标以及向量的坐标,然后由数量积的坐标公式结合题意即可求出的取值范围。
14.(2021·渭南模拟)已知平面向量 , 都是单位向量,且 ,则 的值为 .
【答案】
【考点】平面向量数量积的坐标表示、模、夹角
【解析】【解答】因为平面向量 , 都是单位向量,且 ,
所以,根据题意得 。
故答案为: 。
【分析】利用已知条件结合单位向量的定义,再结合数量积求向量的模的公式结合数量积的运算法则和数量积的值,进而求出向量的模。
15.(2021高一下·金湖月考)若三点 , , 共线,则a+b的最小值为 .
【答案】8
【考点】基本不等式;向量的共线定理
【解析】【解答】因为三点 , , , , ,
所以 与 共线,所以 ,则 ,
因为 ,当且仅当 时等号成立,
又 ,故解得 ,所以 时,a+b的最小值为8.
故答案为:8.
【分析】 利用向量共线定理与基本不等式的性质即可得出.
16.(2022高三上·宝山模拟)在三角形中,是中点,,,则 .
【答案】-6
【考点】平面向量的基本定理及其意义;平面向量数量积的运算
【解析】【解答】由三角形中,,,
可得:
,
故答案为: -6
【分析】根据已知条件,结合加、减法的三角形法则,以为基底表示出 , 再计算 的值。
四、解答题
17.(2021高二上·桂林开学考)已知 三边 , , , , .证明:三角形的三个角满足, .
【答案】证明:因为 , , , ,
由余弦定理得
,
因为 ,所以 ,
又因为 ,由正弦定理得
,
即 ,因为 ,
所以 , ,
所以 .
【考点】正弦定理;余弦定理
【解析】【分析】 由余弦定理得,求出 , 由正弦定理得 ,由 求出 , ,即可证得 。
18.(2021高二下·梅州期末)在① ,② ,这两个条件中任选一个作为已知条件,补充到下面的橫线上并作答.
问题: 的内角 , , 的对边分别为 , , ,已知______,
(1)求 :
(2)若 ,求 面积的最大值.
【答案】(1)选择条件①: ,
由正弦定理得: ,
又在 中, ,
,
又 , , , ,
, .
选择条件②: ,
由正弦定理: ,
,
,
即 .
,
.
,
.
(2) , ,
, ,
,(当且仅当 时,等号成立)
由三角形面积公式可知 ,
面积的最大值为
【考点】正弦定理;余弦定理
【解析】【分析】 (1)选①,结合正弦定理及和差角公式进行化简可求tan B,进而可求B;
选② ,由正弦定理及和差角公式进行化简可求tan B,进而可求B;
(2)由 ,可列余弦定理关系式,根据基本不等式可得 ,再根据三角形的面积公式 即可求出最大值。
19.(2021高三上·长治月考)平行四边形ABCD中(图1),∠A=60°,AB=2AD,将△ABD以BD为折痕折起,使得平面 BD⊥平面BCD,如图2.
(1)证明:平面 BC⊥平面 BD;
(2)已知AD=1,点M为线段 C的中点,求点C到平面MDB的距离.
【答案】(1)证明:由余弦定理得 ,
所以 ,所以 ,即 ,
又平面 BD⊥平面BCD,平面 BD 平面BCD , 平面 ,
所以 平面 ,又 平面 ,
所以平面 平面
(2)解:由 ,则 , ,
,
是 中点,所以 ,
由(1)得 , ,所以 , ,
所以 ,而 ,所以 .设 到平面 的距离为 ,
则 ,
所以 ,所以 .
即 到平面 的距离为 .
【考点】棱柱、棱锥、棱台的体积;直线与平面垂直的判定;直线与平面垂直的性质;平面与平面垂直的判定;点、线、面间的距离计算;余弦定理
【解析】【分析】(1)首先由余弦定理计算出便之间的关系,由此得出线线垂直,然后由面面垂直的性质定理和面面垂直的判定定理即可得证出结论。
(2)根据题意由等体积法代入数值计算出,然后由三角形中几何计算关系计算出,再由等体积法代入数值计算出 到平面 的距离。
20.(2021高二上·新郑月考)为响应国家号召,大力发展三农产业,某农户将自己的一块直角三角形地按如图规划成3个功能区: 区域规划建设果园和养殖土鸡土鸭等, 区域规划建设小型鱼塘养鱼供休闲垂钓. 区域规划为农家乐区域,规划建餐厅、儿童小型乐园以及住宿农舍.为安全起见,在农家乐区域 周围筑起护栏.已知 , , , .
(1)若 时,求护栏的长度( 的周长);
(2)为了更大区域的进行养殖和发展三农产业,规划使得农家乐 区域占地面积最小,怎样设计 的大小,使 的面积最小,并求出最小面积是多少?
【答案】(1)解: , , ,所以 ,可得 ,所以 ,由直角三角形可得 ,
在 中,由余弦定理可得
,
则 ,所以 ,所以 ,
因为 ,所以 ,所以 ,
所以护栏的长度( 的周长)为
(2)解:设 ,则 ,
在 中,由正弦定理 ,可得 ,
又在 中,由 ,得 ,
所以
,
,则 ,
所以当且仅当 ,即 时, 的面积取最小值为
【考点】三角函数的最值;正弦定理;余弦定理;三角形中的几何计算
【解析】【分析】(1)利用已知条件结合正切函数的定义,从而求出角B的值,进而求出角A的值,再利用直角三角形的结构特征,从而求出AB的长,再利用余弦定理求出CM的长,再利用勾股定理证出 ,再利用 结合正切函数的定义,从而求出MN的长,进而求出CN的长,再结合三角形的周长公式,从而求出护栏的长度( 的周长)。
(2) 设 ,则 ,在 中,由正弦定理得出CN的长, 在 中,由正弦定理得出CM的长,再利用三角形的面积公式,从而结合角的取值范围结合正弦型函数的图像,从而求出三角形 的面积的最小值。
21.(2021高一下·揭东期末)在①: , ;②: , 为等腰三角形,这两个条件中任选一个,补充在下面的问题中,并进行解答.
在 中,已知 ,且 ,求:
(1) 的值;
(2) 的面积.
【答案】(1)解:选①,∵ ,
由正弦定理得: ,即 ,
解得 ,
所以 ,
即 .
选②,∵ ,且C为钝角.
∴只能A=B,∴ ,
由余弦定理 得: ,解得: .
由正弦定理得: ,即 ,
解得 ,
所以 ,
即 .
(2) ,即 的面积 .
【考点】两角和与差的正弦公式;同角三角函数间的基本关系;正弦定理;余弦定理;三角形中的几何计算
【解析】【分析】 (1)选①,利用已知条件结合三角形中角C的取值范围和同角三角函数基本关系式,从而得出角C的正弦值,再利用正弦定理求出角A的正弦值,再利用三角形中角A的取值范围和同角三角函数基本关系式,进而求出角A的余弦值,再利用三角形中内角和为180度的性质结合诱导公式,进而求出角B的正弦值。选②,利用已知条件结合三角形中角C的取值范围和同角三角函数基本关系式,从而得出角C的正弦值,所以只能A=B,再利用正弦定理得出 ,再利用余弦定理得出c的值,再利用正弦定理得出角A的正弦值,再结合同角三角函数基本关系式,从而求出角A的余弦值,再利用三角形中内角和为180度的性质结合诱导公式,进而求出角B的正弦值。
(2)利用已知条件结合三角形的面积公式,进而求出三角形 的面积 。
22.(2021高二下·茂名期末)在 中,角 , , 的对边分别为 , , 且 .
(1)求角 的大小;
(2)若 的面积为 ,且 的外接圆半径为 ,试判断 的形状,并说明理由.
【答案】(1)由正弦定理及 ,
得 ,
,
即 ,
.
,
,即 .
,
.
(2) 为等边三角形.
理由如下: ,即 ,
,①
的外接圆半径为 ,
.
由余弦定理得 ,即 ,
,②
由①②得 ,
为等边三角形.
【考点】正弦定理;余弦定理
【解析】【分析】 (1 )根据已知条件,结合正弦定理,可得 ,再结合正弦函数的两角和公式,即可求解;
(2)由△ABC的面积为 ,可推得ac= 4,并且△A BC的外接圆半径为 ,结合正弦定理,可得b=2,再运用余弦定理,即可求解.
1 / 1
2021-2022学年高一下学期人教版(2019)
第六章 《平面向量及其应用》 单元能力提升(含详细解析)
一、单选题
1.(2020高二上·新余期末)在 中,若 , , ,则边 的长为( )
A. B. C. D.4
【答案】B
【考点】余弦定理
【解析】【解答】由题意可知: ,
故 或 ,
其中A=0不成立,则 ,
∵AB=2,AC=3,
∴由余弦定理得BC2=AB2+AC2 2AB×AC×cosA=19,
∴ .
故答案为:B.
【分析】 根据辅助角公式求出A的大小,利用余弦定理即可得到结论.
2.(2022·浙江模拟)已知非零向量,,则“”是“”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
【答案】A
【考点】必要条件、充分条件与充要条件的判断;平面向量共线(平行)的坐标表示
【解析】【解答】由,则,故,即充分性成立,
由 ,若 时必要性不成立.
所以“ ”是“ ”的充分不必要条件.
故答案为:A
【分析】根据充分、必要性的定义,结合向量平行的坐标表示判断条件间的推出关系,即可得答案.
3.(2020高二上·泸县期末)设 为坐标原点, , 是双曲线 的焦点,若双曲线上存在点 ,满足 , ,则该双曲线的离心率为( )
A. B. C. D.
【答案】B
【考点】双曲线的定义;双曲线的简单性质;余弦定理
【解析】【解答】由 ,可得 ,
在直角三角形 中, ,所以 ,
在△ 中,由余弦定理得:
,
所以 ,由双曲线定义可得 ,
解得离心率 .
故答案为:B.
【分析】 由题意作出图形,由已知可得OP⊥PF1,再由已知求得|,,然后结合双曲线定义计算出结果即可。
4.(2021高二下·南京开学考)如图,在三棱柱ABC-A1B1C1中,BC1与B1C相交于点O,∠A1AB=∠A1AC= ,∠BAC= ,A1A=3,AB=AC=2,则线段AO的长度为( )
A. B. C. D.
【答案】A
【考点】平面向量的基本定理及其意义;平面向量数量积的含义与物理意义;平面向量数量积的坐标表示、模、夹角;平面向量数量积的运算
【解析】【解答】因为四边形 是平行四边形,
,
,
,
,
,
,
,
即 。
故答案为:A
【分析】因为四边形 是平行四边形,再利用中点的性质结合平行四边形法则,得出
,再利用三角形法则结合共线定理,从而结合平面向量基本定理,得出
,因为再利用数量积求向量的模的公式结合数量积的定义,得出 ,再利用数量积求向量的模的公式结合数量积的定义和数量积的运算法则,从而求出 ,进而求出线段AO的长度。
5.(2021·深圳模拟)骑自行车是一种能有效改善心肺功能的耐力性有氧运动,深受大众喜爱,如图是某一自行车的平面结构示意图,已知图中的圆A(前轮),圆D(后轮)的半径均为 , , , 均是边长为4的等边三角形.设点P为后轮上的一点,则在骑动该自行车的过程中, 的最大值为( )
A.18 B.24 C.36 D.48
【答案】C
【考点】向量在几何中的应用
【解析】【解答】骑行过程中, 相对不动,只有 点绕 点作圆周运动.
如图,以 为 轴, 为坐标原点建立平面直角坐标系,
由题意 , , ,
圆 方程为 ,设 ,
则 , ,
,
易知当 时, 取得最大值36.
故答案为:C.
【分析】 根据题意建立平面直角坐标系,然后将涉及到的点的坐标求出来,其中P点坐标借助于三角函数表示,则所求的结果即可转化为三角函数的最值问题求解.
6.(2021·浙江会考)某简谐运动的图象如图所示.若 两点经过 秒后分别运动到图象上 两点,则下列结论不一定成立的是( )
A. B.
C. D.
【答案】B
【考点】平面向量数量积的运算;正弦函数的图象;正弦函数的单调性;正弦函数的周期性
【解析】【解答】设 ,
由图知 , ,解得 ,所以 ,
假设 ,则 即 ,
, , , ,
,
对于A: , ,
所以 ,A成立;
对于B: ,
显然 最大值为 , 不成立,B不成立;
对于C: , ,所以 ,C成立;
对于D: ,
所以 ,
因为 ,所以 ,即 ,所以 ,D成立,
故答案为:B
【分析】根据题意由已知条件结合图象求出A以及周期公式由此即可求出,进而求出函数的解析式,设出点E的坐标由此得到点F的坐标,从而求出向量的坐标,由数量积的坐标公式结合三角函数的最值情况对选项逐一判断即可得出答案。
7.(2021高三上·海安开学考)已知单位向量 , 满足 ,则 , 的夹角为( )
A.0° B.45° C.60° D.90°
【答案】A
【考点】平面向量数量积的坐标表示、模、夹角
【解析】【解答】因为 ,
所以 ,解得 或 ,
因为 ,所以 ,
又因为 ,所以 。
故答案为:A
【分析】利用已知条件结合数量积求向量的模的公式,从而结合数量积的运算法则,进而求出数量积的值,再利用数量积的定义结合两向量的夹角的取值范围,进而求出两向量 , 的夹角 。
8.(2021高三上·南溪月考)已知点 是 所在平面内一点,满足 从 内任取一点 ,则点 在 内部的概率为( )
A. B. C. D.
【答案】B
【考点】向量的共线定理;向量的线性运算性质及几何意义;几何概型
【解析】【解答】解:点P是△ABC所在平面内一点,满足
∴,即,
∴AO是AABC边BC的中线;
∴P是AABC三条中线的交点,如图所示:
从△ABC内任取一点Q,则点Q在△PBC内部的概率为
故答案为:B
【分析】根据向量的线性运算及共线定理,结合几何概型的概率公式求解即可.
二、多选题
9.(2021高三下·常州开学考)已知 , 是平面上夹角为 的两个单位向量, 在该平面上,且( ﹣ )·( ﹣ )=0,则下列结论中正确的有( )
A. B.
C. D. , 的夹角是钝角
【答案】B,C
【考点】向量的模;平面向量的综合题
【解析】【解答】如图,
, , , ,则 ,即 ,B符合题意;
,由( ﹣ )·( ﹣ )=0得 ,点 在以 直径的圆上(可以与 重合). 中点是 ,
则 ,A不符合题意;
的最大值为 ,C符合题意;
与 同向,由图, 与 的夹角不可能为钝角.D不符合题意.
故答案为:BC.
【分析】根据由题意知 ( ﹣ ) ( ﹣ ),作图,则C点在以AB为走私的圆周上,进一步通过推理计算得到结果.
10.(2021·漳州模拟)已知 的三个内角 , , 满足 ,则下列结论正确的是( )
A. 是钝角三角形 B.
C.角 的最大值为 D.角 的最大值为
【答案】A,B,C
【考点】两角和与差的正切公式;正弦定理;余弦定理
【解析】【解答】A. 由题得 ,所以 是钝角三角形,故该选项正确;
B. 由题得 是最大角,所以 ,假设 ,所以 ,所以该选项正确;
C.由题得 所以 ,因为 ,所以角 的最大值为 ,所以该选项正确;
D. 由已知得
所以 ,
当 时 , .所以该选项错误.
故答案为:ABC
【分析】 A选项,利用已知条件,运用正弦定理,可得cosC < 0,即可求解;B选项,结合c为△ABC的最大边,以及正弦定理做等量变换,即可求解;C选项,运用余弦定理,以及均值不等式,即可求解;D选项,对原式利用三角函数的两角和公式,可得tanC =- 3tan A,再运用正切函数的两角和公式,可得tan B的表达式,最后对C取特殊值,即可解答.
11.(2021·唐山模拟)将边长为2的正方形 沿对角线 折成直二面角 ,如图所示,点 分别为线段 的中点,则 ( )
A. 与 所成得角为
B.
C.过 且与 平行得平面截四面体 所得截面的面积为
D.四面体 的外接球的表面积为8π
【答案】C,D
【考点】数量积判断两个平面向量的垂直关系;球的体积和表面积;异面直线及其所成的角;空间中直线与直线之间的位置关系
【解析】【解答】如图,取 中点 ,连接 ,
由正方形的性质得 , 均为等腰直角三角形,
所以 ,
所以 是二面角 的平面角,
因为二面角 是直二面角,
所以 ,
所以,如图,以 点为坐标原点,建立空间直角坐标系,
所以 , , , , ,
所以 ,
所以 ,
所以 与 所成得角为 ,A选项错误;
所以 ,所以 ,
所以 不成立,B选项错误;
取 中点 ,连接 ,
由中位线定理得 ,
所以四边形 为平行四边形,且为过 且与 平行得平面截四面体 所得截面,
由于 ,
所以 ,
所以 ,
所以四边形 为矩形,面积为 ,C选项正确;
因为 ,
所以点 即为四面体 的外接球的球心,半径为 ,
所以四面体 的外接球的表面积为 ,D选项正确.
故答案为:CD.
【分析】利用折叠的方法结合已知条件,再利用直二面角的定义和中点的性质,从而求出异面直线所成的角,再利用线线垂直的判断方法、再利用两直线平行结合平面截四面体所得截面的方法,再结合矩形的定义和向量的方法,推出四边形 为矩形,再利用矩形的面积,从而求出过 且与 平行得平面截四面体 所得截面的面积,因为 ,所以点 即为四面体 的外接球的球心,进而求出球的半径,再利用球的表面积公式,从而求出四面体 的外接球的表面积,进而选出正确选项。
12.(2021高二上·温州期中)下列四个结论正确的有 ( )
A.对于任意两个向量 ,若 ,则 或 或
B.若空间中点 满足 ,则 三点共线
C.空间中任意三个向量 都满足
D.对于任意两个向量 , 都有
【答案】A,B
【考点】向量的线性运算性质及几何意义;平面向量数量积的运算;数量积判断两个平面向量的垂直关系
【解析】【解答】对A,若 ,则 或 或 ,A符合题意.
对B,因为 ,
所以 ,
所以 ,
又因为 为公共点,所以 三点共线,B符合题意.
对C,若 为空间向量中的单位向量,且 夹角为 ,
的夹角为 ,
则 , , ,C不符合题意.
对D,因为 ,
当 时, ,D不符合题意.
故答案为:AB
【分析】对A,根据 得到 或 或 ,即可判断A选项的正误;对B,根据题意得到 和 为公共点,即可判断B选项的正误;对C,利用特殊向量,即可判断C选项的正误;对D,根据 ,即可判断D选项的正误。
三、填空题
13.(2021高一下·辽宁期末)如图,正方形 的边长为2, 是线段 上的动点(含端点),则 的取值范围是 .
【答案】
【考点】数量积的坐标表达式;平面向量数量积的运算
【解析】【解答】以A为坐标原点, 为 轴建立平面直角坐标系,如图:
, , , ,且 ,
所以 , ,
所以 .
所以 的取值范围是 .
故答案为:
【分析】根据题意建立直角坐标系求出各个点的坐标以及向量的坐标,然后由数量积的坐标公式结合题意即可求出的取值范围。
14.(2021·渭南模拟)已知平面向量 , 都是单位向量,且 ,则 的值为 .
【答案】
【考点】平面向量数量积的坐标表示、模、夹角
【解析】【解答】因为平面向量 , 都是单位向量,且 ,
所以,根据题意得 。
故答案为: 。
【分析】利用已知条件结合单位向量的定义,再结合数量积求向量的模的公式结合数量积的运算法则和数量积的值,进而求出向量的模。
15.(2021高一下·金湖月考)若三点 , , 共线,则a+b的最小值为 .
【答案】8
【考点】基本不等式;向量的共线定理
【解析】【解答】因为三点 , , , , ,
所以 与 共线,所以 ,则 ,
因为 ,当且仅当 时等号成立,
又 ,故解得 ,所以 时,a+b的最小值为8.
故答案为:8.
【分析】 利用向量共线定理与基本不等式的性质即可得出.
16.(2022高三上·宝山模拟)在三角形中,是中点,,,则 .
【答案】-6
【考点】平面向量的基本定理及其意义;平面向量数量积的运算
【解析】【解答】由三角形中,,,
可得:
,
故答案为: -6
【分析】根据已知条件,结合加、减法的三角形法则,以为基底表示出 , 再计算 的值。
四、解答题
17.(2021高二上·桂林开学考)已知 三边 , , , , .证明:三角形的三个角满足, .
【答案】证明:因为 , , , ,
由余弦定理得
,
因为 ,所以 ,
又因为 ,由正弦定理得
,
即 ,因为 ,
所以 , ,
所以 .
【考点】正弦定理;余弦定理
【解析】【分析】 由余弦定理得,求出 , 由正弦定理得 ,由 求出 , ,即可证得 。
18.(2021高二下·梅州期末)在① ,② ,这两个条件中任选一个作为已知条件,补充到下面的橫线上并作答.
问题: 的内角 , , 的对边分别为 , , ,已知______,
(1)求 :
(2)若 ,求 面积的最大值.
【答案】(1)选择条件①: ,
由正弦定理得: ,
又在 中, ,
,
又 , , , ,
, .
选择条件②: ,
由正弦定理: ,
,
,
即 .
,
.
,
.
(2) , ,
, ,
,(当且仅当 时,等号成立)
由三角形面积公式可知 ,
面积的最大值为
【考点】正弦定理;余弦定理
【解析】【分析】 (1)选①,结合正弦定理及和差角公式进行化简可求tan B,进而可求B;
选② ,由正弦定理及和差角公式进行化简可求tan B,进而可求B;
(2)由 ,可列余弦定理关系式,根据基本不等式可得 ,再根据三角形的面积公式 即可求出最大值。
19.(2021高三上·长治月考)平行四边形ABCD中(图1),∠A=60°,AB=2AD,将△ABD以BD为折痕折起,使得平面 BD⊥平面BCD,如图2.
(1)证明:平面 BC⊥平面 BD;
(2)已知AD=1,点M为线段 C的中点,求点C到平面MDB的距离.
【答案】(1)证明:由余弦定理得 ,
所以 ,所以 ,即 ,
又平面 BD⊥平面BCD,平面 BD 平面BCD , 平面 ,
所以 平面 ,又 平面 ,
所以平面 平面
(2)解:由 ,则 , ,
,
是 中点,所以 ,
由(1)得 , ,所以 , ,
所以 ,而 ,所以 .设 到平面 的距离为 ,
则 ,
所以 ,所以 .
即 到平面 的距离为 .
【考点】棱柱、棱锥、棱台的体积;直线与平面垂直的判定;直线与平面垂直的性质;平面与平面垂直的判定;点、线、面间的距离计算;余弦定理
【解析】【分析】(1)首先由余弦定理计算出便之间的关系,由此得出线线垂直,然后由面面垂直的性质定理和面面垂直的判定定理即可得证出结论。
(2)根据题意由等体积法代入数值计算出,然后由三角形中几何计算关系计算出,再由等体积法代入数值计算出 到平面 的距离。
20.(2021高二上·新郑月考)为响应国家号召,大力发展三农产业,某农户将自己的一块直角三角形地按如图规划成3个功能区: 区域规划建设果园和养殖土鸡土鸭等, 区域规划建设小型鱼塘养鱼供休闲垂钓. 区域规划为农家乐区域,规划建餐厅、儿童小型乐园以及住宿农舍.为安全起见,在农家乐区域 周围筑起护栏.已知 , , , .
(1)若 时,求护栏的长度( 的周长);
(2)为了更大区域的进行养殖和发展三农产业,规划使得农家乐 区域占地面积最小,怎样设计 的大小,使 的面积最小,并求出最小面积是多少?
【答案】(1)解: , , ,所以 ,可得 ,所以 ,由直角三角形可得 ,
在 中,由余弦定理可得
,
则 ,所以 ,所以 ,
因为 ,所以 ,所以 ,
所以护栏的长度( 的周长)为
(2)解:设 ,则 ,
在 中,由正弦定理 ,可得 ,
又在 中,由 ,得 ,
所以
,
,则 ,
所以当且仅当 ,即 时, 的面积取最小值为
【考点】三角函数的最值;正弦定理;余弦定理;三角形中的几何计算
【解析】【分析】(1)利用已知条件结合正切函数的定义,从而求出角B的值,进而求出角A的值,再利用直角三角形的结构特征,从而求出AB的长,再利用余弦定理求出CM的长,再利用勾股定理证出 ,再利用 结合正切函数的定义,从而求出MN的长,进而求出CN的长,再结合三角形的周长公式,从而求出护栏的长度( 的周长)。
(2) 设 ,则 ,在 中,由正弦定理得出CN的长, 在 中,由正弦定理得出CM的长,再利用三角形的面积公式,从而结合角的取值范围结合正弦型函数的图像,从而求出三角形 的面积的最小值。
21.(2021高一下·揭东期末)在①: , ;②: , 为等腰三角形,这两个条件中任选一个,补充在下面的问题中,并进行解答.
在 中,已知 ,且 ,求:
(1) 的值;
(2) 的面积.
【答案】(1)解:选①,∵ ,
由正弦定理得: ,即 ,
解得 ,
所以 ,
即 .
选②,∵ ,且C为钝角.
∴只能A=B,∴ ,
由余弦定理 得: ,解得: .
由正弦定理得: ,即 ,
解得 ,
所以 ,
即 .
(2) ,即 的面积 .
【考点】两角和与差的正弦公式;同角三角函数间的基本关系;正弦定理;余弦定理;三角形中的几何计算
【解析】【分析】 (1)选①,利用已知条件结合三角形中角C的取值范围和同角三角函数基本关系式,从而得出角C的正弦值,再利用正弦定理求出角A的正弦值,再利用三角形中角A的取值范围和同角三角函数基本关系式,进而求出角A的余弦值,再利用三角形中内角和为180度的性质结合诱导公式,进而求出角B的正弦值。选②,利用已知条件结合三角形中角C的取值范围和同角三角函数基本关系式,从而得出角C的正弦值,所以只能A=B,再利用正弦定理得出 ,再利用余弦定理得出c的值,再利用正弦定理得出角A的正弦值,再结合同角三角函数基本关系式,从而求出角A的余弦值,再利用三角形中内角和为180度的性质结合诱导公式,进而求出角B的正弦值。
(2)利用已知条件结合三角形的面积公式,进而求出三角形 的面积 。
22.(2021高二下·茂名期末)在 中,角 , , 的对边分别为 , , 且 .
(1)求角 的大小;
(2)若 的面积为 ,且 的外接圆半径为 ,试判断 的形状,并说明理由.
【答案】(1)由正弦定理及 ,
得 ,
,
即 ,
.
,
,即 .
,
.
(2) 为等边三角形.
理由如下: ,即 ,
,①
的外接圆半径为 ,
.
由余弦定理得 ,即 ,
,②
由①②得 ,
为等边三角形.
【考点】正弦定理;余弦定理
【解析】【分析】 (1 )根据已知条件,结合正弦定理,可得 ,再结合正弦函数的两角和公式,即可求解;
(2)由△ABC的面积为 ,可推得ac= 4,并且△A BC的外接圆半径为 ,结合正弦定理,可得b=2,再运用余弦定理,即可求解.
1 / 1
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
