精讲精练·专项突破 第六章《平面向量及其应用》单元能力提升(含详细解析) (53)
文档属性
| 名称 | 精讲精练·专项突破 第六章《平面向量及其应用》单元能力提升(含详细解析) (53) |  | |
| 格式 | docx | ||
| 文件大小 | 112.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-18 16:27:35 | ||
图片预览




文档简介
精讲精练·专项突破
2021-2022学年高一下学期人教版(2019)
第六章 《平面向量及其应用》 单元能力提升(含详细解析)
一、单选题
1.(2020高二上·荔湾期末)已知向量 ,且 与 平行,则 的值是( )
A. B. C.-3 D.3
2.(2020高二上·新乡期末)在 中,角 , , 所对的边分别为 , , , 的面积为 ,且 , , ,则 ( )
A. B. C. D.
3.(2021·湖南模拟)已知 ,设函数 ,当 时, 取得最小值,则 在 方向上的投影为( )
A. B. C. D.
4.(2021高二上·大同期末)在正方体中,M为棱的中点,则直线AM与平面所成角的正弦值为( )
A. B. C. D.
5.如图,在直角梯形 中, , , , , 是线段 上的动点,则 的最小值为( )
A. B.6 C. D.4
6.(2021高二下·浙江期末)已知平面向量 , , ,满足 , 对任意实数 恒成立, ,则 的最大值为( )
A. B. C. D.
7.(2021高一下·运城期末)已知向量 , , 满足 , , 与 的夹角为 , ,则 的最大值为( )
A. B. C. D.
8.(2021高一下·浙江期中)已知平行四边形,若,,且交于点,则( )
A. B. C. D.
二、多选题
9.(2021高二上·越秀期末)已知点P是所在平面外一点,若,则( )
A. B. C. D.
10.(2021高一下·浙江月考)下列命题中正确的是( )
A.若 ,则
B.
C.若向量 、 是非零向量,则 与 的方向相同
D.若 ,则存在唯一实数 使得
11.(2021高二上·滕州期中)如图,一个结晶体的形状为平行六面体ABCD-A1B1C1D1,其中,以顶点A为端点的三条棱长均为6,且它们彼此的夹角都是60°,下列说法中正确的是( )
A.AC1=6
B.AC1⊥DB
C.向量与的夹角是60°
D.BD1与AC所成角的余弦值为
12.(2021·青岛模拟)已知 , ,若 与 共线,则下列说法正确的是( )
A.将 的图象向左平移 个单位得到函数 的图象
B.函数 的最小正周期为
C.直线 是 的一条对称轴
D.函数 在 上单调递减
三、填空题
13.(2021·广东模拟)已知向量 ,若 与 共线,则m = .
14.(2021·马鞍山模拟)已知平面向量 , ,若 ,则实数 的值为 .
15.(2020高三上·德州期末)《数书九章》是中国南宋时期杰出数学家秦九韶的著作,全书十八卷共八十一个问题,分为九类,每类九个问题《数书九章》中记录了秦九解的许多创造性成就,其中在卷五“三斜求积”中提出了已知三角形三边a,b,c求面积的公式,这与古希腊的海伦公式完全等价,其求法是:“以小斜幂并大斜幂减中斜幂,余半之,自乘于上,以小斜幂乘大斜幂减上,余四约之,为实,一为从隅,开平方得积”若把以上这段文字写成公式,即 S为三角形的面积,a,b,c为三角形的三边长,现有 满足 且 ,则 的外接圆的半径为 .
16.(2020高二上·赣县期末)长方体 中, ,设点 关于直线 对称点为 ,则点 与点 之间的距离是
四、解答题
17.(2021高一下·江苏期中)在 中,a,b,c分别是角A,B,C的对应边,已知 .
(1)求A;
(2)若 , ,求 的面积.
18.(2021高三上·邢台月考)在 中,内角A、B、C所对的边分别为a、b、c, .
(1)求A;
(2)若 的面积为 , ,求c.
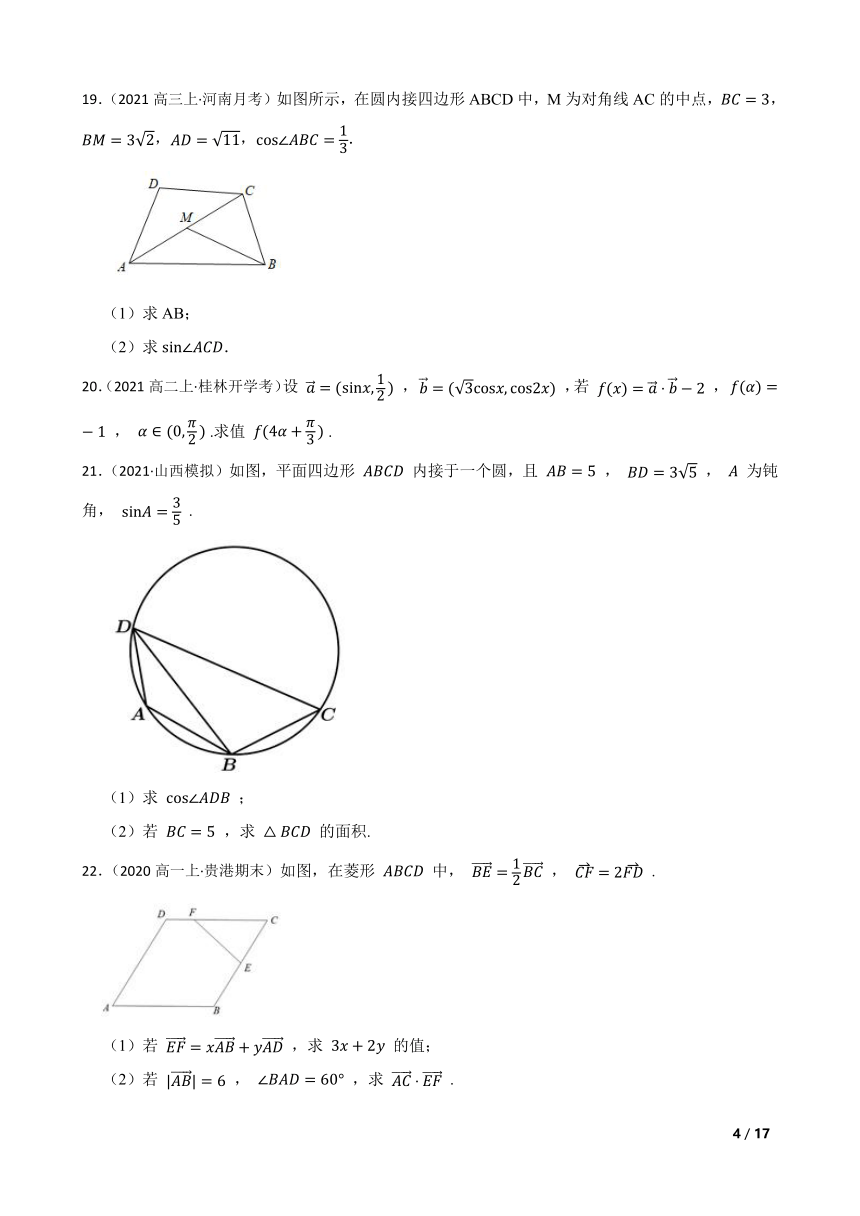
19.(2021高三上·河南月考)如图所示,在圆内接四边形ABCD中,M为对角线AC的中点,,,,.
(1)求AB;
(2)求.
20.(2021高二上·桂林开学考)设 , ,若 , , .求值 .
21.(2021·山西模拟)如图,平面四边形 内接于一个圆,且 , , 为钝角, .
(1)求 ;
(2)若 ,求 的面积.
22.(2020高一上·贵港期末)如图,在菱形 中, , .
(1)若 ,求 的值;
(2)若 , ,求 .
答案解析部分
1.【答案】D
【考点】平面向量共线(平行)的坐标表示
【解析】【解答】解:因为向量 ,
所以 , , ,
又 与 平行,
所以存在实数 ,使得 ,
即 , , ,6, ,
则 ,解得 .
故答案为:D.
【分析】 利用已知向量,先求出 的坐标,然后.再利用向量共线定理,得到,再根据向量相等的坐标表示,列出方程组求解即可.
2.【答案】D
【考点】两角和与差的余弦公式;同角三角函数间的基本关系;解三角形;余弦定理
【解析】【解答】因为 ,所以 ,
所以 ,所以 .
由 ,得 ,
所以 .
故答案为:D
【分析】根据题意由两角和的余弦公式整理化简即可求出cosC的值,结合同角三角函数的基本关系上即可求出sinC的值,再把结果代入到余弦定理计算出,由此计算出三角形的面积即可。
3.【答案】D
【考点】向量的模;向量的投影
【解析】【解答】解:,
令,则当时,g(t)取得最小值,此时f(t)取得最小值,故,所以 在 方向上的投影为
故答案为:D
【分析】由向量的求模公式,结合二次函数的最值问题,根据向量的投影公式求解即可
4.【答案】B
【考点】数量积表示两个向量的夹角;直线与平面所成的角;用空间向量求直线与平面的夹角
【解析】【解答】解:不妨设正方体的棱长为2,连接,以为坐标原点如图建立空间直角坐标系,
则,0,,,2,,,1,,,,
由于平面,平面,故,
又正方形,故,
,,平面,
故平面,
所以为平面的一个法向量,
,
故直线与平面所成角的正弦值为.
故答案为:B.
【分析】根据题意建立空间直角坐标系,求出各个点的坐标然后由数量积的坐标公式即可求出平面的法向量,然后由线面角与向量夹角的关系,把坐标代入到数量积公式计算出结果即可。
5.【答案】B
【考点】向量的模;平面向量的坐标运算
【解析】【解答】解:如图,以 点为坐标原点,建立平面直角坐标系,设 , ,
因为 , ,
所以 ,
所以 , ,
所以 ,
所以 ,
所以当 ,即 时, 的最小值为6.
故答案为:B
【分析】以 点为坐标原点,建立平面直角坐标系,设 , ,则,结合平面向量的坐标运算推出,故当时,可得 的最小值 .
6.【答案】D
【考点】两向量的和或差的模的最值;平面向量的坐标运算;两点间的距离公式
【解析】【解答】解:由 ,
得 ,
即 ,
因为 对任意实数 恒成立,
所以 ,
解得 ,
所以 即 ,
由 ,可设 ,
则 , ,
因为 ,
所以 ,即 ,
所以向量 对应点的坐标的轨迹方程是以 为圆心, 为半径的圆,
,可以看成 和 两点之间的距离,
将 代入 ,得 在圆内,
圆心 到点 的距离为 ,
所以 的最大值为 .
故答案为:D.
【分析】根据题意整理化简原式由此得到,再由已知条件结合向量的坐标公式整理得出,,由一直听结合数量积的坐标公式整理得到向量 对应点的坐标的轨迹方程是以 为圆心, 为半径的圆,然后由向量模的公式以及两点间的距离公式整理得出答案即可。
7.【答案】B
【考点】平面向量数量积的运算;圆方程的综合应用
【解析】【解答】设 , , ,
以OA所在的直线为x轴,O为坐标原点建立平面直角坐标系,
因为 , , 与 的夹角为 ,
所以 , ,设 ,
因为 ,所以 ,即 ,
圆心坐标为 ,半径 ,
表示点C到坐标原点的距离即为圆上的点到坐标原点的距离,
因为圆心 到原点的距离为 ,所以 .
故答案为:B.
【分析】设 , , ,以OA所在的直线为x轴,O为坐标原点建立平面直角坐标系,及向量的数量积的坐标表示整理出x, y的关系,结合圆的性质及几何意义可求答案。
8.【答案】B
【考点】向量的共线定理;向量的线性运算性质及几何意义
【解析】【解答】设,又因为,
设,则,则,解得,所以,
故答案为:B.
【分析】结合图形得性质以及平面向量的线性运算,求得与,然后根据 与 共线,得到方程组,解之即可.
9.【答案】B,C,D
【考点】向量的模;空间中的点的坐标
【解析】【解答】解:对A,,所以不成立,A不符合题意;
对于B,,
则,所以,B符合题意;
对于C,,C符合题意;
对于D,,则,D符合题意.
故答案为:BCD.
【分析】根据题意由空间数量积、向量模的坐标公式,代入数值计算出结果由此对选项逐一判断即可得出答案。
10.【答案】B,C
【考点】平行向量与共线向量;向量加减混合运算及其几何意义;向量的共线定理
【解析】【解答】对于A选项,由于向量不能比大小,A选项错误;
对于B选项, ,B选项正确;
对于C选项,已知向量 、 是非零向量, 、 的方向相同,C选项正确;
对于D选项,若 , ,则 ,但不存在实数 使得 ,D选项错误.
故答案为:BC.
【分析】由平面向量不能比较大小即可判断出选项A错误,由平面向量的加减法运算法则即可判断出选项B正确,由平面向量的线性运算即可判断出选项C正确,由特殊值法即可判断出选项D错误;由此即可得出答案。
11.【答案】A,B
【考点】平面向量数量积的坐标表示、模、夹角;数量积表示两个向量的夹角;异面直线及其所成的角;空间中直线与直线之间的位置关系
【解析】【解答】因为以顶点A为端点的三条棱长均为6,且它们彼此的夹角都是60°,
所以·=·=·=6×6×cos 60°=18,
(++)2=+++2·+2·+2·
=36+36+36+3×2×18=216,
则||=|++|=6, 所以A符合题意;
·=(++)·(-)
=·-·+-·+·- =0,所以B符合题意;
显然△AA1D 为等边三角形,则∠AA1D=60°.
因为=,且向量与的夹角是120°,所以与的夹角是120°,所以C不正确;
因为=+-=+ ,
所以||==6,||==6,
·=(+-)·(+)=36,
所以cos<>===,所以D不正确.
故答案为::AB.
【分析】以顶点A为端点的三条棱长均为6,且它们彼此的夹角都是60°,再利用数量积的定义得出·=·=·=18,再利用平行四边形法则和数量积求向量的模的公式,得出||的值;再利用数量积的运算法则结合数量积的定义,得出·=0,再利用数量积为0两向量垂直的等价关系,从而证出 AC1⊥DB ;再利用三角形△AA1D 为等边三角形,则∠AA1D=60°,再由=,且向量与的夹角是120°,从而求出与的夹角;再利用平面向量基本定理结合数量积求向量的模的公式,得出||和|的值,再利用数量积的运算法则求出数量积的值,再结合数量积求向量夹角公式,进而求出BD1与AC所成角的余弦值,从而找出说法正确的选项。
12.【答案】B,C
【考点】向量在几何中的应用
【解析】【解答】因为 与 共线,则 ,
所以
.
对于A,将 的图象向左平移 个单位得到函数
的图象,A不符合题意;
对于B, ,B符合题意;
对于C,当 时,则 ,
由余弦函数的对称轴为 ,C符合题意;
对于D, ,则 ,
由余弦函数的单调递增区间为 ,
当 时,余弦函数的单调递增区间为 ,
所以函数 在 上单调递增.
故答案为:BC
【分析】 根据向量共线建立方程关系,利用三角函数关系进行化简求出函数 的解析式,分别进行判断即可.
13.【答案】-4
【考点】平面向量共线(平行)的坐标表示
【解析】【解答】因为向量 ,且 与 共线,
所以 ,
解得: ,
故答案为:-4.
【分析】根据两个向量共线的性质,可得 ,解方程求得m的值。
14.【答案】
【考点】平面向量共线(平行)的坐标表示
【解析】【解答】因为 , ,所以 ,
因为 ,所以 ,解得 ,
故答案为: .
【分析】数学由向量的坐标公式求出,再由共线向量的坐标公式代入数值计算出结果即可。
15.【答案】
【考点】正弦定理;三角形中的几何计算
【解析】【解答】由已知和正弦定理得: ,
设 ,
由 ,
解得 ,所以 ,设 的外接圆的半径为 ,
由 ,解得 ,
由正弦定理得 ,所以 。
故答案为: 。
【分析】由已知和正弦定理得的比值,进而设 ,再利用已知的三角形面积公式,即 ,进而结合已知条件求出t的值,进而求出边长a,b,c的长,设 的外接圆的半径为 ,再利用三角形 的面积公式结合已知条件,进而求出角A的正弦值,再利用正弦定理的性质,进而求出三角形 的外接圆的半径。
16.【答案】1
【考点】余弦定理
【解析】【解答】画出过点 ,线段 的平面图如图所示:过点 作 于点 ,
因为 点是点 关于直线 对称点,所以 且 平分 ,
所以 ,
因为长方体 中, ,
所以 , , ,
所以 , ,所以
, ,
在 中由余弦定理得
,
故答案为:1
【分析】根据几何体画出平面图形,根据边长得出角的大小,转化到中, , ,根据条件运用余弦定理求解即可。
17.【答案】(1)由 ,根据正弦定理可得: ,则 ,
所以 ,
因为 ,所以 ,则 ;
(2)由(1)知 ,则 ,
所以 或 ,即 或 ,
因为 为三角形内角,所以 ;
因此 ,
所以 ,
因此 ,
所以 ,
又 ,根据正弦定理可得 ,则 ,
因此 的面积为 .
【考点】两角和与差的正弦公式;同角三角函数间的基本关系;正弦定理;余弦定理
【解析】【分析】(1)首先由正弦定理,以及两角和的正弦公式整理得到,由此得出
,从而求出角A的大小。
(2)由(1) 的结论以及角的取值范围,结合同角三角函数的基本关系时即可得出,再由两角和的正弦公式求出sinB的值,从而得出cosB的值,结合三角形的内角和性质以及两角和的正弦公式代入数值即可计算出sinC的值,然后由正弦定理计算出b的值,结合三角形的面积公式计算出结果即可。
18.【答案】(1)解:由正弦定理有, ,得
由余弦定理有
又由 ,可得
(2)解:由题意有
由正弦定理有 ,
由 ,有
由 ,有 ,可得
由正弦定理得
【考点】解三角形;正弦定理;余弦定理
【解析】【分析】(1)根据题意由正弦定理整理即可得出,然后由余弦定理代入数值计算出cosA的值,结合角的取值范围即可求出角A的大小。
(2)由已知条件结合正弦定理整理即可得到,结合题意即可求出,由此即可得出,结合正弦定理代入数值计算出结果即可。
19.【答案】(1)解:根据题意,,
两边平方得,即,
解得或(舍去),即.
(2)解:由余弦定理可得,所以,
由题意知,所以,所以.
根据正弦定理得,
因此
【考点】平面向量数量积的运算;正弦定理;余弦定理
【解析】【分析】(1)由 ,两边平方,解方程得出AB的值;
(2)由于弦定理得出AC,再由圆内接四边形的性质以及正弦定理得出.
20.【答案】解:
由 ,即
所以 ,由 ,则
所以 ,则
故 .
【考点】平面向量数量积的运算;正弦函数的单调性;诱导公式
【解析】【分析】 先用数量积公式得到f (x),化成辅助角形式,然后利用正弦函数的性质求出a,再由诱导公式计算求值即可.
21.【答案】(1)在 中, , , ,
由正弦定理可得 ,即 ,解得 ;
又A为钝角,所以 为锐角,则 ;
(2)由平面四边形 内接于一个圆可得 ,所以 ,
又A为钝角,所以 为锐角,则 ,
在 中,由余弦定理可得 ,
即 ,整理得 ,
解得 ,
则 的面积为 .
【考点】正弦定理;余弦定理
【解析】【分析】(1) 根据已知条件,在△ABD中,运用正弦定理,即可求解;
(2)根据已知条件,运用余弦定理,以及三角形面积公式,即可求解.
22.【答案】(1)解:因为 , ,
所以 ,
所以 , ,故 .
(2)解:∵ ,
∴ ,
∵ 为菱形,∴ ,
∴ ,即 .
【考点】向量的线性运算性质及几何意义;平面向量数量积的运算
【解析】【分析】 (1)结合向量线性运算的几何意义,用 表示出向量 ,即可求出x, y的值,进而求出 的值;
(2)将 用表示,结合已知求得 , ,然后结合数量积的定义求解即可求出 .
1 / 1
2021-2022学年高一下学期人教版(2019)
第六章 《平面向量及其应用》 单元能力提升(含详细解析)
一、单选题
1.(2020高二上·荔湾期末)已知向量 ,且 与 平行,则 的值是( )
A. B. C.-3 D.3
2.(2020高二上·新乡期末)在 中,角 , , 所对的边分别为 , , , 的面积为 ,且 , , ,则 ( )
A. B. C. D.
3.(2021·湖南模拟)已知 ,设函数 ,当 时, 取得最小值,则 在 方向上的投影为( )
A. B. C. D.
4.(2021高二上·大同期末)在正方体中,M为棱的中点,则直线AM与平面所成角的正弦值为( )
A. B. C. D.
5.如图,在直角梯形 中, , , , , 是线段 上的动点,则 的最小值为( )
A. B.6 C. D.4
6.(2021高二下·浙江期末)已知平面向量 , , ,满足 , 对任意实数 恒成立, ,则 的最大值为( )
A. B. C. D.
7.(2021高一下·运城期末)已知向量 , , 满足 , , 与 的夹角为 , ,则 的最大值为( )
A. B. C. D.
8.(2021高一下·浙江期中)已知平行四边形,若,,且交于点,则( )
A. B. C. D.
二、多选题
9.(2021高二上·越秀期末)已知点P是所在平面外一点,若,则( )
A. B. C. D.
10.(2021高一下·浙江月考)下列命题中正确的是( )
A.若 ,则
B.
C.若向量 、 是非零向量,则 与 的方向相同
D.若 ,则存在唯一实数 使得
11.(2021高二上·滕州期中)如图,一个结晶体的形状为平行六面体ABCD-A1B1C1D1,其中,以顶点A为端点的三条棱长均为6,且它们彼此的夹角都是60°,下列说法中正确的是( )
A.AC1=6
B.AC1⊥DB
C.向量与的夹角是60°
D.BD1与AC所成角的余弦值为
12.(2021·青岛模拟)已知 , ,若 与 共线,则下列说法正确的是( )
A.将 的图象向左平移 个单位得到函数 的图象
B.函数 的最小正周期为
C.直线 是 的一条对称轴
D.函数 在 上单调递减
三、填空题
13.(2021·广东模拟)已知向量 ,若 与 共线,则m = .
14.(2021·马鞍山模拟)已知平面向量 , ,若 ,则实数 的值为 .
15.(2020高三上·德州期末)《数书九章》是中国南宋时期杰出数学家秦九韶的著作,全书十八卷共八十一个问题,分为九类,每类九个问题《数书九章》中记录了秦九解的许多创造性成就,其中在卷五“三斜求积”中提出了已知三角形三边a,b,c求面积的公式,这与古希腊的海伦公式完全等价,其求法是:“以小斜幂并大斜幂减中斜幂,余半之,自乘于上,以小斜幂乘大斜幂减上,余四约之,为实,一为从隅,开平方得积”若把以上这段文字写成公式,即 S为三角形的面积,a,b,c为三角形的三边长,现有 满足 且 ,则 的外接圆的半径为 .
16.(2020高二上·赣县期末)长方体 中, ,设点 关于直线 对称点为 ,则点 与点 之间的距离是
四、解答题
17.(2021高一下·江苏期中)在 中,a,b,c分别是角A,B,C的对应边,已知 .
(1)求A;
(2)若 , ,求 的面积.
18.(2021高三上·邢台月考)在 中,内角A、B、C所对的边分别为a、b、c, .
(1)求A;
(2)若 的面积为 , ,求c.
19.(2021高三上·河南月考)如图所示,在圆内接四边形ABCD中,M为对角线AC的中点,,,,.
(1)求AB;
(2)求.
20.(2021高二上·桂林开学考)设 , ,若 , , .求值 .
21.(2021·山西模拟)如图,平面四边形 内接于一个圆,且 , , 为钝角, .
(1)求 ;
(2)若 ,求 的面积.
22.(2020高一上·贵港期末)如图,在菱形 中, , .
(1)若 ,求 的值;
(2)若 , ,求 .
答案解析部分
1.【答案】D
【考点】平面向量共线(平行)的坐标表示
【解析】【解答】解:因为向量 ,
所以 , , ,
又 与 平行,
所以存在实数 ,使得 ,
即 , , ,6, ,
则 ,解得 .
故答案为:D.
【分析】 利用已知向量,先求出 的坐标,然后.再利用向量共线定理,得到,再根据向量相等的坐标表示,列出方程组求解即可.
2.【答案】D
【考点】两角和与差的余弦公式;同角三角函数间的基本关系;解三角形;余弦定理
【解析】【解答】因为 ,所以 ,
所以 ,所以 .
由 ,得 ,
所以 .
故答案为:D
【分析】根据题意由两角和的余弦公式整理化简即可求出cosC的值,结合同角三角函数的基本关系上即可求出sinC的值,再把结果代入到余弦定理计算出,由此计算出三角形的面积即可。
3.【答案】D
【考点】向量的模;向量的投影
【解析】【解答】解:,
令,则当时,g(t)取得最小值,此时f(t)取得最小值,故,所以 在 方向上的投影为
故答案为:D
【分析】由向量的求模公式,结合二次函数的最值问题,根据向量的投影公式求解即可
4.【答案】B
【考点】数量积表示两个向量的夹角;直线与平面所成的角;用空间向量求直线与平面的夹角
【解析】【解答】解:不妨设正方体的棱长为2,连接,以为坐标原点如图建立空间直角坐标系,
则,0,,,2,,,1,,,,
由于平面,平面,故,
又正方形,故,
,,平面,
故平面,
所以为平面的一个法向量,
,
故直线与平面所成角的正弦值为.
故答案为:B.
【分析】根据题意建立空间直角坐标系,求出各个点的坐标然后由数量积的坐标公式即可求出平面的法向量,然后由线面角与向量夹角的关系,把坐标代入到数量积公式计算出结果即可。
5.【答案】B
【考点】向量的模;平面向量的坐标运算
【解析】【解答】解:如图,以 点为坐标原点,建立平面直角坐标系,设 , ,
因为 , ,
所以 ,
所以 , ,
所以 ,
所以 ,
所以当 ,即 时, 的最小值为6.
故答案为:B
【分析】以 点为坐标原点,建立平面直角坐标系,设 , ,则,结合平面向量的坐标运算推出,故当时,可得 的最小值 .
6.【答案】D
【考点】两向量的和或差的模的最值;平面向量的坐标运算;两点间的距离公式
【解析】【解答】解:由 ,
得 ,
即 ,
因为 对任意实数 恒成立,
所以 ,
解得 ,
所以 即 ,
由 ,可设 ,
则 , ,
因为 ,
所以 ,即 ,
所以向量 对应点的坐标的轨迹方程是以 为圆心, 为半径的圆,
,可以看成 和 两点之间的距离,
将 代入 ,得 在圆内,
圆心 到点 的距离为 ,
所以 的最大值为 .
故答案为:D.
【分析】根据题意整理化简原式由此得到,再由已知条件结合向量的坐标公式整理得出,,由一直听结合数量积的坐标公式整理得到向量 对应点的坐标的轨迹方程是以 为圆心, 为半径的圆,然后由向量模的公式以及两点间的距离公式整理得出答案即可。
7.【答案】B
【考点】平面向量数量积的运算;圆方程的综合应用
【解析】【解答】设 , , ,
以OA所在的直线为x轴,O为坐标原点建立平面直角坐标系,
因为 , , 与 的夹角为 ,
所以 , ,设 ,
因为 ,所以 ,即 ,
圆心坐标为 ,半径 ,
表示点C到坐标原点的距离即为圆上的点到坐标原点的距离,
因为圆心 到原点的距离为 ,所以 .
故答案为:B.
【分析】设 , , ,以OA所在的直线为x轴,O为坐标原点建立平面直角坐标系,及向量的数量积的坐标表示整理出x, y的关系,结合圆的性质及几何意义可求答案。
8.【答案】B
【考点】向量的共线定理;向量的线性运算性质及几何意义
【解析】【解答】设,又因为,
设,则,则,解得,所以,
故答案为:B.
【分析】结合图形得性质以及平面向量的线性运算,求得与,然后根据 与 共线,得到方程组,解之即可.
9.【答案】B,C,D
【考点】向量的模;空间中的点的坐标
【解析】【解答】解:对A,,所以不成立,A不符合题意;
对于B,,
则,所以,B符合题意;
对于C,,C符合题意;
对于D,,则,D符合题意.
故答案为:BCD.
【分析】根据题意由空间数量积、向量模的坐标公式,代入数值计算出结果由此对选项逐一判断即可得出答案。
10.【答案】B,C
【考点】平行向量与共线向量;向量加减混合运算及其几何意义;向量的共线定理
【解析】【解答】对于A选项,由于向量不能比大小,A选项错误;
对于B选项, ,B选项正确;
对于C选项,已知向量 、 是非零向量, 、 的方向相同,C选项正确;
对于D选项,若 , ,则 ,但不存在实数 使得 ,D选项错误.
故答案为:BC.
【分析】由平面向量不能比较大小即可判断出选项A错误,由平面向量的加减法运算法则即可判断出选项B正确,由平面向量的线性运算即可判断出选项C正确,由特殊值法即可判断出选项D错误;由此即可得出答案。
11.【答案】A,B
【考点】平面向量数量积的坐标表示、模、夹角;数量积表示两个向量的夹角;异面直线及其所成的角;空间中直线与直线之间的位置关系
【解析】【解答】因为以顶点A为端点的三条棱长均为6,且它们彼此的夹角都是60°,
所以·=·=·=6×6×cos 60°=18,
(++)2=+++2·+2·+2·
=36+36+36+3×2×18=216,
则||=|++|=6, 所以A符合题意;
·=(++)·(-)
=·-·+-·+·- =0,所以B符合题意;
显然△AA1D 为等边三角形,则∠AA1D=60°.
因为=,且向量与的夹角是120°,所以与的夹角是120°,所以C不正确;
因为=+-=+ ,
所以||==6,||==6,
·=(+-)·(+)=36,
所以cos<>===,所以D不正确.
故答案为::AB.
【分析】以顶点A为端点的三条棱长均为6,且它们彼此的夹角都是60°,再利用数量积的定义得出·=·=·=18,再利用平行四边形法则和数量积求向量的模的公式,得出||的值;再利用数量积的运算法则结合数量积的定义,得出·=0,再利用数量积为0两向量垂直的等价关系,从而证出 AC1⊥DB ;再利用三角形△AA1D 为等边三角形,则∠AA1D=60°,再由=,且向量与的夹角是120°,从而求出与的夹角;再利用平面向量基本定理结合数量积求向量的模的公式,得出||和|的值,再利用数量积的运算法则求出数量积的值,再结合数量积求向量夹角公式,进而求出BD1与AC所成角的余弦值,从而找出说法正确的选项。
12.【答案】B,C
【考点】向量在几何中的应用
【解析】【解答】因为 与 共线,则 ,
所以
.
对于A,将 的图象向左平移 个单位得到函数
的图象,A不符合题意;
对于B, ,B符合题意;
对于C,当 时,则 ,
由余弦函数的对称轴为 ,C符合题意;
对于D, ,则 ,
由余弦函数的单调递增区间为 ,
当 时,余弦函数的单调递增区间为 ,
所以函数 在 上单调递增.
故答案为:BC
【分析】 根据向量共线建立方程关系,利用三角函数关系进行化简求出函数 的解析式,分别进行判断即可.
13.【答案】-4
【考点】平面向量共线(平行)的坐标表示
【解析】【解答】因为向量 ,且 与 共线,
所以 ,
解得: ,
故答案为:-4.
【分析】根据两个向量共线的性质,可得 ,解方程求得m的值。
14.【答案】
【考点】平面向量共线(平行)的坐标表示
【解析】【解答】因为 , ,所以 ,
因为 ,所以 ,解得 ,
故答案为: .
【分析】数学由向量的坐标公式求出,再由共线向量的坐标公式代入数值计算出结果即可。
15.【答案】
【考点】正弦定理;三角形中的几何计算
【解析】【解答】由已知和正弦定理得: ,
设 ,
由 ,
解得 ,所以 ,设 的外接圆的半径为 ,
由 ,解得 ,
由正弦定理得 ,所以 。
故答案为: 。
【分析】由已知和正弦定理得的比值,进而设 ,再利用已知的三角形面积公式,即 ,进而结合已知条件求出t的值,进而求出边长a,b,c的长,设 的外接圆的半径为 ,再利用三角形 的面积公式结合已知条件,进而求出角A的正弦值,再利用正弦定理的性质,进而求出三角形 的外接圆的半径。
16.【答案】1
【考点】余弦定理
【解析】【解答】画出过点 ,线段 的平面图如图所示:过点 作 于点 ,
因为 点是点 关于直线 对称点,所以 且 平分 ,
所以 ,
因为长方体 中, ,
所以 , , ,
所以 , ,所以
, ,
在 中由余弦定理得
,
故答案为:1
【分析】根据几何体画出平面图形,根据边长得出角的大小,转化到中, , ,根据条件运用余弦定理求解即可。
17.【答案】(1)由 ,根据正弦定理可得: ,则 ,
所以 ,
因为 ,所以 ,则 ;
(2)由(1)知 ,则 ,
所以 或 ,即 或 ,
因为 为三角形内角,所以 ;
因此 ,
所以 ,
因此 ,
所以 ,
又 ,根据正弦定理可得 ,则 ,
因此 的面积为 .
【考点】两角和与差的正弦公式;同角三角函数间的基本关系;正弦定理;余弦定理
【解析】【分析】(1)首先由正弦定理,以及两角和的正弦公式整理得到,由此得出
,从而求出角A的大小。
(2)由(1) 的结论以及角的取值范围,结合同角三角函数的基本关系时即可得出,再由两角和的正弦公式求出sinB的值,从而得出cosB的值,结合三角形的内角和性质以及两角和的正弦公式代入数值即可计算出sinC的值,然后由正弦定理计算出b的值,结合三角形的面积公式计算出结果即可。
18.【答案】(1)解:由正弦定理有, ,得
由余弦定理有
又由 ,可得
(2)解:由题意有
由正弦定理有 ,
由 ,有
由 ,有 ,可得
由正弦定理得
【考点】解三角形;正弦定理;余弦定理
【解析】【分析】(1)根据题意由正弦定理整理即可得出,然后由余弦定理代入数值计算出cosA的值,结合角的取值范围即可求出角A的大小。
(2)由已知条件结合正弦定理整理即可得到,结合题意即可求出,由此即可得出,结合正弦定理代入数值计算出结果即可。
19.【答案】(1)解:根据题意,,
两边平方得,即,
解得或(舍去),即.
(2)解:由余弦定理可得,所以,
由题意知,所以,所以.
根据正弦定理得,
因此
【考点】平面向量数量积的运算;正弦定理;余弦定理
【解析】【分析】(1)由 ,两边平方,解方程得出AB的值;
(2)由于弦定理得出AC,再由圆内接四边形的性质以及正弦定理得出.
20.【答案】解:
由 ,即
所以 ,由 ,则
所以 ,则
故 .
【考点】平面向量数量积的运算;正弦函数的单调性;诱导公式
【解析】【分析】 先用数量积公式得到f (x),化成辅助角形式,然后利用正弦函数的性质求出a,再由诱导公式计算求值即可.
21.【答案】(1)在 中, , , ,
由正弦定理可得 ,即 ,解得 ;
又A为钝角,所以 为锐角,则 ;
(2)由平面四边形 内接于一个圆可得 ,所以 ,
又A为钝角,所以 为锐角,则 ,
在 中,由余弦定理可得 ,
即 ,整理得 ,
解得 ,
则 的面积为 .
【考点】正弦定理;余弦定理
【解析】【分析】(1) 根据已知条件,在△ABD中,运用正弦定理,即可求解;
(2)根据已知条件,运用余弦定理,以及三角形面积公式,即可求解.
22.【答案】(1)解:因为 , ,
所以 ,
所以 , ,故 .
(2)解:∵ ,
∴ ,
∵ 为菱形,∴ ,
∴ ,即 .
【考点】向量的线性运算性质及几何意义;平面向量数量积的运算
【解析】【分析】 (1)结合向量线性运算的几何意义,用 表示出向量 ,即可求出x, y的值,进而求出 的值;
(2)将 用表示,结合已知求得 , ,然后结合数量积的定义求解即可求出 .
1 / 1
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
