北师大版八年级数学下册1.4.2 角平分线 教学设计
文档属性
| 名称 | 北师大版八年级数学下册1.4.2 角平分线 教学设计 |  | |
| 格式 | doc | ||
| 文件大小 | 480.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-18 16:33:17 | ||
图片预览

文档简介
第一章 三角形的证明
1.4.2 角平分线(二)
一、教学目标:
1.知识目标:
(1)引导学生发现并证明“三角形的三条角平分线相交于三角形內一点并且这一点到三边的距离相等”这一结论,即三角形中三条角平分线性质定理。
(2) 运用三角形中三条角平分线性质定理解决问题。
(3)角平分线的性质定理和判定定理的综合运用.
2.能力目标:
(1)进一步发展学生的推理证明意识和能力.
(2)培养学生将文字语言转化为符号语言、图形语言的能力.
(3)提高综合运用数学知识和方法解决问题的能力.
3.情感与价值观要求
(1)能积极参与数学学习活动,对数学有好奇心和求知欲.
(2)在数学活动中获得成功的体验,锻炼克服困难的意志,建立自信心.
二、教学重点、难点
重点:(1)三角形三个内角的平分线的性质.
(2)综合运用角平分线的性质和判定定理,解决几何中的问题.
难点:角平分线的性质定理和判定定理的综合应用.
三、教学过程
1.创设问题情境,引入新课。
三条公路围成了一个三角形区域, 要在这个
三角形区域内建一果品批发市场到这三条公路的距
离相等,试找出批发市场的位置.
2.复习回顾:
(1)角平分线的性质定理?
(2)角平分线的判定定理?
(3)遇到角平分线上的点如何添加辅助线?
3. 新知探究
【活动一】
利用自己准备好的三角形纸片,通过折叠找出每个角的角平分线,观察这三条角平分线,你发现了什么?与同伴交流。
师引导学生归纳:三条角平分线相交于三角形内一点。
【活动二】
作三角形三个内角的角平分线,你又发现了什么?
(放映尺规作图视频)
师引导学生归纳:三条角平分线相交于三角形内一点。
思考:仅凭观察和猜想得到的结论可靠吗?
我们利用折纸和尺规作图的方法都发现三角形的三条角平分线相交于一点,并且这一点到三条边的距离相等。你能证明这个结论吗?
例2求证:三角形的三条角平分线相交于一点,并且这一点到三角形三条边的距离相等。
引导学生把文字语言转换成图形和几何语言如下:
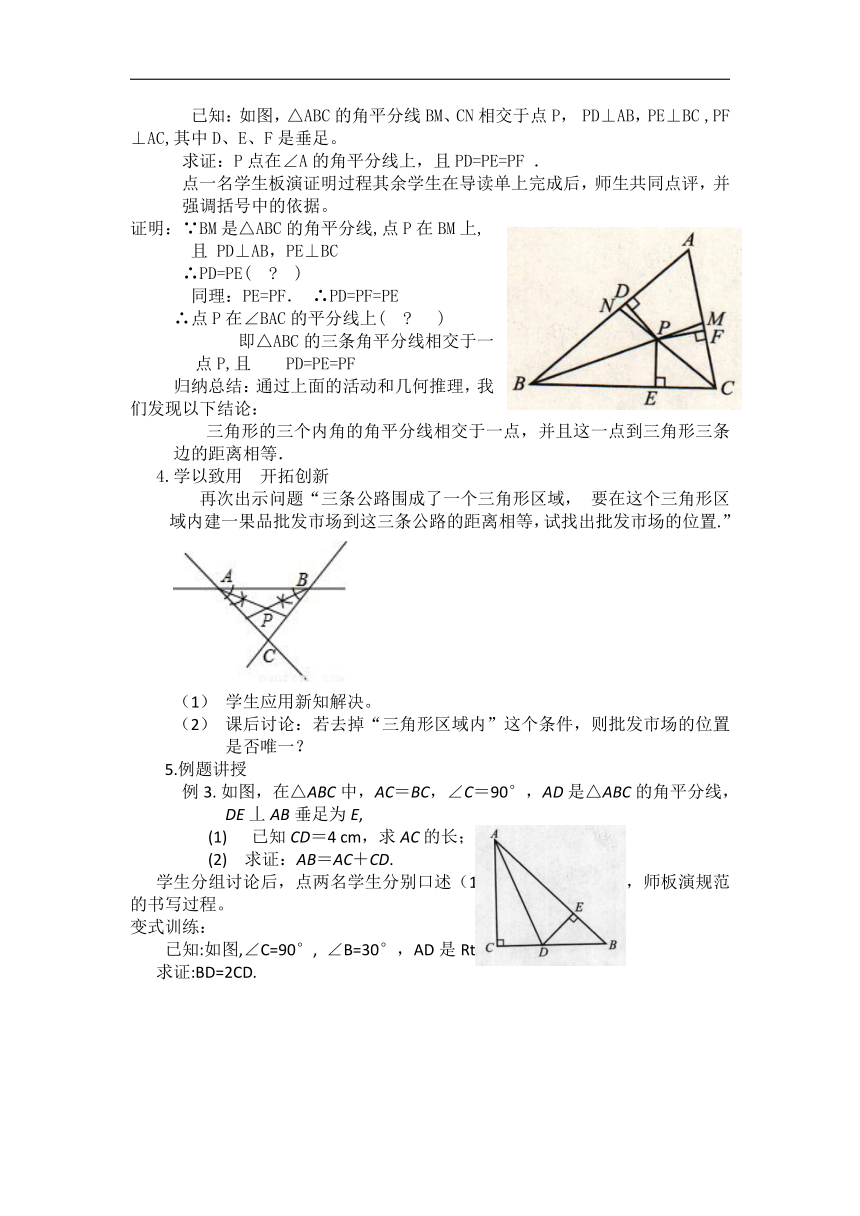
已知:如图,△ABC的角平分线BM、CN相交于点P, PD⊥AB,PE⊥BC ,PF⊥AC,其中D、E、F是垂足。
求证:P点在∠A的角平分线上,且PD=PE=PF .
点一名学生板演证明过程其余学生在导读单上完成后,师生共同点评,并强调括号中的依据。
证明:∵BM是△ABC的角平分线,点P在BM上,
且 PD⊥AB,PE⊥BC
∴PD=PE( )
同理:PE=PF. ∴PD=PF=PE
∴点P在∠BAC的平分线上( )
即△ABC的三条角平分线相交于一点P,且 PD=PE=PF
归纳总结:通过上面的活动和几何推理,我们发现以下结论:
三角形的三个内角的角平分线相交于一点,并且这一点到三角形三条边的距离相等.
4.学以致用 开拓创新
再次出示问题“三条公路围成了一个三角形区域, 要在这个三角形区域内建一果品批发市场到这三条公路的距离相等,试找出批发市场的位置.”
(1) 学生应用新知解决。
(2) 课后讨论:若去掉“三角形区域内”这个条件,则批发市场的位置是否唯一?
5.例题讲授
例3. 如图,在△ABC中,AC=BC,∠C=90°,AD是△ABC的角平分线,DE丄AB垂足为E,
(1) 已知CD=4 cm,求AC的长;
(2) 求证:AB=AC+CD.
学生分组讨论后,点两名学生分别口述(1)、(2)的解题过程,师板演规范的书写过程。
变式训练:
已知:如图,∠C=90°, ∠B=30°,AD是Rt△ABC的角平分线.
求证:BD=2CD.
学生分组讨论后,师点一名学生上讲台讲解解题过程。然后提问全体学生解题过程中重要的知识点?使学生透彻理解该题。
通过例3和变式训练引导学生归纳小结:
角平分线的性质是证明边相等的重要依据,常与直角三角形的性质、勾股理及其逆定理等综合应用,在应用中常用到“构造法”和“转化思想”.
6.随堂练习:
已知:如图,在Rt△ABC中,∠ACB=90°, ∠B=60°,AD,CE是角平分线,AD与CE相交于点F,FM⊥AB,FN⊥BC,垂足分别为 M,N.
求证:FE=FD.
学生分组讨论后,师请学生代表上台讲解题思路及过程。
师利用课件展示规范的解题的过程。
7.课堂小结,畅谈收获?
(1)学习并证明了定理“三角形三条角平分线相交于一点,且这一点到三角形三边的距离相等。
(2)应用角平分线相关定理解决几何当中的计算和证明问题。
(3)转化思想和构造法的具体应用。
8.作业布置
课后作业:习题1.10第1、2、3题
四、教学反思
本节课我设计的教学思路是按“操作、猜想、验证、运用”的学习过程,遵循学生的认知规律,先学习新知:三角形中角平分线的性质定理,再结合第一课时角平分线性质定理和判定定理来进一步提高学生的思维水平和应用数学知识解决实际问题的能力。
上完这节课后,感觉和预期的效果还是比较接近,学生在课堂上也积极参与思考、大胆尝试、主动探讨、勇于创新。在此教学中,只需真正实施民主的开放式教学,创设平等、民主、宽松的教学氛围,使师生完全处于平等的地位,学生才能敞开思想,积极参与教学活动,才能最大限度地调动学生的积极性,激发他们的学习兴趣,引导他们多角度、多方位、多层次地思考问题,使他们有足够的机会显示灵性,展现个性。让学生自主参与学习,解决问题,体验到参与的乐趣、合作的价值,并获得成功的体验。我回想这节课,还有以下三点需要注意:
1.对课堂所用时间分配不够准确。例如在讲完三角形三条角平分线性质定理后应再设计一道应用定理的练习题会更好,还有后面的例题和变式训练留给学生讨论的时间不够充分。
2.提问要注意精心设计,语言要简练,易懂。
3.角平分线的判定定理应用题目设计较少,应在课后再加强训练。
针对以上的不足,我在今后的教学中会加以改进,使教学的实效性得到最大限度提升。
A
B
C
D
1.4.2 角平分线(二)
一、教学目标:
1.知识目标:
(1)引导学生发现并证明“三角形的三条角平分线相交于三角形內一点并且这一点到三边的距离相等”这一结论,即三角形中三条角平分线性质定理。
(2) 运用三角形中三条角平分线性质定理解决问题。
(3)角平分线的性质定理和判定定理的综合运用.
2.能力目标:
(1)进一步发展学生的推理证明意识和能力.
(2)培养学生将文字语言转化为符号语言、图形语言的能力.
(3)提高综合运用数学知识和方法解决问题的能力.
3.情感与价值观要求
(1)能积极参与数学学习活动,对数学有好奇心和求知欲.
(2)在数学活动中获得成功的体验,锻炼克服困难的意志,建立自信心.
二、教学重点、难点
重点:(1)三角形三个内角的平分线的性质.
(2)综合运用角平分线的性质和判定定理,解决几何中的问题.
难点:角平分线的性质定理和判定定理的综合应用.
三、教学过程
1.创设问题情境,引入新课。
三条公路围成了一个三角形区域, 要在这个
三角形区域内建一果品批发市场到这三条公路的距
离相等,试找出批发市场的位置.
2.复习回顾:
(1)角平分线的性质定理?
(2)角平分线的判定定理?
(3)遇到角平分线上的点如何添加辅助线?
3. 新知探究
【活动一】
利用自己准备好的三角形纸片,通过折叠找出每个角的角平分线,观察这三条角平分线,你发现了什么?与同伴交流。
师引导学生归纳:三条角平分线相交于三角形内一点。
【活动二】
作三角形三个内角的角平分线,你又发现了什么?
(放映尺规作图视频)
师引导学生归纳:三条角平分线相交于三角形内一点。
思考:仅凭观察和猜想得到的结论可靠吗?
我们利用折纸和尺规作图的方法都发现三角形的三条角平分线相交于一点,并且这一点到三条边的距离相等。你能证明这个结论吗?
例2求证:三角形的三条角平分线相交于一点,并且这一点到三角形三条边的距离相等。
引导学生把文字语言转换成图形和几何语言如下:
已知:如图,△ABC的角平分线BM、CN相交于点P, PD⊥AB,PE⊥BC ,PF⊥AC,其中D、E、F是垂足。
求证:P点在∠A的角平分线上,且PD=PE=PF .
点一名学生板演证明过程其余学生在导读单上完成后,师生共同点评,并强调括号中的依据。
证明:∵BM是△ABC的角平分线,点P在BM上,
且 PD⊥AB,PE⊥BC
∴PD=PE( )
同理:PE=PF. ∴PD=PF=PE
∴点P在∠BAC的平分线上( )
即△ABC的三条角平分线相交于一点P,且 PD=PE=PF
归纳总结:通过上面的活动和几何推理,我们发现以下结论:
三角形的三个内角的角平分线相交于一点,并且这一点到三角形三条边的距离相等.
4.学以致用 开拓创新
再次出示问题“三条公路围成了一个三角形区域, 要在这个三角形区域内建一果品批发市场到这三条公路的距离相等,试找出批发市场的位置.”
(1) 学生应用新知解决。
(2) 课后讨论:若去掉“三角形区域内”这个条件,则批发市场的位置是否唯一?
5.例题讲授
例3. 如图,在△ABC中,AC=BC,∠C=90°,AD是△ABC的角平分线,DE丄AB垂足为E,
(1) 已知CD=4 cm,求AC的长;
(2) 求证:AB=AC+CD.
学生分组讨论后,点两名学生分别口述(1)、(2)的解题过程,师板演规范的书写过程。
变式训练:
已知:如图,∠C=90°, ∠B=30°,AD是Rt△ABC的角平分线.
求证:BD=2CD.
学生分组讨论后,师点一名学生上讲台讲解解题过程。然后提问全体学生解题过程中重要的知识点?使学生透彻理解该题。
通过例3和变式训练引导学生归纳小结:
角平分线的性质是证明边相等的重要依据,常与直角三角形的性质、勾股理及其逆定理等综合应用,在应用中常用到“构造法”和“转化思想”.
6.随堂练习:
已知:如图,在Rt△ABC中,∠ACB=90°, ∠B=60°,AD,CE是角平分线,AD与CE相交于点F,FM⊥AB,FN⊥BC,垂足分别为 M,N.
求证:FE=FD.
学生分组讨论后,师请学生代表上台讲解题思路及过程。
师利用课件展示规范的解题的过程。
7.课堂小结,畅谈收获?
(1)学习并证明了定理“三角形三条角平分线相交于一点,且这一点到三角形三边的距离相等。
(2)应用角平分线相关定理解决几何当中的计算和证明问题。
(3)转化思想和构造法的具体应用。
8.作业布置
课后作业:习题1.10第1、2、3题
四、教学反思
本节课我设计的教学思路是按“操作、猜想、验证、运用”的学习过程,遵循学生的认知规律,先学习新知:三角形中角平分线的性质定理,再结合第一课时角平分线性质定理和判定定理来进一步提高学生的思维水平和应用数学知识解决实际问题的能力。
上完这节课后,感觉和预期的效果还是比较接近,学生在课堂上也积极参与思考、大胆尝试、主动探讨、勇于创新。在此教学中,只需真正实施民主的开放式教学,创设平等、民主、宽松的教学氛围,使师生完全处于平等的地位,学生才能敞开思想,积极参与教学活动,才能最大限度地调动学生的积极性,激发他们的学习兴趣,引导他们多角度、多方位、多层次地思考问题,使他们有足够的机会显示灵性,展现个性。让学生自主参与学习,解决问题,体验到参与的乐趣、合作的价值,并获得成功的体验。我回想这节课,还有以下三点需要注意:
1.对课堂所用时间分配不够准确。例如在讲完三角形三条角平分线性质定理后应再设计一道应用定理的练习题会更好,还有后面的例题和变式训练留给学生讨论的时间不够充分。
2.提问要注意精心设计,语言要简练,易懂。
3.角平分线的判定定理应用题目设计较少,应在课后再加强训练。
针对以上的不足,我在今后的教学中会加以改进,使教学的实效性得到最大限度提升。
A
B
C
D
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
