精讲精练·专项突破 第一章《空间向量与几何》单元能力提升(含详细解析) (2)
文档属性
| 名称 | 精讲精练·专项突破 第一章《空间向量与几何》单元能力提升(含详细解析) (2) |  | |
| 格式 | docx | ||
| 文件大小 | 335.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-18 16:27:47 | ||
图片预览




文档简介
精讲精练·专项突破
2021-2022学年高二上学期人教版(2019)
第一章 《空间向量与几何》 单元能力提升(含详细解析)
一、单选题
1.(2021高二上·安徽月考)已知平面 内有一点 ,平面 的一个法向量 ,则下列各点在平面 内的是( )
A. B. C. D.
【答案】D
【考点】数量积的坐标表达式;空间中的点的坐标;平面的法向量
【解析】【解答】解:设点 在平面 内, ,因为平面 的一个法向量 ,所以 ,即 ,满足该条件的只有D选项.
故答案为:D.
【分析】首先由点的坐标求出向量的坐标,再由平面法向量的定义求出平面 的法向量,然后由数量积的坐标公式代入计算出结果由此得到答案。
2.(2021高一下·重庆期末)在正方体ABCD-A1B1C1D1中,E是C1D1的中点,则异面直线DE与AC所成角的余弦值为( )
A. B. C. D.
【答案】B
【考点】用空间向量求直线间的夹角、距离
【解析】【解答】设正方体棱长为1,以D为原点建立空间直角坐标系如图所示,
则D(0,0,0),E(0, ,1),A(1,0,0),C(0,1,0),
所以 =(0, ,1), =(-1,1,0),
则 ,
则异面直线DE与AC所成角的余弦值为 .
故答案为:B.
【分析】以D为原点建立空间直角坐标系如图所示,利用向量法求出异面直线DE与AC所成角的余弦值 。
3.(2021高二上·砀山月考)在空间直角坐标 中, 为坐标原点,若点 在平面 上的投影点为B,则线段OB的长度为( )
A. B. C. D.3
【答案】A
【考点】点、线、面间的距离计算
【解析】【解答】解:∵点B是点 在平面 上的投影点
∴点B为(1,0,2)
∴
故答案为:A
【分析】根据空间中两点距离公式求解即可.
4.(2021高二上·葫芦岛月考)若空间向量 , ,则 ( )
A. B.3 C. D.
【答案】D
【考点】空间向量的加减法;空间向量运算的坐标表示
【解析】【解答】解: ,
.
故答案为:D
【分析】利用已知条件结合向量加法坐标运算和向量模长的坐标表示,可以算出模长.
5.(2021高二上·浙江期中)如图,在直三棱柱 中, , 分别是棱 的中点,则异面直线 与 所成角的大小为( )
A.30° B.45° C.60° D.90°
【答案】B
【考点】用空间向量求直线间的夹角、距离
【解析】【解答】由题意以 为 轴建立空间直角坐标系,如图,
则 , . , , ,
, ,
,
所以 ,即异面直线 与 所成角是45 .
故答案为:B.
【分析】以 为 轴建立空间直角坐标系,用向量法求异面直线所成的角。
6.(2021高二上·沈阳期中)如图,在棱长为2的正方体ABCD A1B1C1D1中,E为BC的中点,点P在线段D1E上,点P到直线CC1的距离的最小值为( )
A. B. C. D.
【答案】A
【考点】点、线、面间的距离计算
【解析】【解答】以D为原点, 分别为x轴、y轴、z轴建立空间直角坐标系,
则E(1,2,0),D1(0,0,2), , ,
, , ,
设 (x,y,z), , ,
则 (x,y,z)·(0,0,2)=0,∴z=0,
=(x,y,z)·(-1,-2,2)= ,∴y=- x,
令x=1,则y=- ,∴u=(1,- ,0),
∴异面直线D1E与CC1的距离为d= ,
∵P在D1E上运动,∴P到直线CC1的距离的最小值为d= .
故答案为:A.
【分析】以D为原点, 分别为x轴、y轴、z轴建立空间直角坐标系,求出对应点的坐标,再利用平面向量数量积的运算可得y=- x,令x=1,则y=- ,利用向量表示出异面直线D1E与CC1的距离,可得答案。
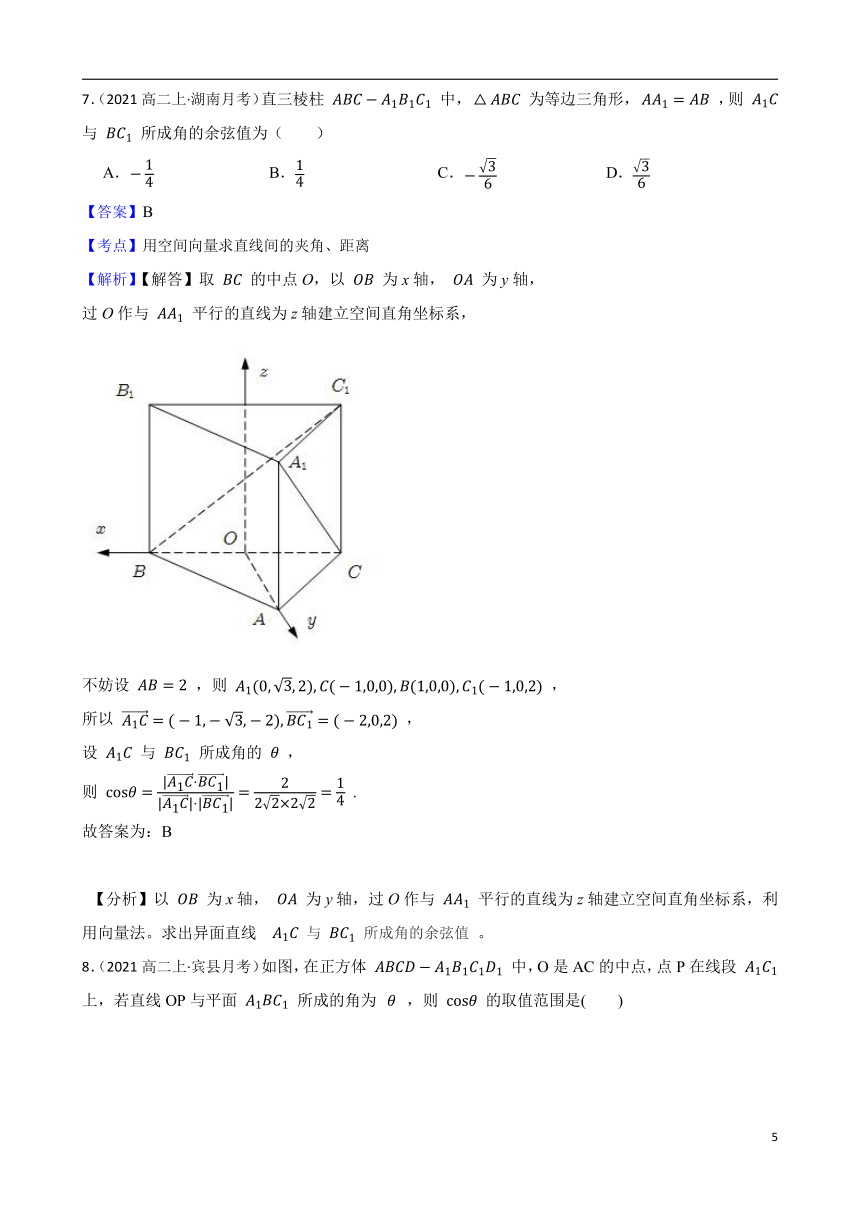
7.(2021高二上·湖南月考)直三棱柱 中, 为等边三角形, ,则 与 所成角的余弦值为( )
A. B. C. D.
【答案】B
【考点】用空间向量求直线间的夹角、距离
【解析】【解答】取 的中点O,以 为x轴, 为y轴,
过O作与 平行的直线为z轴建立空间直角坐标系,
不妨设 ,则 ,
所以 ,
设 与 所成角的 ,
则 .
故答案为:B
【分析】以 为x轴, 为y轴,过O作与 平行的直线为z轴建立空间直角坐标系,利用向量法。求出异面直线 与 所成角的余弦值 。
8.(2021高二上·宾县月考)如图,在正方体 中,O是AC的中点,点P在线段 上,若直线OP与平面 所成的角为 ,则 的取值范围是( )
A. B. C. D.
【答案】B
【考点】用空间向量求直线与平面的夹角;同角三角函数间的基本关系
【解析】【解答】解:设正方体边长为2,建立如图所示空间直角坐标系,
则O(1,1,0),A1(2,0,2),B(2,2,0),C1(0,2,2),
设P(a,2-a,2)(0≤a≤2),则,
由于使,,
所以是平面A1BC1的法向量,
所以
∵0≤a≤2
∴,
∴,
∴,
∴,
∴,
又∵,
∴,
故答案为:B
【分析】先利用向量法求得直线OP与平面 所成的角的正弦值sinθ,再根据同角三角函数间的基本关系求解即可.
二、多选题
9.设 , 为空间中的任意两个非零向量,下列各式中正确的有( ).
A.
B.
C.
D.
【答案】A,D
【考点】空间向量的数量积运算
【解析】【解答】由数量积的性质和运算律可知AD是正确的;
而 运算后是实数, 没有这种运算,B不正确;
,C不正确.
故答案为:AD.
【分析】根据题意由数量积的运算性质以及向量的运算性质对选项逐一判断即可得出答案。
10.(2021高二上·大连期中)已知正方体的棱长为,点,分别是,的中点,在正方体内部且满足,则下列说法正确的是( )
A.直线平面
B.直线与平面所成的角为
C.直线与平面的距离为
D.点到直线的距离为
【答案】A,B,D
【考点】直线与平面平行的性质;直线与平面垂直的性质;空间向量的夹角与距离求解公式;用空间向量求直线与平面的夹角;用空间向量求平面间的夹角
【解析】【解答】平面,平面,,,,故平面,平面,故,同理可得,,故直线平面,A符合题意;
如图所示:连接 与 交于点 ,则 , , ,
故 平面 ,即 为直线 与平面 所成的角, ,B符合题意;
, 平面 ,故 平面 , 为 中点,连接 ,则 ,故 平面 , ,C不符合题意;
以 为 轴建立空间直角坐标系,
则 , ,
,点 到直线 的距离为 ,D符合题意.
故答案为:ABD.
【分析由线面垂直的性质定理和判定定理,结合正方体的几何性质即可判断出选项A正确;根据题意作出辅助线,由正方体的几何性质结合线面角的定义即可得出 为直线与平面所成的角,然后由三角形中的几何计算关系即可求出结果,由此判断出选项B正确;根据题意由线面平行的判定定理结合正方体的几何性质即可得出平面,然后由题意作出辅助线,结合中点的坐标以及点到直线的距离公式计算出结果,由此判断出选项C错误;根据题意建立空间直角坐标系求出各个点的坐标以及向量的坐标,再由空间向量的距离公式代入数值计算出结果,由此判断出选项D正确,从而得出答案。
11.(2022高三上·河北月考)如图,在正方体中,分别为的中点,则下列说法正确的是( )
A. B.平面
C.与所成的角的余弦值为 D.点到平面的距离为
【答案】A,D
【考点】异面直线及其所成的角;直线与平面平行的判定;直线与平面垂直的性质;点、线、面间的距离计算
【解析】【解答】A选项:取中点为,则易得:,故与,,可得平面,又平面,故,A符合题意;
B选项:若平面,则平面或在平面内,显然不成立,B不符合题意;
C选项:取中点为,则即为所求角,,故,D不符合题意;
D选项:三棱锥中,,
等边三角形的外接圆半径为,
所以到平面的距离为,D符合题意.
故答案为:AD
【分析】根据题意由正方体的几何性质以及线面垂直的性质定理即可得出线线垂直,由此判断出选项A正确;由线面平行的性质定理结合正方体的几何性质即可判断出选项B错误;由正方体的几何性质即可得出即为所求角,结合三角形中的几何计算关系计算出结果即可,由此判断出选项C错误;由三棱锥的几何性质即可求出边的大小,再由外接圆的几何性质计算出圆的半径,然后由点到平面的距离公式,代入数值计算出结果,由此即可判断出选项D正确,由此即可得出答案。
12.(2021·汕头模拟)正方体 ,的棱长为4,已知 平面α, ,则关于α β截此正方体所得截面的判断正确的是( )
A.α截得的截面形状可能为正三角形
B. 与截面α所成角的余弦值为
C.α截得的截面形状可能为正六边形
D.β截得的截面形状可能为正方形
【答案】A,B,C
【考点】用空间向量求直线与平面的夹角
【解析】【解答】解:A选项:为正三角形的情况为△B1CD1,故A正确;
B选项:不妨设截面a是△B1CD1,由于直线与平面所成角的余弦值等于直线与平面法向量所成角正弦值,且AC1为平面B1CD1的法向量,则∠A1AC1即为直线与法向量为夹角,
设夹角为θ,则其正弦值为,故B正确;
C选项:为正六边形的情况为A1D1,A1B1,B1B,BC,CD,D1D中点连线构成,故C正确;
D选项:由于直线AC1为体对角线,且,在正方体上任找一点(排除A1C1)与A1C1可构成平面β,但无法得到正方形截面,故D错误.
故答案为:ABC
【分析】根据正方体的几何特征,利用向量法求直线与平面所成的角,结合正三角形及正六边形的几何特征求解即可.
三、填空题
13.(2021高二上·玉溪月考) 是半径为2的球O表面上三个点, 的外接圆面积为 ,则球心O 到平面 的距离为
【答案】
【考点】点、线、面间的距离计算
【解析】【解答】解:由题意设球的半径为R, 的外接圆半径为r,
则由πr2=π,得r=1,
则球心O到平面 的距离为
故答案为:
【分析】根据圆的面积公式,结合点到平面的距离求解即可.
14.(2020高二上·蚌埠期末)正方体 中,点P是 的中点,则异面直线AP与 所成角的大小为 .
【答案】
【考点】异面直线及其所成的角;用空间向量求直线与平面的夹角
【解析】【解答】设正方体 的棱长为2,连接
在正方体 中,
所以 (或其补角)为异面直线AP与 所成角
所以
所以
故答案为:
【分析】首先根据题意由正方体的性质即可求出异面直线所成的角,再由夹角的数量积公式代入数值计算出夹角的余弦值,从而即可求出角的大小。
15.(2021高三上·南京月考)在三棱锥 中, 和 都是边长为 的正三角形, .若 为三棱锥 外接球上的动点,则点 到平面 距离的最大值为 .
【答案】
【考点】球的体积和表面积;球内接多面体;点、线、面间的距离计算
【解析】【解答】设 中点为 , 的外心为 , 的外心为 ,
过点 作面 的垂线,过点 作直线面 的垂线,
两条垂线的交点 即为三棱锥 外接球的球心,
因为 和 都是边长为 的正三角形,可得 ,
又 ,所以 ,所以 ,
又因为 , ,所以 面 ,
因为 平面 ,所以平面 平面 ,且 ,
所以四边形 是边长为1的正方形,所以外接球半径 ,
到平面 的距离 ,
故答案为: .
【分析】根据题意做出辅助线,由已知条件即可得出两条垂线的交点 即为三棱锥 外接球的球心,结合三棱锥的几何性质由勾股定理计算出线线垂直,然后由线面垂直的判定定理即可得证出 面 ,从而得到平面 平面 由此计算出外接球的半径值,从而得出答案。
16.(2021高二上·茂名期中)下列关于空间向量的命题中,
①若向量 , 与空间任意向量都不能构成基底,则 ;
②若非零向量 , , 满足 , ,则有 ;
③若 , , 是空间的一组基底,且 ,则 , , , 四点共面;
④若向量 , , ,是空间一组基底,则 , , 也是空间的一组基底.
上述命题中,正确的有 .
【答案】①③④
【考点】空间向量的基本定理及其意义
【解析】【解答】解:对于①, 若向量 , 与空间任意向量都不能构成基底,则向量 , 与空间任意向量都共面,则与必共线,即//,故①正确;
对于②, 若非零向量 , , 满足 , ,当非零向量 , , 不共面时, 与可以不平行,故②不正确;
对于③,因为 ,所以,
所以,所以共面,所以 , , , 四点共面,故③正确;
对于④,若向量 , ,是空间一组基底,则向量 , , 不共面,则对任意实数x,y都有,即,
所以 , , 不共面,所以 , , 也是空间的一组基底.故④正确.
故答案为:①③④
【分析】根据空间向量基本定理可知,能作为基底的向量一定是不共面的向量,由此对四个命题逐个分析可得答案.
四、解答题
17.(2021高二下·思明期中)如图,四边形 为正方形, 平面 ,点 分别为 的中点,且 , .
(1)证明: 平面 ;
(2)求二面角 的大小.
【答案】(1)解:证明:取 的中点为 ,连接
又 为 的中点,所以 ,且 ,
因为 ,且 ,
所以 ,且 ,
故四边形 为平行四边形,则
又 平面 , 平面 ,
所以 平面 ,
(2)因为 , , 平面 ,所以
而四边形 为正方形,所以可如图建立空间直角坐标系
, , ,
所以 , ,
设平面 的一个法向量为 ,则
∴ ,
同理可得平面 的一个法向量为
所以 ,
由图知二面角 为钝角,则大小为 .
【考点】直线与平面平行的判定;用空间向量求平面间的夹角
【解析】【分析】(1) 取 的中点为 ,连接 ,又因为 为 的中点,再利用中点作中位线的方法结合中位线的性质,所以 且 ,因为 且 ,
所以 且 ,故四边形 为平行四边形,则 ,再利用线线平行证出线面平行,从而证出直线 平面 。
(2) 因为 , , 平面 ,所以 ,而四边形 为正方形,所以可建立空间直角坐标系 ,从而求出点的坐标,再利用向量的坐标表示求出向量的坐标,再结合数量积求向量夹角公式,从而求出二面角 的大小。
18.(2021·绵阳模拟)如图,在四棱锥 中,四边形 为梯形, , , 平面 .
(1)求证:平面 平面 ;
(2)若 , ,求二面角 所成角的余弦值.
【答案】(1)证明:由 平面 ,且 平面 ,所以 .
又由 ,且 ,所以 平面 .
因为 平面 ,所以平面 平面 .
(2)解:建立如图所示空间直角坐标系 ,
因为 平面 , 平面 ,所以 .
由 , ,可得 , , ,
则 ,
设平面 的法向量为 ,
则 ,即得 ,取 ,得 , ,
所以平面 的一个法向量为 .
取平面 的一个法向量 ,
可得 .
因为二面角 所成角为锐角,所以二面角 的余弦值为 .
【考点】平面与平面垂直的判定;用空间向量求平面间的夹角
【解析】【分析】 (1)利用线面垂直的性质定理即可得出线线垂直,再结合线面垂直的判定定理即可得证出结论。
(2)建立合适的空间直角坐标系,求出所需点的坐标和向量的坐标,然后利用待定系数法求出平面的法向量,由向量的夹角公式求解即可.
19.(2022·邵阳模拟)如图,四棱锥A-BCDE的底面为等腰梯形,,且,,平面平面ACB.
(1)证明:.
(2)若,求二面角C-AD-E的大小.
【答案】(1)证明:因为平面平面ACB,且平面平面,
,平面ACB,所以平面ACD.
又因为平面ACD,所以.
(2)解:分别以 为轴,过点作平面的垂线为轴,如图,建立空间直角坐标系,连接BD.
由已知条件,易得,,.
在△BCD中,由余弦定理可得,所以.
在△ACD中,由余弦定理得,所以.
因为,所以,,
设为平面ADE的法向量,
由 ,得,取,则.
又平面ACD的一个法向量为.
所以.
又面角C-AD-E为钝角,所以二面角C-AD-E为.
【考点】数量积表示两个向量的夹角;直线与平面垂直的性质;平面与平面垂直的性质;用空间向量求平面间的夹角;余弦定理
【解析】【分析】(1)根据题意由面面垂直的性质定理即可得出线面垂直,再由线面垂直的性质定理即可得出线线垂直。
(2) 根据题意建立空间直角坐标系,由此求出点以及向量的坐标,然后由数量积的坐标公式计算出平面的法向量,再由向量夹角公式结合余弦定理代入数值计算出结果即可。
20.(2020高三上·泰安期末)如图,在四棱锥 中,底面 是菱形, , , 为 上一点,过 作与 平行的平面 ,分别交 , 于点 , .
(1)证明: 平面 ;
(2)若 为 的中点, ,直线 与平面 所成角为60°.求平面 与平面 所成锐二面角的余弦值.
【答案】(1)证明:连接 ,交 于点 ,连接 .
∵ 平面 ,平面 平面 , 平面 ,∴ .
∵底面 是菱形,∴ ,且 为 , 中点,
又 ,∴ ,又 , 平面 ,
∴ 平面 ,∴ 平面 .
(2)解:∵ ,∴ ,由(1)知 , , 平面 ,
∴ 平面 ,∴ .
∵ ,∴ , ,又 , ,∴ .
以 为原点, , , 所在直线分别为 轴, 轴, 轴,建立如图所示的空间直角坐标系,
则 , , , , ,
∴ , , , , ,
设平面 的一个法向量为 ,则 ,∴ .
令 ,解得 ,∴ .
设平面 的一个法向量为 ,则 ,
∴ .
令 ,解得 ,∴ ,
∴ , , .
∴ .
∴平面 与平面 所成锐二面角的余弦值为 .
【考点】直线与平面垂直的判定;直线与平面垂直的性质;空间向量的数量积运算;用空间向量求平面间的夹角
【解析】【分析】(1)根据题意作出辅助线再由线面平行的性质定理即可得出线线平行,结合菱形的性质以及中点的性质即可得出线线垂直,然后由线面垂直的判定定理即可得证出结论。
(2)由已知条件结合由(1)的结论即可得出线面垂直由此得出线线垂直,由此建立空间直角坐标系求出各个点的坐标以及向量的坐标,再由数量积的坐标公式即可求出平面的法向量的坐标,同理即可求出平面的法向量;结合空间数量积的运算公式代入数值即可求出夹角的余弦值,由此得到 平面 与平面 所成锐二面角的余弦值 。
21.(2021·商丘模拟)如图,在三棱锥 中,平面 平面 , , , , .
(1)证明: ;
(2)若 ,求二面角 的余弦值.
【答案】(1) , , ,
又平面 平面 , 平面 ,
.
, ,
又 , 平面 ,
又 平面 ,
.
(2)如图,分别以 , 所在直线为 轴, 轴,过 垂直于平面 的直线为 轴,建立空间直角坐标系.
则 , , , , .
, , ,
设 为平面 的法向量,
则 则可取 ,
设 为平面 的法向量,
则 则可取 ,
则 .
结合图形可知,二面角 的余弦值为 .
【考点】直线与平面垂直的判定;直线与平面垂直的性质;空间向量的数量积运算;用空间向量求平面间的夹角
【解析】【分析】(1)根据题意由等边三角形的几何关系即可得出线线垂直,再由线面垂直的判定定理和性质定理即可得出 平面 以及 ,结合勾股定理计算出垂直关系,再由线面垂直的判定定理即可得出 平面 ,由线面垂直的性质定理即可证出结论 。
(2)由(1)的结论即可得出线线垂直由此 分别以 , 所在直线为 轴, 轴,过 垂直于平面 的直线为 轴,建立空间直角坐标系,求出各个点的坐标以及向量和平面法向量的坐标,再由数量积的坐标公式即可求出平面的法向量的坐标,同理即可求出平面的法向量;结合空间数量积的运算公式代入数值即可求出夹角的余弦值,由此得到 二面角 的余弦值.
22.(2021高二上·六安开学考)如图所示,多面体ABCDEF中, 平面ABCD,四边形ABCD是菱形, , ,四边形BDEF是正方形.
(1)求证: 平面AED;
(2)求直线AF与平面ECF所成角的正弦值;
(3)在线段EC上是否存在点P,使得 平面CEF?若存在,求出 的值;若不存在,请说明理由.
【答案】(1)解:因为四边形ABCD是菱形,所以 .
又 平面ADE, 平面ADE,
所以 平面ADE,
又四边形BDEF是正方形,所以 .
因为 平面ADE, 平面ADE,
所以 平面ADE,
因为 平面BCF, 平面BCF, ,
所以平面 平面AED,
因为 平面BCF,所以 平面AED.
(2)因为四边形ABCD为菱形,且 ,
所以 为等边三角形,取BD的中点O,连接CO,所以 ,
取EF的中点G,连接OG,则 ,
因为 平面ABCD,所以 平面ABCD,
故可建立如图所示的空间直角坐标系 .
则 , , , , , ,
所以 , , .
设平面ECF的法向量为 ,
则有 ,得 ,
,令 ,则 .
设直线AF与平面ECF所成的角为 ,
则 ,
所以直线AF与平面ECF所成角的正弦值为 .
(3)不存在.理由如下:
由(2)得 , ,
设 , ,
由 ,
得 ,
由(2)得平面CEP的一个法向量为 .
若 平面CEF,则 ,令 ,
得 ,
方程组无解,不符合题意.
综上,线段EC上不存在点P,使得 平面CEF.
【考点】直线与平面平行的判定;平面与平面平行的判定;向量语言表述线面的垂直、平行关系;用空间向量求直线与平面的夹角
【解析】【分析】(1)根据直线与平面平行的判定定理,以及平面与平面平行的判定定理求证即可;
(2)建立恰当的空间直角坐标系,利用向量法直接求解即可;
(3)根据向量的坐标运算,结合向量法直接求解即可.
23
2021-2022学年高二上学期人教版(2019)
第一章 《空间向量与几何》 单元能力提升(含详细解析)
一、单选题
1.(2021高二上·安徽月考)已知平面 内有一点 ,平面 的一个法向量 ,则下列各点在平面 内的是( )
A. B. C. D.
【答案】D
【考点】数量积的坐标表达式;空间中的点的坐标;平面的法向量
【解析】【解答】解:设点 在平面 内, ,因为平面 的一个法向量 ,所以 ,即 ,满足该条件的只有D选项.
故答案为:D.
【分析】首先由点的坐标求出向量的坐标,再由平面法向量的定义求出平面 的法向量,然后由数量积的坐标公式代入计算出结果由此得到答案。
2.(2021高一下·重庆期末)在正方体ABCD-A1B1C1D1中,E是C1D1的中点,则异面直线DE与AC所成角的余弦值为( )
A. B. C. D.
【答案】B
【考点】用空间向量求直线间的夹角、距离
【解析】【解答】设正方体棱长为1,以D为原点建立空间直角坐标系如图所示,
则D(0,0,0),E(0, ,1),A(1,0,0),C(0,1,0),
所以 =(0, ,1), =(-1,1,0),
则 ,
则异面直线DE与AC所成角的余弦值为 .
故答案为:B.
【分析】以D为原点建立空间直角坐标系如图所示,利用向量法求出异面直线DE与AC所成角的余弦值 。
3.(2021高二上·砀山月考)在空间直角坐标 中, 为坐标原点,若点 在平面 上的投影点为B,则线段OB的长度为( )
A. B. C. D.3
【答案】A
【考点】点、线、面间的距离计算
【解析】【解答】解:∵点B是点 在平面 上的投影点
∴点B为(1,0,2)
∴
故答案为:A
【分析】根据空间中两点距离公式求解即可.
4.(2021高二上·葫芦岛月考)若空间向量 , ,则 ( )
A. B.3 C. D.
【答案】D
【考点】空间向量的加减法;空间向量运算的坐标表示
【解析】【解答】解: ,
.
故答案为:D
【分析】利用已知条件结合向量加法坐标运算和向量模长的坐标表示,可以算出模长.
5.(2021高二上·浙江期中)如图,在直三棱柱 中, , 分别是棱 的中点,则异面直线 与 所成角的大小为( )
A.30° B.45° C.60° D.90°
【答案】B
【考点】用空间向量求直线间的夹角、距离
【解析】【解答】由题意以 为 轴建立空间直角坐标系,如图,
则 , . , , ,
, ,
,
所以 ,即异面直线 与 所成角是45 .
故答案为:B.
【分析】以 为 轴建立空间直角坐标系,用向量法求异面直线所成的角。
6.(2021高二上·沈阳期中)如图,在棱长为2的正方体ABCD A1B1C1D1中,E为BC的中点,点P在线段D1E上,点P到直线CC1的距离的最小值为( )
A. B. C. D.
【答案】A
【考点】点、线、面间的距离计算
【解析】【解答】以D为原点, 分别为x轴、y轴、z轴建立空间直角坐标系,
则E(1,2,0),D1(0,0,2), , ,
, , ,
设 (x,y,z), , ,
则 (x,y,z)·(0,0,2)=0,∴z=0,
=(x,y,z)·(-1,-2,2)= ,∴y=- x,
令x=1,则y=- ,∴u=(1,- ,0),
∴异面直线D1E与CC1的距离为d= ,
∵P在D1E上运动,∴P到直线CC1的距离的最小值为d= .
故答案为:A.
【分析】以D为原点, 分别为x轴、y轴、z轴建立空间直角坐标系,求出对应点的坐标,再利用平面向量数量积的运算可得y=- x,令x=1,则y=- ,利用向量表示出异面直线D1E与CC1的距离,可得答案。
7.(2021高二上·湖南月考)直三棱柱 中, 为等边三角形, ,则 与 所成角的余弦值为( )
A. B. C. D.
【答案】B
【考点】用空间向量求直线间的夹角、距离
【解析】【解答】取 的中点O,以 为x轴, 为y轴,
过O作与 平行的直线为z轴建立空间直角坐标系,
不妨设 ,则 ,
所以 ,
设 与 所成角的 ,
则 .
故答案为:B
【分析】以 为x轴, 为y轴,过O作与 平行的直线为z轴建立空间直角坐标系,利用向量法。求出异面直线 与 所成角的余弦值 。
8.(2021高二上·宾县月考)如图,在正方体 中,O是AC的中点,点P在线段 上,若直线OP与平面 所成的角为 ,则 的取值范围是( )
A. B. C. D.
【答案】B
【考点】用空间向量求直线与平面的夹角;同角三角函数间的基本关系
【解析】【解答】解:设正方体边长为2,建立如图所示空间直角坐标系,
则O(1,1,0),A1(2,0,2),B(2,2,0),C1(0,2,2),
设P(a,2-a,2)(0≤a≤2),则,
由于使,,
所以是平面A1BC1的法向量,
所以
∵0≤a≤2
∴,
∴,
∴,
∴,
∴,
又∵,
∴,
故答案为:B
【分析】先利用向量法求得直线OP与平面 所成的角的正弦值sinθ,再根据同角三角函数间的基本关系求解即可.
二、多选题
9.设 , 为空间中的任意两个非零向量,下列各式中正确的有( ).
A.
B.
C.
D.
【答案】A,D
【考点】空间向量的数量积运算
【解析】【解答】由数量积的性质和运算律可知AD是正确的;
而 运算后是实数, 没有这种运算,B不正确;
,C不正确.
故答案为:AD.
【分析】根据题意由数量积的运算性质以及向量的运算性质对选项逐一判断即可得出答案。
10.(2021高二上·大连期中)已知正方体的棱长为,点,分别是,的中点,在正方体内部且满足,则下列说法正确的是( )
A.直线平面
B.直线与平面所成的角为
C.直线与平面的距离为
D.点到直线的距离为
【答案】A,B,D
【考点】直线与平面平行的性质;直线与平面垂直的性质;空间向量的夹角与距离求解公式;用空间向量求直线与平面的夹角;用空间向量求平面间的夹角
【解析】【解答】平面,平面,,,,故平面,平面,故,同理可得,,故直线平面,A符合题意;
如图所示:连接 与 交于点 ,则 , , ,
故 平面 ,即 为直线 与平面 所成的角, ,B符合题意;
, 平面 ,故 平面 , 为 中点,连接 ,则 ,故 平面 , ,C不符合题意;
以 为 轴建立空间直角坐标系,
则 , ,
,点 到直线 的距离为 ,D符合题意.
故答案为:ABD.
【分析由线面垂直的性质定理和判定定理,结合正方体的几何性质即可判断出选项A正确;根据题意作出辅助线,由正方体的几何性质结合线面角的定义即可得出 为直线与平面所成的角,然后由三角形中的几何计算关系即可求出结果,由此判断出选项B正确;根据题意由线面平行的判定定理结合正方体的几何性质即可得出平面,然后由题意作出辅助线,结合中点的坐标以及点到直线的距离公式计算出结果,由此判断出选项C错误;根据题意建立空间直角坐标系求出各个点的坐标以及向量的坐标,再由空间向量的距离公式代入数值计算出结果,由此判断出选项D正确,从而得出答案。
11.(2022高三上·河北月考)如图,在正方体中,分别为的中点,则下列说法正确的是( )
A. B.平面
C.与所成的角的余弦值为 D.点到平面的距离为
【答案】A,D
【考点】异面直线及其所成的角;直线与平面平行的判定;直线与平面垂直的性质;点、线、面间的距离计算
【解析】【解答】A选项:取中点为,则易得:,故与,,可得平面,又平面,故,A符合题意;
B选项:若平面,则平面或在平面内,显然不成立,B不符合题意;
C选项:取中点为,则即为所求角,,故,D不符合题意;
D选项:三棱锥中,,
等边三角形的外接圆半径为,
所以到平面的距离为,D符合题意.
故答案为:AD
【分析】根据题意由正方体的几何性质以及线面垂直的性质定理即可得出线线垂直,由此判断出选项A正确;由线面平行的性质定理结合正方体的几何性质即可判断出选项B错误;由正方体的几何性质即可得出即为所求角,结合三角形中的几何计算关系计算出结果即可,由此判断出选项C错误;由三棱锥的几何性质即可求出边的大小,再由外接圆的几何性质计算出圆的半径,然后由点到平面的距离公式,代入数值计算出结果,由此即可判断出选项D正确,由此即可得出答案。
12.(2021·汕头模拟)正方体 ,的棱长为4,已知 平面α, ,则关于α β截此正方体所得截面的判断正确的是( )
A.α截得的截面形状可能为正三角形
B. 与截面α所成角的余弦值为
C.α截得的截面形状可能为正六边形
D.β截得的截面形状可能为正方形
【答案】A,B,C
【考点】用空间向量求直线与平面的夹角
【解析】【解答】解:A选项:为正三角形的情况为△B1CD1,故A正确;
B选项:不妨设截面a是△B1CD1,由于直线与平面所成角的余弦值等于直线与平面法向量所成角正弦值,且AC1为平面B1CD1的法向量,则∠A1AC1即为直线与法向量为夹角,
设夹角为θ,则其正弦值为,故B正确;
C选项:为正六边形的情况为A1D1,A1B1,B1B,BC,CD,D1D中点连线构成,故C正确;
D选项:由于直线AC1为体对角线,且,在正方体上任找一点(排除A1C1)与A1C1可构成平面β,但无法得到正方形截面,故D错误.
故答案为:ABC
【分析】根据正方体的几何特征,利用向量法求直线与平面所成的角,结合正三角形及正六边形的几何特征求解即可.
三、填空题
13.(2021高二上·玉溪月考) 是半径为2的球O表面上三个点, 的外接圆面积为 ,则球心O 到平面 的距离为
【答案】
【考点】点、线、面间的距离计算
【解析】【解答】解:由题意设球的半径为R, 的外接圆半径为r,
则由πr2=π,得r=1,
则球心O到平面 的距离为
故答案为:
【分析】根据圆的面积公式,结合点到平面的距离求解即可.
14.(2020高二上·蚌埠期末)正方体 中,点P是 的中点,则异面直线AP与 所成角的大小为 .
【答案】
【考点】异面直线及其所成的角;用空间向量求直线与平面的夹角
【解析】【解答】设正方体 的棱长为2,连接
在正方体 中,
所以 (或其补角)为异面直线AP与 所成角
所以
所以
故答案为:
【分析】首先根据题意由正方体的性质即可求出异面直线所成的角,再由夹角的数量积公式代入数值计算出夹角的余弦值,从而即可求出角的大小。
15.(2021高三上·南京月考)在三棱锥 中, 和 都是边长为 的正三角形, .若 为三棱锥 外接球上的动点,则点 到平面 距离的最大值为 .
【答案】
【考点】球的体积和表面积;球内接多面体;点、线、面间的距离计算
【解析】【解答】设 中点为 , 的外心为 , 的外心为 ,
过点 作面 的垂线,过点 作直线面 的垂线,
两条垂线的交点 即为三棱锥 外接球的球心,
因为 和 都是边长为 的正三角形,可得 ,
又 ,所以 ,所以 ,
又因为 , ,所以 面 ,
因为 平面 ,所以平面 平面 ,且 ,
所以四边形 是边长为1的正方形,所以外接球半径 ,
到平面 的距离 ,
故答案为: .
【分析】根据题意做出辅助线,由已知条件即可得出两条垂线的交点 即为三棱锥 外接球的球心,结合三棱锥的几何性质由勾股定理计算出线线垂直,然后由线面垂直的判定定理即可得证出 面 ,从而得到平面 平面 由此计算出外接球的半径值,从而得出答案。
16.(2021高二上·茂名期中)下列关于空间向量的命题中,
①若向量 , 与空间任意向量都不能构成基底,则 ;
②若非零向量 , , 满足 , ,则有 ;
③若 , , 是空间的一组基底,且 ,则 , , , 四点共面;
④若向量 , , ,是空间一组基底,则 , , 也是空间的一组基底.
上述命题中,正确的有 .
【答案】①③④
【考点】空间向量的基本定理及其意义
【解析】【解答】解:对于①, 若向量 , 与空间任意向量都不能构成基底,则向量 , 与空间任意向量都共面,则与必共线,即//,故①正确;
对于②, 若非零向量 , , 满足 , ,当非零向量 , , 不共面时, 与可以不平行,故②不正确;
对于③,因为 ,所以,
所以,所以共面,所以 , , , 四点共面,故③正确;
对于④,若向量 , ,是空间一组基底,则向量 , , 不共面,则对任意实数x,y都有,即,
所以 , , 不共面,所以 , , 也是空间的一组基底.故④正确.
故答案为:①③④
【分析】根据空间向量基本定理可知,能作为基底的向量一定是不共面的向量,由此对四个命题逐个分析可得答案.
四、解答题
17.(2021高二下·思明期中)如图,四边形 为正方形, 平面 ,点 分别为 的中点,且 , .
(1)证明: 平面 ;
(2)求二面角 的大小.
【答案】(1)解:证明:取 的中点为 ,连接
又 为 的中点,所以 ,且 ,
因为 ,且 ,
所以 ,且 ,
故四边形 为平行四边形,则
又 平面 , 平面 ,
所以 平面 ,
(2)因为 , , 平面 ,所以
而四边形 为正方形,所以可如图建立空间直角坐标系
, , ,
所以 , ,
设平面 的一个法向量为 ,则
∴ ,
同理可得平面 的一个法向量为
所以 ,
由图知二面角 为钝角,则大小为 .
【考点】直线与平面平行的判定;用空间向量求平面间的夹角
【解析】【分析】(1) 取 的中点为 ,连接 ,又因为 为 的中点,再利用中点作中位线的方法结合中位线的性质,所以 且 ,因为 且 ,
所以 且 ,故四边形 为平行四边形,则 ,再利用线线平行证出线面平行,从而证出直线 平面 。
(2) 因为 , , 平面 ,所以 ,而四边形 为正方形,所以可建立空间直角坐标系 ,从而求出点的坐标,再利用向量的坐标表示求出向量的坐标,再结合数量积求向量夹角公式,从而求出二面角 的大小。
18.(2021·绵阳模拟)如图,在四棱锥 中,四边形 为梯形, , , 平面 .
(1)求证:平面 平面 ;
(2)若 , ,求二面角 所成角的余弦值.
【答案】(1)证明:由 平面 ,且 平面 ,所以 .
又由 ,且 ,所以 平面 .
因为 平面 ,所以平面 平面 .
(2)解:建立如图所示空间直角坐标系 ,
因为 平面 , 平面 ,所以 .
由 , ,可得 , , ,
则 ,
设平面 的法向量为 ,
则 ,即得 ,取 ,得 , ,
所以平面 的一个法向量为 .
取平面 的一个法向量 ,
可得 .
因为二面角 所成角为锐角,所以二面角 的余弦值为 .
【考点】平面与平面垂直的判定;用空间向量求平面间的夹角
【解析】【分析】 (1)利用线面垂直的性质定理即可得出线线垂直,再结合线面垂直的判定定理即可得证出结论。
(2)建立合适的空间直角坐标系,求出所需点的坐标和向量的坐标,然后利用待定系数法求出平面的法向量,由向量的夹角公式求解即可.
19.(2022·邵阳模拟)如图,四棱锥A-BCDE的底面为等腰梯形,,且,,平面平面ACB.
(1)证明:.
(2)若,求二面角C-AD-E的大小.
【答案】(1)证明:因为平面平面ACB,且平面平面,
,平面ACB,所以平面ACD.
又因为平面ACD,所以.
(2)解:分别以 为轴,过点作平面的垂线为轴,如图,建立空间直角坐标系,连接BD.
由已知条件,易得,,.
在△BCD中,由余弦定理可得,所以.
在△ACD中,由余弦定理得,所以.
因为,所以,,
设为平面ADE的法向量,
由 ,得,取,则.
又平面ACD的一个法向量为.
所以.
又面角C-AD-E为钝角,所以二面角C-AD-E为.
【考点】数量积表示两个向量的夹角;直线与平面垂直的性质;平面与平面垂直的性质;用空间向量求平面间的夹角;余弦定理
【解析】【分析】(1)根据题意由面面垂直的性质定理即可得出线面垂直,再由线面垂直的性质定理即可得出线线垂直。
(2) 根据题意建立空间直角坐标系,由此求出点以及向量的坐标,然后由数量积的坐标公式计算出平面的法向量,再由向量夹角公式结合余弦定理代入数值计算出结果即可。
20.(2020高三上·泰安期末)如图,在四棱锥 中,底面 是菱形, , , 为 上一点,过 作与 平行的平面 ,分别交 , 于点 , .
(1)证明: 平面 ;
(2)若 为 的中点, ,直线 与平面 所成角为60°.求平面 与平面 所成锐二面角的余弦值.
【答案】(1)证明:连接 ,交 于点 ,连接 .
∵ 平面 ,平面 平面 , 平面 ,∴ .
∵底面 是菱形,∴ ,且 为 , 中点,
又 ,∴ ,又 , 平面 ,
∴ 平面 ,∴ 平面 .
(2)解:∵ ,∴ ,由(1)知 , , 平面 ,
∴ 平面 ,∴ .
∵ ,∴ , ,又 , ,∴ .
以 为原点, , , 所在直线分别为 轴, 轴, 轴,建立如图所示的空间直角坐标系,
则 , , , , ,
∴ , , , , ,
设平面 的一个法向量为 ,则 ,∴ .
令 ,解得 ,∴ .
设平面 的一个法向量为 ,则 ,
∴ .
令 ,解得 ,∴ ,
∴ , , .
∴ .
∴平面 与平面 所成锐二面角的余弦值为 .
【考点】直线与平面垂直的判定;直线与平面垂直的性质;空间向量的数量积运算;用空间向量求平面间的夹角
【解析】【分析】(1)根据题意作出辅助线再由线面平行的性质定理即可得出线线平行,结合菱形的性质以及中点的性质即可得出线线垂直,然后由线面垂直的判定定理即可得证出结论。
(2)由已知条件结合由(1)的结论即可得出线面垂直由此得出线线垂直,由此建立空间直角坐标系求出各个点的坐标以及向量的坐标,再由数量积的坐标公式即可求出平面的法向量的坐标,同理即可求出平面的法向量;结合空间数量积的运算公式代入数值即可求出夹角的余弦值,由此得到 平面 与平面 所成锐二面角的余弦值 。
21.(2021·商丘模拟)如图,在三棱锥 中,平面 平面 , , , , .
(1)证明: ;
(2)若 ,求二面角 的余弦值.
【答案】(1) , , ,
又平面 平面 , 平面 ,
.
, ,
又 , 平面 ,
又 平面 ,
.
(2)如图,分别以 , 所在直线为 轴, 轴,过 垂直于平面 的直线为 轴,建立空间直角坐标系.
则 , , , , .
, , ,
设 为平面 的法向量,
则 则可取 ,
设 为平面 的法向量,
则 则可取 ,
则 .
结合图形可知,二面角 的余弦值为 .
【考点】直线与平面垂直的判定;直线与平面垂直的性质;空间向量的数量积运算;用空间向量求平面间的夹角
【解析】【分析】(1)根据题意由等边三角形的几何关系即可得出线线垂直,再由线面垂直的判定定理和性质定理即可得出 平面 以及 ,结合勾股定理计算出垂直关系,再由线面垂直的判定定理即可得出 平面 ,由线面垂直的性质定理即可证出结论 。
(2)由(1)的结论即可得出线线垂直由此 分别以 , 所在直线为 轴, 轴,过 垂直于平面 的直线为 轴,建立空间直角坐标系,求出各个点的坐标以及向量和平面法向量的坐标,再由数量积的坐标公式即可求出平面的法向量的坐标,同理即可求出平面的法向量;结合空间数量积的运算公式代入数值即可求出夹角的余弦值,由此得到 二面角 的余弦值.
22.(2021高二上·六安开学考)如图所示,多面体ABCDEF中, 平面ABCD,四边形ABCD是菱形, , ,四边形BDEF是正方形.
(1)求证: 平面AED;
(2)求直线AF与平面ECF所成角的正弦值;
(3)在线段EC上是否存在点P,使得 平面CEF?若存在,求出 的值;若不存在,请说明理由.
【答案】(1)解:因为四边形ABCD是菱形,所以 .
又 平面ADE, 平面ADE,
所以 平面ADE,
又四边形BDEF是正方形,所以 .
因为 平面ADE, 平面ADE,
所以 平面ADE,
因为 平面BCF, 平面BCF, ,
所以平面 平面AED,
因为 平面BCF,所以 平面AED.
(2)因为四边形ABCD为菱形,且 ,
所以 为等边三角形,取BD的中点O,连接CO,所以 ,
取EF的中点G,连接OG,则 ,
因为 平面ABCD,所以 平面ABCD,
故可建立如图所示的空间直角坐标系 .
则 , , , , , ,
所以 , , .
设平面ECF的法向量为 ,
则有 ,得 ,
,令 ,则 .
设直线AF与平面ECF所成的角为 ,
则 ,
所以直线AF与平面ECF所成角的正弦值为 .
(3)不存在.理由如下:
由(2)得 , ,
设 , ,
由 ,
得 ,
由(2)得平面CEP的一个法向量为 .
若 平面CEF,则 ,令 ,
得 ,
方程组无解,不符合题意.
综上,线段EC上不存在点P,使得 平面CEF.
【考点】直线与平面平行的判定;平面与平面平行的判定;向量语言表述线面的垂直、平行关系;用空间向量求直线与平面的夹角
【解析】【分析】(1)根据直线与平面平行的判定定理,以及平面与平面平行的判定定理求证即可;
(2)建立恰当的空间直角坐标系,利用向量法直接求解即可;
(3)根据向量的坐标运算,结合向量法直接求解即可.
23
