精讲精练·专项突破 第一章《空间向量与几何》单元能力提升(含详细解析) (4)
文档属性
| 名称 | 精讲精练·专项突破 第一章《空间向量与几何》单元能力提升(含详细解析) (4) | 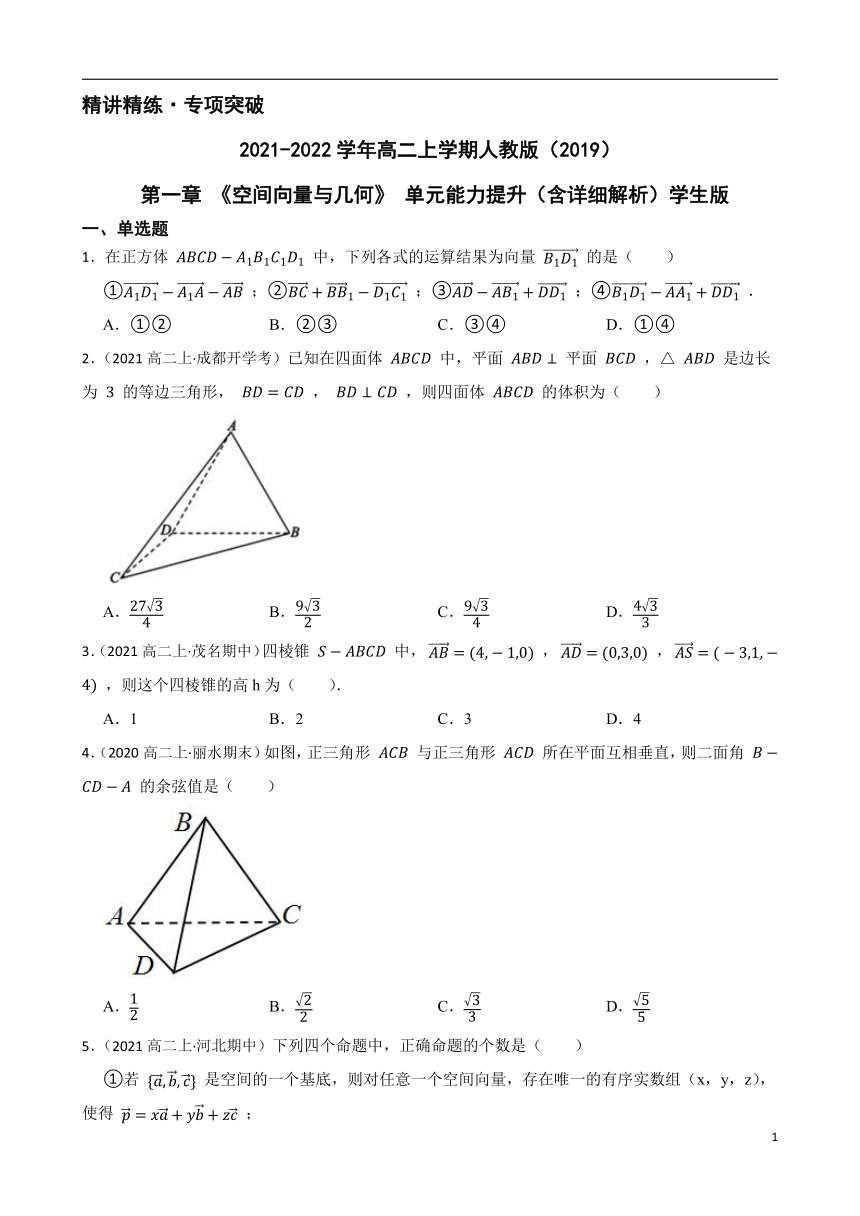 | |
| 格式 | docx | ||
| 文件大小 | 408.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-18 16:27:47 | ||
图片预览




文档简介
精讲精练·专项突破
2021-2022学年高二上学期人教版(2019)
第一章 《空间向量与几何》 单元能力提升(含详细解析)学生版
一、单选题
1.在正方体 中,下列各式的运算结果为向量 的是( )
① ;② ;③ ;④ .
A.①② B.②③ C.③④ D.①④
2.(2021高二上·成都开学考)已知在四面体 中,平面 平面 ,△ 是边长为 的等边三角形, , ,则四面体 的体积为( )
A. B. C. D.
3.(2021高二上·茂名期中)四棱锥 中, , , ,则这个四棱锥的高h为( ).
A.1 B.2 C.3 D.4
4.(2020高二上·丽水期末)如图,正三角形 与正三角形 所在平面互相垂直,则二面角 的余弦值是( )
A. B. C. D.
5.(2021高二上·河北期中)下列四个命题中,正确命题的个数是( )
①若 是空间的一个基底,则对任意一个空间向量,存在唯一的有序实数组(x,y,z),使得 ;
②若两条不同直线l,m的方向向量分别是 , ,则l∥m ;
③若 是空间的一个基底,且 ,则A,B,C,D四点共面;
④若两个不同平面α,β的法向量分别是 ,且 , ,则α∥β.
A.1 B.2 C.3 D.4
6.(2021高一下·抚州期末)已知正方体 的棱长为1,点 , 分别为线段 , 上的动点,点 在平面 内,则 的最小值是( )
A. B. C. D.
7.(2020高二上·金华期末)如图,在正方形中,点 分别是线段 上的动点,且 与 交于G, 在 与 之间滑动,但与 和 均不重合.在 任一确定位置,将四边形 沿直线 折起,使平面 平面 ,则下列选项中错误的是( )
A. 的角度不会发生变化
B. 与 所成的角先变小后变大
C. 与平面 所成的角变小
D.二面角 先变大后变小
8.(2021高二上·温州期末)四边形ABCD和ABEF都是正方形,且面面ABEF,M为线段AF上的点,当M从A向F运动时,点B到平面MEC的距离( )
A.越来越大 B.越来越小
C.先增大再减小 D.先减小再增大
二、多选题
9.(2021高二上·东莞月考)已知向量 ,则与 共线的向量 ( )
A. B.
C. D.
10.(2021高二上·广东期中)已知直线 的一个方向向量为 ,平面 的一个法向量为 ,则下列结论正确的有( )
A.若 ,则 B.若 ,则
C.若 ,则 D.若 ,则
11.(2021高一下·聊城期末)如图,平面 平面 直线 ,点 ,点 ,且 ,点 、 分别是线段 、 的中点.( )
A.当直线 与 相交时,交点一定在直线 上
B.当直线 与 异面时, 可能与 平行
C.当 、 、 、 四点共面且 时,
D.当 、 两点重合时,直线 与 不可能相交
12.(2021高二上·浙江开学考)正方体 的棱长为2, 、 、 分别是棱 、 、 的中点,下列结论正确的有( )
A. 面
B. 面
C.过 三点所得正方体的截面的面积为
D.面 与面 所成角的正切值为
三、填空题
13.(2021高二上·台州期末)在棱长为1的正方体中,点到平面的距离为 .
14.如图,在直三棱柱 中,若 ,则 .(用 表示)
15.已知空间的个基底 ,若 , 共线,则 , .
16.(2021高二下·安徽月考)如图,二面角 为 , , ,过 , 分别作 的垂线,垂足分别为 , ,若 , , ,则 的长度为 .
四、解答题
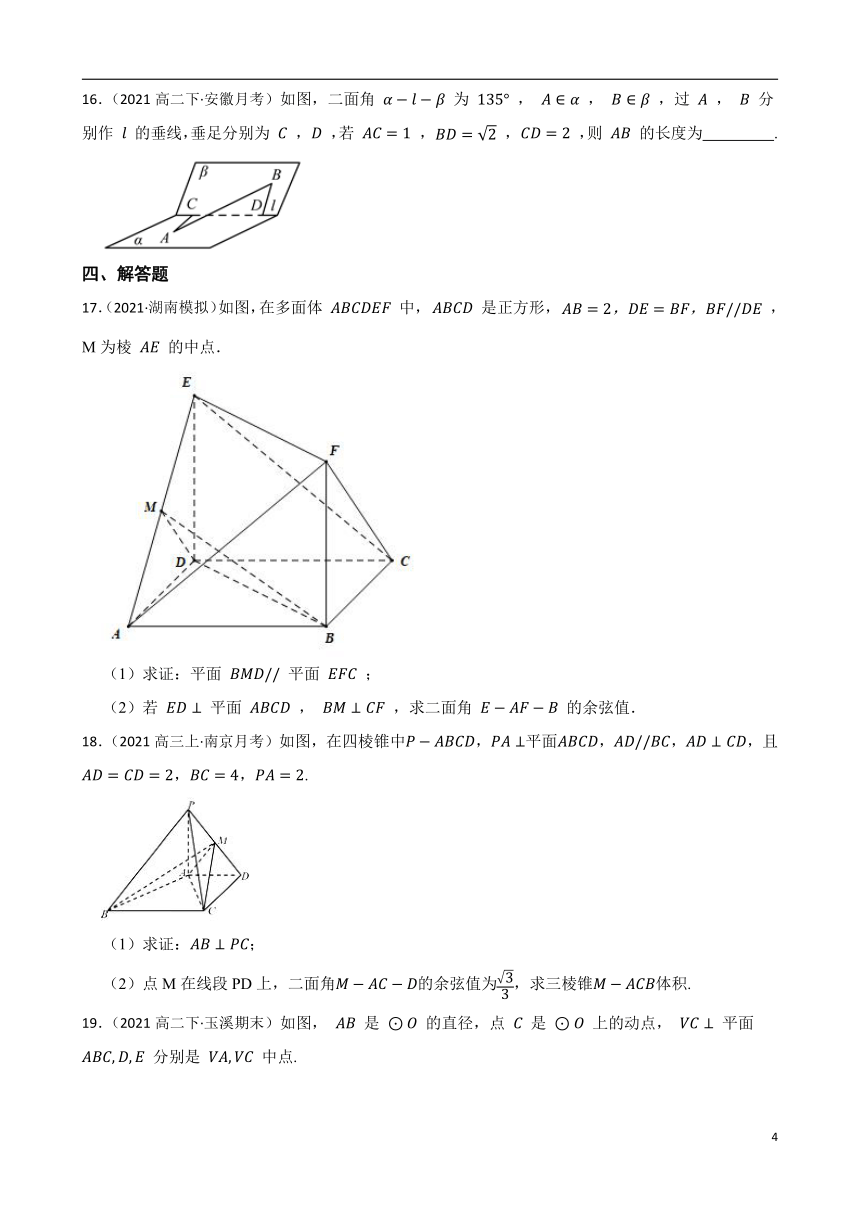
17.(2021·湖南模拟)如图,在多面体 中, 是正方形, ,M为棱 的中点.
(1)求证:平面 平面 ;
(2)若 平面 , ,求二面角 的余弦值.
18.(2021高三上·南京月考)如图,在四棱锥中,平面,,,且,,.
(1)求证:;
(2)点M在线段PD上,二面角的余弦值为,求三棱锥体积.
19.(2021高二下·玉溪期末)如图, 是 的直径,点 是 上的动点, 平面 分别是 中点.
(1)求证: ;
(2)当 时,求二面角 的正弦值.
20.(2022高三上·汕尾期末)如图,在五面体ABCDEF中,四边形ABCD为矩形,
(1)求证:平面ADE平面ABCD;
(2)若EF=ED=AD,CD=2EF=2,求平面ADE与平面BCF所成的锐二面角的大小.
21.(2021高二上·丰台期末)如图,在四棱锥中,底面是矩形,侧棱底面,点为棱的中点,,.
(1)求证:∥平面;
(2)求平面与平面夹角的余弦值;
(3)若为棱的中点,则棱上是否存在一点,使得平面. 若存在,求线段的长;若不存在,请说明理由.
22.(2021高二上·金华期末)在四棱锥 中,底面 是边长为2的菱形, 平面 , , 是 的中点.
(1)若 为线段 的中点,证明: 平面 ;
(2)线段 上是否存在点 ,使得直线 与平面 所成角的正弦值为 ,若存在,求 的长,若不存在,请说明理由.
答案解析部分
1.【答案】C
【考点】空间向量的加减法
【解析】【解答】 ,①错;
,②错;
,③对;
,④对.
故答案为:C.
【分析】结合正方体的几何性质以及向量的加减运算法则对选项逐一判断即可得出 ③④ 正确由此得出答案。
2.【答案】C
【考点】棱柱、棱锥、棱台的体积;平面与平面垂直的性质;点、线、面间的距离计算
【解析】【解答】由面 面 ,面 面 , , 面 ,
∴ 面 ,又等边△ 边长为 ,则 ,
由 ,故 .
故答案为:C
【分析】根据题意由面面垂直的性质定理即可得出线面垂直,由此得出点到平面的距离然后把数值代入到体积公式计算出结果即可。
3.【答案】D
【考点】点、线、面间的距离计算;向量的投影
【解析】【解答】解:设平面ABCD的法向量为,
则,即 ,∴ ,
取z=4,则 ,
∴这个四棱锥的高 ,
故选:D.
【分析】利用向量法直接求解即可.
4.【答案】D
【考点】空间向量的数量积运算;用空间向量求平面间的夹角
【解析】【解答】如图示,取AC中点E,连结BE、DE,在正三角形 与正三角形 中,
BE⊥AC,DE⊥AC,因为面 ⊥面 ,面 面 ,所以BE⊥面ADC,
以E为原点, 为x轴正方向, 为y轴正方向, 为z轴正方向,建立空间直角坐标系,设AC=2,则
,
平面ACD的一个法向量为
而 ,设 为面BCD的一个法向量,则:
即 ,不妨令x=1,则
设二面角 的平面角为θ,则θ为锐角,
所以 .
故答案为:D
【分析】首先由已知条件的面面垂直即可得出线面垂直,再由线面垂直的性质定理即可得出线线垂直由此建立空间直角坐标系求出各个点的坐标以及向量和平面ACD法向量的坐标,再由数量积的坐标公式即可求出平面BCD的法向量的坐标,结合空间数量积的运算公式代入数值即可求出夹角的余弦值,由此得到二面角的余弦值。
5.【答案】D
【考点】空间向量的基本定理及其意义;共线向量与共面向量;平面的法向量
【解析】【解答】①若 是空间的一个基底,则对任意一个空间向量,存在唯一的有序实数组(x,y,z),使得 ,由空间向量基本定理知,正确;
②若两条不同直线l,m的方向向量分别是 , ,则l∥m ,由方向向量的定义知,正确;
③若 是空间的一个基底,且 ,则A,B,C,D四点共面,由空间向量共面定理知,正确;
④若两个不同平面α,β的法向量分别是 ,且 , ,则α∥β.由法向量的定义知,正确.
故答案为:D
【分析】根据题意结合空间向量的基本定理,由此判断出 ① 正确;由直线的方向向量与向量共线的关系,由此判断出②正确;由空间向量共面定理即可判断出③正确;由平面的法向量的定义,结合平面平行的性质即可判断出④正确,从而即可得出答案。
6.【答案】B
【考点】点、线、面间的距离计算
【解析】【解答】解: 点关于 的对称点为 , 关于 的对称点为 ,
记 为直线 与 之间的距离,则 ,
由 , 为 到平面 的距离,
因为 ,
而 ,故 ,
故答案为:B.
【分析】 先根据对称性和三角不等式把问题转化为AB'与CE上两点连线长最小值问题,再利用异面直线距离求解.
7.【答案】D
【考点】数量积表示两个向量的夹角;用空间向量求直线与平面的夹角;用空间向量求平面间的夹角
【解析】【解答】以 为原点, , , 所在的直线为 轴,
建立空间直角坐标系,
设正方形的边长为 , ,
, , , , ,
对于A, , ,
,
故 的角度不会发生变化,所以A符合题意;
对于B,设 与 所成的角为 ,
, ,
,
对称轴为 ,且 ,所以 先减小后增加,
所以 先增加再减小,即 与 所成的角先变小后变大,B符合题意;
对于C,平面 的一个法向量为 ,
设 与平面 所成的角为 ,
,
,则 单调递减, 单调递减,
所以 与平面 所成的角变小,C符合题意;
对于D,设平面 的法向量为 ,
则 ,即 ,
令 , , ,
不妨设 ,
设平面 的一个法向量为 ,
则 , ,
令 , ,即 ,
,
对称轴为 ,在 先减小后增大,
所以 在 先减小后增大,
二面角 为钝角,
先增大后减小,
故二面角 先减小后增大,D不符合题意.
故答案为:D
【分析】以 为原点, , , 所在的直线为 轴,建立空间直角坐标系,进而求出点的坐标,再利用折叠的方法结合数量积求向量夹角公式和二次函数的图像的单调性,进而找出错误的选项。
8.【答案】A
【考点】点、线、面间的距离计算
【解析】【解答】设,,则,,,,,即,设点B到平面MEC的距离为,则,即,随着的增大,逐渐变小,则点B到平面MEC的距离越来越大。
故答案为:A
【分析】设,,再利用勾股定理得出,,,再结合余弦定理得出,再利用同角三角函数基本关系式,得出,再利用三角形的面积公式得出,设点B到平面MEC的距离为,再结合棱锥的体积公式和等体积法得出,随着的增大,逐渐变小,则点B到平面MEC的距离越来越大,从而选出正确的选项。
9.【答案】A,B,C
【考点】共线向量与共面向量
【解析】【解答】解:对于A,,则共线,故A正确;
对于B,,则共线,故B正确;
对于C,,则共线,故C正确;
对于D,不存在实数λ,使得,故D错误
【分析】根据共线向量的判定定理求解即可..
10.【答案】A,D
【考点】空间向量的数乘运算;空间向量运算的坐标表示
【解析】【解答】若 ,则 , ,即 ,A符合题意,C不符合题意;
若 ,得 , ,显然 , ,则 ,解得 ,B不符合题意,D符合题意.
故答案为:AD
【分析】若 ,则 ,再利用数量积为0两向量垂直的等价关系,再结合数量积的坐标表示,进而得出;若 ,得 , 再结合向量共线的坐标表示,进而得出,从而选出正确的结论。
11.【答案】A,C,D
【考点】空间点、线、面的位置
【解析】【解答】对于A,设 ,因为 , ,所以 ,A项正确;
对于B,当 、 是异面直线时,假设 ,则 平面 ,连接 ,取 的中点 ,连接 、 ,因为 、 分别为 、 的中点,所以 ,所以平面 平面 ,同理可得平面 平面 ,所以平面 平面 ,与已知矛盾,故假设不成立,所以 不可能与 平行,B项错误;
对于C,若 、 、 、 四点共面且 时,可得 平面 ,过 的平面 与平面 相交于 ,所以 ,C项正确;
对于D,若 、 两点重合,则 ,故 ,此时直线 与直线 不可能相交,D项正确.
故答案为:ACD
【分析】利用已知条件结合中点的性质,再利用直线与直线的位置关系结合四点共面的判断方法,从而推出线线的位置关系以及点与直线的位置关系,从而找出正确的选项。
12.【答案】A,B,C
【考点】向量语言表述线面的垂直、平行关系;用空间向量求平面间的夹角;三角形中的几何计算
【解析】【解答】解:
建立如图的空间直角坐标系,则D(0,0,0),A1(2,0,2),C1(0,2,2),E(2,0,1),F(0,1,2),
G(1,2,0),B1(2,2,2)
,
设平面EFG的法向量为,
则由,则令y=1,得x=1,z=1,则
对于A,∵
∴
则A1C1//面EFG,故A正确;
对于B,∵
∴与共线
∴B1D⊥面EFG
故B正确;
对于C,
分别取AB,CC1,A1D1的中点J,I,H,连接EJ,JG,GI,IF,FH,HE,易知过EFG三点所得正方体的截面是正六边形EJGIFH,且正六边形的边长为,则其面积为,故C正确;
对于D,易知平面ABCD的为,设面 与面 所成角为θ,显然θ为锐角,
则,则
∴
故D错误
故答案为:ABC
【分析】根据直线与平面平行的判定定理,结合向量法可判断A,根据直线与平面垂直的判定定理,结合向量法可判断B,根据三角形面积公式可判断C,根据平面与平面所成角的定义,结合向量法可判断D
13.【答案】
【考点】点、线、面间的距离计算
【解析】【解答】由题设可得示意图如下,根据正方体的性质知:面面,又△为等腰直角三角形,
∴△斜边上的高,即为到平面的距离,又因为正方体棱长为1,
∴到平面的距离为。
故答案为:。
【分析】由题设结合正方体的性质知:面面,再利用三角形△为等腰直角三角形,得出三角形△斜边上的高,即为到平面的距离,再利用正方体棱长为1,从而得出点到平面的距离。
14.【答案】
【考点】空间向量的加减法
【解析】【解答】在直三棱柱 中,若 ,
则
故答案为:
【分析】由向量的加、减法运算法则计算出结果即可。
15.【答案】1;-1
【考点】共线向量与共面向量
【解析】【解答】∵ , 共线,∴ ,使 ,
∴ ,得
解得
故答案为:1,-1
【分析】由空间向量共面的性质定理得到关于x、y、的方程组求解出结果即可。
16.【答案】3
【考点】点、线、面间的距离计算
【解析】【解答】因为 , , ,所以
,又因为二面角 为 ,所以 ,所以 .
故答案为:3.
【分析】 , , ,结合空间向量距离公式,转化求解即可.
17.【答案】(1)证明:如图,连接 ,交 于点N,
∴N为 的中点,
连接 ,由M为棱 的中点,则 .
∵ 面 , 面 ,∴ 平面 .
∵ ,∴四边形 为平行四边形,
∴ .又 平面 , 平面 ,
∴ 平面 ,又 ,
∴平面 平面 .
(2)解:∵ 平面 是正方形
∴分别以 为x轴、y轴、z轴,建立空间直角坐标系,
设 ,
则
设平面 的法向量为 ,则
∵ 平面 平面 ,又
∴ 平面 ,∴平面 的法向量为 .
,
由图可知二面角 为钝角,
∴二面角的 余弦值为 .
【考点】平面与平面平行的判定;用空间向量求平面间的夹角
【解析】【分析】(1)首先由已知条件作出辅助线,再由中点的性质得到线线平行,由线线平行得出四边形 为平行四边形,再由线面平行以及面面平行的判定定理即可得证出结论。
(2)根据题意由线面垂直的性质定理得出线线垂直,由此建立空间直角坐标系求出各个点的坐标以及向量和平面法向量的坐标,再由数量积的坐标公式即可求出平面的法向量的坐标,同理即可求出平面的法向量;结合空间数量积的运算公式代入数值即可求出夹角的余弦值,由此得到 二面角的 余弦值。
18.【答案】(1)∵四边形是直角梯形,,,
∴,,
∴是等腰直角三角形,即,
∵平面,平面,
∴,
又,
∴平面,
又面,
∴.
(2)过点作于E,以点为原点,AE,AD,AP所在直线分别为x轴,y轴,z轴建立平面直角坐标系,
取平面DAC的法向量.
设,,,
设平面的法向量为,
由,,得,可取,
所以,得.
故.
【考点】棱柱、棱锥、棱台的体积;直线与平面垂直的判定;直线与平面垂直的性质;与二面角有关的立体几何综合题;用空间向量求平面间的夹角
【解析】【分析】(1)由已知条件结合梯形的几何性质即可得出边的大小,然后由勾股定理计算出边的大小,结合三角形中的几何计算关系即可得出线线垂直,再由线面垂直的判定定理和性质定理即可得出线线垂直,由此即可得证出结论。
(2)根据题意建立空间直角坐标系求出各个点的坐标以及向量和平面DAC法向量的坐标,再由数量积的坐标公式即可求出平面DAC的法向量的坐标,同理即可求出平面的法向量;结合空间数量积的运算公式代入数值即可求出夹角的余弦值从而计算出a的取值,再由等体积法代入数值计算出结果即可。
19.【答案】(1)因为 是 的直径,点 是 上的动点,所以 , 平面 , 面 ,所以 , , 面 ,所以 面 ,因为 分别是 中点,所以 ,所以 面 ,因为 面 ,所以
(2)如图建立空间直角坐标系,则 , , , ,
所以 , ,
显然面 的法向量可以为 ,设面 的法向量为 ,则 ,令 ,则 , ,所以 ,设二面角 为 ,则
所以 ,所以二面角 的正弦值为
【考点】空间中直线与直线之间的位置关系;用空间向量求平面间的夹角;同角三角函数间的基本关系
【解析】【分析】(1) 利用 是 的直径,点 是 上的动点,所以 , 再利用 平面 ,从而利用线面垂直的定义证出线线垂直,所以 ,再利用线线垂直证出线面垂直,所以 面 ,再利用 分别是 中点结合中点作中位线的方法结合中位线的性质,所以 ,所以 面 ,再利用线面垂直的定义证出线线垂直,从而证出 。
(2)利用已知条件建立空间直角坐标系, 从而求出点的坐标,再利用向量的坐标表示求出向量的坐标,再利用数量积求向量夹角的公式,从而结合同角三角函数基本关系式求出二面角 的正弦值。
20.【答案】(1)证明:∵四边形为矩形,
∴,
又∵,,平面,平面,
∴平面,
∵平面,
∴平面平面
(2)解:∵平面,平面,
∴
∵,平面,平面,,
∴平面,
∴以点D为原点,以DA方向为x轴正方向,以DC方向为y轴正方向,以DE方向为z轴正方向,建立空间直角坐标系,如图,
则,
∴,
∵平面,
∴平面的一个法向量是,
设平面的法向量是,
则,即,令,则,
∴一个法向量,
∴
∴平面与平面所成的锐二面角的大小为
【考点】平面与平面垂直的判定;用空间向量求平面间的夹角
【解析】【分析】(1) 利用四边形为矩形,所以,再利用结合线线垂直证出线面垂直,所以平面,再利用线面垂直证出面面垂直,从而证出平面ADE平面ABCD。
(2)利用直线 平面结合线面垂直的定义证出线线垂直,所以,再利用结合线线垂直证出线面垂直,所以平面,所以以点D为原点,以DA方向为x轴正方向,以DC方向为y轴正方向,以DE方向为z轴正方向,建立空间直角坐标系,从而求出点的坐标,再结合向量的坐标表示求出向量的坐标,再结合数量积求向量夹角公式,进而求出平面ADE与平面BCF所成的锐二面角的大小。
21.【答案】(1)证明:因为底面是矩形,所以.
因为平面,所以,
.以为原点,,,
所在直线分别为轴、轴,轴,建立
如图所示的空间直角坐标系,
则(0,0,0),(1,0,0),(1,2,0),(0,2,0),(0,0,2),(0,1,1),
所以(1,2,0),(0,1,1),(1,0,2).
设平面的一个法向量为,
则,即
取,则,.
所以是平面的一个法向量.
因为,且平面,
所以//平面
(2)解:由(1)可知,,
又因为,所以平面.
所以(0,2,0)是平面的一个法向量.
设平面与平面的夹角为,
则
所以平面与平面夹角的余弦值为.
(3)解:因为为的中点,所以(,1,1),所以(,0,0).
又因为(1,2,2),所以,
所以与不垂直.
而平面,
所以棱上不存在点,使得平面.
【考点】向量语言表述线面的垂直、平行关系;用空间向量求平面间的夹角
【解析】【分析】(1)以为原点,,,所在直线分别为轴、轴,轴,建立空间直角坐标系, 求得平面ACE的一个法向量,由 证明出 //平面 ;
(2)易知 (0,2,0)是平面的一个法向量,设平面与平面的夹角为, 利用向量法即可求出平面与平面夹角的余弦值;
(3)求出的坐标,根据 ,判断出与不垂直,可得棱上不存在点,使得平面.
22.【答案】(1)证明:取 的中点为 ,连接 ,
因为 分别为 的中点,所以 ,
又因为 平面 ,且 ,
所以平面 平面 ,
又由 平面 ,所以 平面 .
(2)解:以 为原点, 所在的直线分别为 轴、 轴,以垂直平面 的直线为 轴,建立空间直角坐标系,如图所示,
因为底面 是边长为2的菱形,设 ,
在直角 中,可得 ,
在直角 中,可得 ,
在 中,因为 ,所以 ,
即 ,解得 ,
设 ,可得 ,
则 ,
设平面 的法向量为 ,则 ,
令 ,可得 ,
设直线 与平面 所成角为 ,
所以 ,解得 ,即 ,
所以存在点 ,且 的长为 .
【考点】直线与平面平行的判定;用空间向量求直线与平面的夹角
【解析】【分析】 (1)取 的中点为 ,连接 ,利用 分别为 的中点,再结合中点作中位线的方法和中位线的性质,所以 ,再利用线线平行证出线面平行,再结合线面平行证出面面平行,所以平面 平面 ,再结合面面平行的性质定理证出线面平行,从而证出直线 平面 。
(2) 以 为原点, 所在的直线分别为 轴、z轴,以垂直平面 的直线为 轴,建立空间直角坐标系, 从而求出点的坐标,再结合向量的坐标表示求出向量的坐标,再利用数量积求向量夹角公式得出直线 与平面 所成角的正弦值,再结合直线 与平面 所成角的正弦值为 ,从而得出点M的坐标,进而得出存在点 ,并求出此时对应的 的长。
25
2021-2022学年高二上学期人教版(2019)
第一章 《空间向量与几何》 单元能力提升(含详细解析)学生版
一、单选题
1.在正方体 中,下列各式的运算结果为向量 的是( )
① ;② ;③ ;④ .
A.①② B.②③ C.③④ D.①④
2.(2021高二上·成都开学考)已知在四面体 中,平面 平面 ,△ 是边长为 的等边三角形, , ,则四面体 的体积为( )
A. B. C. D.
3.(2021高二上·茂名期中)四棱锥 中, , , ,则这个四棱锥的高h为( ).
A.1 B.2 C.3 D.4
4.(2020高二上·丽水期末)如图,正三角形 与正三角形 所在平面互相垂直,则二面角 的余弦值是( )
A. B. C. D.
5.(2021高二上·河北期中)下列四个命题中,正确命题的个数是( )
①若 是空间的一个基底,则对任意一个空间向量,存在唯一的有序实数组(x,y,z),使得 ;
②若两条不同直线l,m的方向向量分别是 , ,则l∥m ;
③若 是空间的一个基底,且 ,则A,B,C,D四点共面;
④若两个不同平面α,β的法向量分别是 ,且 , ,则α∥β.
A.1 B.2 C.3 D.4
6.(2021高一下·抚州期末)已知正方体 的棱长为1,点 , 分别为线段 , 上的动点,点 在平面 内,则 的最小值是( )
A. B. C. D.
7.(2020高二上·金华期末)如图,在正方形中,点 分别是线段 上的动点,且 与 交于G, 在 与 之间滑动,但与 和 均不重合.在 任一确定位置,将四边形 沿直线 折起,使平面 平面 ,则下列选项中错误的是( )
A. 的角度不会发生变化
B. 与 所成的角先变小后变大
C. 与平面 所成的角变小
D.二面角 先变大后变小
8.(2021高二上·温州期末)四边形ABCD和ABEF都是正方形,且面面ABEF,M为线段AF上的点,当M从A向F运动时,点B到平面MEC的距离( )
A.越来越大 B.越来越小
C.先增大再减小 D.先减小再增大
二、多选题
9.(2021高二上·东莞月考)已知向量 ,则与 共线的向量 ( )
A. B.
C. D.
10.(2021高二上·广东期中)已知直线 的一个方向向量为 ,平面 的一个法向量为 ,则下列结论正确的有( )
A.若 ,则 B.若 ,则
C.若 ,则 D.若 ,则
11.(2021高一下·聊城期末)如图,平面 平面 直线 ,点 ,点 ,且 ,点 、 分别是线段 、 的中点.( )
A.当直线 与 相交时,交点一定在直线 上
B.当直线 与 异面时, 可能与 平行
C.当 、 、 、 四点共面且 时,
D.当 、 两点重合时,直线 与 不可能相交
12.(2021高二上·浙江开学考)正方体 的棱长为2, 、 、 分别是棱 、 、 的中点,下列结论正确的有( )
A. 面
B. 面
C.过 三点所得正方体的截面的面积为
D.面 与面 所成角的正切值为
三、填空题
13.(2021高二上·台州期末)在棱长为1的正方体中,点到平面的距离为 .
14.如图,在直三棱柱 中,若 ,则 .(用 表示)
15.已知空间的个基底 ,若 , 共线,则 , .
16.(2021高二下·安徽月考)如图,二面角 为 , , ,过 , 分别作 的垂线,垂足分别为 , ,若 , , ,则 的长度为 .
四、解答题
17.(2021·湖南模拟)如图,在多面体 中, 是正方形, ,M为棱 的中点.
(1)求证:平面 平面 ;
(2)若 平面 , ,求二面角 的余弦值.
18.(2021高三上·南京月考)如图,在四棱锥中,平面,,,且,,.
(1)求证:;
(2)点M在线段PD上,二面角的余弦值为,求三棱锥体积.
19.(2021高二下·玉溪期末)如图, 是 的直径,点 是 上的动点, 平面 分别是 中点.
(1)求证: ;
(2)当 时,求二面角 的正弦值.
20.(2022高三上·汕尾期末)如图,在五面体ABCDEF中,四边形ABCD为矩形,
(1)求证:平面ADE平面ABCD;
(2)若EF=ED=AD,CD=2EF=2,求平面ADE与平面BCF所成的锐二面角的大小.
21.(2021高二上·丰台期末)如图,在四棱锥中,底面是矩形,侧棱底面,点为棱的中点,,.
(1)求证:∥平面;
(2)求平面与平面夹角的余弦值;
(3)若为棱的中点,则棱上是否存在一点,使得平面. 若存在,求线段的长;若不存在,请说明理由.
22.(2021高二上·金华期末)在四棱锥 中,底面 是边长为2的菱形, 平面 , , 是 的中点.
(1)若 为线段 的中点,证明: 平面 ;
(2)线段 上是否存在点 ,使得直线 与平面 所成角的正弦值为 ,若存在,求 的长,若不存在,请说明理由.
答案解析部分
1.【答案】C
【考点】空间向量的加减法
【解析】【解答】 ,①错;
,②错;
,③对;
,④对.
故答案为:C.
【分析】结合正方体的几何性质以及向量的加减运算法则对选项逐一判断即可得出 ③④ 正确由此得出答案。
2.【答案】C
【考点】棱柱、棱锥、棱台的体积;平面与平面垂直的性质;点、线、面间的距离计算
【解析】【解答】由面 面 ,面 面 , , 面 ,
∴ 面 ,又等边△ 边长为 ,则 ,
由 ,故 .
故答案为:C
【分析】根据题意由面面垂直的性质定理即可得出线面垂直,由此得出点到平面的距离然后把数值代入到体积公式计算出结果即可。
3.【答案】D
【考点】点、线、面间的距离计算;向量的投影
【解析】【解答】解:设平面ABCD的法向量为,
则,即 ,∴ ,
取z=4,则 ,
∴这个四棱锥的高 ,
故选:D.
【分析】利用向量法直接求解即可.
4.【答案】D
【考点】空间向量的数量积运算;用空间向量求平面间的夹角
【解析】【解答】如图示,取AC中点E,连结BE、DE,在正三角形 与正三角形 中,
BE⊥AC,DE⊥AC,因为面 ⊥面 ,面 面 ,所以BE⊥面ADC,
以E为原点, 为x轴正方向, 为y轴正方向, 为z轴正方向,建立空间直角坐标系,设AC=2,则
,
平面ACD的一个法向量为
而 ,设 为面BCD的一个法向量,则:
即 ,不妨令x=1,则
设二面角 的平面角为θ,则θ为锐角,
所以 .
故答案为:D
【分析】首先由已知条件的面面垂直即可得出线面垂直,再由线面垂直的性质定理即可得出线线垂直由此建立空间直角坐标系求出各个点的坐标以及向量和平面ACD法向量的坐标,再由数量积的坐标公式即可求出平面BCD的法向量的坐标,结合空间数量积的运算公式代入数值即可求出夹角的余弦值,由此得到二面角的余弦值。
5.【答案】D
【考点】空间向量的基本定理及其意义;共线向量与共面向量;平面的法向量
【解析】【解答】①若 是空间的一个基底,则对任意一个空间向量,存在唯一的有序实数组(x,y,z),使得 ,由空间向量基本定理知,正确;
②若两条不同直线l,m的方向向量分别是 , ,则l∥m ,由方向向量的定义知,正确;
③若 是空间的一个基底,且 ,则A,B,C,D四点共面,由空间向量共面定理知,正确;
④若两个不同平面α,β的法向量分别是 ,且 , ,则α∥β.由法向量的定义知,正确.
故答案为:D
【分析】根据题意结合空间向量的基本定理,由此判断出 ① 正确;由直线的方向向量与向量共线的关系,由此判断出②正确;由空间向量共面定理即可判断出③正确;由平面的法向量的定义,结合平面平行的性质即可判断出④正确,从而即可得出答案。
6.【答案】B
【考点】点、线、面间的距离计算
【解析】【解答】解: 点关于 的对称点为 , 关于 的对称点为 ,
记 为直线 与 之间的距离,则 ,
由 , 为 到平面 的距离,
因为 ,
而 ,故 ,
故答案为:B.
【分析】 先根据对称性和三角不等式把问题转化为AB'与CE上两点连线长最小值问题,再利用异面直线距离求解.
7.【答案】D
【考点】数量积表示两个向量的夹角;用空间向量求直线与平面的夹角;用空间向量求平面间的夹角
【解析】【解答】以 为原点, , , 所在的直线为 轴,
建立空间直角坐标系,
设正方形的边长为 , ,
, , , , ,
对于A, , ,
,
故 的角度不会发生变化,所以A符合题意;
对于B,设 与 所成的角为 ,
, ,
,
对称轴为 ,且 ,所以 先减小后增加,
所以 先增加再减小,即 与 所成的角先变小后变大,B符合题意;
对于C,平面 的一个法向量为 ,
设 与平面 所成的角为 ,
,
,则 单调递减, 单调递减,
所以 与平面 所成的角变小,C符合题意;
对于D,设平面 的法向量为 ,
则 ,即 ,
令 , , ,
不妨设 ,
设平面 的一个法向量为 ,
则 , ,
令 , ,即 ,
,
对称轴为 ,在 先减小后增大,
所以 在 先减小后增大,
二面角 为钝角,
先增大后减小,
故二面角 先减小后增大,D不符合题意.
故答案为:D
【分析】以 为原点, , , 所在的直线为 轴,建立空间直角坐标系,进而求出点的坐标,再利用折叠的方法结合数量积求向量夹角公式和二次函数的图像的单调性,进而找出错误的选项。
8.【答案】A
【考点】点、线、面间的距离计算
【解析】【解答】设,,则,,,,,即,设点B到平面MEC的距离为,则,即,随着的增大,逐渐变小,则点B到平面MEC的距离越来越大。
故答案为:A
【分析】设,,再利用勾股定理得出,,,再结合余弦定理得出,再利用同角三角函数基本关系式,得出,再利用三角形的面积公式得出,设点B到平面MEC的距离为,再结合棱锥的体积公式和等体积法得出,随着的增大,逐渐变小,则点B到平面MEC的距离越来越大,从而选出正确的选项。
9.【答案】A,B,C
【考点】共线向量与共面向量
【解析】【解答】解:对于A,,则共线,故A正确;
对于B,,则共线,故B正确;
对于C,,则共线,故C正确;
对于D,不存在实数λ,使得,故D错误
【分析】根据共线向量的判定定理求解即可..
10.【答案】A,D
【考点】空间向量的数乘运算;空间向量运算的坐标表示
【解析】【解答】若 ,则 , ,即 ,A符合题意,C不符合题意;
若 ,得 , ,显然 , ,则 ,解得 ,B不符合题意,D符合题意.
故答案为:AD
【分析】若 ,则 ,再利用数量积为0两向量垂直的等价关系,再结合数量积的坐标表示,进而得出;若 ,得 , 再结合向量共线的坐标表示,进而得出,从而选出正确的结论。
11.【答案】A,C,D
【考点】空间点、线、面的位置
【解析】【解答】对于A,设 ,因为 , ,所以 ,A项正确;
对于B,当 、 是异面直线时,假设 ,则 平面 ,连接 ,取 的中点 ,连接 、 ,因为 、 分别为 、 的中点,所以 ,所以平面 平面 ,同理可得平面 平面 ,所以平面 平面 ,与已知矛盾,故假设不成立,所以 不可能与 平行,B项错误;
对于C,若 、 、 、 四点共面且 时,可得 平面 ,过 的平面 与平面 相交于 ,所以 ,C项正确;
对于D,若 、 两点重合,则 ,故 ,此时直线 与直线 不可能相交,D项正确.
故答案为:ACD
【分析】利用已知条件结合中点的性质,再利用直线与直线的位置关系结合四点共面的判断方法,从而推出线线的位置关系以及点与直线的位置关系,从而找出正确的选项。
12.【答案】A,B,C
【考点】向量语言表述线面的垂直、平行关系;用空间向量求平面间的夹角;三角形中的几何计算
【解析】【解答】解:
建立如图的空间直角坐标系,则D(0,0,0),A1(2,0,2),C1(0,2,2),E(2,0,1),F(0,1,2),
G(1,2,0),B1(2,2,2)
,
设平面EFG的法向量为,
则由,则令y=1,得x=1,z=1,则
对于A,∵
∴
则A1C1//面EFG,故A正确;
对于B,∵
∴与共线
∴B1D⊥面EFG
故B正确;
对于C,
分别取AB,CC1,A1D1的中点J,I,H,连接EJ,JG,GI,IF,FH,HE,易知过EFG三点所得正方体的截面是正六边形EJGIFH,且正六边形的边长为,则其面积为,故C正确;
对于D,易知平面ABCD的为,设面 与面 所成角为θ,显然θ为锐角,
则,则
∴
故D错误
故答案为:ABC
【分析】根据直线与平面平行的判定定理,结合向量法可判断A,根据直线与平面垂直的判定定理,结合向量法可判断B,根据三角形面积公式可判断C,根据平面与平面所成角的定义,结合向量法可判断D
13.【答案】
【考点】点、线、面间的距离计算
【解析】【解答】由题设可得示意图如下,根据正方体的性质知:面面,又△为等腰直角三角形,
∴△斜边上的高,即为到平面的距离,又因为正方体棱长为1,
∴到平面的距离为。
故答案为:。
【分析】由题设结合正方体的性质知:面面,再利用三角形△为等腰直角三角形,得出三角形△斜边上的高,即为到平面的距离,再利用正方体棱长为1,从而得出点到平面的距离。
14.【答案】
【考点】空间向量的加减法
【解析】【解答】在直三棱柱 中,若 ,
则
故答案为:
【分析】由向量的加、减法运算法则计算出结果即可。
15.【答案】1;-1
【考点】共线向量与共面向量
【解析】【解答】∵ , 共线,∴ ,使 ,
∴ ,得
解得
故答案为:1,-1
【分析】由空间向量共面的性质定理得到关于x、y、的方程组求解出结果即可。
16.【答案】3
【考点】点、线、面间的距离计算
【解析】【解答】因为 , , ,所以
,又因为二面角 为 ,所以 ,所以 .
故答案为:3.
【分析】 , , ,结合空间向量距离公式,转化求解即可.
17.【答案】(1)证明:如图,连接 ,交 于点N,
∴N为 的中点,
连接 ,由M为棱 的中点,则 .
∵ 面 , 面 ,∴ 平面 .
∵ ,∴四边形 为平行四边形,
∴ .又 平面 , 平面 ,
∴ 平面 ,又 ,
∴平面 平面 .
(2)解:∵ 平面 是正方形
∴分别以 为x轴、y轴、z轴,建立空间直角坐标系,
设 ,
则
设平面 的法向量为 ,则
∵ 平面 平面 ,又
∴ 平面 ,∴平面 的法向量为 .
,
由图可知二面角 为钝角,
∴二面角的 余弦值为 .
【考点】平面与平面平行的判定;用空间向量求平面间的夹角
【解析】【分析】(1)首先由已知条件作出辅助线,再由中点的性质得到线线平行,由线线平行得出四边形 为平行四边形,再由线面平行以及面面平行的判定定理即可得证出结论。
(2)根据题意由线面垂直的性质定理得出线线垂直,由此建立空间直角坐标系求出各个点的坐标以及向量和平面法向量的坐标,再由数量积的坐标公式即可求出平面的法向量的坐标,同理即可求出平面的法向量;结合空间数量积的运算公式代入数值即可求出夹角的余弦值,由此得到 二面角的 余弦值。
18.【答案】(1)∵四边形是直角梯形,,,
∴,,
∴是等腰直角三角形,即,
∵平面,平面,
∴,
又,
∴平面,
又面,
∴.
(2)过点作于E,以点为原点,AE,AD,AP所在直线分别为x轴,y轴,z轴建立平面直角坐标系,
取平面DAC的法向量.
设,,,
设平面的法向量为,
由,,得,可取,
所以,得.
故.
【考点】棱柱、棱锥、棱台的体积;直线与平面垂直的判定;直线与平面垂直的性质;与二面角有关的立体几何综合题;用空间向量求平面间的夹角
【解析】【分析】(1)由已知条件结合梯形的几何性质即可得出边的大小,然后由勾股定理计算出边的大小,结合三角形中的几何计算关系即可得出线线垂直,再由线面垂直的判定定理和性质定理即可得出线线垂直,由此即可得证出结论。
(2)根据题意建立空间直角坐标系求出各个点的坐标以及向量和平面DAC法向量的坐标,再由数量积的坐标公式即可求出平面DAC的法向量的坐标,同理即可求出平面的法向量;结合空间数量积的运算公式代入数值即可求出夹角的余弦值从而计算出a的取值,再由等体积法代入数值计算出结果即可。
19.【答案】(1)因为 是 的直径,点 是 上的动点,所以 , 平面 , 面 ,所以 , , 面 ,所以 面 ,因为 分别是 中点,所以 ,所以 面 ,因为 面 ,所以
(2)如图建立空间直角坐标系,则 , , , ,
所以 , ,
显然面 的法向量可以为 ,设面 的法向量为 ,则 ,令 ,则 , ,所以 ,设二面角 为 ,则
所以 ,所以二面角 的正弦值为
【考点】空间中直线与直线之间的位置关系;用空间向量求平面间的夹角;同角三角函数间的基本关系
【解析】【分析】(1) 利用 是 的直径,点 是 上的动点,所以 , 再利用 平面 ,从而利用线面垂直的定义证出线线垂直,所以 ,再利用线线垂直证出线面垂直,所以 面 ,再利用 分别是 中点结合中点作中位线的方法结合中位线的性质,所以 ,所以 面 ,再利用线面垂直的定义证出线线垂直,从而证出 。
(2)利用已知条件建立空间直角坐标系, 从而求出点的坐标,再利用向量的坐标表示求出向量的坐标,再利用数量积求向量夹角的公式,从而结合同角三角函数基本关系式求出二面角 的正弦值。
20.【答案】(1)证明:∵四边形为矩形,
∴,
又∵,,平面,平面,
∴平面,
∵平面,
∴平面平面
(2)解:∵平面,平面,
∴
∵,平面,平面,,
∴平面,
∴以点D为原点,以DA方向为x轴正方向,以DC方向为y轴正方向,以DE方向为z轴正方向,建立空间直角坐标系,如图,
则,
∴,
∵平面,
∴平面的一个法向量是,
设平面的法向量是,
则,即,令,则,
∴一个法向量,
∴
∴平面与平面所成的锐二面角的大小为
【考点】平面与平面垂直的判定;用空间向量求平面间的夹角
【解析】【分析】(1) 利用四边形为矩形,所以,再利用结合线线垂直证出线面垂直,所以平面,再利用线面垂直证出面面垂直,从而证出平面ADE平面ABCD。
(2)利用直线 平面结合线面垂直的定义证出线线垂直,所以,再利用结合线线垂直证出线面垂直,所以平面,所以以点D为原点,以DA方向为x轴正方向,以DC方向为y轴正方向,以DE方向为z轴正方向,建立空间直角坐标系,从而求出点的坐标,再结合向量的坐标表示求出向量的坐标,再结合数量积求向量夹角公式,进而求出平面ADE与平面BCF所成的锐二面角的大小。
21.【答案】(1)证明:因为底面是矩形,所以.
因为平面,所以,
.以为原点,,,
所在直线分别为轴、轴,轴,建立
如图所示的空间直角坐标系,
则(0,0,0),(1,0,0),(1,2,0),(0,2,0),(0,0,2),(0,1,1),
所以(1,2,0),(0,1,1),(1,0,2).
设平面的一个法向量为,
则,即
取,则,.
所以是平面的一个法向量.
因为,且平面,
所以//平面
(2)解:由(1)可知,,
又因为,所以平面.
所以(0,2,0)是平面的一个法向量.
设平面与平面的夹角为,
则
所以平面与平面夹角的余弦值为.
(3)解:因为为的中点,所以(,1,1),所以(,0,0).
又因为(1,2,2),所以,
所以与不垂直.
而平面,
所以棱上不存在点,使得平面.
【考点】向量语言表述线面的垂直、平行关系;用空间向量求平面间的夹角
【解析】【分析】(1)以为原点,,,所在直线分别为轴、轴,轴,建立空间直角坐标系, 求得平面ACE的一个法向量,由 证明出 //平面 ;
(2)易知 (0,2,0)是平面的一个法向量,设平面与平面的夹角为, 利用向量法即可求出平面与平面夹角的余弦值;
(3)求出的坐标,根据 ,判断出与不垂直,可得棱上不存在点,使得平面.
22.【答案】(1)证明:取 的中点为 ,连接 ,
因为 分别为 的中点,所以 ,
又因为 平面 ,且 ,
所以平面 平面 ,
又由 平面 ,所以 平面 .
(2)解:以 为原点, 所在的直线分别为 轴、 轴,以垂直平面 的直线为 轴,建立空间直角坐标系,如图所示,
因为底面 是边长为2的菱形,设 ,
在直角 中,可得 ,
在直角 中,可得 ,
在 中,因为 ,所以 ,
即 ,解得 ,
设 ,可得 ,
则 ,
设平面 的法向量为 ,则 ,
令 ,可得 ,
设直线 与平面 所成角为 ,
所以 ,解得 ,即 ,
所以存在点 ,且 的长为 .
【考点】直线与平面平行的判定;用空间向量求直线与平面的夹角
【解析】【分析】 (1)取 的中点为 ,连接 ,利用 分别为 的中点,再结合中点作中位线的方法和中位线的性质,所以 ,再利用线线平行证出线面平行,再结合线面平行证出面面平行,所以平面 平面 ,再结合面面平行的性质定理证出线面平行,从而证出直线 平面 。
(2) 以 为原点, 所在的直线分别为 轴、z轴,以垂直平面 的直线为 轴,建立空间直角坐标系, 从而求出点的坐标,再结合向量的坐标表示求出向量的坐标,再利用数量积求向量夹角公式得出直线 与平面 所成角的正弦值,再结合直线 与平面 所成角的正弦值为 ,从而得出点M的坐标,进而得出存在点 ,并求出此时对应的 的长。
25
