精讲精练·专项突破 第二章《直线与圆的方程》单元能力提升(含详细解析)
文档属性
| 名称 | 精讲精练·专项突破 第二章《直线与圆的方程》单元能力提升(含详细解析) |  | |
| 格式 | docx | ||
| 文件大小 | 119.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-18 16:28:06 | ||
图片预览




文档简介
精讲精练·专项突破
2021-2022学年高二上学期人教版(2019)
第二章 《直线与圆的方程》 单元能力提升(含详细解析)
一、单选题
1.(2021高一上·湖北月考)2018年5月至2019年春,在阿拉伯半岛和伊朗西南部,沙漠蝗虫迅速繁衍,呈指数增长,引发了蝗灾,到2020年春季蝗灾已波及印度和巴基斯坦,假设蝗虫的日增长率为5.2%,最初有只,则经过( )天能达到最初的1000倍(参考数据:,,,).
A.22 B.132 C.139 D.184
【答案】C
【考点】指数函数的实际应用;指数式与对数式的互化;对数的运算性质
【解析】【解答】设过天能达到最初的1000倍,
由已知条件得,即,
两边同取自然对数得,
解得,
则过139天能达到最初的1000倍.
故答案为:.
【分析】根据题意由已知条件即可得出函数的解析式,结合指对互化公式,由对数的运算性质计算出结果即可。
2.(2021高一下·会泽月考)下列不等式成立的是( )
A. B.
C. D.
【答案】A
【考点】指数函数的单调性与特殊点;对数函数的单调性与特殊点;正弦函数的单调性
【解析】【解答】 , , ,所以 .
故答案为:A.
【分析】根据题意由指数函数的单调性即可得出,由正弦函数的值域即可得出,由对数函数的单调性即可得出,从而比较出大小。
3.(2021高二上·湖南期末)设,,,则a,b,c的大小关系为( )
A. B. C. D.
【答案】D
【考点】指数函数的单调性与特殊点;对数函数的单调性与特殊点
【解析】【解答】,,则,
又,∴,
故答案为:D.
【分析】首先由指数函数的单调性即可求出a与b的大小关系,再由代数式的单调性求出a、b、c的大小关系,由此即可得出答案。
4.(2021高二下·鹤岗期末)已知幂函数 的图象过点 ,则 ( )
A.2 B.3 C.8 D.9
【答案】D
【考点】幂函数的概念、解析式、定义域、值域
【解析】【解答】解:设幂函数f(x)=xα,
则由题意得2α=4,解得α=2
则f(x)=x2
∴f(3)=32=9
故答案为:D
【分析】根据幂函数的概念求解即可.
5.(2021高一上·陈仓期中)已知函数 其中 且 的图象恒过定点A,若点A也在函数 的图象上,则 的值为( )
A. B. C. D.
【答案】A
【考点】有理数指数幂的运算性质;对数的运算性质;对数函数的图象与性质;对数函数的单调性与特殊点
【解析】【解答】解:对于函数 ,令x+3=1,即x=-2时,y=-1,则定点A(-2,-1),代入 ,得3-2+b=-1,解得,则 ,则.
故答案为:A
【分析】根据对数函数的图象与性质,结合指数运算性质与对数运算性质求解即可.
6.(2021高一上·焦作期中)已知 , , ,则( )
A. B. C. D.
【答案】A
【考点】指数函数的单调性与特殊点
【解析】【解答】 , , ,
又因为函数 在R上单调递增,
,
。
故答案为:A
【分析】利用已知条件结合指数函数单调性和对数函数的单调性,再结合与特殊值对应的指数与对数大小关系比较,从而比较出a,b,c的大小。
7.(2021高二上·杭州期末)已知函数 , , 的零点分别为a,b,c,下列各式正确的是( )
A. B. C. D.
【答案】D
【考点】指数函数的图象与性质;对数函数的图象与性质
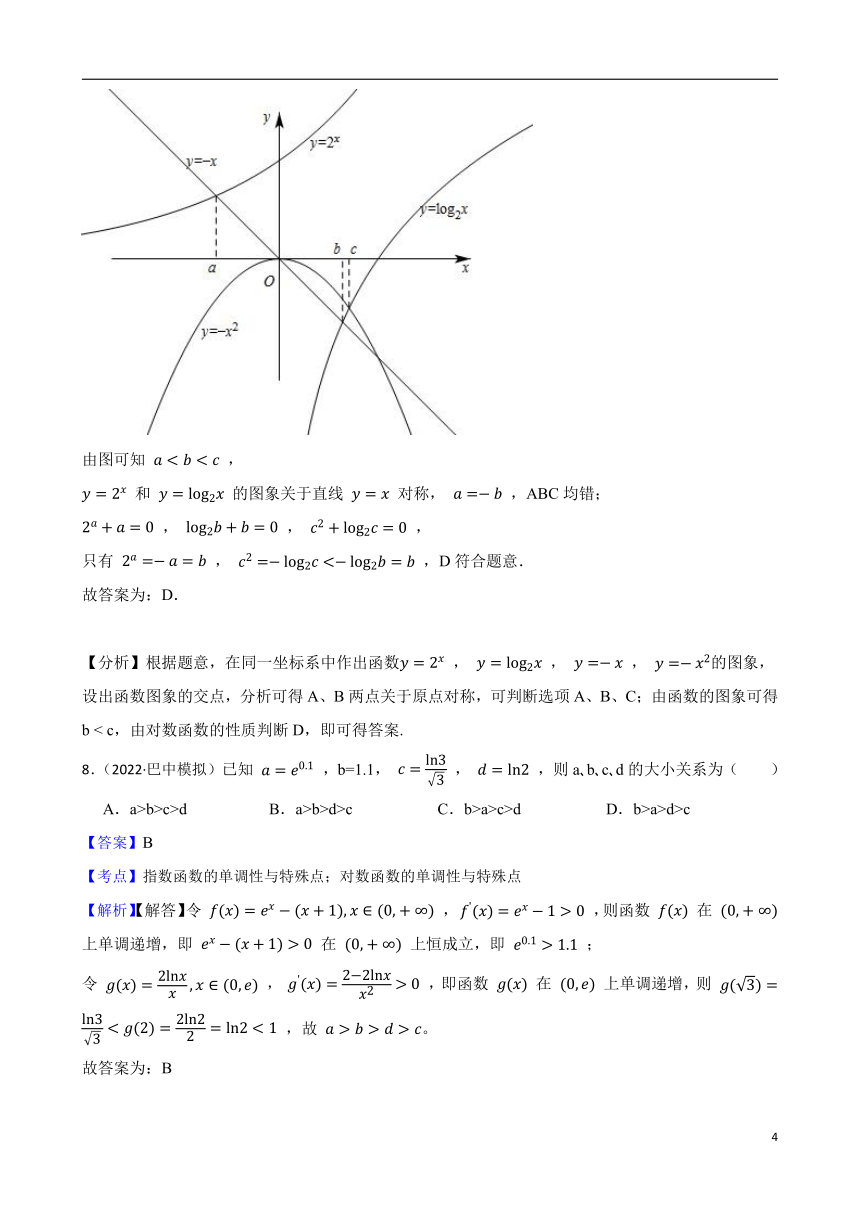
【解析】【解答】如图,作出函数 , , , 的图象,
由图可知 ,
和 的图象关于直线 对称, ,ABC均错;
, , ,
只有 , ,D符合题意.
故答案为:D.
【分析】根据题意,在同一坐标系中作出函数 , , , 的图象,设出函数图象的交点,分析可得A、B两点关于原点对称,可判断选项A、B、C;由函数的图象可得b < c,由对数函数的性质判断D,即可得答案.
8.(2022·巴中模拟)已知 ,b=1.1, , ,则a b c d的大小关系为( )
A.a>b>c>d B.a>b>d>c C.b>a>c>d D.b>a>d>c
【答案】B
【考点】指数函数的单调性与特殊点;对数函数的单调性与特殊点
【解析】【解答】令 , ,则函数 在 上单调递增,即 在 上恒成立,即 ;
令 , ,即函数 在 上单调递增,则 ,故 。
故答案为:B
【分析】令 ,再利用求导的方法判断函数的单调性,即 在 上恒成立,即 ,令 , 再利用求导的方法判断函数的单调性,从而找出a b c d的大小关系。
二、多选题
9.(2021高一上·电白期中)以下化简结果正确的是(字母均为正数)( )
A.
B.
C.
D.
【答案】B,D
【考点】有理数指数幂的化简求值
【解析】【解答】A选项: ,A选项错误;
B选项: ,B选项正确;
C选项: ,C选项错误;
D选项: ,D选项正确;
故答案为:BD.
【分析】利用已知条件结合指数幂的运算法则,从而化简求值,进而找出结果正确的选项。
10.(2021高一下·杭州期末)已知某湖泊蓝藻面积 (单位: )与时间 (单位:月)满足 .若第1个月的蓝藻面积为 ,则( )
A.蓝藻面积每个月的增长率为100%
B.蓝藻每个月增加的面积都相等
C.第6个月时,蓝藻面积就会超过
D.若蓝藻面积到 , , 所经过的时间分别是 , , ,则
【答案】A,C,D
【考点】对数的运算性质;对数函数、指数函数与幂函数的增长差异;函数模型的选择与应用
【解析】【解答】由题意可知,函数 图象经过 ,即 ,
,
,
,
蓝藻每个月的面积是上个月的2倍,
每个月的增长率为 ,故 选项正确,
,即每个月增长量为 ,非常数,故 选项错误,
当 时, ,故 选项正确,
若蓝藻面积到 , , 所经过的时间分别是 , , ,
,
, , ,
,故 选项正确.
故答案为:ACD.
【分析】由题意可知,函数 图象经过 ,再结合代入法求出a的值,从而求出指数函数的解析式,再利用增长率的求解方法结合指数与对数的互化公式和对数的运算法则,从而找出正确的选项。
11.(2021高三上·潍坊月考)设,,为正实数,且,则下列关系式可能成立的是( )
A. B. C. D.
【答案】A,C,D
【考点】幂函数的单调性、奇偶性及其应用
【解析】【解答】,
即
令
则,
当时,
当时,因为幂函数在上单调递增,
当时,因为幂函数在上单调递减,
.
故答案为:ACD.
【分析】 ,,为正实数,且,可得,令则,对k分类讨论,利用幂函数的单调性即可得出答案。
12.(2022高三上·汕尾期末)已知a,b都是不等于1的正实数,且a>b,0<1,则下列不等式一定成立的是( )
A. B.
C. D.
【答案】B,D
【考点】指数函数的单调性与特殊点;对数函数的单调性与特殊点;基本不等式在最值问题中的应用
【解析】【解答】函数,因为,所以是减函数,
因为a>b,所以,A不符合题意.
函数,因为,所以在是增函数,
因为a>b,所以,B符合题意.
函数,因为,所以在是减函数,
因为a>b,所以,C不符合题意.
,当且仅当时取等号,
又因为,所以,D符合题意.
故答案为:BD
【分析】利用已知条件结合指数函数的单调性和幂函数的单调性,再利用对数函数的单调性和均值不等式变形求最值的方法,从而找出不等式一定成立的选项。
三、填空题
13.(2021高一上·桂林月考)化简:2lg50+lg4(lg20+2lg5)+3(lg200)= .
【答案】10+5lg2+2lg2lg5
【考点】对数的运算性质
【解析】【解答】原式 .
故答案为:10+5lg2+2lg2lg5
【分析】由对数的运算性质整理化简计算出结果即可。
14.(2021高一上·肥城期中)已知幂函数 经过点 ,则 .
【答案】
【考点】函数解析式的求解及常用方法;幂函数的图象
【解析】【解答】设幂函数为 ,所以 。
故答案为: 。
【分析】利用已知条件结合代入法,从而求出幂函数的解析式。
15.(2021高三上·荔湾月考)把物体放在冷空气中冷却,如果物体原来的温度是 ℃,空气的温度是 ℃,则 后物体的温度 (单位:°C)可由公式 求得,其中 是一个随着物体与空气的接触状况而定的正常数,现有52°C的物体,放在12°C的空气中冷却,2min以后物体的温度是32°C,则再经过6min该物体的温度可冷却到 .
【答案】14.5℃
【考点】根据实际问题选择函数类型
【解析】【解答】依题意得,带入数据到 ,得到 ,整理得到 ,解得 ;那么6min后,即 时,
.
故答案为:14.5℃
【分析】 由冷却2min的数据计算出的值,再代入冷却6min的数据,进行运算即可.
16.(2021高三上·嫩江月考)已知函数 , ,则函数 的零点个数为 个.
【答案】10
【考点】有理数指数幂的运算性质;对数的运算性质;分段函数的应用;函数的零点
【解析】【解答】解:令h(x)=0得g(f(x))=1,
令g(x)=1得或
解得x=0或x=e或,
作出f(x)的函数图象如图所示:
由图象可知f(x)=0有4个解,f(x)=e有两个解, 有4个解,
故h(x)共有10个零点.
故答案为:10
【分析】根据分段函数的定义与性质,结合函数零点的概念以及指数运算与对数运算,运用数形结合思想求解即可.
四、解答题
17.(2021高一上·兰州期末)求值:
(1);
(2).
【答案】(1)解:
(2)解:
【考点】有理数指数幂的运算性质;对数的运算性质
【解析】【分析】(1)由指数幂的运算性质计算出结果即可。
(2)利用对数的运算性质,计算出结果即可。
18.(2022高一上·杭州期末)化简求值:
(1);
(2)已知,求的值.
【答案】(1)解:原式.
(2)解:原式.
【考点】有理数指数幂的运算性质;对数的运算性质;同角三角函数间的基本关系;诱导公式
【解析】【分析】 (1 )由题意利用指数、对数的运算性质,计算求得结果;
(2)由题意,利用诱导公式、同角三角函数的基本关系,计算求得结果.
19.某地区原有森林木材存量为a ,且每年增长率为25%.因生产建设的需要,每年年底要砍伐的木材量为b,设an为n年后该地区森林木材存量.
(1)求{an}的通项公式.
(2)为保护生态环境,防止水土流失,该地区每年的森林木材存量应不少于 a,如果b= a ,那么该地区今后会发生水土流失吗 若会,需要经过几年 (lg2≈0.30)
【答案】(1)解:设第一年后的森林木材存量为a1,第n年后的森林木材存量为an,
由上面的a1, a2,a3推测 (其中n∈N*).
证明如下:①当n=1时,a1= a-b,结论成立,
②假设当n=k时, 成立,
则当n=k +1时,
也就是说,当n=k+1时,结论也成立.
由①②可知, 对一切n∈N*成立.
(2)解:当 时,若该地区今后发生水土流失,则森林木材存量必须小于 a,
即 ,
两边取对数得 ,即
∴经过8年后该地区就会发生水土流失。
【考点】换底公式的应用;数列的概念及简单表示法;数学归纳法
【解析】【分析】(1)利用已知条件结合归纳推理的方法,进而推测出第n年后的森林木材存量,再结合数学归纳法,从而证明出 对一切n∈N*成立,进而求出数列{an}的通项公式 。
(2) 当 时,若该地区今后发生水土流失,则森林木材存量必须小于 a,得出 ,两边取对数得 ,再利用换底公式得出n的取值范围,进而求出经过8年后该地区就会发生水土流失。
20.(2020高二上·定远期末)如图,以两条互相垂直的公路所在直线分别为x轴,y轴建立平面直角坐标系,公路附近有一居民区EFG和一风景区,其中 单位:百米 , ,风景区的部分边界为曲线C,曲线C的方程为 ,拟在居民和风景区间辟出一个三角形区域EMN用于工作人员办公,点M,N分别在x轴和EF上,且MN与曲线C相切于P点.
(1)设P点的横坐标为t,写出 面积的函数表达式 ;
(2)当t为何值时, 面积最小?并求出最小面积.
【答案】(1)解:由已知可知 ,故直线MN的斜率为 ,
直线MN的方程为 ,
令 可得 , .
又 , ,
直线EF的方程为 ,
联立方程组 ,解得 , ,
,
(2)解: .
当 时, , 单调递减,当 时, , 单调递增.
当 时, 取得最小值 .
当 时, 面积最小,最小面积为
【考点】根据实际问题选择函数类型
【解析】【分析】(1)根据曲线切线方程的求法,得到切线MN的方程,与EF方程联立,得到点N的坐标,利用 得到函数关系式;
(2)通过导数求得的单调性,可知极小值点即为最小值点,从而求得最小面积。
21.(2021高一上·河南月考)某博物馆为了保护一件珍贵文物,需要在一种透明又密封的长方体玻璃保护罩内充入保护液体.该博物馆需要支付保护这件文物的总费用由两部分组成:①罩内该种液体的体积比保护罩的容积少0.5立方米,且每立方米液体费用为2000元;②需支付一定的保险费用,且支付的保险费用与保护罩容积成反比,当容积为4立方米时,支付的保险费用为18000元.(长方体保护罩最大容积为10立方米)
(1)求该博物馆需支付保护这件文物的总费用 与保护罩容积 之间的函数关系式;
(2)求该博物馆支付总费用的最小值,并求出此时长方体保护罩的容积.
【答案】(1)解:设保险费用为 ,代入 , ,解得 ,
则总费用 ,
即
(2)解:由基本不等式可得
,
当且仅当 立方米,在定义域范围内.
故当长方体保护罩容积为6立方米时,总费用最小值为23000元.
【考点】根据实际问题选择函数类型
【解析】【分析】 (1)根据支付的保险费用与保护罩容积成反比设出函数,求出比例系数,然后表示出总费用即可;
(2)利用均值不等式进行求解,注意等号成立的条件.
22.(2021·保定模拟)某生物研究者于元旦在湖中放入一些风眼莲(其覆盖面积为 ),这些风眼莲在湖中的蔓延速度越来越快,二月底测得凤眼莲的覆盖面积为 ,三月底测得凤眼莲的覆盖面积为 ,凤眼莲的覆盖面积 (单位: )与月份 (单位:月)的关系有两个函数模型 与 )可供选择.
(1)试判断哪个函数模型更合适并求出该模型的解析式;
(2)求凤眼莲的覆盖面积是元旦放入凤眼莲面积10倍以上的最小月份.(参考数据: , ).
【答案】(1)由题设可知,两个函数 、 )在 上均为增函数,
随着 的增大,函数 的值增加得越来越快,
而函数 的值增加得越来越慢,
由于风眼莲在湖中的蔓延速度越来越快,故而函数模型 满足要求.
由题意可得 ,解得 , ,
故该函数模型的解析式为 ;
(2)当 时, ,故元旦放入凤眼莲的面积为 ,
由 ,即 ,故 ,
由于 ,故 .
因此,凤眼莲覆盖面积是元旦放入凤眼莲面积10倍以上的最小月份是6月份.
【考点】根据实际问题选择函数类型
【解析】【分析】(1)函数 、 )在 上均为增函数,
随着x的增加,函数 的值增加的越来越快,而函数 的值增加得越来越慢,由题意可得 ,可得该模型的解析式;
(2)当 时, ,故元旦放入凤眼莲的面积为 , 得 ,解得即可求出凤眼莲覆盖面积是元旦放入凤眼莲面积10倍以上的最小月份。
14
2021-2022学年高二上学期人教版(2019)
第二章 《直线与圆的方程》 单元能力提升(含详细解析)
一、单选题
1.(2021高一上·湖北月考)2018年5月至2019年春,在阿拉伯半岛和伊朗西南部,沙漠蝗虫迅速繁衍,呈指数增长,引发了蝗灾,到2020年春季蝗灾已波及印度和巴基斯坦,假设蝗虫的日增长率为5.2%,最初有只,则经过( )天能达到最初的1000倍(参考数据:,,,).
A.22 B.132 C.139 D.184
【答案】C
【考点】指数函数的实际应用;指数式与对数式的互化;对数的运算性质
【解析】【解答】设过天能达到最初的1000倍,
由已知条件得,即,
两边同取自然对数得,
解得,
则过139天能达到最初的1000倍.
故答案为:.
【分析】根据题意由已知条件即可得出函数的解析式,结合指对互化公式,由对数的运算性质计算出结果即可。
2.(2021高一下·会泽月考)下列不等式成立的是( )
A. B.
C. D.
【答案】A
【考点】指数函数的单调性与特殊点;对数函数的单调性与特殊点;正弦函数的单调性
【解析】【解答】 , , ,所以 .
故答案为:A.
【分析】根据题意由指数函数的单调性即可得出,由正弦函数的值域即可得出,由对数函数的单调性即可得出,从而比较出大小。
3.(2021高二上·湖南期末)设,,,则a,b,c的大小关系为( )
A. B. C. D.
【答案】D
【考点】指数函数的单调性与特殊点;对数函数的单调性与特殊点
【解析】【解答】,,则,
又,∴,
故答案为:D.
【分析】首先由指数函数的单调性即可求出a与b的大小关系,再由代数式的单调性求出a、b、c的大小关系,由此即可得出答案。
4.(2021高二下·鹤岗期末)已知幂函数 的图象过点 ,则 ( )
A.2 B.3 C.8 D.9
【答案】D
【考点】幂函数的概念、解析式、定义域、值域
【解析】【解答】解:设幂函数f(x)=xα,
则由题意得2α=4,解得α=2
则f(x)=x2
∴f(3)=32=9
故答案为:D
【分析】根据幂函数的概念求解即可.
5.(2021高一上·陈仓期中)已知函数 其中 且 的图象恒过定点A,若点A也在函数 的图象上,则 的值为( )
A. B. C. D.
【答案】A
【考点】有理数指数幂的运算性质;对数的运算性质;对数函数的图象与性质;对数函数的单调性与特殊点
【解析】【解答】解:对于函数 ,令x+3=1,即x=-2时,y=-1,则定点A(-2,-1),代入 ,得3-2+b=-1,解得,则 ,则.
故答案为:A
【分析】根据对数函数的图象与性质,结合指数运算性质与对数运算性质求解即可.
6.(2021高一上·焦作期中)已知 , , ,则( )
A. B. C. D.
【答案】A
【考点】指数函数的单调性与特殊点
【解析】【解答】 , , ,
又因为函数 在R上单调递增,
,
。
故答案为:A
【分析】利用已知条件结合指数函数单调性和对数函数的单调性,再结合与特殊值对应的指数与对数大小关系比较,从而比较出a,b,c的大小。
7.(2021高二上·杭州期末)已知函数 , , 的零点分别为a,b,c,下列各式正确的是( )
A. B. C. D.
【答案】D
【考点】指数函数的图象与性质;对数函数的图象与性质
【解析】【解答】如图,作出函数 , , , 的图象,
由图可知 ,
和 的图象关于直线 对称, ,ABC均错;
, , ,
只有 , ,D符合题意.
故答案为:D.
【分析】根据题意,在同一坐标系中作出函数 , , , 的图象,设出函数图象的交点,分析可得A、B两点关于原点对称,可判断选项A、B、C;由函数的图象可得b < c,由对数函数的性质判断D,即可得答案.
8.(2022·巴中模拟)已知 ,b=1.1, , ,则a b c d的大小关系为( )
A.a>b>c>d B.a>b>d>c C.b>a>c>d D.b>a>d>c
【答案】B
【考点】指数函数的单调性与特殊点;对数函数的单调性与特殊点
【解析】【解答】令 , ,则函数 在 上单调递增,即 在 上恒成立,即 ;
令 , ,即函数 在 上单调递增,则 ,故 。
故答案为:B
【分析】令 ,再利用求导的方法判断函数的单调性,即 在 上恒成立,即 ,令 , 再利用求导的方法判断函数的单调性,从而找出a b c d的大小关系。
二、多选题
9.(2021高一上·电白期中)以下化简结果正确的是(字母均为正数)( )
A.
B.
C.
D.
【答案】B,D
【考点】有理数指数幂的化简求值
【解析】【解答】A选项: ,A选项错误;
B选项: ,B选项正确;
C选项: ,C选项错误;
D选项: ,D选项正确;
故答案为:BD.
【分析】利用已知条件结合指数幂的运算法则,从而化简求值,进而找出结果正确的选项。
10.(2021高一下·杭州期末)已知某湖泊蓝藻面积 (单位: )与时间 (单位:月)满足 .若第1个月的蓝藻面积为 ,则( )
A.蓝藻面积每个月的增长率为100%
B.蓝藻每个月增加的面积都相等
C.第6个月时,蓝藻面积就会超过
D.若蓝藻面积到 , , 所经过的时间分别是 , , ,则
【答案】A,C,D
【考点】对数的运算性质;对数函数、指数函数与幂函数的增长差异;函数模型的选择与应用
【解析】【解答】由题意可知,函数 图象经过 ,即 ,
,
,
,
蓝藻每个月的面积是上个月的2倍,
每个月的增长率为 ,故 选项正确,
,即每个月增长量为 ,非常数,故 选项错误,
当 时, ,故 选项正确,
若蓝藻面积到 , , 所经过的时间分别是 , , ,
,
, , ,
,故 选项正确.
故答案为:ACD.
【分析】由题意可知,函数 图象经过 ,再结合代入法求出a的值,从而求出指数函数的解析式,再利用增长率的求解方法结合指数与对数的互化公式和对数的运算法则,从而找出正确的选项。
11.(2021高三上·潍坊月考)设,,为正实数,且,则下列关系式可能成立的是( )
A. B. C. D.
【答案】A,C,D
【考点】幂函数的单调性、奇偶性及其应用
【解析】【解答】,
即
令
则,
当时,
当时,因为幂函数在上单调递增,
当时,因为幂函数在上单调递减,
.
故答案为:ACD.
【分析】 ,,为正实数,且,可得,令则,对k分类讨论,利用幂函数的单调性即可得出答案。
12.(2022高三上·汕尾期末)已知a,b都是不等于1的正实数,且a>b,0<1,则下列不等式一定成立的是( )
A. B.
C. D.
【答案】B,D
【考点】指数函数的单调性与特殊点;对数函数的单调性与特殊点;基本不等式在最值问题中的应用
【解析】【解答】函数,因为,所以是减函数,
因为a>b,所以,A不符合题意.
函数,因为,所以在是增函数,
因为a>b,所以,B符合题意.
函数,因为,所以在是减函数,
因为a>b,所以,C不符合题意.
,当且仅当时取等号,
又因为,所以,D符合题意.
故答案为:BD
【分析】利用已知条件结合指数函数的单调性和幂函数的单调性,再利用对数函数的单调性和均值不等式变形求最值的方法,从而找出不等式一定成立的选项。
三、填空题
13.(2021高一上·桂林月考)化简:2lg50+lg4(lg20+2lg5)+3(lg200)= .
【答案】10+5lg2+2lg2lg5
【考点】对数的运算性质
【解析】【解答】原式 .
故答案为:10+5lg2+2lg2lg5
【分析】由对数的运算性质整理化简计算出结果即可。
14.(2021高一上·肥城期中)已知幂函数 经过点 ,则 .
【答案】
【考点】函数解析式的求解及常用方法;幂函数的图象
【解析】【解答】设幂函数为 ,所以 。
故答案为: 。
【分析】利用已知条件结合代入法,从而求出幂函数的解析式。
15.(2021高三上·荔湾月考)把物体放在冷空气中冷却,如果物体原来的温度是 ℃,空气的温度是 ℃,则 后物体的温度 (单位:°C)可由公式 求得,其中 是一个随着物体与空气的接触状况而定的正常数,现有52°C的物体,放在12°C的空气中冷却,2min以后物体的温度是32°C,则再经过6min该物体的温度可冷却到 .
【答案】14.5℃
【考点】根据实际问题选择函数类型
【解析】【解答】依题意得,带入数据到 ,得到 ,整理得到 ,解得 ;那么6min后,即 时,
.
故答案为:14.5℃
【分析】 由冷却2min的数据计算出的值,再代入冷却6min的数据,进行运算即可.
16.(2021高三上·嫩江月考)已知函数 , ,则函数 的零点个数为 个.
【答案】10
【考点】有理数指数幂的运算性质;对数的运算性质;分段函数的应用;函数的零点
【解析】【解答】解:令h(x)=0得g(f(x))=1,
令g(x)=1得或
解得x=0或x=e或,
作出f(x)的函数图象如图所示:
由图象可知f(x)=0有4个解,f(x)=e有两个解, 有4个解,
故h(x)共有10个零点.
故答案为:10
【分析】根据分段函数的定义与性质,结合函数零点的概念以及指数运算与对数运算,运用数形结合思想求解即可.
四、解答题
17.(2021高一上·兰州期末)求值:
(1);
(2).
【答案】(1)解:
(2)解:
【考点】有理数指数幂的运算性质;对数的运算性质
【解析】【分析】(1)由指数幂的运算性质计算出结果即可。
(2)利用对数的运算性质,计算出结果即可。
18.(2022高一上·杭州期末)化简求值:
(1);
(2)已知,求的值.
【答案】(1)解:原式.
(2)解:原式.
【考点】有理数指数幂的运算性质;对数的运算性质;同角三角函数间的基本关系;诱导公式
【解析】【分析】 (1 )由题意利用指数、对数的运算性质,计算求得结果;
(2)由题意,利用诱导公式、同角三角函数的基本关系,计算求得结果.
19.某地区原有森林木材存量为a ,且每年增长率为25%.因生产建设的需要,每年年底要砍伐的木材量为b,设an为n年后该地区森林木材存量.
(1)求{an}的通项公式.
(2)为保护生态环境,防止水土流失,该地区每年的森林木材存量应不少于 a,如果b= a ,那么该地区今后会发生水土流失吗 若会,需要经过几年 (lg2≈0.30)
【答案】(1)解:设第一年后的森林木材存量为a1,第n年后的森林木材存量为an,
由上面的a1, a2,a3推测 (其中n∈N*).
证明如下:①当n=1时,a1= a-b,结论成立,
②假设当n=k时, 成立,
则当n=k +1时,
也就是说,当n=k+1时,结论也成立.
由①②可知, 对一切n∈N*成立.
(2)解:当 时,若该地区今后发生水土流失,则森林木材存量必须小于 a,
即 ,
两边取对数得 ,即
∴经过8年后该地区就会发生水土流失。
【考点】换底公式的应用;数列的概念及简单表示法;数学归纳法
【解析】【分析】(1)利用已知条件结合归纳推理的方法,进而推测出第n年后的森林木材存量,再结合数学归纳法,从而证明出 对一切n∈N*成立,进而求出数列{an}的通项公式 。
(2) 当 时,若该地区今后发生水土流失,则森林木材存量必须小于 a,得出 ,两边取对数得 ,再利用换底公式得出n的取值范围,进而求出经过8年后该地区就会发生水土流失。
20.(2020高二上·定远期末)如图,以两条互相垂直的公路所在直线分别为x轴,y轴建立平面直角坐标系,公路附近有一居民区EFG和一风景区,其中 单位:百米 , ,风景区的部分边界为曲线C,曲线C的方程为 ,拟在居民和风景区间辟出一个三角形区域EMN用于工作人员办公,点M,N分别在x轴和EF上,且MN与曲线C相切于P点.
(1)设P点的横坐标为t,写出 面积的函数表达式 ;
(2)当t为何值时, 面积最小?并求出最小面积.
【答案】(1)解:由已知可知 ,故直线MN的斜率为 ,
直线MN的方程为 ,
令 可得 , .
又 , ,
直线EF的方程为 ,
联立方程组 ,解得 , ,
,
(2)解: .
当 时, , 单调递减,当 时, , 单调递增.
当 时, 取得最小值 .
当 时, 面积最小,最小面积为
【考点】根据实际问题选择函数类型
【解析】【分析】(1)根据曲线切线方程的求法,得到切线MN的方程,与EF方程联立,得到点N的坐标,利用 得到函数关系式;
(2)通过导数求得的单调性,可知极小值点即为最小值点,从而求得最小面积。
21.(2021高一上·河南月考)某博物馆为了保护一件珍贵文物,需要在一种透明又密封的长方体玻璃保护罩内充入保护液体.该博物馆需要支付保护这件文物的总费用由两部分组成:①罩内该种液体的体积比保护罩的容积少0.5立方米,且每立方米液体费用为2000元;②需支付一定的保险费用,且支付的保险费用与保护罩容积成反比,当容积为4立方米时,支付的保险费用为18000元.(长方体保护罩最大容积为10立方米)
(1)求该博物馆需支付保护这件文物的总费用 与保护罩容积 之间的函数关系式;
(2)求该博物馆支付总费用的最小值,并求出此时长方体保护罩的容积.
【答案】(1)解:设保险费用为 ,代入 , ,解得 ,
则总费用 ,
即
(2)解:由基本不等式可得
,
当且仅当 立方米,在定义域范围内.
故当长方体保护罩容积为6立方米时,总费用最小值为23000元.
【考点】根据实际问题选择函数类型
【解析】【分析】 (1)根据支付的保险费用与保护罩容积成反比设出函数,求出比例系数,然后表示出总费用即可;
(2)利用均值不等式进行求解,注意等号成立的条件.
22.(2021·保定模拟)某生物研究者于元旦在湖中放入一些风眼莲(其覆盖面积为 ),这些风眼莲在湖中的蔓延速度越来越快,二月底测得凤眼莲的覆盖面积为 ,三月底测得凤眼莲的覆盖面积为 ,凤眼莲的覆盖面积 (单位: )与月份 (单位:月)的关系有两个函数模型 与 )可供选择.
(1)试判断哪个函数模型更合适并求出该模型的解析式;
(2)求凤眼莲的覆盖面积是元旦放入凤眼莲面积10倍以上的最小月份.(参考数据: , ).
【答案】(1)由题设可知,两个函数 、 )在 上均为增函数,
随着 的增大,函数 的值增加得越来越快,
而函数 的值增加得越来越慢,
由于风眼莲在湖中的蔓延速度越来越快,故而函数模型 满足要求.
由题意可得 ,解得 , ,
故该函数模型的解析式为 ;
(2)当 时, ,故元旦放入凤眼莲的面积为 ,
由 ,即 ,故 ,
由于 ,故 .
因此,凤眼莲覆盖面积是元旦放入凤眼莲面积10倍以上的最小月份是6月份.
【考点】根据实际问题选择函数类型
【解析】【分析】(1)函数 、 )在 上均为增函数,
随着x的增加,函数 的值增加的越来越快,而函数 的值增加得越来越慢,由题意可得 ,可得该模型的解析式;
(2)当 时, ,故元旦放入凤眼莲的面积为 , 得 ,解得即可求出凤眼莲覆盖面积是元旦放入凤眼莲面积10倍以上的最小月份。
14
