精讲精练·专项突破 第三章《圆锥曲线的方程》单元能力提升(含详细解析) (26)
文档属性
| 名称 | 精讲精练·专项突破 第三章《圆锥曲线的方程》单元能力提升(含详细解析) (26) |  | |
| 格式 | docx | ||
| 文件大小 | 121.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-18 16:28:06 | ||
图片预览




文档简介
精讲精练·专项突破
2021-2022学年高二上学期人教版(2019)
第三章 《圆锥曲线的方程》 单元能力提升(含详细解析)
一、单选题
1.(2021高三上·龙岩月考)牛顿曾经提出了常温环境下的温度冷却模型: ( 为时间,单位分钟, 为环境温度, 为物体初始温度, 为冷却后温度),假设一杯开水温度 ℃,环境温度 ℃,常数 ,大约经过多少分钟水温降为40℃?(结果保留整数,参考数据: )( )
A.9 B.8 C.7 D.6
【答案】C
【考点】对数函数图象与性质的综合应用;函数模型的选择与应用
【解析】【解答】由题意知: 分钟,
故答案为:C.
【分析】由已知条件即可得出函数的关系式,再由对数的运算性质计算出结果即可。
2.(2021高一下·江苏月考)函数 的零点所在区间是( )
A. B. C. D.
【答案】C
【考点】函数零点的判定定理
【解析】【解答】∵连续减函数 ,
∴f(3)=2﹣log23>0,f(4)= ﹣log24<0,
∴函数 的零点所在的区间是 (3,4)。
故答案为:C.
【分析】利用零点存在性定理,进而判断出函数零点所在的区间。
3.(2021·淄博零模)我们知道,人们对声音有不同的感觉,这与声音的强度有关系,声音的强度常用 (单位:瓦/米 ,即 )表示,但在实际测量时,声音的强度水平常用 (单位:分贝)表示,它们满足换算公式: ( ,其中 是人平均能听到的声音的最小强度),国家《城市区域噪声标准》中规定白天公共场所不超过60分贝,则要求声音的强度不超过( )
A. B.
C. D.
【答案】B
【考点】根据实际问题选择函数类型
【解析】【解答】令 ,可得 , .
故答案为:B.
【分析】令 ,可得 ,解得即可得出答案。
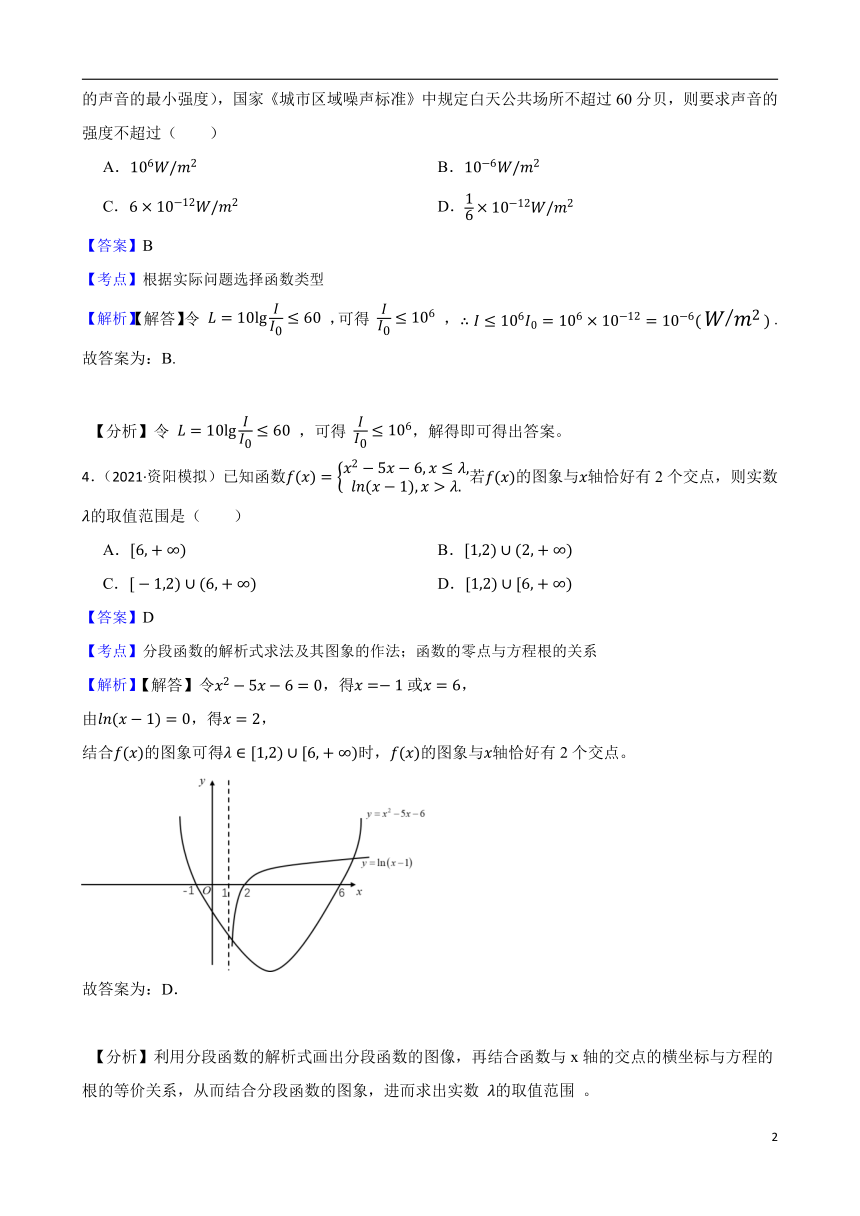
4.(2021·资阳模拟)已知函数若的图象与轴恰好有2个交点,则实数的取值范围是( )
A. B.
C. D.
【答案】D
【考点】分段函数的解析式求法及其图象的作法;函数的零点与方程根的关系
【解析】【解答】令,得或,
由,得,
结合的图象可得时,的图象与轴恰好有2个交点。
故答案为:D.
【分析】利用分段函数的解析式画出分段函数的图像,再结合函数与x轴的交点的横坐标与方程的根的等价关系,从而结合分段函数的图象,进而求出实数 的取值范围 。
5.(2021高三上·佛山月考)已知函数 存在两个零点,则正数 的取值范围是( )
A. B. C. D.
【答案】C
【考点】利用导数研究函数的单调性;函数的零点与方程根的关系
【解析】【解答】显然 , 有两个零点,即方程 , 在 上有两个解,
两边取对数得到 ,令 , , 在 单调递增,在 单调递减,
又当 时, ,当 时, ,
因为 有两个零点,则 ,
解得 .所以正数 的取值范围是 .
故答案为:C.
【分析】 函数存在两个零点可化为 在 上有两个解,构造函数,从而判断函数的性质,从而解得.
6.(2021高三上·南通月考)航天之父 俄罗斯科学家齐奥科夫斯基(K.E.Tsiolkovsky)于1903年给出火箭最大速度的计算公式 .其中, 是燃料相对于火箭的喷射速度, 是燃料的质量, 是火箭(除去燃料)的质量,v是火箭将燃料喷射完之后达到的速度.已知 ,则当火箭的最大速度 可达到 时,火箭的总质量(含燃料)至少是火箭(除去燃料)的质量的( )倍.
A. B. C. D.
【答案】A
【考点】函数模型的选择与应用
【解析】【解答】由题意可知: , ,
代入 可得 ,
所以 ,可得 ,
可得 ,即 ,
所以 ,
所以火箭的总质量(含燃料)的质量 是火箭(除去燃料)的质量 的 倍。
故答案为:A.
【分析】利用已知条件结合指数与对数的互化公式,从而求出火箭的总质量(含燃料)的质量 是火箭(除去燃料)的质量 的倍数。
7.(2021高三上·怀仁期中)已知函数 , 为奇函数,则下列叙述四个结论中正确的是( )
A.
B. 在 上存在零点,则a的最小值为
C. 在 上单调递增
D. 在 有且仅有一个极大值点
【答案】C
【考点】函数单调性的判断与证明;奇函数;函数在某点取得极值的条件;函数零点的判定定理
【解析】【解答】 ,所以
因为 是奇函数,所以 , ,解得: ,
因为 ,所以 ,解得: ,因为 ,所以 ,此时 , ,A选项错误;
,当 时,显然 , ,要想 存在零点,需要 ,解得: ,所以a的最小值为 ,B不符合题意;
,当 时, ,因为 在 单调递减,所以 在 单调递增,C选项正确;
,令 得: , ,当 时, ,令 得: , ,当 时, ,所以 在 上成立, 在 上成立,所以 在此区间上有一个极小值点,无极大值点,D不符合题意.
故答案为:C
【分析】利用已知条件结合导数的运算法则,进而求出其导函数,再结合辅助角公式得出,再利用函数 是奇函数,再结合奇函数的定义得出 , ,再利用 ,得出实数k的取值范围,再利用 ,从而得出实数k的值,进而求出此时 的值 ,再结合正切函数的定义,从而求出 的值;再利用已知条件结合零点存在性定理得出实数a的取值范围,进而求出实数a的最小值;再利用已知条件结合增函数的定义,从而判断出函数 在 上单调递增 ;利用已知条件结合求导的方法判断函数的单调性,进而求出函数 在 上有一个极小值点,无极大值点,进而找出结论正确的选项。
8.(2020高一上·天津期末)已知函数 , ,若对任意 ,总存在 ,使 ,则实数a的取值范围是( )
A. B.
C. D.
【答案】B
【考点】正弦函数的单调性;分段函数的应用
【解析】【解答】对任意 ,则 ,即函数 的值域为 ,
若对任意的 ,总存在 ,使 ,
设函数 的值域为 ,则满足 ,即可,
当 时,函数 为减函数,则此时 ,
当 时, ,
⑴当 ,即 时,满足条件 成立;
⑵当 时,此时 ,要使 成立,则此时当 时, ,所以 解得: ,
综上所述: 或 .
故答案为:B.
【分析】根据题意求出两个函数的值域,结合对任意x1∈[1,+∞),总存在x2∈R,使f(x1)=g(x2),将问题转化为f(x)的值域是g(x)值域的子集,对a 分情况讨论利用数形结合进行转化求解即可得出答案。
二、多选题
9.(2020高一上·德州期末)我们知道:函数 关于 对称的充要条件是 .某同学针对上述结论进行探究,得到一个真命题:函数 关于 对称的充要条件是 .若函数 满足 ,且当 时, ,则( )
A.
B.当 时,
C.函数 的零点为3,-1
D. 的解集为
【答案】B,D
【考点】必要条件、充分条件与充要条件的判断;函数解析式的求解及常用方法;函数单调性的性质;函数的零点
【解析】【解答】 ,则 关于 对称,所以 ,A不正确;
设 则 , ,B符合题意;
当 时,令 可得, ,所以函数零点为 ,C不正确;
,
当 时, ,所以
当 时, ,函数单调递减,可得 ,所以 或 ,D符合题意.
故答案为:BD
【分析】根据题意由函数图像对称的性质即可计算出函数的值,从而判断出选项A错误;由已知条件即可得出函数的解析式,从而判断出选项B正确;首先根据题意求出函数的零点,从而判断出选项C错误;根据题意由函数的单调性即可得到x的取值范围,由此判断出选项D正确,从而得出答案。
10.(2021高一上·辽宁月考)存在实数a使得函数有唯一零点,则实数m可以取值为( )
A. B.0 C. D.
【答案】A,B,C
【考点】函数单调性的性质;函数的零点与方程根的关系;函数的零点
【解析】【解答】函数有唯一零点,即方程有唯一根,
也就是与有唯一交点,
令,则,
由“对勾函数”的单调性可知,当,即时,有最小值2,
可得,即,
当时,符合题意,
当时,
则,解得且.
综上,实数的取值范围是,.
故答案为:ABC
【分析】根据题意由零点与方程的关系,即可得出与有唯一交点,结合对勾函数的单调性即可求出函数的最值,从而即可得出关于m的方程,再由二次方程的根的情况即可得出关于m的不等式,求解出m的取值范围即可。
11.(2021高一上·湖南月考)已知函数,则 ( )
A.若的最小值为-1,则
B.当时,恒成立
C.当时,存在且,使得
D.存在,使得对任意恒成立
【答案】A,C
【考点】分段函数的解析式求法及其图象的作法;不等式的综合;分段函数的应用
【解析】【解答】当时,.因为的最小值为,所以函数在上取最小值-1,则解得正确.
当时,令,解得,故当时,错误.
令,要满足,即只需函数的图象与函数的图象有交点即可,即将问题转化为将左侧的图象关于轴对称,与是否有交点,显然当开口特别大时,与存在交点,所以C符合题意.
当时,,显然不恒成立;当时,,因为,所以,即恒成立,则不恒成立,D不符合题意.
故答案为:AC
【分析】 根据题意由二次函数的图象和性质结合题意,即可求出a的取值,由此判断出选项A正确;由已知条件即可得出不等式,令结合一元二次不等式的解法,求解出x的取值范围,结合数形结合法由二次函数的图象和对数函数的图象,即可得出答案,由此判断出选项C;根据题意由已知条件即可得出不等式恒成立,结合二次函数的图象和性质即可求出函数的最值,结合题意即可求出关于a的不等式,求解出a的取值范围,由此判断出选项D错误,从而即可得出答案。
12.(2021高一上·湖南月考)已知函数和,下列结论中正确的有( )
A.若函数没有零点,则
B.若函数有2个零点,则
C.当时,函数有3个零点
D.若函数有6个零点,则
【答案】A,D
【考点】函数的零点与方程根的关系;函数的零点
【解析】【解答】没有零点,故,解得,A符合题意;
画出函数图像,如图所示,,即,故或,B不符合题意;
当时,,即或,,解得,当,无解,故共有1个零点,C不符合题意;
函数有6个零点,需满足的两个零点在上,即,,且,解得,D符合题意.
故答案为:AD.
【分析】由函数零点与方程根的关系,即可判断出选项A正确;由已知条件作出图象结合数形结合法,即可得出答案由此判断出选项B错误;结合函数零点与函数根的关系,即可判断出选项C错误;同理即可判断出选项D正确,从而即可得出答案。
三、填空题
13.(2020高一上·遂宁期末)设函数 ,则 = .
【答案】1
【考点】函数的值;分段函数的应用
【解析】【解答】因为函数 ,
所以 ,
所以 ,
所以 ,
故答案为:1
【分析】根据题意选择合适的函数解析式代入数值计算出结果即可。
14.(2020高一上·青岛期末)某种物资实行阶梯价格制度,具体见下表:
阶梯 年用量(千克) 价格(元/千克)
第一阶梯 不超过10的部分 6
第二阶梯 超过10而不超过20的部分 8
第三阶梯 超过20的部分 10
则一户居民使用该物资的年花费y(元)关于年用量x(千克)的函数关系式为 ;若某户居民使用该物资的年花费为100(元),则该户居民的年用量为 千克.
【答案】;15
【考点】分段函数的应用;函数模型的选择与应用
【解析】【解答】由表可得,当 时, ,
当 时, ,
当 时, ,
,
若某户居民使用该物资的年花费为100(元),
可得该户居民的年用量在 内,则 ,解得 ,
则该户居民的年用量为15千克。
故答案为: ;15。
【分析】利用某种物资实行阶梯价格制度表结合分类讨论的方法,进而求出一户居民使用该物资的年花费y(元)关于年用量x(千克)的函数关系式;再利用一户居民使用该物资的年花费y(元)关于年用量x(千克)的函数关系式结合已知条件,进而求出某户居民使用该物资的年花费为100(元)时该户居民的年用量。
15.(2020高三上·湖北期末)西气东输工程把西部的资源优势变为了经济优势,实现了气能源需求与供给的东西部衔接,同时该项工程的建设也加快了西部及沿线地区的经济发展.在输气管道工程建设过程中,某段直线形管道铺设需要经过一处平行峡谷,勘探人员在峡内恰好发现一处四分之一圆柱状的圆弧拐角,用测量仪器得到此横截圆面的圆心为 ,半径 且为 米,而运输人员利用运输工具水平横向移动直线形输气管不可避免的要经过此圆弧拐角,需从宽为38米的峡谷拐入宽为16米的峡谷.如图所示,位于峡谷悬崖壁上的两点 , 的连线恰好与圆弧拐角相切于点 (点 , , 在同一水平面内),若要使得直线形输气管能够顺利地通过圆弧拐角,其长度不能超过 米.
【答案】75
【考点】根据实际问题选择函数类型
【解析】【解答】设 ,其中 ,
延长OM,交AB于D,过B做SB垂线,交DO于G,延长ON,交AB于E,过A做SA垂线,交NO于F,如图所示:
在 中, ,AF=39,则 ,即 ,
在 中, , ,则 ,即 ,
在 中, ,OT=1,所以 ,
又 ,所以 ,
所以 = ,
因为 ,其中 ,当且仅当 时,等号成立,
所以
=
,
当且仅当 ,即 时等号成立,
所以若要使得直线形输气管能够顺利地通过圆弧拐角,其长度不能超过75米.
故答案为:75.
【分析】设 ,其中 ,则可得AB长度的表达式,利用凑“1”法,结合基本不等式,即可求得答案。
16.(2021高二上·丽水期末)已知函数 且 有两个不同的零点,则 的取值范围是
【答案】
【考点】函数恒成立问题;利用导数求闭区间上函数的最值;函数零点的判定定理
【解析】【解答】因为 ,则 ,
令 ,求导得 ,当 时, ,当 时, ,因此, 在 上单调递增,在 上单调递减, ,而当 时, 恒成立, ,
函数 有两个不同的零点当且仅当函数 的图象与直线 有两个公共点,
在同一坐标系内作出函数 的图象与直线 ,如图,
观察图象得:函数 的图象与直线 有两个公共点当且仅当 ,即 ,
于是得 或 ,
所以 的取值范围是 。
故答案为: 。
【分析】利用 ,则 ,令 ,再利用求导的方法判断函数的单调性,从而求出函数的最大值,当 时, 恒成立, ,再利用函数的零点与两函数的交点的横坐标的等价关系,所以函数 有两个不同的零点当且仅当函数 的图象与直线 有两个公共点,在同一坐标系内作出函数 的图象与直线 ,观察图象得出函数 的图象与直线 有两个公共点当且仅当 ,再利用代入法得出 ,再利用函数的单调性,得出实数的取值范围。
四、解答题
17.(2021高一上·费县期中)国家规定个人稿费纳税办法为:不超过800元的不纳税;超过800元而不超过4000元的按超出800元部分的14%纳税;超过4000元的按全部稿酬的11.2%纳税.
(1)写出纳税金额(元)关于稿费(元)的函数解析式;
(2)甲、乙两人同时各自出版了一本教学参考书,甲收到稿费并得知本次稿费收入需纳税420元,乙得知本次稿费收入恰好比甲多1200元,若乙本次稿费收入需纳税元,求的值.
【答案】(1)由题意可知,纳税金额(元)关于稿费(元)的函数解析式为
(2)若甲的稿费为4000元时,应纳税(元).
,∴甲的稿费应在800到4000之间,
设甲的稿费为元,,解得元.
因为乙本次稿费收入恰好比甲多1200元,所以乙的稿费收入为5000元,
所以(元).
【考点】分段函数的应用;函数模型的选择与应用
【解析】【分析】 (1)利用已知条件结合分段函数的模型,从而求出纳税金额(元)关于稿费(元)的函数解析式。
(2)利用已知条件结合分段函数的解析式,从而求出t的值。
18.已知
(1)画出f(x)的图象;
(2)若 ,求x的值;
(3)若 ,求x的取值范围.
【答案】(1)函数 的对称轴 ,当 时, ;
当 时, ;当 时, ,则f(x)的图象如图所示.
(2) 等价于 ①或 ②或 ③
解①得 ,②③的解集都为
∴当 时, .
(3)由于 ,结合此函数图象可知,
使 的x的取值范围是
【考点】分段函数的解析式求法及其图象的作法;分段函数的应用
【解析】【分析】(1)利用分段函数的解析式画出分段函数的图像。
(2)利用分段函数的图像求出满足要求 的x的值。
(3)利用分段函数的图像求出满足要求 的x的取值范围。
19.(2021高一上·焦作期中)某种商品原来每件价格为20元,年销售10万件.
(1)据市场调查,价格每提高1元,年销售量将相应减少2500件,要使该商品的年销售收入不低于原来的年销售收入,该商品每件价格最高为多少元?
(2)为了扩大该商品的影响力,提高年销售量,公司决定明年对该商品进行全面技术革新和营销策略改革,并提高价格到 元,公司拟投入 万元作为技术改革费用,投入140万元作为固定宣传费用,投入 万元作为浮动宣传费用.试问:该商品明年的销售量 (单位:万件)至少应达到多少万件,才可能使明年的销售收入不低于技术改革和宣传费用的总投入与原来的年销售收入之和?
【答案】(1)设每件定价为 元,依题意,有 ,
整理得 ,解得 .
因此要使销售的总收入不低于原收入,每件定价最多为40元.
(2)依题意, 时,不等式 能成立,
等价于 时, 有解.
∵ 时, (当且仅当 时,等号成立),
∴ .
因此当该商品明年的销售量 至少应达到12.2万件时,才可能使明年的销售收入不低于原收入与总投入之和,此时该商品的定价为每件30元.
【考点】一元二次不等式的解法;基本不等式在最值问题中的应用;函数模型的选择与应用
【解析】【分析】(1)利用已知条件结合一元二次不等式求解集的方法,从而求出要使销售的总收入不低于原收入,每件定价最多为40元。
(2) 依题意, 当 时,不等式 能成立,等价于 当 时, 有解,再利用均值不等式求最值的方法,进而得出实数a的取值范围,进而得出当该商品明年的销售量 至少应达到12.2万件时,才可能使明年的销售收入不低于原收入与总投入之和,此时该商品的定价为每件30元。
20.(2021高一上·大同期中)已知函数 .
(1)画出函数 的图象;
(2)当 ≥2时,求实数x的取值范围.
【答案】(1)由解析式知:
-2 -1 0 1 2 3
4 1 0 2 0 -2
∴ 的图象如下图示:
(2)由题可得: 或 ,解得 或 ,
∴实数x的取值范围为 .
【考点】分段函数的解析式求法及其图象的作法;分段函数的应用
【解析】【分析】(1)利用已知条件结合分段函数的解析式画出分段函数的图像。
(2)利用分段函数的图像结合解不等式组的方法,再结合并集的运算法则,从而求出满足不等式的实数x的取值范围。
21.判断函数 在区间 内的零点个数.
【答案】解: , 在 上恒成立, 在 上单调递增.
又 , ,则 在 内有且只有一个零点.
【考点】函数恒成立问题;利用导数研究函数的单调性;函数零点的判定定理
【解析】【分析】利用已知条件结合求导的方法判断函数的单调性,再结合不等式恒成立问题求解方法,再结合零点存在性定理,进而判断出函数 在区间 内的零点个数 。
22.(2021高一上·潍坊月考)已知定义在上的偶函数和奇函数满足.
(1)求函数和的解析式;
(2)设函数,当时,方程有解且所有解均在区间内,求实数,的取值范围.
【答案】(1)由,可得,
又是偶函数和是奇函数,故,
由,解得,
(2)由(1)得,
由,得,
∴,
由,即,化简得,即,解得,
∴,.
【考点】函数解析式的求解及常用方法;函数奇偶性的性质;函数的零点与方程根的关系
【解析】【分析】(1)利用已知条件结合奇函数和偶函数的定义,所以由,可得 , 再解方程组求出函数和的解析式。
(2) 由(1)结合 , 得出函数,由,得出,由,化简得出,再利用指数与对数的互化公式,解得x的取值范围,进而结合已知条件当时,方程有解且所有解均在区间内,从而求出实数,的取值范围。
18
2021-2022学年高二上学期人教版(2019)
第三章 《圆锥曲线的方程》 单元能力提升(含详细解析)
一、单选题
1.(2021高三上·龙岩月考)牛顿曾经提出了常温环境下的温度冷却模型: ( 为时间,单位分钟, 为环境温度, 为物体初始温度, 为冷却后温度),假设一杯开水温度 ℃,环境温度 ℃,常数 ,大约经过多少分钟水温降为40℃?(结果保留整数,参考数据: )( )
A.9 B.8 C.7 D.6
【答案】C
【考点】对数函数图象与性质的综合应用;函数模型的选择与应用
【解析】【解答】由题意知: 分钟,
故答案为:C.
【分析】由已知条件即可得出函数的关系式,再由对数的运算性质计算出结果即可。
2.(2021高一下·江苏月考)函数 的零点所在区间是( )
A. B. C. D.
【答案】C
【考点】函数零点的判定定理
【解析】【解答】∵连续减函数 ,
∴f(3)=2﹣log23>0,f(4)= ﹣log24<0,
∴函数 的零点所在的区间是 (3,4)。
故答案为:C.
【分析】利用零点存在性定理,进而判断出函数零点所在的区间。
3.(2021·淄博零模)我们知道,人们对声音有不同的感觉,这与声音的强度有关系,声音的强度常用 (单位:瓦/米 ,即 )表示,但在实际测量时,声音的强度水平常用 (单位:分贝)表示,它们满足换算公式: ( ,其中 是人平均能听到的声音的最小强度),国家《城市区域噪声标准》中规定白天公共场所不超过60分贝,则要求声音的强度不超过( )
A. B.
C. D.
【答案】B
【考点】根据实际问题选择函数类型
【解析】【解答】令 ,可得 , .
故答案为:B.
【分析】令 ,可得 ,解得即可得出答案。
4.(2021·资阳模拟)已知函数若的图象与轴恰好有2个交点,则实数的取值范围是( )
A. B.
C. D.
【答案】D
【考点】分段函数的解析式求法及其图象的作法;函数的零点与方程根的关系
【解析】【解答】令,得或,
由,得,
结合的图象可得时,的图象与轴恰好有2个交点。
故答案为:D.
【分析】利用分段函数的解析式画出分段函数的图像,再结合函数与x轴的交点的横坐标与方程的根的等价关系,从而结合分段函数的图象,进而求出实数 的取值范围 。
5.(2021高三上·佛山月考)已知函数 存在两个零点,则正数 的取值范围是( )
A. B. C. D.
【答案】C
【考点】利用导数研究函数的单调性;函数的零点与方程根的关系
【解析】【解答】显然 , 有两个零点,即方程 , 在 上有两个解,
两边取对数得到 ,令 , , 在 单调递增,在 单调递减,
又当 时, ,当 时, ,
因为 有两个零点,则 ,
解得 .所以正数 的取值范围是 .
故答案为:C.
【分析】 函数存在两个零点可化为 在 上有两个解,构造函数,从而判断函数的性质,从而解得.
6.(2021高三上·南通月考)航天之父 俄罗斯科学家齐奥科夫斯基(K.E.Tsiolkovsky)于1903年给出火箭最大速度的计算公式 .其中, 是燃料相对于火箭的喷射速度, 是燃料的质量, 是火箭(除去燃料)的质量,v是火箭将燃料喷射完之后达到的速度.已知 ,则当火箭的最大速度 可达到 时,火箭的总质量(含燃料)至少是火箭(除去燃料)的质量的( )倍.
A. B. C. D.
【答案】A
【考点】函数模型的选择与应用
【解析】【解答】由题意可知: , ,
代入 可得 ,
所以 ,可得 ,
可得 ,即 ,
所以 ,
所以火箭的总质量(含燃料)的质量 是火箭(除去燃料)的质量 的 倍。
故答案为:A.
【分析】利用已知条件结合指数与对数的互化公式,从而求出火箭的总质量(含燃料)的质量 是火箭(除去燃料)的质量 的倍数。
7.(2021高三上·怀仁期中)已知函数 , 为奇函数,则下列叙述四个结论中正确的是( )
A.
B. 在 上存在零点,则a的最小值为
C. 在 上单调递增
D. 在 有且仅有一个极大值点
【答案】C
【考点】函数单调性的判断与证明;奇函数;函数在某点取得极值的条件;函数零点的判定定理
【解析】【解答】 ,所以
因为 是奇函数,所以 , ,解得: ,
因为 ,所以 ,解得: ,因为 ,所以 ,此时 , ,A选项错误;
,当 时,显然 , ,要想 存在零点,需要 ,解得: ,所以a的最小值为 ,B不符合题意;
,当 时, ,因为 在 单调递减,所以 在 单调递增,C选项正确;
,令 得: , ,当 时, ,令 得: , ,当 时, ,所以 在 上成立, 在 上成立,所以 在此区间上有一个极小值点,无极大值点,D不符合题意.
故答案为:C
【分析】利用已知条件结合导数的运算法则,进而求出其导函数,再结合辅助角公式得出,再利用函数 是奇函数,再结合奇函数的定义得出 , ,再利用 ,得出实数k的取值范围,再利用 ,从而得出实数k的值,进而求出此时 的值 ,再结合正切函数的定义,从而求出 的值;再利用已知条件结合零点存在性定理得出实数a的取值范围,进而求出实数a的最小值;再利用已知条件结合增函数的定义,从而判断出函数 在 上单调递增 ;利用已知条件结合求导的方法判断函数的单调性,进而求出函数 在 上有一个极小值点,无极大值点,进而找出结论正确的选项。
8.(2020高一上·天津期末)已知函数 , ,若对任意 ,总存在 ,使 ,则实数a的取值范围是( )
A. B.
C. D.
【答案】B
【考点】正弦函数的单调性;分段函数的应用
【解析】【解答】对任意 ,则 ,即函数 的值域为 ,
若对任意的 ,总存在 ,使 ,
设函数 的值域为 ,则满足 ,即可,
当 时,函数 为减函数,则此时 ,
当 时, ,
⑴当 ,即 时,满足条件 成立;
⑵当 时,此时 ,要使 成立,则此时当 时, ,所以 解得: ,
综上所述: 或 .
故答案为:B.
【分析】根据题意求出两个函数的值域,结合对任意x1∈[1,+∞),总存在x2∈R,使f(x1)=g(x2),将问题转化为f(x)的值域是g(x)值域的子集,对a 分情况讨论利用数形结合进行转化求解即可得出答案。
二、多选题
9.(2020高一上·德州期末)我们知道:函数 关于 对称的充要条件是 .某同学针对上述结论进行探究,得到一个真命题:函数 关于 对称的充要条件是 .若函数 满足 ,且当 时, ,则( )
A.
B.当 时,
C.函数 的零点为3,-1
D. 的解集为
【答案】B,D
【考点】必要条件、充分条件与充要条件的判断;函数解析式的求解及常用方法;函数单调性的性质;函数的零点
【解析】【解答】 ,则 关于 对称,所以 ,A不正确;
设 则 , ,B符合题意;
当 时,令 可得, ,所以函数零点为 ,C不正确;
,
当 时, ,所以
当 时, ,函数单调递减,可得 ,所以 或 ,D符合题意.
故答案为:BD
【分析】根据题意由函数图像对称的性质即可计算出函数的值,从而判断出选项A错误;由已知条件即可得出函数的解析式,从而判断出选项B正确;首先根据题意求出函数的零点,从而判断出选项C错误;根据题意由函数的单调性即可得到x的取值范围,由此判断出选项D正确,从而得出答案。
10.(2021高一上·辽宁月考)存在实数a使得函数有唯一零点,则实数m可以取值为( )
A. B.0 C. D.
【答案】A,B,C
【考点】函数单调性的性质;函数的零点与方程根的关系;函数的零点
【解析】【解答】函数有唯一零点,即方程有唯一根,
也就是与有唯一交点,
令,则,
由“对勾函数”的单调性可知,当,即时,有最小值2,
可得,即,
当时,符合题意,
当时,
则,解得且.
综上,实数的取值范围是,.
故答案为:ABC
【分析】根据题意由零点与方程的关系,即可得出与有唯一交点,结合对勾函数的单调性即可求出函数的最值,从而即可得出关于m的方程,再由二次方程的根的情况即可得出关于m的不等式,求解出m的取值范围即可。
11.(2021高一上·湖南月考)已知函数,则 ( )
A.若的最小值为-1,则
B.当时,恒成立
C.当时,存在且,使得
D.存在,使得对任意恒成立
【答案】A,C
【考点】分段函数的解析式求法及其图象的作法;不等式的综合;分段函数的应用
【解析】【解答】当时,.因为的最小值为,所以函数在上取最小值-1,则解得正确.
当时,令,解得,故当时,错误.
令,要满足,即只需函数的图象与函数的图象有交点即可,即将问题转化为将左侧的图象关于轴对称,与是否有交点,显然当开口特别大时,与存在交点,所以C符合题意.
当时,,显然不恒成立;当时,,因为,所以,即恒成立,则不恒成立,D不符合题意.
故答案为:AC
【分析】 根据题意由二次函数的图象和性质结合题意,即可求出a的取值,由此判断出选项A正确;由已知条件即可得出不等式,令结合一元二次不等式的解法,求解出x的取值范围,结合数形结合法由二次函数的图象和对数函数的图象,即可得出答案,由此判断出选项C;根据题意由已知条件即可得出不等式恒成立,结合二次函数的图象和性质即可求出函数的最值,结合题意即可求出关于a的不等式,求解出a的取值范围,由此判断出选项D错误,从而即可得出答案。
12.(2021高一上·湖南月考)已知函数和,下列结论中正确的有( )
A.若函数没有零点,则
B.若函数有2个零点,则
C.当时,函数有3个零点
D.若函数有6个零点,则
【答案】A,D
【考点】函数的零点与方程根的关系;函数的零点
【解析】【解答】没有零点,故,解得,A符合题意;
画出函数图像,如图所示,,即,故或,B不符合题意;
当时,,即或,,解得,当,无解,故共有1个零点,C不符合题意;
函数有6个零点,需满足的两个零点在上,即,,且,解得,D符合题意.
故答案为:AD.
【分析】由函数零点与方程根的关系,即可判断出选项A正确;由已知条件作出图象结合数形结合法,即可得出答案由此判断出选项B错误;结合函数零点与函数根的关系,即可判断出选项C错误;同理即可判断出选项D正确,从而即可得出答案。
三、填空题
13.(2020高一上·遂宁期末)设函数 ,则 = .
【答案】1
【考点】函数的值;分段函数的应用
【解析】【解答】因为函数 ,
所以 ,
所以 ,
所以 ,
故答案为:1
【分析】根据题意选择合适的函数解析式代入数值计算出结果即可。
14.(2020高一上·青岛期末)某种物资实行阶梯价格制度,具体见下表:
阶梯 年用量(千克) 价格(元/千克)
第一阶梯 不超过10的部分 6
第二阶梯 超过10而不超过20的部分 8
第三阶梯 超过20的部分 10
则一户居民使用该物资的年花费y(元)关于年用量x(千克)的函数关系式为 ;若某户居民使用该物资的年花费为100(元),则该户居民的年用量为 千克.
【答案】;15
【考点】分段函数的应用;函数模型的选择与应用
【解析】【解答】由表可得,当 时, ,
当 时, ,
当 时, ,
,
若某户居民使用该物资的年花费为100(元),
可得该户居民的年用量在 内,则 ,解得 ,
则该户居民的年用量为15千克。
故答案为: ;15。
【分析】利用某种物资实行阶梯价格制度表结合分类讨论的方法,进而求出一户居民使用该物资的年花费y(元)关于年用量x(千克)的函数关系式;再利用一户居民使用该物资的年花费y(元)关于年用量x(千克)的函数关系式结合已知条件,进而求出某户居民使用该物资的年花费为100(元)时该户居民的年用量。
15.(2020高三上·湖北期末)西气东输工程把西部的资源优势变为了经济优势,实现了气能源需求与供给的东西部衔接,同时该项工程的建设也加快了西部及沿线地区的经济发展.在输气管道工程建设过程中,某段直线形管道铺设需要经过一处平行峡谷,勘探人员在峡内恰好发现一处四分之一圆柱状的圆弧拐角,用测量仪器得到此横截圆面的圆心为 ,半径 且为 米,而运输人员利用运输工具水平横向移动直线形输气管不可避免的要经过此圆弧拐角,需从宽为38米的峡谷拐入宽为16米的峡谷.如图所示,位于峡谷悬崖壁上的两点 , 的连线恰好与圆弧拐角相切于点 (点 , , 在同一水平面内),若要使得直线形输气管能够顺利地通过圆弧拐角,其长度不能超过 米.
【答案】75
【考点】根据实际问题选择函数类型
【解析】【解答】设 ,其中 ,
延长OM,交AB于D,过B做SB垂线,交DO于G,延长ON,交AB于E,过A做SA垂线,交NO于F,如图所示:
在 中, ,AF=39,则 ,即 ,
在 中, , ,则 ,即 ,
在 中, ,OT=1,所以 ,
又 ,所以 ,
所以 = ,
因为 ,其中 ,当且仅当 时,等号成立,
所以
=
,
当且仅当 ,即 时等号成立,
所以若要使得直线形输气管能够顺利地通过圆弧拐角,其长度不能超过75米.
故答案为:75.
【分析】设 ,其中 ,则可得AB长度的表达式,利用凑“1”法,结合基本不等式,即可求得答案。
16.(2021高二上·丽水期末)已知函数 且 有两个不同的零点,则 的取值范围是
【答案】
【考点】函数恒成立问题;利用导数求闭区间上函数的最值;函数零点的判定定理
【解析】【解答】因为 ,则 ,
令 ,求导得 ,当 时, ,当 时, ,因此, 在 上单调递增,在 上单调递减, ,而当 时, 恒成立, ,
函数 有两个不同的零点当且仅当函数 的图象与直线 有两个公共点,
在同一坐标系内作出函数 的图象与直线 ,如图,
观察图象得:函数 的图象与直线 有两个公共点当且仅当 ,即 ,
于是得 或 ,
所以 的取值范围是 。
故答案为: 。
【分析】利用 ,则 ,令 ,再利用求导的方法判断函数的单调性,从而求出函数的最大值,当 时, 恒成立, ,再利用函数的零点与两函数的交点的横坐标的等价关系,所以函数 有两个不同的零点当且仅当函数 的图象与直线 有两个公共点,在同一坐标系内作出函数 的图象与直线 ,观察图象得出函数 的图象与直线 有两个公共点当且仅当 ,再利用代入法得出 ,再利用函数的单调性,得出实数的取值范围。
四、解答题
17.(2021高一上·费县期中)国家规定个人稿费纳税办法为:不超过800元的不纳税;超过800元而不超过4000元的按超出800元部分的14%纳税;超过4000元的按全部稿酬的11.2%纳税.
(1)写出纳税金额(元)关于稿费(元)的函数解析式;
(2)甲、乙两人同时各自出版了一本教学参考书,甲收到稿费并得知本次稿费收入需纳税420元,乙得知本次稿费收入恰好比甲多1200元,若乙本次稿费收入需纳税元,求的值.
【答案】(1)由题意可知,纳税金额(元)关于稿费(元)的函数解析式为
(2)若甲的稿费为4000元时,应纳税(元).
,∴甲的稿费应在800到4000之间,
设甲的稿费为元,,解得元.
因为乙本次稿费收入恰好比甲多1200元,所以乙的稿费收入为5000元,
所以(元).
【考点】分段函数的应用;函数模型的选择与应用
【解析】【分析】 (1)利用已知条件结合分段函数的模型,从而求出纳税金额(元)关于稿费(元)的函数解析式。
(2)利用已知条件结合分段函数的解析式,从而求出t的值。
18.已知
(1)画出f(x)的图象;
(2)若 ,求x的值;
(3)若 ,求x的取值范围.
【答案】(1)函数 的对称轴 ,当 时, ;
当 时, ;当 时, ,则f(x)的图象如图所示.
(2) 等价于 ①或 ②或 ③
解①得 ,②③的解集都为
∴当 时, .
(3)由于 ,结合此函数图象可知,
使 的x的取值范围是
【考点】分段函数的解析式求法及其图象的作法;分段函数的应用
【解析】【分析】(1)利用分段函数的解析式画出分段函数的图像。
(2)利用分段函数的图像求出满足要求 的x的值。
(3)利用分段函数的图像求出满足要求 的x的取值范围。
19.(2021高一上·焦作期中)某种商品原来每件价格为20元,年销售10万件.
(1)据市场调查,价格每提高1元,年销售量将相应减少2500件,要使该商品的年销售收入不低于原来的年销售收入,该商品每件价格最高为多少元?
(2)为了扩大该商品的影响力,提高年销售量,公司决定明年对该商品进行全面技术革新和营销策略改革,并提高价格到 元,公司拟投入 万元作为技术改革费用,投入140万元作为固定宣传费用,投入 万元作为浮动宣传费用.试问:该商品明年的销售量 (单位:万件)至少应达到多少万件,才可能使明年的销售收入不低于技术改革和宣传费用的总投入与原来的年销售收入之和?
【答案】(1)设每件定价为 元,依题意,有 ,
整理得 ,解得 .
因此要使销售的总收入不低于原收入,每件定价最多为40元.
(2)依题意, 时,不等式 能成立,
等价于 时, 有解.
∵ 时, (当且仅当 时,等号成立),
∴ .
因此当该商品明年的销售量 至少应达到12.2万件时,才可能使明年的销售收入不低于原收入与总投入之和,此时该商品的定价为每件30元.
【考点】一元二次不等式的解法;基本不等式在最值问题中的应用;函数模型的选择与应用
【解析】【分析】(1)利用已知条件结合一元二次不等式求解集的方法,从而求出要使销售的总收入不低于原收入,每件定价最多为40元。
(2) 依题意, 当 时,不等式 能成立,等价于 当 时, 有解,再利用均值不等式求最值的方法,进而得出实数a的取值范围,进而得出当该商品明年的销售量 至少应达到12.2万件时,才可能使明年的销售收入不低于原收入与总投入之和,此时该商品的定价为每件30元。
20.(2021高一上·大同期中)已知函数 .
(1)画出函数 的图象;
(2)当 ≥2时,求实数x的取值范围.
【答案】(1)由解析式知:
-2 -1 0 1 2 3
4 1 0 2 0 -2
∴ 的图象如下图示:
(2)由题可得: 或 ,解得 或 ,
∴实数x的取值范围为 .
【考点】分段函数的解析式求法及其图象的作法;分段函数的应用
【解析】【分析】(1)利用已知条件结合分段函数的解析式画出分段函数的图像。
(2)利用分段函数的图像结合解不等式组的方法,再结合并集的运算法则,从而求出满足不等式的实数x的取值范围。
21.判断函数 在区间 内的零点个数.
【答案】解: , 在 上恒成立, 在 上单调递增.
又 , ,则 在 内有且只有一个零点.
【考点】函数恒成立问题;利用导数研究函数的单调性;函数零点的判定定理
【解析】【分析】利用已知条件结合求导的方法判断函数的单调性,再结合不等式恒成立问题求解方法,再结合零点存在性定理,进而判断出函数 在区间 内的零点个数 。
22.(2021高一上·潍坊月考)已知定义在上的偶函数和奇函数满足.
(1)求函数和的解析式;
(2)设函数,当时,方程有解且所有解均在区间内,求实数,的取值范围.
【答案】(1)由,可得,
又是偶函数和是奇函数,故,
由,解得,
(2)由(1)得,
由,得,
∴,
由,即,化简得,即,解得,
∴,.
【考点】函数解析式的求解及常用方法;函数奇偶性的性质;函数的零点与方程根的关系
【解析】【分析】(1)利用已知条件结合奇函数和偶函数的定义,所以由,可得 , 再解方程组求出函数和的解析式。
(2) 由(1)结合 , 得出函数,由,得出,由,化简得出,再利用指数与对数的互化公式,解得x的取值范围,进而结合已知条件当时,方程有解且所有解均在区间内,从而求出实数,的取值范围。
18
