精讲精练·专项突破 第三章《圆锥曲线的方程》单元能力提升(含详细解析) (30)
文档属性
| 名称 | 精讲精练·专项突破 第三章《圆锥曲线的方程》单元能力提升(含详细解析) (30) |  | |
| 格式 | docx | ||
| 文件大小 | 107.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-18 16:28:06 | ||
图片预览




文档简介
精讲精练·专项突破
2021-2022学年高二上学期人教版(2019)
第三章 《圆锥曲线的方程》 单元能力提升(含详细解析)
一、单选题
1.(2020高一上·蓬江期末) 表示不超过x的最大整数,例如, .若 是函数 的零点,则 ( )
A.1 B.2 C.3 D.4
【答案】B
【考点】函数零点的判定定理
【解析】【解答】因为函数 在定义域 上连续的增函数,
且 ,
又∵ 是函数 的零点,
∴ ,
所以 ,
故答案为:B.
【分析】 可判断函数f (x)在定义域(0, +∞)上连续,且是增函数,从而由零点判定定理求解.
2.(2021高一上·桂林月考)已知12是函数 的一个零点,则 的值是( )
A.1 B.0 C.2 D. +1
【答案】B
【考点】函数的值;分段函数的应用;函数的零点
【解析】【解答】由题意知: ,可得 ,
∴ ,则 .
∴ .
故答案为:B
【分析】由已知条件结合零点的定义代入到函数的解析式,由对数的运算性质整理即可得出m的取值,从而得到函数的解析式,再把数值代入计算出结果即可。
3.(2022高一上·温州期末)已知函数,若在定义域上恒成立,则的值是( )
A.-1 B.0 C.1 D.2
【答案】C
【考点】函数恒成立问题;函数的零点与方程根的关系
【解析】【解答】由题设,定义域为,
令,可得或,
∴在上,在上,
若,
∴要使在定义域上恒成立,则在上,在上,
∴或也是的零点,则:
,无解;,可得;,无解;
∴。
故答案为:C.
【分析】利用已知条件结合函数的定义域和不等式恒成立问题求解方法,再结合函数零点求解方法,进而得出 的值 。
4.(2021·富平模拟)若函数 满足 ,且 时, ,已知函数 则函数 在区间 内的零点个数为( )
A.14 B.13 C.12 D.11
【答案】C
【考点】指数函数的图象与性质;对数函数的图象与性质;分段函数的应用;函数的零点
【解析】【解答】解:因为 ,所以函数 是周期为2函数,
因为 时, ,所以作出它的图象,则 的图象如图所示:(注意拓展它的区间)
再作出函数 的图象,
容易得出到交点为12个.
故答案为:C.
【分析】由已知条件结合周期公式即可得出函数的周期值,结合对数函数和指数函数的图象,再由题意作出函数的图象,利用零点的定义由数形结合法即可得出答案。
5.(2021·大庆模拟)把物体放在冷空气中冷却,如果物体原来的温度是 ,空气的温度是 , 分钟后物体的温度 可由公式 求得. 把温度是 的物体,放在 的空气中冷却 分钟后,物体的温度是 ,则 约为( )( )
A.1.69 B.2.89 C.4.58 D.6.61
【答案】B
【考点】函数模型的选择与应用
【解析】【解答】由题意 , , , ,
故答案为:B.
【分析】利用实际问题的已知条件结合公式 ,再利用代入法和指数与对数的互化公式,进而求出t约为的值。
6.(2022·昆明模拟)某商用无人机公司从2016年1月份开始投产,已知前4个月的产量分别为1万台,1.2万台,1.3万台,1.35万台,由于产品技术先进、质量可靠,前几个月的产品销售情况良好,为了方便营销人员在推销产品时,接受订单不至于过多或过少,需要估测后几个月的产量,通过模拟多个函数模型,发现模拟函数比较接近客观实际,用该函数模型估计第5个月的产量是(单位:万台)( )
A.1.37 B.1.375 C.1.38 D.1.385
【答案】B
【考点】函数模型的选择与应用
【解析】【解答】对于函数模型,将前三个月产量的坐标代入,有,
解得,,,则,
当时,,与实际产量相符,
即由前4个月产量可得函数,
所以当时,。
故答案为:B
【分析】利用函数模型,将前三个月产量的坐标代入,从而解方程组求出a,b,c的值,进而求出函数的解析式,再利用代入法得出当时,,与实际产量相符,从而由前4个月产量可得函数,再利用赋值法估计出第5个月的产量。
7.(2022·永州模拟)在流行病学中,基本传染数是指每名感染者平均可传染的人数.假设某种传染病的基本传染数为,1个感染者在每个传染期会接触到个新人,这个人中有个人接种过疫苗(称为接种率),那么1个感染者传染人数为.已知某种传染病在某地的基本传染数,为了使1个感染者传染人数不超过1,则该地疫苗的接种率至少为( )
A.45% B.55% C.65% D.75%
【答案】D
【考点】函数模型的选择与应用
【解析】【解答】为了使得1个感染者传染人数不超过1,只需,即,
因为,故,可得。
故答案为:D.
【分析】利用已知条件得出,再利用结合代入法,从而解不等式得出的取值范围,进而得出该地疫苗的接种率至少的百分数。
8.(2021高三上·五华月考)设 是定义域为 的奇函数,且 ,当 时, , .将函数 的正零点从小到大排序,则 的第4个正零点为( )
A. B. C. D.
【答案】C
【考点】函数奇偶性的性质;奇偶函数图象的对称性;函数的零点
【解析】【解答】解:∵ 是定义域为 的奇函数,
∴f(0)=0
由 知f(x)关于直线x=1对称,则f(2)=f(0)=0,
即f(2)=1+b=0,则b=-1,
又 ,则f(1)=3,即a-1-1=3,解得
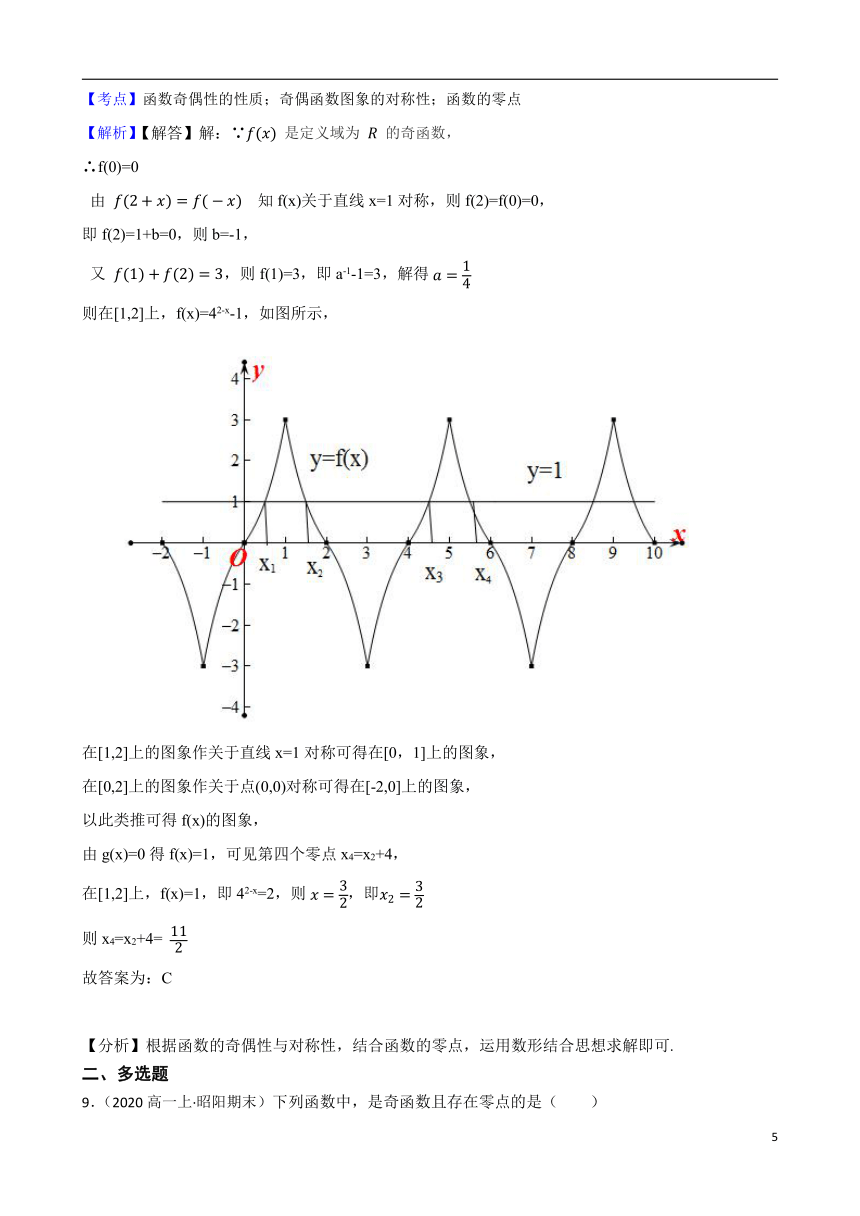
则在[1,2]上,f(x)=42-x-1,如图所示,
在[1,2]上的图象作关于直线x=1对称可得在[0,1]上的图象,
在[0,2]上的图象作关于点(0,0)对称可得在[-2,0]上的图象,
以此类推可得f(x)的图象,
由g(x)=0得f(x)=1,可见第四个零点x4=x2+4,
在[1,2]上,f(x)=1,即42-x=2,则,即
则x4=x2+4=
故答案为:C
【分析】根据函数的奇偶性与对称性,结合函数的零点,运用数形结合思想求解即可.
二、多选题
9.(2020高一上·昭阳期末)下列函数中,是奇函数且存在零点的是( )
A.y=x3+x B.y=log2x C.y=2x2-3 D.y=x|x|
【答案】A,D
【考点】函数奇偶性的判断;函数零点的判定定理
【解析】【解答】A中,y=x3+x为奇函数,且存在零点x=0,与题意相符;
B中,y=log2x定义域不关于原点对称,故其为非奇非偶函数,与题意不符;
C中,y=2x2-3为偶函数,与题意不符;
D中,y=x|x|是奇函数,且存在零点x=0,与题意相符.
故答案为:AD.
【分析】利用已知条件结合奇函数的定义和零点存在性定理,从而找出是奇函数且存在零点的函数。
10.(2020高一上·肇庆期末)下列说法中正确的是( )
A.函数 只有一个零点,且该零点在区间 上
B.若 是定义在 上的奇函数, ,且当 时, ,则
C.已知 的定义域为 ,且 为奇函数, 为偶函数,则 一定是奇函数
D.实数 是命题“ ”为假命题的充分不必要条件
【答案】B,C,D
【考点】必要条件、充分条件与充要条件的判断;奇函数;函数奇偶性的判断;函数零点的判定定理
【解析】【解答】函数 在 上单调递增,又 ,
所以该零点在区间 上,A不符合题意;
由 得, ,
又 是定义在 上的奇函数,所以 ,
当 时, ,所以 ,
故 ,所以 ,B符合题意;
由 为奇函数,得 ,
由 为偶函数,得 ,
所以 ,
所以函数 的周期为8,故 ,所以 一定是奇函数,C符合题意;
命题“ ”为假命题,则“ ”为真命题,
当 时,“ ”为真命题,
当 时,由 可得
所以命题“ ”为假命题的充要条件是
故实数 是命题“ ”为假命题的充分不必要条件,D符合题意.
故答案为:BCD
【分析】利用已知条件结合零点存在性定理、奇函数的定义、奇函数和偶函数的定义判断函数奇偶性的方法、充分条件、必要条件的判断方法,进而找出说法正确的选项。
11.(2021高一上·靖远期末)设函数,则( )
A.当时,的值域为
B.当的单调递增区间为时,
C.当时,函数有2个零点
D.当时,关于x的方程有3个实数解
【答案】A,B,D
【考点】函数的值域;函数单调性的性质;根的存在性及根的个数判断;函数的零点
【解析】【解答】对A,当时,若x>1,,若x≤1,,于是的值域为,A符合题意;
的单调递增区间是和,因为的单调递增区间是,所以,即,B符合题意;
当时,由,得,当时,令,得.此方程有唯一解,得,即,C不符合题意;
当时,如图所示,
的图象与直线有3个交点,D符合题意.
故答案为:ABD.
【分析】由a的取值即可得出函数的解析式,然后由指数函数和二次函数的性质即可求出函数的值域,由此判断出选项A正确;结合指数函数和二次函数的单调性即可得出函数的单调性,由此即可求出a的取值范围,由此判断出选项B正确;由零点和方程根的关系即可求出a的取值范围,由此即可判断出选项C错误;利用数形结合法即可求出,当时 方程解的个数,由此即可判断出选项D正确,从而即可得出答案。
12.(2022·莆田模拟)已知定义在上的函数( )
A.若恰有两个零点,则的取值范围是
B.若恰有两个零点,则的取值范围是
C.若的最大值为,则的取值个数最多为2
D.若的最大值为,则的取值个数最多为3
【答案】A,C
【考点】三角函数的最值;函数零点的判定定理
【解析】【解答】令,
若恰有两个零点,则有:,
解得的取值范围是:,
若的最大值为,分两种情况讨论:
①当,即时,根据正弦函数的单调性可知,,
解得:
②当,即时,根据正弦函数的单调性可知,在上单调递增
则有:,
结合函数与在上的图象可知,如下图:
故存在唯一的,使得,
综上可知,若的最大值为,则的取值个数最多为2。
故答案为:AC
【分析】令,若恰有两个零点结合零点存在性定理,得出实数的取值范围,若的最大值为,再利用分类讨论的方法,①当,得出时,再根据正弦函数的单调性求出函数的最大值,进而求出的值;②当,得出时,再根据正弦函数的单调性可知函数在上的单调性,进而求出函数得知最大值,即,再结合函数与在上的图象可知,得出存在唯一的,使得,进而得出若的最大值为时的实数的取值最多的个数,从而找出正确的选项。
三、填空题
13.若二次函数 的两个零点分别是2和3,则 的值为 .
【答案】-4
【考点】一元二次方程的解集及其根与系数的关系;函数的零点与方程根的关系
【解析】【解答】因为二次函数 的两个零点分别是2和3,
所以一元二次方程 的两个根分别是2和3,
由一元二次方程根与系数关系得: ,解得 ,
因此, 。
故答案为:-4。
【分析】利用函数的零点与方程的根的等价关系,因为二次函数 的两个零点分别是2和3,所以一元二次方程 的两个根分别是2和3,再利用韦达定理求出a,b的值,从而求出2a+b的值。
14.(2020高一上·沈阳期末)已知函数 则不等式 的解集是 .
【答案】{x|x≤1}
【考点】分段函数的应用
【解析】【解答】∵函数 ,
∴当x-1≥0,即 时, ,故 ;
当 ,即 时, ,故 ;
∴不等式 的解集是:{x|x≤1}.
故答案为:{x|x≤1}.
【分析】分x-1≥0和两种情况代入对应的解析式求解,即可求得不等式 的解集。
15.(2020高一上·天津期末)若f(x)= 是定义在R上的减函数,则a的取值范围是 .
【答案】
【考点】函数单调性的性质;分段函数的应用
【解析】【解答】由题意知, ,
解得 ,所以 .
故答案为:
【分析】由题意结合一次函数的单调性:一次项系数大于零为增函数,一次项系数小于零为减函数;即可得到关于a的不等式组求解出a的取值范围即可。
16.(2021高二下·湖北开学考)已知函数 (其中e为无理数且 )在 上有两个零点,且 使 成立,则实数a的取值范围为 .
【答案】 且
【考点】利用导数研究函数的单调性;函数的零点与方程根的关系
【解析】【解答】由函数 在 上有两个零点,即方程 在 上有两个解,
即方程 在 上有不等于2的根,
令 ,则 ,
所以函数 在 上为单调递增函数,
所以 且 ,
又由 使 成立,即 使得 成立,
即 使 ,即 使 成立,
函数 在 上为单调递增函数,所以 ,
综上可知,实数a的取值范围为 且 。
故答案为: 且 。
【分析】由函数 在 上有两个零点,再结合函数的零点与方程的根的等价关系,即方程 在 上有两个解,即方程 在 上有不等于2的根,令 ,再利用求导的方法判断函数的单调性,所以函数 在 上为单调递增函数,所以 且 ,又由 使 成立,即 使得 成立,即 使 成立,再利用函数 在 上的单调性,所以 ,从而求出实数a的取值范围。
四、解答题
17.(2020高一上·吉林期末)某沙漠原来面积为 ,经过绿化改造,每年沙漠面积的减少率为 ,当沙漠面积到原来面积的一半时,所用时间是 年,已知到2020年年末,沙漠剩余面积为原来面积的
(1)求
(2)到2020年年末,该沙漠已改造了多少年?
【答案】(1)解:由题意,可得 ,整理得 .
(2)解:设经过 年剩余面积为原来的 ,可得 ,
所以 ,
由(1)知 ,即 ,可得 ,解得 .
答:到2020年年末,该沙漠已改造了5年.
【考点】函数模型的选择与应用
【解析】【分析】(1)利用已知条件建立函数模型,从而求出p的值。
(2)利用已知条件建立函数模型,再利用(1)的结论结合指数幂的运算法则,从而求出到2020年年末,该沙漠已改造了的年数。
18.(2020高三上·兴宁期末)小明在某物流派送公司找到了一份派送员的工作,该公司给出了两种日薪薪酬方案.甲方案:底薪100元,每派送一单奖励1元;乙方案:底薪140元,每日前54单没有奖励,超过54单的部分每单奖励20元.
(1)请分别求出甲、乙两种薪酬方案中日薪y(单位:元)与送货单数n的函数关系式;
(2)根据该公司所有派送员100天的派送记录,发现派送员的日平均派送单数满足以下条件:在这100天中的派送量指标满足如图所示的直方图,其中当某天的派送量指标在 时,日平均派送量为 单.若将频率视为概率,回答下列问题:
①估计这100天中的派送量指标的平均数(同一组中的数据用该组区间的中点值作代表) ;
②根据以上数据,设每名派送员的日薪为 (单位:元),试分别求出甲、乙两种方案的日薪 的分布列及数学期望. 请利用数学期望帮助小明分析他选择哪种薪酬方案比较合适?并说明你的理由.
【答案】(1)解:甲: ,乙: ,故为
,
(2)解:①读图可知,20个0.1,30个0.3,20个0.5,20个0.7,10个0.9,故平均数
②甲:
P(概率) 0.2 0.3 0.2 0.2 0.1
X(日薪) 152 154 156 158 160
EX=
乙:
P(概率) 0.2 0.3 0.2 0.2 0.1
X(日薪) 140 140 180 220 260
EX=
乙的期望更高,故答案为:择乙方案.
【考点】根据实际问题选择函数类型
【解析】【分析】(1)根据题意,列出解析式即可;
(2) ① 分别计算出每个区间中点值的个数,然后乘以总数,求和,除以个数,即可得到平均值 ② 分别计算出每个指标下薪资待遇,计算期望,比较大小做出选择。
19.(2021·河北模拟)已知函数 .
(1)从① ,② 这两个条件中选择一个,求 零点的个数;
(2)若 ,讨论函数 的单调性.
注:若第(1)问选择两个条件分别解答,则按第一个解答计分.
【答案】(1)选①,当 时, , ,
令 ,
则 ,所以 在 上是单调递增函数,
设 为 的根,
由 , ,
所以 ,
当 时 , 单调递减,
当 时 , 单调递增,
所以 在 处有最小值, ,且 ,
所以 ,
因为 ,所以 ,
因为 , ,
此时 有2个零点;
选②,当 时, , ,
令 ,
则 ,所以 在 上是单调递增函数,
在 上是单调递减函数,
在 有最大值 ,所以 , 是单调递增函数,
因为 , ,
所以 , 在 单调且连续,所以存在 使得 ,
即零点的个数为1.
(2)若 , ,令 ,
所以 ,
令 ,得 或 ,
当 时,
(i) 时, , 单调递增,
(ii) 时, , 单调递减,
(iii) 时, , 单调递增,
当 时,
由 时, , 单调递增,
当 时,
(i) 或 时, , 单调递增,
(ii) 时, , 单调递减.
【考点】利用导数研究函数的单调性;函数零点的判定定理
【解析】【分析】 (1)若选①:求出f(x), h(x)= f' (x),利用导数判断h (x )的单调性,结合函数零点的存在性定理,即可判断f (x )零点的个数;
若选②:求出f(x),令h(x)= f' (x),利用导数判断h (x )的单调性,结合函数零点的存在性定理,即可判断f (x )零点的个数;
(2)令函数g(x)= xf(x),求出g' (x)= 0的根,分 , , 三种情况,判断导函数的正负,从而得到函数的单调性.
20.(2021高一上·青岛期中)某科研单位在研发某种合金产品的过程中发现了一种新型合金材料,由大数据分析得到该产品的性能指标值y(y值越大产品性能越好)与这种新型合金材料的含量x(单位:克)的关系:当 时,y是x的二次函数;当 时, .测得的部分数据如下表所示:
x 0 2 4 12 …
y -4 4 4 …
(1)求y关于x的函数解析式;
(2)求该新型合金材料的含量x为何值时产品性能达到最佳.
【答案】(1)当 时,y是x的二次函数,设 ,
由 , 可得 ,
由 , 可得 ①,
由 , 可得 ②,
由①②得 , ,
即
当 时, ,
由 , ,可得 ,即
综上,
(2)1°当 时, ,
所以当 时,y取得最大值5
2°当 时, 单调递减,所以当 时,y取得最大值4
综上所述,当该新型合金材料的含量为3时产品性能达到最佳.
【考点】函数解析式的求解及常用方法;分段函数的解析式求法及其图象的作法;函数的最值及其几何意义;分段函数的应用
【解析】【分析】(1)根据题意由特殊值代入法计算出a与b的值,从而得到函数的解析式。
(2)由已知条件把实际问题转化为数学问题,结合题意由二次函数和指数函数的性质即可求出函数的最值。
21.(2021·嘉定模拟)数学建模小组检测到相距3米的A,B两光源的强度分别为a,b,异于A,B的线段 上任意一点C处的光强度y等于两光源到该处的强度之和,设 米.
(1)假设某处的光强度与光源的强度成正比,与到光源的距离的平方成反比,比例系数为常数 ,测得数据:当 时, ;当 时, ,求A,B两处的光强度,并写出函数 的解析式;
(2)假设某处的光强度与光源的强度成正比,与到光源的距离成反比,比例系数为常数 ,测得数据:当 时, ;当 时, ,问何处的光强度最弱?并求最弱处的光强度.
【答案】(1)解:由已知,得
所以 , ,故 ,
(2)解:由已知,得 ,所以 ,
故 , .
因为 ,
当且仅当
所以当 时的C处,光强度最弱为
【考点】基本不等式在最值问题中的应用;函数模型的选择与应用
【解析】【分析】(1) 由已知,得 ,再利用当 时, ;当 时, ,从而结合代入法解方程组求出a,b的值,进而求出函数的解析式。
(2) 由已知,得 ,再利用当 时, ;当 时, ,从而结合代入法解方程组求出a,b的值,进而求出函数的解析式为 , ,
因为 ,再结合均值不等式求最值的方法,从而求出当 时的C处,光强度最弱为 。
22.(2021高一上·深圳竞赛)将连续正整数1,2,……,n (n∈N*)从小到大排列构成一个数123……*n,F(n)为这个数的位数(如n=12时,此数为123456 789 101 112,共有15个数字,F(12)=15),现从这个数中随机取一个数字,p(n)为恰好取到0的概率.
(1)求p(100);
(2)令g(n)为这个数中数字0的个数,f(n)为这个数中数字9的个数,h(n)= f(n)-g(n),S={n|h(n)=1,n≤100,n∈N*},求当n∈S时p(n)的最大值.
【答案】(1)解:当 n=100时,这个数中总共有192个数字,其中数字0的个数为11,所以恰好取到0的概率为p(100)= -
(2)当n=b(1≤b≤9,b∈N), g(n)=0;
当n=10k+b(1≤k≤9, 0≤b≤9, k∈N*, b∈N)时,g(n)=k;
当n=100时,g(n)=11, 即g(n)=
同理有f(n)=
由h(n)= f(n)-g(n)=1,可知n=9,19, 29,39, 49,59,69, 79,89,90,
所以当n≤100时,S={9,19, 29,39,49,59,69, 79,89,90}.
当n=9时,P(9)=0
当n=90时,p(90)=
当n=10k+9(1≤k≤8,k∈N*)时,p(n)=
由y= 关于k单调递增,故当n=10k+9(1≤k≤8, k∈N *)时,p(n)的最大值为p(89)=
又 <
所以当n∈S时,p(n)的最大为 -
【考点】分段函数的解析式求法及其图象的作法;古典概型及其概率计算公式;分段函数的应用
【解析】【分析】(1)根据古典概型概率计算公式求解即可;
(2)根据分段函数的定义,结合题意分别求得函数g(n),f(n),再根据h(n)= f(n)-g(n)=1,结合古典概型概率计算公式,利用分类讨论思想求解即可.
18
2021-2022学年高二上学期人教版(2019)
第三章 《圆锥曲线的方程》 单元能力提升(含详细解析)
一、单选题
1.(2020高一上·蓬江期末) 表示不超过x的最大整数,例如, .若 是函数 的零点,则 ( )
A.1 B.2 C.3 D.4
【答案】B
【考点】函数零点的判定定理
【解析】【解答】因为函数 在定义域 上连续的增函数,
且 ,
又∵ 是函数 的零点,
∴ ,
所以 ,
故答案为:B.
【分析】 可判断函数f (x)在定义域(0, +∞)上连续,且是增函数,从而由零点判定定理求解.
2.(2021高一上·桂林月考)已知12是函数 的一个零点,则 的值是( )
A.1 B.0 C.2 D. +1
【答案】B
【考点】函数的值;分段函数的应用;函数的零点
【解析】【解答】由题意知: ,可得 ,
∴ ,则 .
∴ .
故答案为:B
【分析】由已知条件结合零点的定义代入到函数的解析式,由对数的运算性质整理即可得出m的取值,从而得到函数的解析式,再把数值代入计算出结果即可。
3.(2022高一上·温州期末)已知函数,若在定义域上恒成立,则的值是( )
A.-1 B.0 C.1 D.2
【答案】C
【考点】函数恒成立问题;函数的零点与方程根的关系
【解析】【解答】由题设,定义域为,
令,可得或,
∴在上,在上,
若,
∴要使在定义域上恒成立,则在上,在上,
∴或也是的零点,则:
,无解;,可得;,无解;
∴。
故答案为:C.
【分析】利用已知条件结合函数的定义域和不等式恒成立问题求解方法,再结合函数零点求解方法,进而得出 的值 。
4.(2021·富平模拟)若函数 满足 ,且 时, ,已知函数 则函数 在区间 内的零点个数为( )
A.14 B.13 C.12 D.11
【答案】C
【考点】指数函数的图象与性质;对数函数的图象与性质;分段函数的应用;函数的零点
【解析】【解答】解:因为 ,所以函数 是周期为2函数,
因为 时, ,所以作出它的图象,则 的图象如图所示:(注意拓展它的区间)
再作出函数 的图象,
容易得出到交点为12个.
故答案为:C.
【分析】由已知条件结合周期公式即可得出函数的周期值,结合对数函数和指数函数的图象,再由题意作出函数的图象,利用零点的定义由数形结合法即可得出答案。
5.(2021·大庆模拟)把物体放在冷空气中冷却,如果物体原来的温度是 ,空气的温度是 , 分钟后物体的温度 可由公式 求得. 把温度是 的物体,放在 的空气中冷却 分钟后,物体的温度是 ,则 约为( )( )
A.1.69 B.2.89 C.4.58 D.6.61
【答案】B
【考点】函数模型的选择与应用
【解析】【解答】由题意 , , , ,
故答案为:B.
【分析】利用实际问题的已知条件结合公式 ,再利用代入法和指数与对数的互化公式,进而求出t约为的值。
6.(2022·昆明模拟)某商用无人机公司从2016年1月份开始投产,已知前4个月的产量分别为1万台,1.2万台,1.3万台,1.35万台,由于产品技术先进、质量可靠,前几个月的产品销售情况良好,为了方便营销人员在推销产品时,接受订单不至于过多或过少,需要估测后几个月的产量,通过模拟多个函数模型,发现模拟函数比较接近客观实际,用该函数模型估计第5个月的产量是(单位:万台)( )
A.1.37 B.1.375 C.1.38 D.1.385
【答案】B
【考点】函数模型的选择与应用
【解析】【解答】对于函数模型,将前三个月产量的坐标代入,有,
解得,,,则,
当时,,与实际产量相符,
即由前4个月产量可得函数,
所以当时,。
故答案为:B
【分析】利用函数模型,将前三个月产量的坐标代入,从而解方程组求出a,b,c的值,进而求出函数的解析式,再利用代入法得出当时,,与实际产量相符,从而由前4个月产量可得函数,再利用赋值法估计出第5个月的产量。
7.(2022·永州模拟)在流行病学中,基本传染数是指每名感染者平均可传染的人数.假设某种传染病的基本传染数为,1个感染者在每个传染期会接触到个新人,这个人中有个人接种过疫苗(称为接种率),那么1个感染者传染人数为.已知某种传染病在某地的基本传染数,为了使1个感染者传染人数不超过1,则该地疫苗的接种率至少为( )
A.45% B.55% C.65% D.75%
【答案】D
【考点】函数模型的选择与应用
【解析】【解答】为了使得1个感染者传染人数不超过1,只需,即,
因为,故,可得。
故答案为:D.
【分析】利用已知条件得出,再利用结合代入法,从而解不等式得出的取值范围,进而得出该地疫苗的接种率至少的百分数。
8.(2021高三上·五华月考)设 是定义域为 的奇函数,且 ,当 时, , .将函数 的正零点从小到大排序,则 的第4个正零点为( )
A. B. C. D.
【答案】C
【考点】函数奇偶性的性质;奇偶函数图象的对称性;函数的零点
【解析】【解答】解:∵ 是定义域为 的奇函数,
∴f(0)=0
由 知f(x)关于直线x=1对称,则f(2)=f(0)=0,
即f(2)=1+b=0,则b=-1,
又 ,则f(1)=3,即a-1-1=3,解得
则在[1,2]上,f(x)=42-x-1,如图所示,
在[1,2]上的图象作关于直线x=1对称可得在[0,1]上的图象,
在[0,2]上的图象作关于点(0,0)对称可得在[-2,0]上的图象,
以此类推可得f(x)的图象,
由g(x)=0得f(x)=1,可见第四个零点x4=x2+4,
在[1,2]上,f(x)=1,即42-x=2,则,即
则x4=x2+4=
故答案为:C
【分析】根据函数的奇偶性与对称性,结合函数的零点,运用数形结合思想求解即可.
二、多选题
9.(2020高一上·昭阳期末)下列函数中,是奇函数且存在零点的是( )
A.y=x3+x B.y=log2x C.y=2x2-3 D.y=x|x|
【答案】A,D
【考点】函数奇偶性的判断;函数零点的判定定理
【解析】【解答】A中,y=x3+x为奇函数,且存在零点x=0,与题意相符;
B中,y=log2x定义域不关于原点对称,故其为非奇非偶函数,与题意不符;
C中,y=2x2-3为偶函数,与题意不符;
D中,y=x|x|是奇函数,且存在零点x=0,与题意相符.
故答案为:AD.
【分析】利用已知条件结合奇函数的定义和零点存在性定理,从而找出是奇函数且存在零点的函数。
10.(2020高一上·肇庆期末)下列说法中正确的是( )
A.函数 只有一个零点,且该零点在区间 上
B.若 是定义在 上的奇函数, ,且当 时, ,则
C.已知 的定义域为 ,且 为奇函数, 为偶函数,则 一定是奇函数
D.实数 是命题“ ”为假命题的充分不必要条件
【答案】B,C,D
【考点】必要条件、充分条件与充要条件的判断;奇函数;函数奇偶性的判断;函数零点的判定定理
【解析】【解答】函数 在 上单调递增,又 ,
所以该零点在区间 上,A不符合题意;
由 得, ,
又 是定义在 上的奇函数,所以 ,
当 时, ,所以 ,
故 ,所以 ,B符合题意;
由 为奇函数,得 ,
由 为偶函数,得 ,
所以 ,
所以函数 的周期为8,故 ,所以 一定是奇函数,C符合题意;
命题“ ”为假命题,则“ ”为真命题,
当 时,“ ”为真命题,
当 时,由 可得
所以命题“ ”为假命题的充要条件是
故实数 是命题“ ”为假命题的充分不必要条件,D符合题意.
故答案为:BCD
【分析】利用已知条件结合零点存在性定理、奇函数的定义、奇函数和偶函数的定义判断函数奇偶性的方法、充分条件、必要条件的判断方法,进而找出说法正确的选项。
11.(2021高一上·靖远期末)设函数,则( )
A.当时,的值域为
B.当的单调递增区间为时,
C.当时,函数有2个零点
D.当时,关于x的方程有3个实数解
【答案】A,B,D
【考点】函数的值域;函数单调性的性质;根的存在性及根的个数判断;函数的零点
【解析】【解答】对A,当时,若x>1,,若x≤1,,于是的值域为,A符合题意;
的单调递增区间是和,因为的单调递增区间是,所以,即,B符合题意;
当时,由,得,当时,令,得.此方程有唯一解,得,即,C不符合题意;
当时,如图所示,
的图象与直线有3个交点,D符合题意.
故答案为:ABD.
【分析】由a的取值即可得出函数的解析式,然后由指数函数和二次函数的性质即可求出函数的值域,由此判断出选项A正确;结合指数函数和二次函数的单调性即可得出函数的单调性,由此即可求出a的取值范围,由此判断出选项B正确;由零点和方程根的关系即可求出a的取值范围,由此即可判断出选项C错误;利用数形结合法即可求出,当时 方程解的个数,由此即可判断出选项D正确,从而即可得出答案。
12.(2022·莆田模拟)已知定义在上的函数( )
A.若恰有两个零点,则的取值范围是
B.若恰有两个零点,则的取值范围是
C.若的最大值为,则的取值个数最多为2
D.若的最大值为,则的取值个数最多为3
【答案】A,C
【考点】三角函数的最值;函数零点的判定定理
【解析】【解答】令,
若恰有两个零点,则有:,
解得的取值范围是:,
若的最大值为,分两种情况讨论:
①当,即时,根据正弦函数的单调性可知,,
解得:
②当,即时,根据正弦函数的单调性可知,在上单调递增
则有:,
结合函数与在上的图象可知,如下图:
故存在唯一的,使得,
综上可知,若的最大值为,则的取值个数最多为2。
故答案为:AC
【分析】令,若恰有两个零点结合零点存在性定理,得出实数的取值范围,若的最大值为,再利用分类讨论的方法,①当,得出时,再根据正弦函数的单调性求出函数的最大值,进而求出的值;②当,得出时,再根据正弦函数的单调性可知函数在上的单调性,进而求出函数得知最大值,即,再结合函数与在上的图象可知,得出存在唯一的,使得,进而得出若的最大值为时的实数的取值最多的个数,从而找出正确的选项。
三、填空题
13.若二次函数 的两个零点分别是2和3,则 的值为 .
【答案】-4
【考点】一元二次方程的解集及其根与系数的关系;函数的零点与方程根的关系
【解析】【解答】因为二次函数 的两个零点分别是2和3,
所以一元二次方程 的两个根分别是2和3,
由一元二次方程根与系数关系得: ,解得 ,
因此, 。
故答案为:-4。
【分析】利用函数的零点与方程的根的等价关系,因为二次函数 的两个零点分别是2和3,所以一元二次方程 的两个根分别是2和3,再利用韦达定理求出a,b的值,从而求出2a+b的值。
14.(2020高一上·沈阳期末)已知函数 则不等式 的解集是 .
【答案】{x|x≤1}
【考点】分段函数的应用
【解析】【解答】∵函数 ,
∴当x-1≥0,即 时, ,故 ;
当 ,即 时, ,故 ;
∴不等式 的解集是:{x|x≤1}.
故答案为:{x|x≤1}.
【分析】分x-1≥0和两种情况代入对应的解析式求解,即可求得不等式 的解集。
15.(2020高一上·天津期末)若f(x)= 是定义在R上的减函数,则a的取值范围是 .
【答案】
【考点】函数单调性的性质;分段函数的应用
【解析】【解答】由题意知, ,
解得 ,所以 .
故答案为:
【分析】由题意结合一次函数的单调性:一次项系数大于零为增函数,一次项系数小于零为减函数;即可得到关于a的不等式组求解出a的取值范围即可。
16.(2021高二下·湖北开学考)已知函数 (其中e为无理数且 )在 上有两个零点,且 使 成立,则实数a的取值范围为 .
【答案】 且
【考点】利用导数研究函数的单调性;函数的零点与方程根的关系
【解析】【解答】由函数 在 上有两个零点,即方程 在 上有两个解,
即方程 在 上有不等于2的根,
令 ,则 ,
所以函数 在 上为单调递增函数,
所以 且 ,
又由 使 成立,即 使得 成立,
即 使 ,即 使 成立,
函数 在 上为单调递增函数,所以 ,
综上可知,实数a的取值范围为 且 。
故答案为: 且 。
【分析】由函数 在 上有两个零点,再结合函数的零点与方程的根的等价关系,即方程 在 上有两个解,即方程 在 上有不等于2的根,令 ,再利用求导的方法判断函数的单调性,所以函数 在 上为单调递增函数,所以 且 ,又由 使 成立,即 使得 成立,即 使 成立,再利用函数 在 上的单调性,所以 ,从而求出实数a的取值范围。
四、解答题
17.(2020高一上·吉林期末)某沙漠原来面积为 ,经过绿化改造,每年沙漠面积的减少率为 ,当沙漠面积到原来面积的一半时,所用时间是 年,已知到2020年年末,沙漠剩余面积为原来面积的
(1)求
(2)到2020年年末,该沙漠已改造了多少年?
【答案】(1)解:由题意,可得 ,整理得 .
(2)解:设经过 年剩余面积为原来的 ,可得 ,
所以 ,
由(1)知 ,即 ,可得 ,解得 .
答:到2020年年末,该沙漠已改造了5年.
【考点】函数模型的选择与应用
【解析】【分析】(1)利用已知条件建立函数模型,从而求出p的值。
(2)利用已知条件建立函数模型,再利用(1)的结论结合指数幂的运算法则,从而求出到2020年年末,该沙漠已改造了的年数。
18.(2020高三上·兴宁期末)小明在某物流派送公司找到了一份派送员的工作,该公司给出了两种日薪薪酬方案.甲方案:底薪100元,每派送一单奖励1元;乙方案:底薪140元,每日前54单没有奖励,超过54单的部分每单奖励20元.
(1)请分别求出甲、乙两种薪酬方案中日薪y(单位:元)与送货单数n的函数关系式;
(2)根据该公司所有派送员100天的派送记录,发现派送员的日平均派送单数满足以下条件:在这100天中的派送量指标满足如图所示的直方图,其中当某天的派送量指标在 时,日平均派送量为 单.若将频率视为概率,回答下列问题:
①估计这100天中的派送量指标的平均数(同一组中的数据用该组区间的中点值作代表) ;
②根据以上数据,设每名派送员的日薪为 (单位:元),试分别求出甲、乙两种方案的日薪 的分布列及数学期望. 请利用数学期望帮助小明分析他选择哪种薪酬方案比较合适?并说明你的理由.
【答案】(1)解:甲: ,乙: ,故为
,
(2)解:①读图可知,20个0.1,30个0.3,20个0.5,20个0.7,10个0.9,故平均数
②甲:
P(概率) 0.2 0.3 0.2 0.2 0.1
X(日薪) 152 154 156 158 160
EX=
乙:
P(概率) 0.2 0.3 0.2 0.2 0.1
X(日薪) 140 140 180 220 260
EX=
乙的期望更高,故答案为:择乙方案.
【考点】根据实际问题选择函数类型
【解析】【分析】(1)根据题意,列出解析式即可;
(2) ① 分别计算出每个区间中点值的个数,然后乘以总数,求和,除以个数,即可得到平均值 ② 分别计算出每个指标下薪资待遇,计算期望,比较大小做出选择。
19.(2021·河北模拟)已知函数 .
(1)从① ,② 这两个条件中选择一个,求 零点的个数;
(2)若 ,讨论函数 的单调性.
注:若第(1)问选择两个条件分别解答,则按第一个解答计分.
【答案】(1)选①,当 时, , ,
令 ,
则 ,所以 在 上是单调递增函数,
设 为 的根,
由 , ,
所以 ,
当 时 , 单调递减,
当 时 , 单调递增,
所以 在 处有最小值, ,且 ,
所以 ,
因为 ,所以 ,
因为 , ,
此时 有2个零点;
选②,当 时, , ,
令 ,
则 ,所以 在 上是单调递增函数,
在 上是单调递减函数,
在 有最大值 ,所以 , 是单调递增函数,
因为 , ,
所以 , 在 单调且连续,所以存在 使得 ,
即零点的个数为1.
(2)若 , ,令 ,
所以 ,
令 ,得 或 ,
当 时,
(i) 时, , 单调递增,
(ii) 时, , 单调递减,
(iii) 时, , 单调递增,
当 时,
由 时, , 单调递增,
当 时,
(i) 或 时, , 单调递增,
(ii) 时, , 单调递减.
【考点】利用导数研究函数的单调性;函数零点的判定定理
【解析】【分析】 (1)若选①:求出f(x), h(x)= f' (x),利用导数判断h (x )的单调性,结合函数零点的存在性定理,即可判断f (x )零点的个数;
若选②:求出f(x),令h(x)= f' (x),利用导数判断h (x )的单调性,结合函数零点的存在性定理,即可判断f (x )零点的个数;
(2)令函数g(x)= xf(x),求出g' (x)= 0的根,分 , , 三种情况,判断导函数的正负,从而得到函数的单调性.
20.(2021高一上·青岛期中)某科研单位在研发某种合金产品的过程中发现了一种新型合金材料,由大数据分析得到该产品的性能指标值y(y值越大产品性能越好)与这种新型合金材料的含量x(单位:克)的关系:当 时,y是x的二次函数;当 时, .测得的部分数据如下表所示:
x 0 2 4 12 …
y -4 4 4 …
(1)求y关于x的函数解析式;
(2)求该新型合金材料的含量x为何值时产品性能达到最佳.
【答案】(1)当 时,y是x的二次函数,设 ,
由 , 可得 ,
由 , 可得 ①,
由 , 可得 ②,
由①②得 , ,
即
当 时, ,
由 , ,可得 ,即
综上,
(2)1°当 时, ,
所以当 时,y取得最大值5
2°当 时, 单调递减,所以当 时,y取得最大值4
综上所述,当该新型合金材料的含量为3时产品性能达到最佳.
【考点】函数解析式的求解及常用方法;分段函数的解析式求法及其图象的作法;函数的最值及其几何意义;分段函数的应用
【解析】【分析】(1)根据题意由特殊值代入法计算出a与b的值,从而得到函数的解析式。
(2)由已知条件把实际问题转化为数学问题,结合题意由二次函数和指数函数的性质即可求出函数的最值。
21.(2021·嘉定模拟)数学建模小组检测到相距3米的A,B两光源的强度分别为a,b,异于A,B的线段 上任意一点C处的光强度y等于两光源到该处的强度之和,设 米.
(1)假设某处的光强度与光源的强度成正比,与到光源的距离的平方成反比,比例系数为常数 ,测得数据:当 时, ;当 时, ,求A,B两处的光强度,并写出函数 的解析式;
(2)假设某处的光强度与光源的强度成正比,与到光源的距离成反比,比例系数为常数 ,测得数据:当 时, ;当 时, ,问何处的光强度最弱?并求最弱处的光强度.
【答案】(1)解:由已知,得
所以 , ,故 ,
(2)解:由已知,得 ,所以 ,
故 , .
因为 ,
当且仅当
所以当 时的C处,光强度最弱为
【考点】基本不等式在最值问题中的应用;函数模型的选择与应用
【解析】【分析】(1) 由已知,得 ,再利用当 时, ;当 时, ,从而结合代入法解方程组求出a,b的值,进而求出函数的解析式。
(2) 由已知,得 ,再利用当 时, ;当 时, ,从而结合代入法解方程组求出a,b的值,进而求出函数的解析式为 , ,
因为 ,再结合均值不等式求最值的方法,从而求出当 时的C处,光强度最弱为 。
22.(2021高一上·深圳竞赛)将连续正整数1,2,……,n (n∈N*)从小到大排列构成一个数123……*n,F(n)为这个数的位数(如n=12时,此数为123456 789 101 112,共有15个数字,F(12)=15),现从这个数中随机取一个数字,p(n)为恰好取到0的概率.
(1)求p(100);
(2)令g(n)为这个数中数字0的个数,f(n)为这个数中数字9的个数,h(n)= f(n)-g(n),S={n|h(n)=1,n≤100,n∈N*},求当n∈S时p(n)的最大值.
【答案】(1)解:当 n=100时,这个数中总共有192个数字,其中数字0的个数为11,所以恰好取到0的概率为p(100)= -
(2)当n=b(1≤b≤9,b∈N), g(n)=0;
当n=10k+b(1≤k≤9, 0≤b≤9, k∈N*, b∈N)时,g(n)=k;
当n=100时,g(n)=11, 即g(n)=
同理有f(n)=
由h(n)= f(n)-g(n)=1,可知n=9,19, 29,39, 49,59,69, 79,89,90,
所以当n≤100时,S={9,19, 29,39,49,59,69, 79,89,90}.
当n=9时,P(9)=0
当n=90时,p(90)=
当n=10k+9(1≤k≤8,k∈N*)时,p(n)=
由y= 关于k单调递增,故当n=10k+9(1≤k≤8, k∈N *)时,p(n)的最大值为p(89)=
又 <
所以当n∈S时,p(n)的最大为 -
【考点】分段函数的解析式求法及其图象的作法;古典概型及其概率计算公式;分段函数的应用
【解析】【分析】(1)根据古典概型概率计算公式求解即可;
(2)根据分段函数的定义,结合题意分别求得函数g(n),f(n),再根据h(n)= f(n)-g(n)=1,结合古典概型概率计算公式,利用分类讨论思想求解即可.
18
