沪科版数学七年级下册 10.3 平行线的性质 课件(共27张PPT)
文档属性
| 名称 | 沪科版数学七年级下册 10.3 平行线的性质 课件(共27张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 909.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-18 16:37:38 | ||
图片预览





文档简介
(共27张PPT)
10.3.1 平行线的性质
一、温故知新
两直线平行
1、同位角相等
2、内错角相等
3、同旁内角互补
平行线的判定方法是什么?
反过来,如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢
知识生成
学习目标
1、掌握平行线的三个性质。
2、经历平行线的性质的探索过程,会用平行线
的性质 解决有关的计算和推理。
3、经过对比,理解平行线的性质和判定的区别。
重点:平行线的性质和应用。
难点:平行线的性质和判定的区分以及应用
它们进行有关推理。
1、带着目标自学课本
2、同桌交流自学中的疑惑
3、组内交流收获(数学组长负责叫讲解)
如图,
(1)∵ a ∥ b (已知)
∴ ∠1__∠2 ( )
(2)∵ a ∥ b (已知)
∴ ∠2____∠3 ( )
(3)∵ a ∥ b (已知)
∴ ∠2+∠4=____ ( )
=
两直线平行,同位角相等
=
两直线平行,内错角相等
180 °
两直线平行,同旁内角互补
c
a
b
1
2
3
4
预习效果检测
心动 不如行动
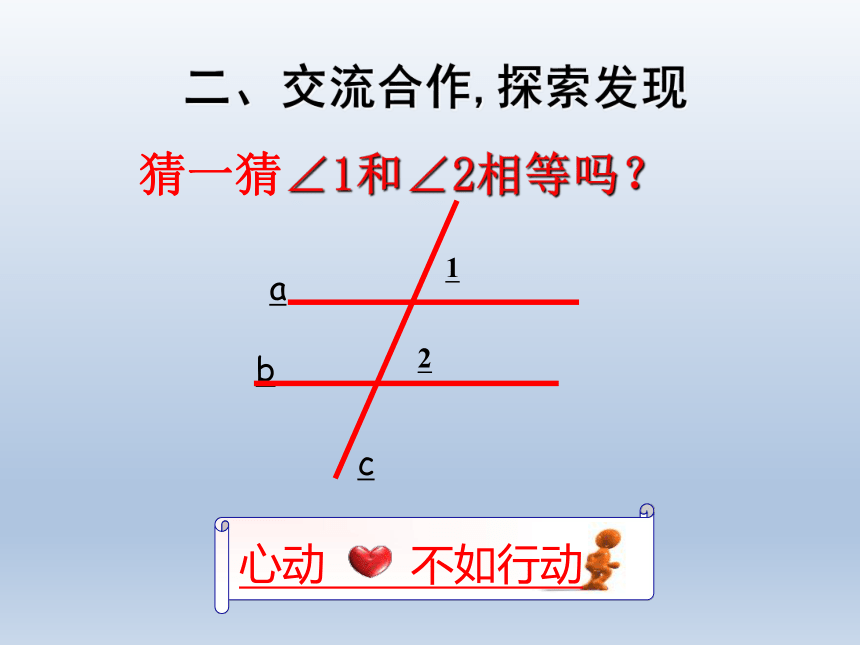
猜一猜∠1和∠2相等吗?
b
1
2
a
c
二、交流合作,探索发现
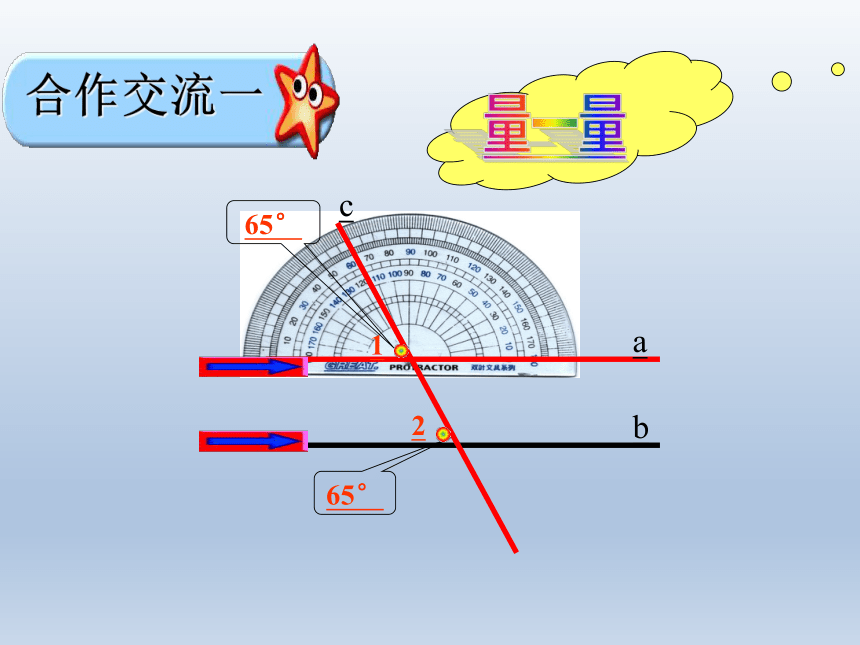
65°
65°
c
a
b
1
2
合作交流一
b
2
a
c
1
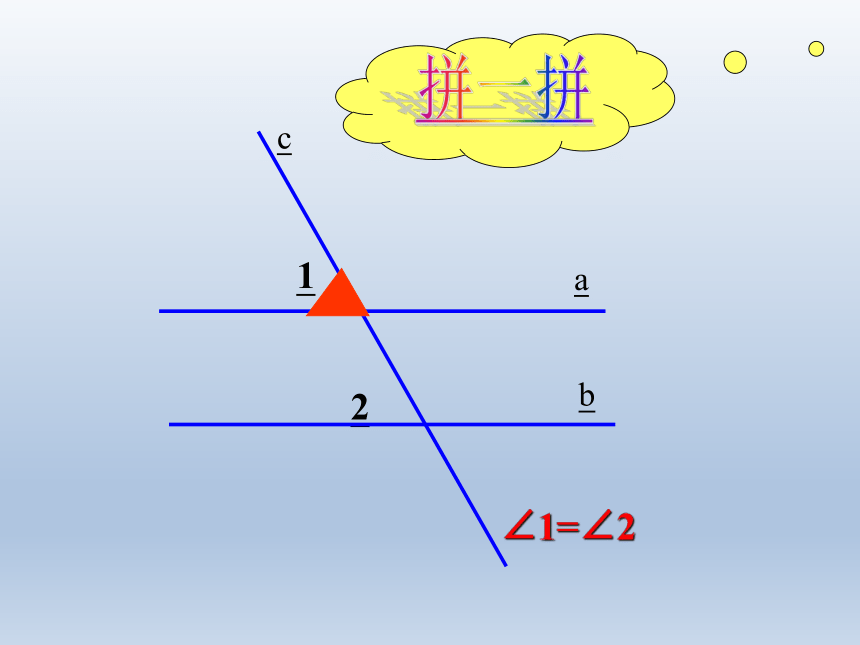
∠1=∠2
是不是任意一条直线去截平行线a、b
所得的同位角都相等呢?
两直线平行,同位角相等.
平行线的性质1
结论
两条平行线被第三条直线所截,
同位角相等.
性质发现
∴∠1=∠2.
∵a∥b,
简写为:
符号语言:
b
1
2
a
c
如图:已知a//b,那么 2与 3相等吗?
为什么
解∵a∥b(已知),
∴∠1=∠2(两直线平行,
同位角相等).
又∵ ∠1=∠3(对顶角相等),
∴ ∠2=∠3(等量代换).
合作交流二
b
1
2
a
c
3
两直线平行,内错角相等.
平行线的性质2
结论
两条平行线被第三条直线所截,
内错角相等.
性质发现
∴∠2=∠3.
∵a∥b,
符号语言:
简写为:
b
1
2
a
c
3
解: ∵a//b (已知),
如图,已知a//b,那么 2与 4有什么关系呢?为什么
合作交流三
b
1
2
a
c
4
∴ 1= 2(两直线平行, 同位角相等).
∵ 1+ 4=180° (邻补角定义),
∴ 2+ 4=180° (等量代换).
两直线平行,同旁内角互补.
平行线的性质3
结论
两条平行线被第三条直线所截,
同旁内角互补.
性质发现
∴ 2+ 4=180°.
∵a∥b,
符号语言:
简写为:
b
1
2
a
c
4
例 如图,已知直线a∥b,
∠1 = 500, 求∠2的度数.
a
b
c
1
2
∴∠ 2= 500 (等量代换).
解:∵ a∥b(已知),
∴∠ 1= ∠ 2
(两直线平行,内错角相等).
又∵∠ 1 = 500 (已知),
变式1:已知条件不变,求∠3,∠4的度数?
3
4
三、师生互动,典例示范
变式2:已知∠3 =∠4,∠1=47°,求∠2的度数?
∴∠ 2= 470
( )
解:∵ ∠3 =∠4( )
∴a∥b
( )
又∵∠ 1 = 470 ( )
c
1
2
3
4
a
b
d
如图在四边形ABCD中,已知AB∥CD,
∠B = 600.
①求∠C的度数;
②由已知条件能否求得∠A的度数
A
B
C
D
解: ① ∵ AB∥CD(已知),
∴ ∠B + ∠C= 1800(两直线平行,同旁内角互补).
又∵ ∠B = 600 (已知),
∴∠C = 1200 (等式的性质).
②根据题目的已知条件,
无法求出∠A的度数.
四、能力提升
D
C
E
F
A
A
G
G
1
2
小明在纸上画了一个角∠A,准备用量角器测量它的度数时,因不小心将纸片撕破,只剩下如图的一部分,如果不能延长DC、FE的话,你能帮他设计出多少种方法可以测出∠A的度数?
世界著名的意大利比萨斜塔,建于公元1173年,为8层圆柱形建筑,全部用白色大理石砌成塔高54.5米.
1
它与地面所
成的较大的
角是多少度
95
0
目前,它与地面所成的较小的角
为∠1=85
2
3
结论
平行线的性质1(公理)
两条平行线被第三条直线所截,同位角相等。
简单说成:两直线平行,同位角相等。
平行线的性质:
性质1:两直线平行,同位角相等.
性质2:两直线平行,内错角相等.
性质3:两直线平行,同旁内角互补.
平行线的“判定”与“性质”有什么不同
比一比
已知角之间的关系(相等或互补),得到两直线平行
的结论是平行线的判定。
已知两直线平行,得到角之间的关系(相等或互补)
的结论是平行线的性质。
同位角相等
内错角相等
同旁内角互补
两直线平行
判定
性质
已知
得到
得到
已知
小结:
1、如图,已知平行线AB、CD被直线AE所截
(1)从 ∠1=110o可以知道∠2 是多少度 为什么?
(2)从∠1=110o可以知道 ∠3是多少度?为什么?
(3)从 ∠1=110 o可以知道∠4 是多少度?为什么?
当堂检查
一、快速抢答
2
E
1
3
4
A
B
D
C
∠2=110o
∵两直线行,内错角相等
∠3=110o
∵两直线平行,同位角相等
∠4=70o
∵两直线平行,同旁内角互补
一、当堂检查
2、如图,一条公路两次拐弯前后两条路互相平行。第一次拐的角∠B是142゜,第二次 拐的角∠C是多少度?为什么?
B
C
∠C=142o
∵两直线平行,内错角相等
两直线平行
同位角相等
内错角相等
同旁内角互补
线的关系
角的关系
判定
性质
平行线的性质和平行线的判定方法的 区 别 与 联 系
小结
10.3.1 平行线的性质
一、温故知新
两直线平行
1、同位角相等
2、内错角相等
3、同旁内角互补
平行线的判定方法是什么?
反过来,如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢
知识生成
学习目标
1、掌握平行线的三个性质。
2、经历平行线的性质的探索过程,会用平行线
的性质 解决有关的计算和推理。
3、经过对比,理解平行线的性质和判定的区别。
重点:平行线的性质和应用。
难点:平行线的性质和判定的区分以及应用
它们进行有关推理。
1、带着目标自学课本
2、同桌交流自学中的疑惑
3、组内交流收获(数学组长负责叫讲解)
如图,
(1)∵ a ∥ b (已知)
∴ ∠1__∠2 ( )
(2)∵ a ∥ b (已知)
∴ ∠2____∠3 ( )
(3)∵ a ∥ b (已知)
∴ ∠2+∠4=____ ( )
=
两直线平行,同位角相等
=
两直线平行,内错角相等
180 °
两直线平行,同旁内角互补
c
a
b
1
2
3
4
预习效果检测
心动 不如行动
猜一猜∠1和∠2相等吗?
b
1
2
a
c
二、交流合作,探索发现
65°
65°
c
a
b
1
2
合作交流一
b
2
a
c
1
∠1=∠2
是不是任意一条直线去截平行线a、b
所得的同位角都相等呢?
两直线平行,同位角相等.
平行线的性质1
结论
两条平行线被第三条直线所截,
同位角相等.
性质发现
∴∠1=∠2.
∵a∥b,
简写为:
符号语言:
b
1
2
a
c
如图:已知a//b,那么 2与 3相等吗?
为什么
解∵a∥b(已知),
∴∠1=∠2(两直线平行,
同位角相等).
又∵ ∠1=∠3(对顶角相等),
∴ ∠2=∠3(等量代换).
合作交流二
b
1
2
a
c
3
两直线平行,内错角相等.
平行线的性质2
结论
两条平行线被第三条直线所截,
内错角相等.
性质发现
∴∠2=∠3.
∵a∥b,
符号语言:
简写为:
b
1
2
a
c
3
解: ∵a//b (已知),
如图,已知a//b,那么 2与 4有什么关系呢?为什么
合作交流三
b
1
2
a
c
4
∴ 1= 2(两直线平行, 同位角相等).
∵ 1+ 4=180° (邻补角定义),
∴ 2+ 4=180° (等量代换).
两直线平行,同旁内角互补.
平行线的性质3
结论
两条平行线被第三条直线所截,
同旁内角互补.
性质发现
∴ 2+ 4=180°.
∵a∥b,
符号语言:
简写为:
b
1
2
a
c
4
例 如图,已知直线a∥b,
∠1 = 500, 求∠2的度数.
a
b
c
1
2
∴∠ 2= 500 (等量代换).
解:∵ a∥b(已知),
∴∠ 1= ∠ 2
(两直线平行,内错角相等).
又∵∠ 1 = 500 (已知),
变式1:已知条件不变,求∠3,∠4的度数?
3
4
三、师生互动,典例示范
变式2:已知∠3 =∠4,∠1=47°,求∠2的度数?
∴∠ 2= 470
( )
解:∵ ∠3 =∠4( )
∴a∥b
( )
又∵∠ 1 = 470 ( )
c
1
2
3
4
a
b
d
如图在四边形ABCD中,已知AB∥CD,
∠B = 600.
①求∠C的度数;
②由已知条件能否求得∠A的度数
A
B
C
D
解: ① ∵ AB∥CD(已知),
∴ ∠B + ∠C= 1800(两直线平行,同旁内角互补).
又∵ ∠B = 600 (已知),
∴∠C = 1200 (等式的性质).
②根据题目的已知条件,
无法求出∠A的度数.
四、能力提升
D
C
E
F
A
A
G
G
1
2
小明在纸上画了一个角∠A,准备用量角器测量它的度数时,因不小心将纸片撕破,只剩下如图的一部分,如果不能延长DC、FE的话,你能帮他设计出多少种方法可以测出∠A的度数?
世界著名的意大利比萨斜塔,建于公元1173年,为8层圆柱形建筑,全部用白色大理石砌成塔高54.5米.
1
它与地面所
成的较大的
角是多少度
95
0
目前,它与地面所成的较小的角
为∠1=85
2
3
结论
平行线的性质1(公理)
两条平行线被第三条直线所截,同位角相等。
简单说成:两直线平行,同位角相等。
平行线的性质:
性质1:两直线平行,同位角相等.
性质2:两直线平行,内错角相等.
性质3:两直线平行,同旁内角互补.
平行线的“判定”与“性质”有什么不同
比一比
已知角之间的关系(相等或互补),得到两直线平行
的结论是平行线的判定。
已知两直线平行,得到角之间的关系(相等或互补)
的结论是平行线的性质。
同位角相等
内错角相等
同旁内角互补
两直线平行
判定
性质
已知
得到
得到
已知
小结:
1、如图,已知平行线AB、CD被直线AE所截
(1)从 ∠1=110o可以知道∠2 是多少度 为什么?
(2)从∠1=110o可以知道 ∠3是多少度?为什么?
(3)从 ∠1=110 o可以知道∠4 是多少度?为什么?
当堂检查
一、快速抢答
2
E
1
3
4
A
B
D
C
∠2=110o
∵两直线行,内错角相等
∠3=110o
∵两直线平行,同位角相等
∠4=70o
∵两直线平行,同旁内角互补
一、当堂检查
2、如图,一条公路两次拐弯前后两条路互相平行。第一次拐的角∠B是142゜,第二次 拐的角∠C是多少度?为什么?
B
C
∠C=142o
∵两直线平行,内错角相等
两直线平行
同位角相等
内错角相等
同旁内角互补
线的关系
角的关系
判定
性质
平行线的性质和平行线的判定方法的 区 别 与 联 系
小结
